以生为本 智慧引思——以苏教版二年级下册“有余数的除法”教学为例

江苏东台市实验小学（224200）　陈松兰

以生为本智慧引思——以苏教版二年级下册“有余数的除法”教学为例

江苏东台市实验小学（224200）陈松兰

作为课堂教学的引导者，教师要智慧地处理“让学”与“引思”的关系，教师要适时“引”、有效“引”、智慧“引”，课堂才会真正实现以生为本。

引思知识生长点思维断层处智慧碰撞处

《义务教育数学课程标准（2011）版》指出，学生的学习应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动。高效的数学课堂中，教师应做学生学习的引导者，做学生学习的引路人，智慧引思，促学生发展。

一、引思，“引”在知识生长点

“好的学习，不是来自教师找到了一种好的教学方法，而是来自给学生更好的机会去建构。”教师要立足学生学情，以学生已有的知识和观念作为新知识教学的起点，顺着学生的知识生长点，“引”学生独立思考。

【课例1】“分数的意义”教学片断

师：这块饼能换成一个西瓜吗？能换成一个苹果吗？……所以这块饼代表的是什么？（一个物体）

师生共同小结，得出单位“1”：

这里，教师精心设计研究素材，激发学生已有的知识经验，为学生对新知识的深入研究奠定基础；立足学生学习的最近发展区，通过连续追问的三个问题，在知识生长点处适时“引”，使学生的思维走向实质，学生对单位“1”的理解也逐步走向深入，对概念的认识也进一步清晰、深化。

二、引思，“引”在思维断层处

心理特点决定了学生的思维具有一定局限性，学生对知识的理解往往呈现片面性、定式性、呆板性。教师应全面分析了解学生和教材，在学生思维断层处“引”思，拓展学生的认知，弥补学生的不足。

【课例2】“商不变的规律”教学片断

1.课件出示：计算下面各题，你有什么发现？

（54×2）÷（18×2）=

（54×3）÷（18×3）=

（54×5）÷（18×5）=

（54÷6）÷（18÷6）=

（54÷9）÷（18÷9）=

（54÷18）÷（18÷18）=

我的发现＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

2.小组交流自己的计算及发现。

3.全班交流汇报。

（学生自由汇报结果，教师适时引导）

师：大家发现的这个规律是不是只适用于“54÷18”呢？我们要确定这个规律，还需要干什么？

生：需要进一步验证其他算式是否也存在这样的规律。

师：谁能举几个例子进行验证？

（学生举例，教师板书）

师：（54×0）÷（18×0）和（54÷0）÷（18÷0）这两个例子行吗？难道前面的规律错了？

（学生讨论交流，得出完整的商不变的规律）

在学生思维断层处，教师顺势“引”思：“老师也来举两个例子”，适时将“0”这一特殊情况纳入，丰富了学生的探索空间，引导学生改变思维方式，让探索更全面，更完善，更深刻。

三、引思，“引”在智慧碰撞处

引思的目的，是为了促进学生的发展。课堂教学中，不同学生对知识的理解处于不同层次，有的清晰，有的模糊；有的真实有效，有的也许徒劳无益。教师应抓住问题的本质，准确“引”思，既让不同的学生经历思维，体验学习的乐趣，也不让课堂教学航向走偏，真正发挥教师的主导作用。

【课例3】“分数的意义”教学片断

课件出示图示：

图1　

师：如图1，第1行四个饼看作单位“1”，第二行用哪个数表示？第三行呢？第四行呢？

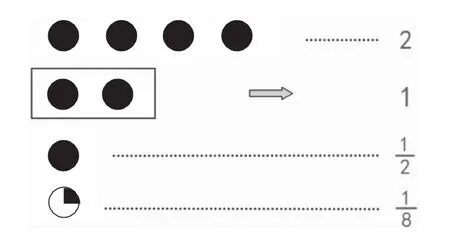
图2　

师：如图2，第2行的两个饼看作单位“1”，第一行用哪个数表示？第三行呢？第四行呢？

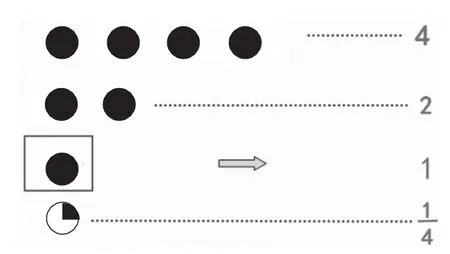
图3　

师：如图3，第三行的1个饼看作单位“1”，第一行用哪个数表示？第二行呢？第四行？

图4　

师：如图4，刚刚的三种情况放在一起，什么是不变的？（饼的数量）什么是变化的？（单位“1”）

这里，教师为学生提供了开放的、极具挑战性的平台，让学生的思考有方向，思维更完整。

作为课堂教学的引导者，教师要智慧地处理“让学”与“引思”的关系，教师要适时“引”、有效“引”、智慧“引”，这样的课堂才会真正实现以生为本的目标。

（责编金铃）

G623.5

A

1007-9068（2016）29-006