一种基于全站仪的飞机惯导参数原位检测方法

2016-11-11邓乐武,舒武静

新技术新工艺 2016年8期

通过在飞机机场测定高精度基准点和基准线，利用徕卡全站仪高精度测量能力及可编程性，建立机场区域惯性基准坐标系，分别观测基准点和飞机姿态标志点获取相应的点之间的距离、角度和坐标，并经开发的专用软件计算后获得飞机精确的位置、姿态和航向等信息。同时，利用惯导系统检测仪监测到惯导系统对准完后输出的位置、航向和姿态角等参数，得到飞机工作输出的惯导参数。二者数据进行直接比对，实现飞机在任意停机状态时惯导参数的原位检测。

惯导；全站仪；原位检测；坐标转换

惯性导航系统是一种自主工作，并为飞机上其他系统，如雷达、飞行控制系统和任务计算机等提供航向、姿态和位置等相关信息的系统。它提供的相关信息直接影响飞机空中飞行和作战品质的优劣。惯性导航系统虽然能自主性导航，由于导航误差随时间积累，因此对其输出的参数精度要求高；而且惯性导航系统通过安装支架安装在飞机上，它的初始安装误差也会严重影响惯性导航系统的导航精度。所以，飞机惯导参数的准确性检测是必不可少的。

传统的惯导部件标定和飞机惯性导航系统安装误差参数的标定都依赖于建立水平面，而航向测定依赖于磁航向，不能满足惯导真航向参数的检测[1-3]。原位检测技术是在惯性导航部件处于飞机安装状态时进行的。汪洋等利用坐标变换及方位角、俯仰角的计算，研究了船载分系统的安装精度要求[4]。戴邵武等对导弹捷联惯导系统原位标定技术进行了研究[5]。本文研究的方法是基于全站仪高精度测量及可编程性，建立统一坐标系，能在飞机任意停机状态下对惯导系统参数进行检查，减少了飞机架水平的过程。

1 原位检测原理

原位检测是指惯性导航系统通过安装支架安装在飞机上后，飞机不需要进行水平调整(即惯性导航部件处于飞行器安装状态)的情况下进行检测的方法。

在机场内建立基准塔标，塔标顶部安放反射棱镜，利用天文大地测量获得塔标一等高精度点位地理坐标值，选取两塔标连线作为真航向基准线。通过全站仪对已知基准目标和被测飞机目标的照准观测，来获取相应的点之间的距离、水平角、竖直角和坐标等，经专用软件解算出飞机的航向、姿态及位置数据，存入数据存储卡或通过数据线传递至外场检测仪。飞机原位上电，在惯导对准转导航工作模式后，可通过外场检测仪得到惯导系统实际输出的惯导参数，将全站仪数据与外场检测仪数据进行对比分析，从而得到检测结果。

1.1 航向角检测原理

在已知双目标情况下，首先在飞行器上安装代表飞机纵轴的2个位置目标反射棱镜，在地面用全站仪分别照准观测2个已知目标后，再照准观测代表飞机纵轴的2个标志点目标反射棱镜，获得相应的距离、竖直角和水平角，然后解算出飞机的航向角。各点在水平面上的投影位置关系如图1所示，航向基准线即两塔标连线的真航向基准线，A′B′为已知目标，F′T′为被测飞机目标。

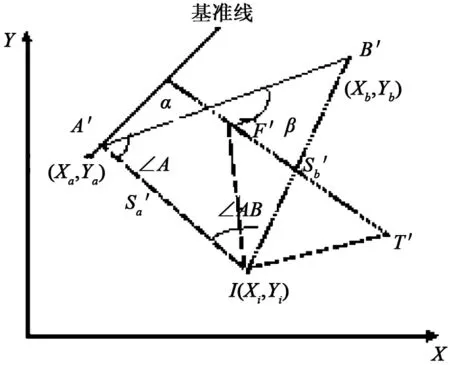
图1 各点在水平面上的投影位置关系图

已知A′(Xa，Ya)、B′(Xb，Yb)、F′(Xf，Yf)、T′(Xt，Yt)各点坐标，全站仪可测得I与A、B、F、T之间的距离和竖直角。图1中A′B′与代表飞机纵轴的F′T′之间的夹角为β，若A′B′与基准线夹角为θ，则代表飞机纵轴的F′T′的方位角φ如下：

(1)

解算出F′T′的方位角，即得到航向角。

1.2 姿态检测原理

快速测量飞机的倾斜角和俯仰角，在代表飞机横轴或纵轴的标志点上分别粘贴2片专用反射目标棱镜，在调整好全站仪电子水平后，先后观测代表飞机横轴或纵轴的反射目标棱镜，得到相应的距离、竖直角和水平角等，然后进行解算。仪器与姿态标志点的位置关系如图2所示，CD为被测飞机目标。

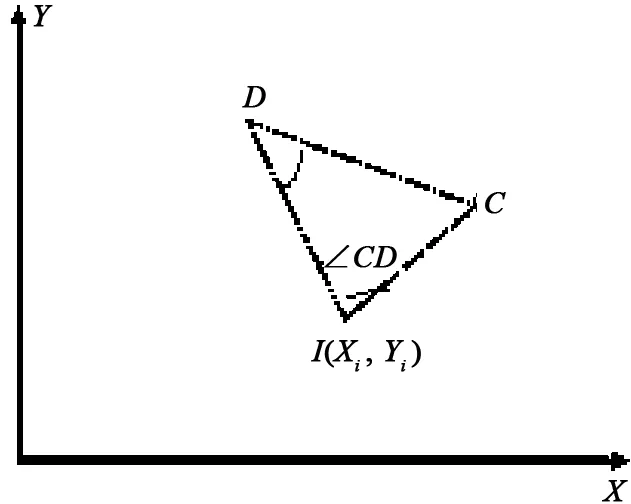
图2 仪器与姿态标志点的位置关系图

全站仪测得I与C、D之间的距离Sc、Sd和竖直角α1、α2，IC与ID之间的夹角即水平角∠CD。若两点不倾斜，则Scsinα1=Sdsinα2；若存在倾斜，可根据式2和式3求出倾斜角γ。

(2)

(3)

式中，Sc d为C、D之间的距离。

同理，可求出俯仰角(此处略去)。

2 基于全站仪的四目标前方交会原位测量方法

全站仪作为一种集光学、机电为一体的精密测量仪器具备目标跟踪测量的能力。它可以输出水平角、垂直角和斜距等测量信息，实现目标的空间三维定位。四目标前方交会原位测量方法是全站仪分别照准观测已知目标，再照准观测未知目标，通过点位移植法，由已知目标进行坐标移植得到未知目标坐标，并解算出方位角的方法。

该方法具体包括数据测量与数据解算等2个部分。基于徕卡全站仪的可编程性，建立统一坐标系，将数据测量与数据解算制成专用软件并植入全站仪内，实现四目标前方交会，即可解算出飞机精确的位置、姿态和航向等信息。

2.1 数据测量

全站仪调整水平，观测已知基桩A、B的棱镜，将其精确对中、整平，即可测量出A、B在其测量坐标系下的坐标(Xa，Ya，Ha)、(Xb，Yb，Hb)。通过角度测量和距离测量可解算出两已知点之间的距离。利用型号工程天文大地测量已知点A、B之间的标准距离Sab来进行测量精度的检核，以保证后续测量解算出的航向、倾斜角和俯仰角误差均≤0.01°，满足惯导系统原位功能、性能检查的要求。

点A、B之间的标准距离Sab与实测值Sa、Sb及∠AB的关系如式4所示：

(4)

式中，Sa是全站仪测得I与A之间的距离；Sb是全站仪测得I与B之间的距离；∠AB是IA与IB之间的夹角。

由于测量过程中的误差或照准目标有误，会造成上述等式不成立，设其误差值为Δ，则有：

式中，M为全站仪距离测量精度。

2.2 数据解算

数据解算包括坐标的统一及点位移植，航向的解算、位置的解算与姿态的解算。

2.2.1 建立统一坐标及点位移植

全站仪建立以航向基准线即中央子午线为X轴，赤道投影方向为Y轴的统一测量坐标系，通过已知点坐标及方位角进行角度变换和坐标移植，得到未知点平面坐标。

首先，全站仪的测量进行后方交会测定观测点坐标，当设定后视点的坐标时，全站仪自动计算后视方向的方位角，并设定后视方向的水平度盘读数为其方位角。根据已知的∠A(IA′与A′B′之间的夹角)和φAB(AB与基准线之间的夹角)，即可求出AI的方位角φAI：

(5)

计算出方位角后，通过已知点坐标移植及角度变换计算观测点坐标，已知方位角φAI，即可利用式6得出I点坐标(Xi，Yi)。

(6)

然后，依次观测代表飞机纵轴的标志点，进行边角前方交会测量，测完该两坐标后由程序自动解算出飞机真航向。标志点及方位角关系如图3所示，I点坐标及AI方位角φAI已经由上述计算式求出，故I点至F点的方位角φFI满足：若φFI>90°，则φFI=∠F+φAI；若φFI<90°，则φFI=∠F+φAI-π。

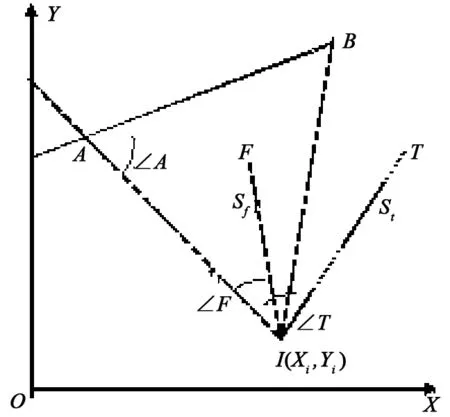
图3 标志点及方位角关系

同理，可得方位角φTI。则F(Xf，Yf)点平面坐标可由下式得出：

则T(Xt，Yt)点平面坐标可由下式得出：

2.2.2 航向及位置的解算

航向解算即解决子午线与飞机纵轴的空间异面直线关系。在已知航向基准线和F、T的平面坐标下解算出两直线的夹角，代表飞机航向的方位角φFT计算式如下：

(7)

位置解算即将平面坐标转换为大地坐标，通过迭代及高程拟合过程来实现。大地坐标系是以参考椭球面为基准面建立起来的坐标系，地面点的位置用大地经度、大地纬度和大地高度表示。高斯投影反算是将高斯坐标(X,Y)反投影计算为(B,L)的过程。当坐标投影B=φ1(X,Y)，L=φ2(X,Y)时为正形投影，X坐标轴投影成中央子午线，且X轴上的长度投影不变。设坐标反解算公式[6]如下：

(8)

式中，Bf是常数；Nf、Mf都是Bf的函数，且tf=tanBf，ηf=e2cos2Bf。

由式8可知，底点纬度Bf是一个重要的中间变量。由于投影在X轴上的长度保持不变，则当Y=0时，子午线弧长X长度保持不变，B=Bf。由赤道开始到任意纬度B平行圈之间的弧长可由积分X=C0dB求出。采用迭代法求Bf。

设Δ=cosB0(C1sinB0+C2sin3B0+C3sin5B0)，则X=C0B0-Δ，即B0=(Δ+X)/C0。

令Δ=0，则B0(0)=X/C0，代入Δ，得Δ(0)=cos(X/C0)[C1sin(X/C0)+C2sin3(X/C0)+C3sin5(X/C0)]。将Δ(0)代入B0=(Δ+X)/C0，有B0(1)=(Δ(0)+X)/C0，如此循环迭代求出Bf=B0(n)。将其代入大地坐标的计算式中，得到大地坐标(B,L)。

2.2.3 姿态的解算

快速测量飞机的倾斜角和俯仰角，在代表飞机横轴或纵轴的标志点上分别安装上目标棱镜，在调整好全站仪电子水平后，观测代表飞机横轴或纵轴的反射目标，由专用软件解算并输出倾斜角和俯仰角，计算式如下：

(9)

式中，ΔH为左右目标的高差；S为左右目标之间的斜距，其精度计算式如下：

(10)

式中，Slope(i)为每测回之倾斜角；Slope为倾斜角平均值；N为测回总数。

3 应用测试分析

结合惯性导航系统外场原位检测方法完成某型飞机的惯导参数校准过程(见图4)。首先，全站仪观测两已知位置塔标P1、P2，进行后方交会测定自身坐标；然后，全站仪观测代表飞机纵轴的飞机机上位置目标1和位置目标2进行角度前方交会测量，通过点位移植计算出目标1和目标2的坐标，测量完后解算出飞机真航向、姿态；最后，当全站仪测量解算完成后，将位置、航向和姿态等参数传输到惯性导航系统外场检测仪中。

在同样停机状态下，惯导完成对准转导航工作模式后，外场检测仪检测到惯导系统输出的位置、航向和姿态角等参数。全站仪解算结果与惯性导航系统外场检测仪测量结果对比见表1。

图4 飞机惯导参数原位检测

全站仪测量解算方位角姿态角惯导外场检测仪测量方位角姿态角误差方位角姿态角111°50'09″1°06'42″111°49'56″1°06'14″0°00'13″0°00'28″111°50'09″1°06'15″111°49'56″1°06'17″0°00'13″0°00'02″111°49'23″1°05'48″111°49'56″1°06'10″0°00'33″0°00'22″111°49'23″1°06'41″111°49'56″1°06'14″0°00'33″0°00'27″

通过验证试验可知，表1中的数据可以满足航向检查、倾斜俯仰检查0.01°的精度要求。

4 结语

采用惯性导航系统原位检测技术，在飞机正常停机状态下，不需要用千斤顶把飞机架水平即可测量多架飞机航向角、倾斜角和俯仰角，效率高，其误差均<0.01°，满足使用要求。

[1] 杨孟兴,徐兵华.激光陀螺捷联惯性导航系统的误差参数标定[J].中国惯性技术学报,2008,16(3):306-309.

[2] 武瑞娟,何红丽,惠广裕,等.基于GPS与全站仪的惯性导航部件安装校准技术[J].测控技术,2011,30(6):8-11.

[3] Zhao L, Gao W, Li P, et al. The study on transfer alignment for SINS on dynamic base[C]//International Conference on Mechatronics and Automation. Niagara: IEEE, 2005.

[4] 汪洋,赵伊宁,杜以林.船载雷达天线与航姿分系统安装精度研究[J].新技术新工艺,2015(10):66-68.

[5] 戴邵武,贺毅,徐胜红,等.舰载导弹捷联惯导系统原位标定技术研究[J].舰船电子工程,2011(9):47-49.

[6] 孔祥元,梅是义.控制测量学：下册[M].武汉:武汉大学出版社,2002.

责任编辑郑练

邓乐武，舒武静

(中航工业成都飞机工业(集团)有限责任公司，四川成都 610000)

In-situ Detection Method of INS Parameters based on Electric Total Station

DENG Lewu, SHU Wujing

(AVIC Chengdu Aircraft Industrial (Group) Co., Ltd., Chengdu 610000, China)

High precision reference points and lines are established in the airport. And using the programmability of total station, the inertial reference coordinate system can be established. Then the total station observes each reference point and aircraft attitude landmark, and acquires the data. The data is used to calculate the precise information of location, posture and course by software. Meanwhile, the corresponding output of INS is tested by inertial navigation system detector. It is compared with the former to realize situ detection of inertial parameters when a plane stops in the arbitrary condition.

inertial navigation system, total station, in-situ detection, coordinate transformation

Sab2=Sa2+Sb2-2SaSbcos∠AB

Δ=Sab2-(Sa2+Sb2-2SaSbcos∠AB)

φAI=φAB+∠A

Xi=Xa+SacosφAI

Yi=Ya+SasinφAI

Xf=Xi+SfcosφFI

Yf=Yi+SfsinφFI

Xt=Xi+StcosφTI

Yt=Yi+StsinφTI