机器学习辅助下的概率积分法参数预计模型寻优

沈　震，徐良骥，刘潇鹏，秦长才，王振兵

(安徽理工大学测绘学院，安徽 淮南 232001)



机器学习辅助下的概率积分法参数预计模型寻优

沈震，徐良骥，刘潇鹏，秦长才，王振兵

(安徽理工大学测绘学院，安徽 淮南 232001)

收集整理了多组地表移动观测站资料作为训练样本和检验样本，以工作面地质采矿条件为输入集，概率积分法预计参数为输出集，利用机器学习方法对概率积分法预测参数进行了预测。选取支持向量机、BP神经网络和偏最小二乘法3种机器学习方法对训练样本进行训练，利用训练所得模型预测检验样本中的概率积分法预测参数，并将预测结果与观测站实测值进行对比。结果表明，利用支持向量机预测下沉系数、主要影响角正切值及水平移动系数的精度最高，其平均相对误差分别达到7.46%、4.00%、13.17%;拐点偏距及开采影响传播角利用偏最小二乘法预计精度最高，平均相对误差分别为10.83%、0.88%;总体而言支持向量机的预测精度最为稳定。

概率积分法预计参数；支持向量机；BP神经网络；偏最小二乘法；模型寻优

一、预测模型及其算法简介

机器学习是指通过计算机编程实现从已知数据样本中自动分析获得规律，并利用分析结果对未知数据进行预测的方法。本文选取了机器学习中有代表性的3种方法：支持向量机、BP神经网络及偏最小二乘法对概率积分法参数进行预测。

1. 支持向量机

支持向量机，其主要思想是利用一个非线性映射K，将原本线性不可分的数据集合映射到高维空间，即

K(x,z)=φ(x)·φ(z)

(1)

式中，K为核函数；φ是从x到内积特征空间F的映射。在高维空间中选择一个超平面实现数据的最优分类，式(2)、式(3)分别为决策函数和分类平面的数学模型，利用此最优超平面对预测数据进行分类或预测[7-8]。

yi=sgn(wxi+b)

(2)

wxi+b=0

(3)

2. BP神经网络模型

BP神经网络属于按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。训练开始前计算机随机生成一组向量作为权值分配给各输入分量，随后由事先定义的决策函数F根据输入量计算得到输出数据，并根据输出结果与真实数据之间的误差反复修正权向量，直至输出结果与真实数据的中误差达到限值，最后利用网络学习所得到的模型对未知数据进行预测[8-9]。

3. 偏最小二乘法

偏最小二乘法，其通过对自变量及应变量矩阵进行主成分分解以提取其中的隐藏因子，随后通过迭代计算确定回归系数，并利用一个线性模型来描述自变量与因变量之间的关系。其数学模型如下

Y=b0+b1X1+b2X2+…+bnXn

(4)

式中，Y为因变量向量；X1、X2、…、Xn为自变量元素；b0为截距；b1、b2、…、bn为自变量元素对应的回归系数[10]。

二、样本数据训练

1. 样本数据预处理

北京大学人民医院魏来（摘要637）报告了中国3期临床研究，sofosbuvir/velpatasvir（SOF/VEL）治疗基因1～6型患者12周，耐受性好，12周总SVR为96%。不论是否有肝硬化基因1型、2型、6型均获得100%的12周SVR。基因3型12周SVR为83%（其中有16%患者为经治）。基因3b型有肝硬化的患者SVR相对低。一项来自意大利的研究显示SOF/VEL治疗基因3型12周，在代偿期肝硬化患者中的12周SVR为96.4%，在失代偿期肝硬化患者疗效欠佳。联合使用利巴韦林（RBV）未增加疗效优势。

本文以23个地表移动观测站数据作为样本，其中前19组为训练样本，后4组为检验样本。根据概率积分法预测参数、工作面地质采矿条件及机器学习方法特点，选取7个地质采矿条件参数作为样本的输入集，包括：平均开采深度H0、开采厚度m、覆岩平均坚固性系数f、松散层厚度w、采动程度n、煤层倾角α及重复采动影响。其中，采动程度n由工作面倾向长度L与平均开采深度H0的比值L/H0计算；重复采动项中0代表首采，1代表重复采动；覆岩平均坚固性系数f计算公式为

(5)

式中，mi为第i层煤层法向厚度；Ri为该层单向抗压强度。样本输入集见表1。

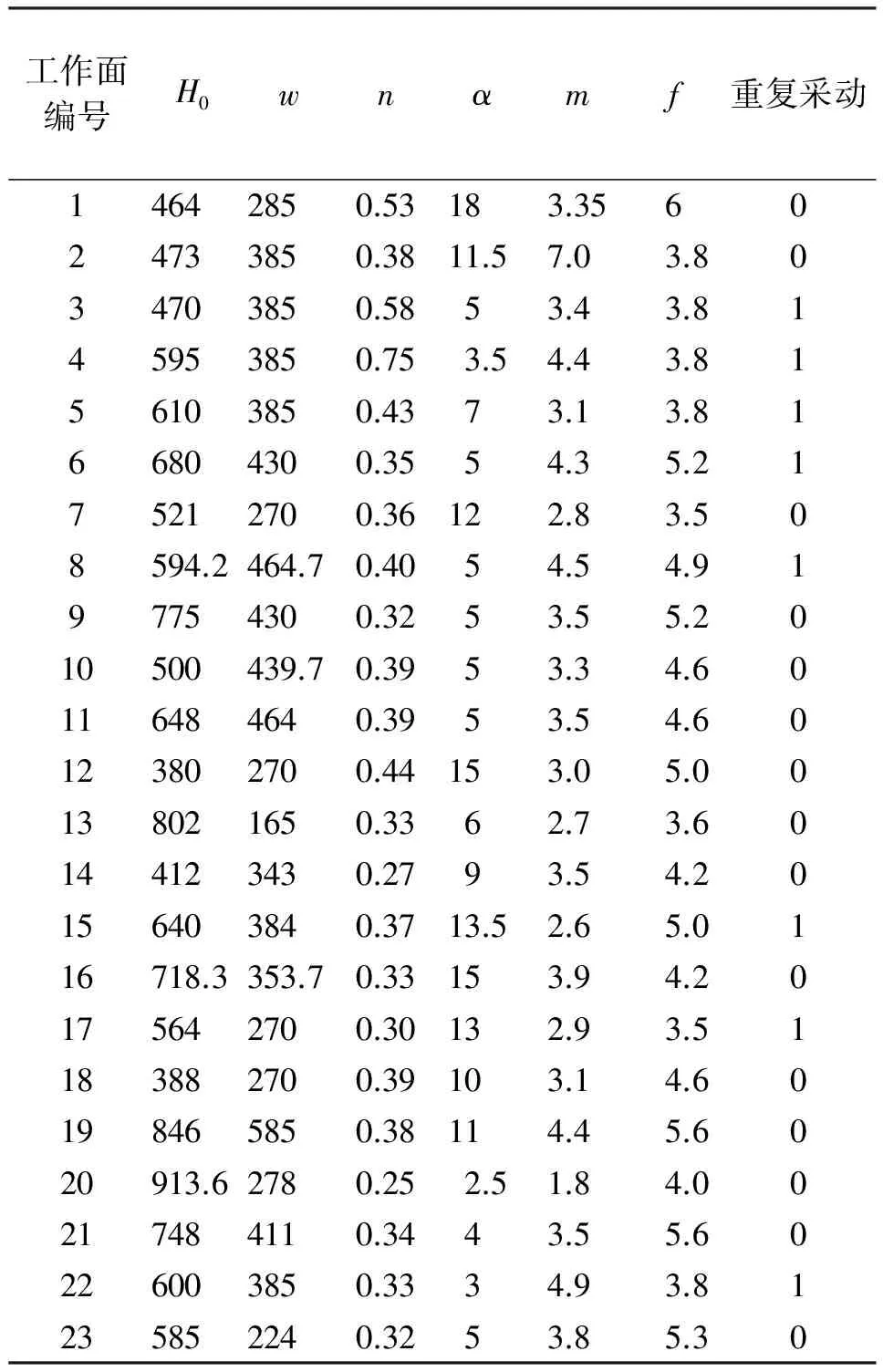
表1　工作面基本参数

输出集为概率积分法预测参数，分别为：下沉系数q、水平移动系数b、主要影响角正切值tanβ、开采影响传播角θ、拐点偏距与采深的比值S/H0，样本输出集见表2[11-12]。

表2　概率积分法预测参数

由于样本数据中包含多种参数，且参数取值范围区别较大，若直接进行训练会导致部分参数占有更大的比重，影响训练结果，因此在确定样本数据后对样本数据进行归一化处理以提高训练精度。

2. 模型训练

(1) 支持向量机训练结果

利用Matlab中的Libsvm工具箱对归一化后的样本数据进行训练，其中基础模型使用epsilon-SVR模型，核函数采用RBF(径向基)核函数，核函数gamma值设为2.8[13]。以下沉系数为例，训练结果均方误差MSE=0.035 3，图1为训练值与原始值对比图。

(2) BP神经网络训练结果

BP神经网络模型由输入层、输出层及隐藏层组成，其中输入层和输出层分别对应样本数据中的输入集和输出集。隐藏层可为一层或多层，隐藏层的节点数过少将削弱模型精度，过多会降低运算速度，本文经过试验对比将隐藏层层数设为1，节点数设置为17，神经网络模型结构如图2所示[14]。

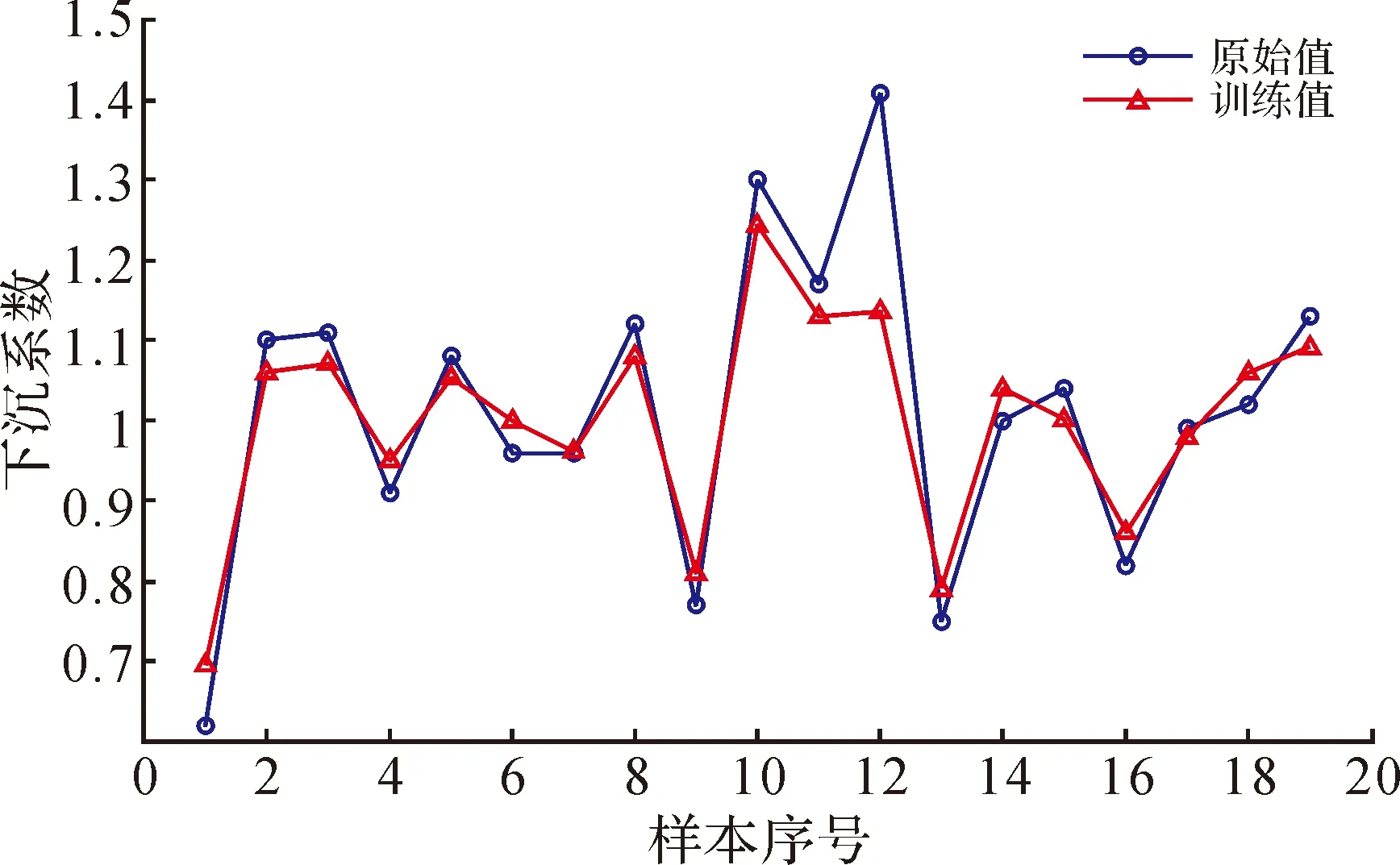
图1　支持向量机训练结果

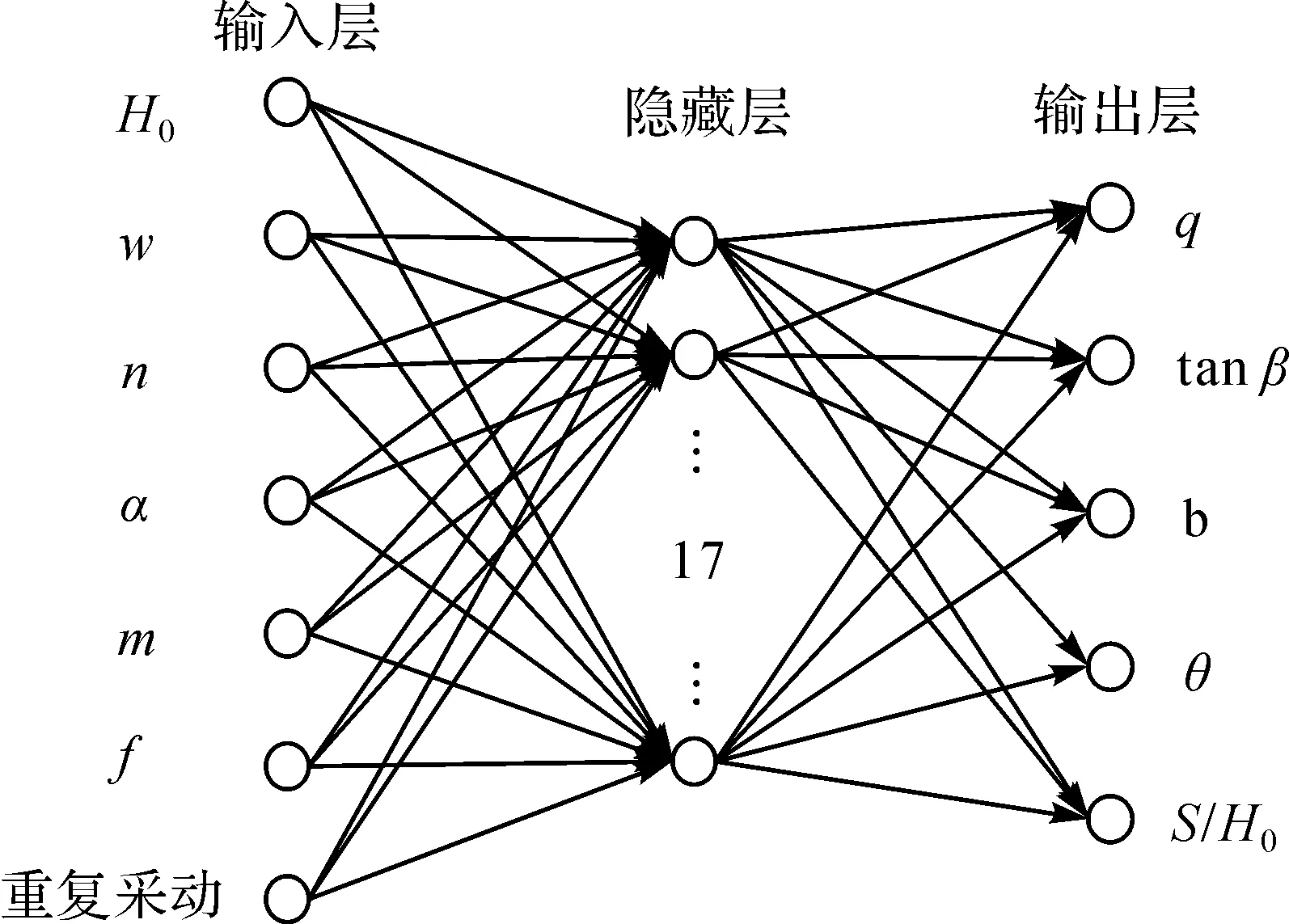
图2　BP神经网络结构

利用BP神经网络对训练样本进行训练，在9998次训练后精度趋于稳定，均方误差MSE=0.016 7。

(3) 偏最小二乘法训练结果

利用偏最小二乘法对训练样本进行训练，可得到每个因变量相对于自变量的线性模型，以下沉系数q为例，其关于工作面地质采矿条件的线性模型如下

q=1.562 3-0.000 9H0+0.001 6w-0.282 7n-0.000 3α-0.045 1m-0.077 9f-0.015 0r

(6)

训练结果与原始数据均方误差为0.011 3。

三、预测结果精度分析

利用训练所得模型对检验样本中的概率积分法参数进行预测。支持向量机、BP神经网络及偏最小二乘法预测结果见表3—表5。

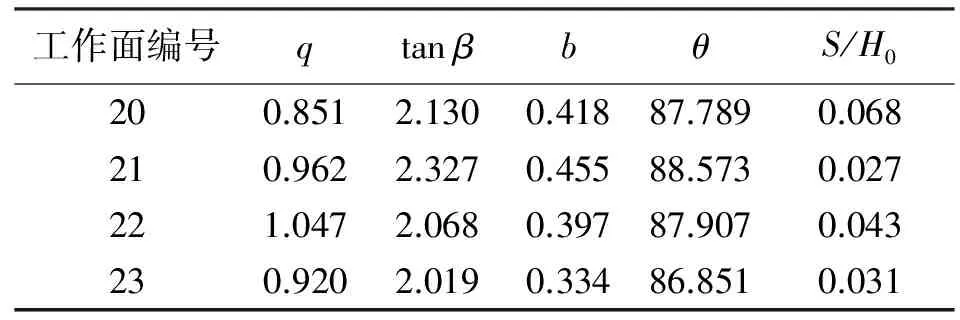
表3　支持向量机预测值

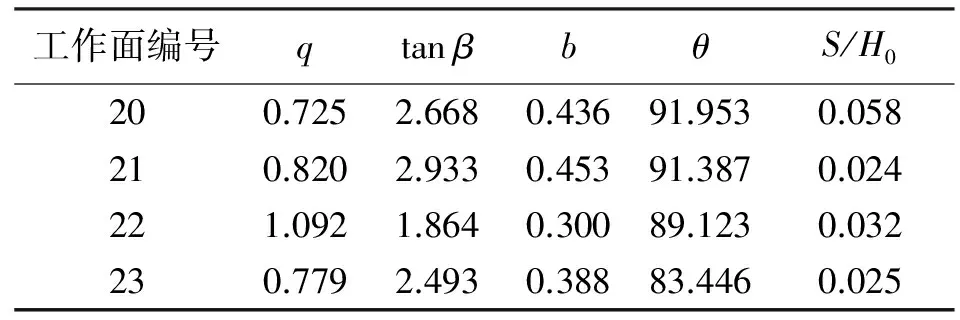
表4　神经网络预测值

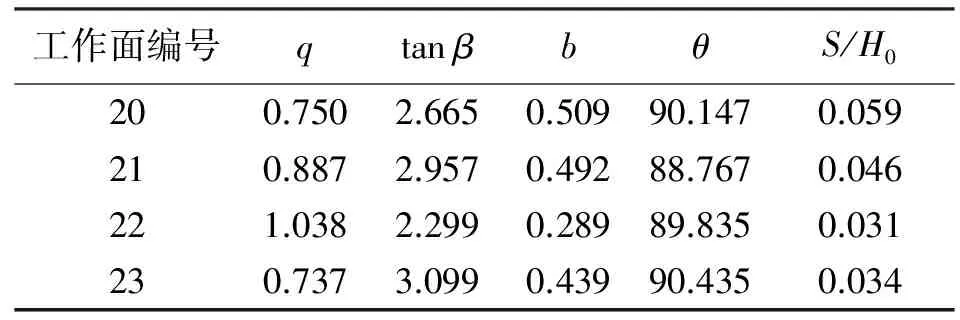
表5　偏最小二乘法预测值

将3种方法预测值与地表移动观测站解算结果进行对比，计算其平均相对误差平均值及最大相对误差，结果见表6。

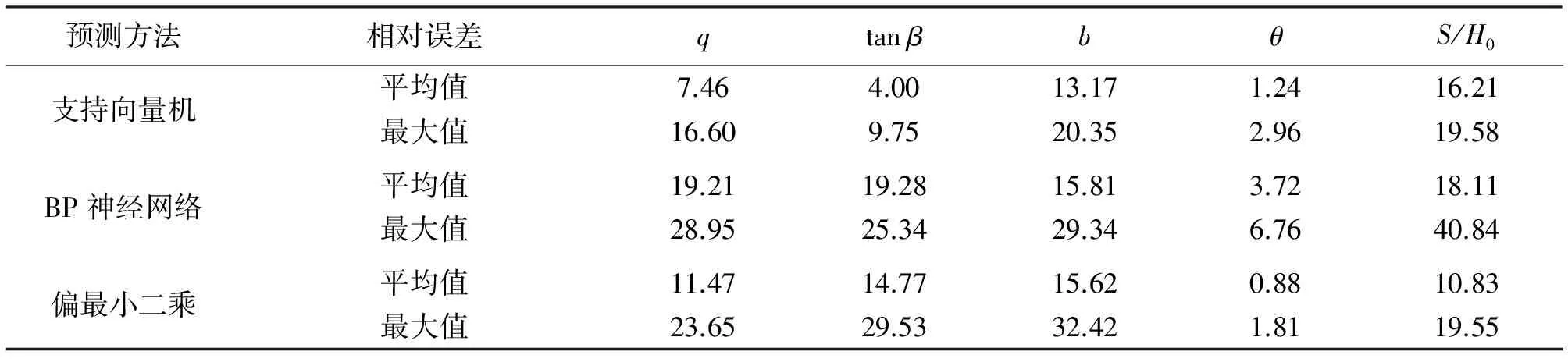
表6　预测精度对比　(%)

由表6可知，下沉系数q、主要影响角正切值tanβ及水平移动系数b利用支持向量机进行预测时精度最高；拐点偏距与采深的比值S/H0及开采影响传播角θ利用偏最小二乘法预测时精度最高；就总体预测结果而言，支持向量机的预测精度最高。

四、结　论

1) 以观测站实测数据为样本数据，采用支持向量机、BP神经网络及偏最小二乘法3种机器学习方法对概率积分法参数进行了预测，结果证明机器学习方法能够较为准确地预测概率积分法参数，为开采沉陷工作提供参考。

2) 不同的机器学习方法预测概率积分法参数时精度不尽相同，应根据实际情况选择精度最高的预测模型或多种模型结合，如利用支持向量机方法预测下沉系数q、主要影响角正切值tanβ及水平移动系数b，而拐点偏距及开采影响传播角θ则可使用偏最小二乘法进行预测。

[1]何国清,杨伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1995.

[2]邹友峰.开采沉陷预计参数的确定方法[J].焦作工学院学报(自然科学版),2001,20(4):253-257.

[3]麻凤海,杨帆.采矿地表沉陷的神经网络预测[J].中国地质灾害与防治学报,2001,12(3):87-90.

[4]郭文兵,邓喀中,邹友峰.概率积分法预计参数选取的神经网络模型[J].中国矿业大学学报,2004,33(3):88-92.

[5]杨帆，麻凤海.地表移动预计参数选取的神经网络法[J].中国地质灾害与防治学报,2004,15(1):102-106.

[6]YAN W Y, HE Q.Multi-class Fuzzy Support Vector Machine Based on Dismissing Margin[C]∥Proceedings of the Eighth International Conference on Machine Learning and Cybernetics. Baoding, China: [s.n.], 2009: 1139-1144.

[7]林卉,朱庆,胡召玲.模糊支持向量机和变化矢量分析相结合的矿区土地覆盖变化检测[J]. 测绘通报,2014(11):25-27.

[8]梁月吉,任超,杨秀发,等.结合双树复小波和广义回归神经网络的钟差预报方法研究[J].测绘通报,2016(1):6-10，18.

[9]Kerh T,Gunaratnam D,Chan Y.Neural Computing with Genetic Algorithm in Evaluating Potentially Hazardous Metropolitan Areas Result from Earthquake[J].Neural Computing & Application,2010,19(4):521-529.

[10]罗批,郭继昌,李锵,等.基于偏最小二乘回归建模的探讨[J].天津大学学报(自然科学与工程技术版),2002,35(6):783-786.

[11]徐良骥,王少华,马荣振,等.厚松散层开采条件下覆岩运动与地表移动规律研究[J].测绘通报,2015(10):52-56.

[12]刘伟韬,刘欢,陈志兴,等.地表沉陷预计参数精度分析[J].测绘科学,2016(8):1-8.

[13]范昕炜.支持向量机算法的研究及其应用[D].杭州：浙江大学,2003.

[14]刘天舒.BP神经网络的改进研究及应用[D].哈尔滨：东北农业大学,2011.

Probability Integral Method Parameters Prediction Model Optimization Based on Machine Learning Methods

SHEN Zhen，XU Liangji，LIU Xiaopeng，QIN Changcai，WANG Zhenbing

沈震，徐良骥，刘潇鹏,等.机器学习辅助下的概率积分法参数预计模型寻优[J].测绘通报，2016(10)：35-38.DOI:10.13474/j.cnki.11-2246.2016.0324.

2016-05-10

国家自然科学基金(41472323)；安徽省对外科技合作计划(1503062020)

沈震(1990—)，男，硕士生，研究方向为矿山开采沉陷。E-mail：abczhenxx@qq.com

P258

B

0494-0911(2016)10-0035-04