基于二维单基线的单星高精度无源定位算法
2016-11-11郑仕力董乔忠王笃祥
郑仕力,董乔忠,王笃祥
(中国航天科工集团8511研究所,江苏 南京 210007)
·工程应用·
基于二维单基线的单星高精度无源定位算法
郑仕力,董乔忠,王笃祥
(中国航天科工集团8511研究所,江苏 南京 210007)
针对长短基线干涉仪定位系统设备量大、系统复杂的问题,提出了基于运动学原理的单星高精度无源定位技术。以模糊相位差和相位差变化率为观测量,并采用三通道二维单基线阵列构型,充分利用长基线相位差定位精度高的特点,并结合相位差变化率的无模糊特性,通过粒子群改进算法实现高精度的定位。仿真结果表明,该算法定位精度高,定位性能接近CRLB。
二维单基线;无源定位;相位差;变化率
0 引言
电子侦察系统是一种通过截获地面、海上、空中和太空中的各类电磁辐射源辐射出来的信号,测量其信号特征参数,进而定位辐射源位置,而本身不发射信号的系统,具有无源探测安全隐蔽的优点。单星无源定位体制主要有两种:单星测向定位体制和基于运动学参数的单星定位体制。单星测向定位体制通过二维测向阵列或多波束天线来确定三维空间中辐射源射线的方向,从而确定辐射源位置。该方法能实现单次测量定位,但二维测向阵列在求解相位模糊时没有利用目标的运动参数信息,解算效率不高,多波束天线测向定位方法存在设备量和测向定位精度之间的矛盾,此外,单星测向定位中还存在对测向通道的相位一致性以及卫星载荷姿态的控制和测量精度要求较高等问题。基于运动学参数的单星定位体制通过被动接收一段时间信号的频率、到达时间和干涉仪相位差等变化信息,来确定辐射源的位置,具有定位载荷体积小、质量轻、功耗低的优点。
基于运动学参数的单星无源定位方法主要有单通道仅测频定位方法、单通道仅测多普勒频率变化率定位方法、基于旋转基线的定位方法等。本文考虑将运动学原理引入到传统的单星干涉仪定位体制中,在传统相位差干涉仪的基础上,加入相位差变化率作为观测量,提出了基于模糊相位差和相位差变化率的粒子群改进算法。该方法使用三个通道构成二维长基线,以模糊相位差和相位差变化率为观测量,充分利用长基线相位差定位精度高的特点,并结合相位差变化率的无模糊特性,通过粒子群改进算法,实现高精度的定位。有别于基于角度及其变化率的单站定位方法,本文提出的方法不需要求解相位差的模糊,而是利用模糊相位差完成对辐射源的定位。相比于其它非线性滤波算法,该算法不依赖于滤波初值的选取,能够在有效观测范围内直接确定辐射源位置。
1 定位模型与原理
如图 1所示,地面固定辐射源在地固直角坐标系下的坐标为XT=[xtyt0]T,信号频率为f,对应的波长为λ。观测平台在tn时刻的位置为Xn=[xnynzn]T。观测平台上的两条基线指向矢量为Li(t)=[li,1(t)li,2(t)li,3(t)]T,i=1,2。
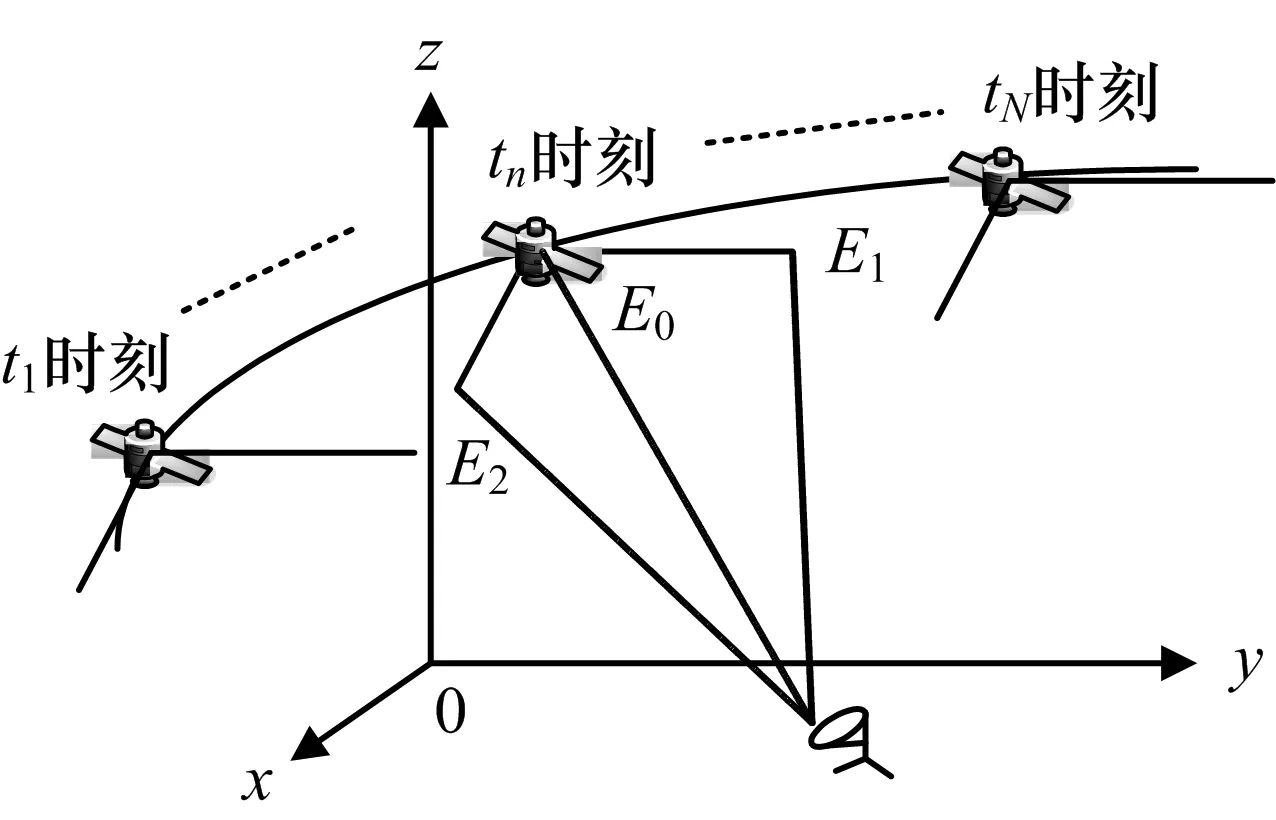
图1 定位模型示意图
(1)
(2)
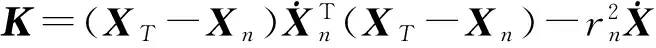
(3)
由于基线长度远大于信号波长,所以会有严重的相位模糊问题,考虑到采用传统的解模糊方法(如长短基线法等相关方法)存在设备量较大(无法在单个长基线条件下完成解模糊操作)、计算量及数据量较大等问题,本文方法充分利用观测平台与目标之间的相对运动,通过提取无模糊的相位差变化率,结合模糊相位差信息,实现单个长基线干涉仪条件下的解模糊定位。
从几何意义上不难理解,通过一次观测,单个长基线干涉仪接收到的信号相位差,对应着多个来波方向角(即测向模糊),这些方向角对应于空间的一簇定位锥面,他们与地面相交形成了一簇定位线。假定该基线经过一定时间运动到其它位置又获得一簇定位线,这两簇定位线相交得到的系列交点就对应了辐射源位置的一组模糊解。辐射源定位就是要从这组模糊位置解中确定出真实的那个位置。对于二维干涉仪,无需观测平台大范围运动,单次观测即可得到两簇相交的定位线,可大大缩短定位时间。为了进一步加快定位收敛速度,我们利用二维长基线干涉仪获取的相位差变化率信息对上述模糊的辐射源目标位置估计结果进行对标解模糊处理,即可获取无模糊的辐射源目标真实位置估计结果,系统工作原理如图 2所示。
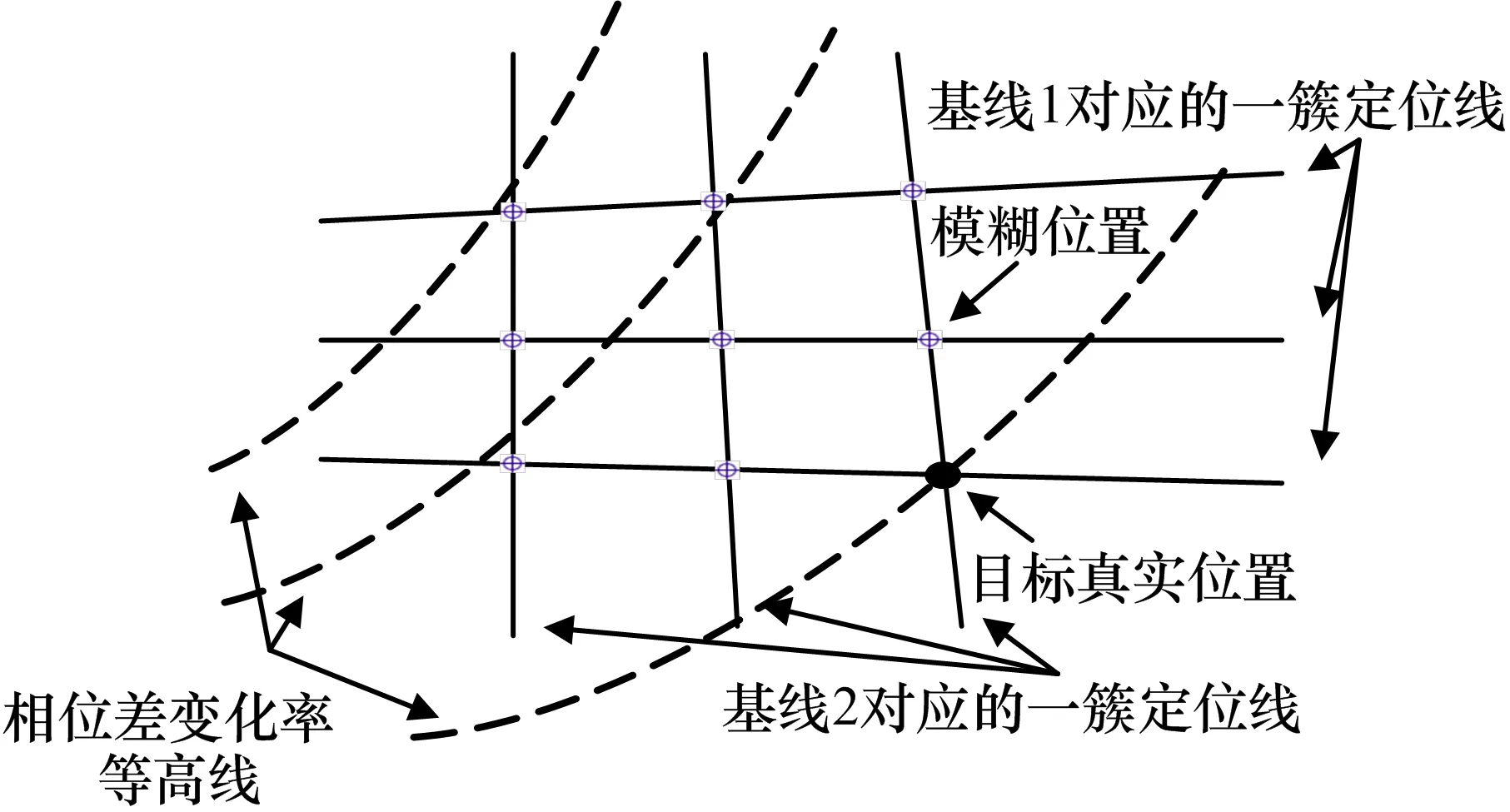
图2 定位原理示意图
理论上,这种方法可以实现快速定位。但是,当干涉仪的基线长度远大于信号波长时,相邻的模糊位置会靠得很近,相邻模糊位置对应的相位差变化率的差异会很小,甚至小于相位差变化率的测量误差,因此通过单次测量无法得到辐射源的真实位置。此时需要通过增加观测时间和观测次数,才能实现无模糊定位。
2 定位方法
本文基于运动学原理和三通道二维单基线阵列构型,充分利用目标辐射源与观测平台之间的相对运动信息,以模糊相位差和相位差变化率为观测量,并通过粒子群改进算法来获取高精度的目标位置参数估计结果。
2.1代价函数的选取
从统计意义上看,虽然每一次的测量均存在测量误差,但对于多次测量,目标真实位置是使得由该点得到的理论测量值与实际测量值最接近的位置点。假设共有N次测量,每次测量的相位差及其变化率都存在测量误差,误差符合高斯分布,则令代价函数为:
(4)
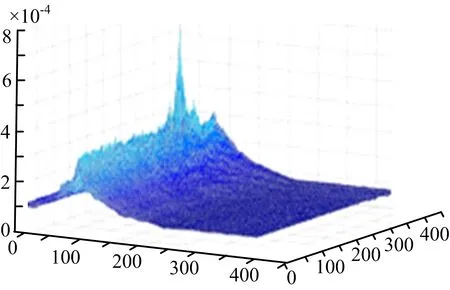
图3 由模糊相位差得到的相关函数图
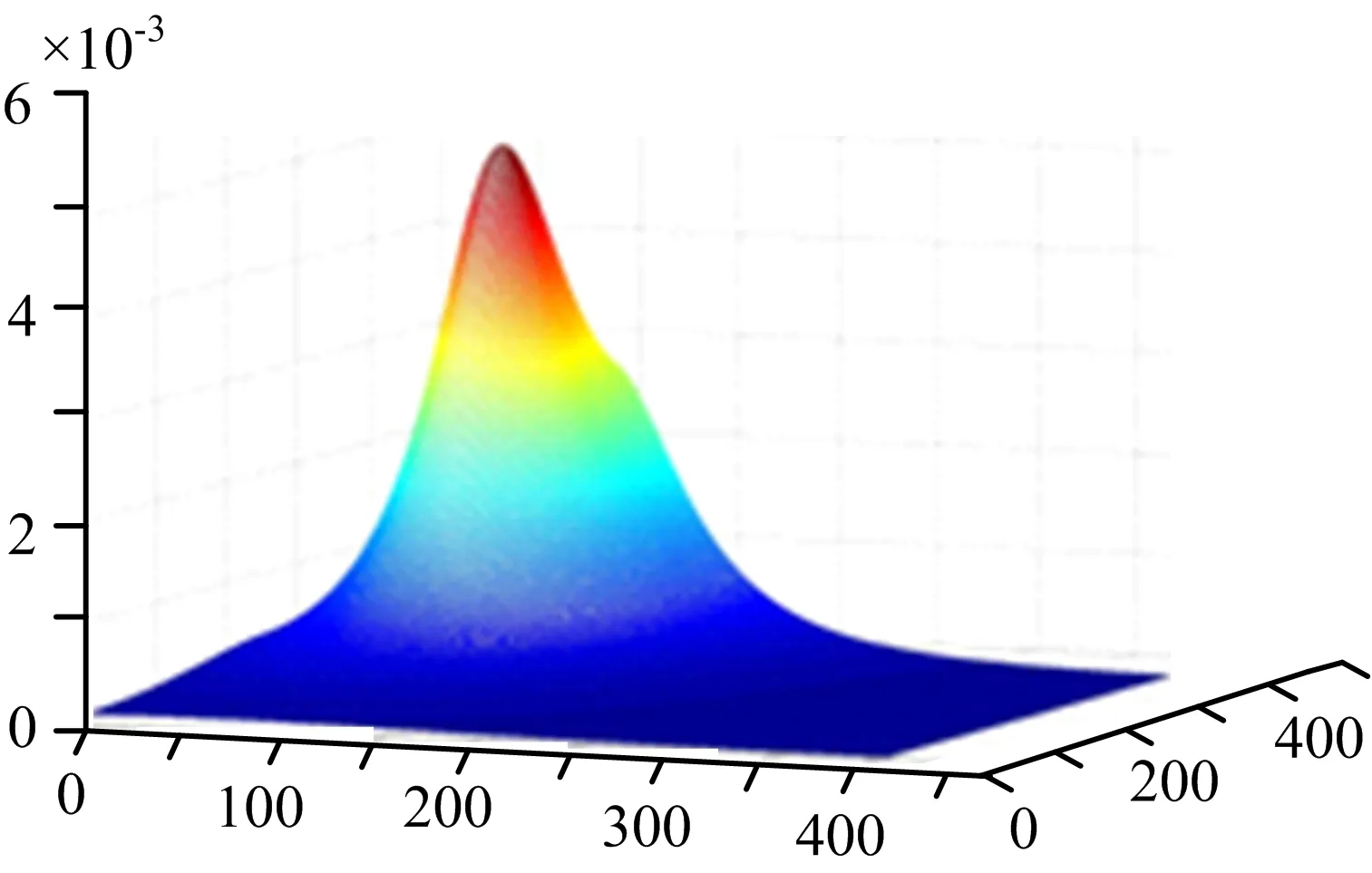
图4 由相位差变化率得到的相关函数图
由图 3、图4所示的代价函数分布情况可以发现:
1)基于模糊相位差信息的代价函数在切向和法向两个方向的分辨率,相比基于无模糊相位差变化率信息的代价函数而言更高;
2)受到模糊相位差信息影响,基于模糊相位差信息的代价函数在二维方向均存在较多模糊栅瓣,直接基于该代价函数进行辐射源目标位置参数搜索寻优,极易陷入局部最优点而导致算法失效;
3)受到基于无模糊相位差变化率信息的代价函数分辨率限制,直接基于该代价函数进行辐射源目标位置参数搜索,能够达到的辐射源目标定位精度较低。
2.2粒子群改进算法流程
针对不同类型代价函数分布特点,同时利用模糊相位差代价函数的高分辨率特性和相位差变化率代价函数的无模糊特性,规划两类代价函数的使用策略:
1)基于相位差变化率代价函数,在观测区域内大范围参数寻优,获取较低精度的辐射源目标粗定位结果,并以粗定位结果为中心,划定精定位寻优区域;
2)基于模糊相位差代价函数,在精定位寻优区域内进行参数寻优操作,获取辐射源目标高精度定位结果。精定位根据粗定位的结果缩小观测范围,有效地减小了计算量。下面给出算法的详细流程和参数设置,算法流程图如图 5所示。
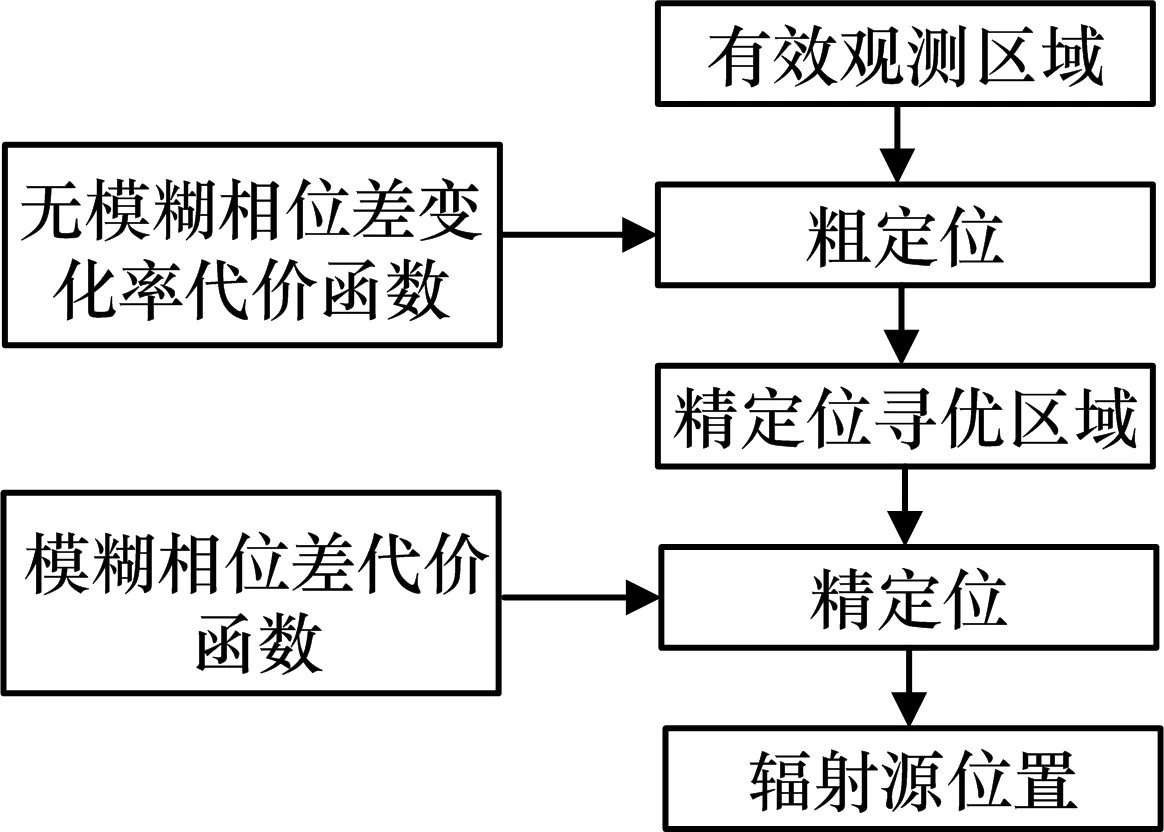
图5 粒子群改进算法流程
3 定位误差的克拉美-罗下限(CRLB)
CRLB是无偏估计所能达到的估计误差下限,根据非随机矢量估计的CRLB的定义有:
(5)
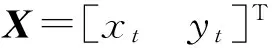
(6)
式中,φ=[φ11,φ12,…,φ1N,φ21,φ22,…,φ2N]T。根据式(1),可将式(6)进一步化简为:
(7)
(8)
(9)
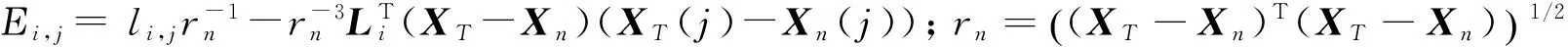
(10)
(11)
4 仿真实验结果与分析
本文采用基于相位差及其变化率的粒子群改进算法进行仿真实验,相关场景及参数经简化设置如下:
观测平台飞行高度400km,沿y轴方向匀速直线运动,速度7600m/s,初始时刻的位置是X0=[0 -100km400km]T;目标辐射源位于XT=[-50km100km0]T;搜索区域为{X(x,y,z)|-200≤x≤200,-200≤y≤200,z=0},单位是km;信号频率4GHz,二维基线长度均为10 m,相位差随机误差15°,相位差变化率随机误差30°/s。仿真统计结果如图 6所示,各表中未指明的参数均按给出的典型场景参数进行设定,定位误差都为均方根误差。
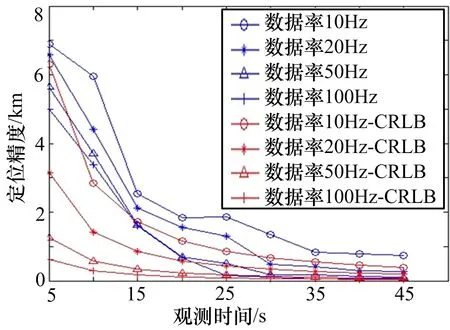
图6 不同观测时间及数据率下的定位性能
由图 6可以看出,随着观测时间的增加、数据率的增大,定位性能明显改善。当观测时间大于30s、数据率大于10Hz时,定位精度达到0.8km,定位性能接近CRLB。但是当观测时间小于15s时,受随机误差及相邻模糊点差异性过小的影响,本文提出的算法无法完全解模糊,定位精度较差。
取观测时间为30s,数据率10Hz,改变辐射源频率,得到不同频率下的定位性能,见表 1。从结果可以看出,本文提出的算法对全波段的适应性比较良好,定位性能在1.8km内。由表 1还可以看出,随着频率的提高,定位精度有所降低。这是由于随着频率的提高,波长随之减小,模糊数随之增加,更多的定位结果落在真实位置附近的模糊位置上。
取观测时间为30s,数据率10Hz,改变相位差及其变化率的随机误差,得到不同误差下的定位性能,见表 2。从结果可以看出,本文采用的方法能良好适应不同的相位差及其变化率的随机误差,在50°的随机误差范围内,定位精度均能稳定在1.7km内,受随机误差的影响较小。

表1 不同频率的定位性能
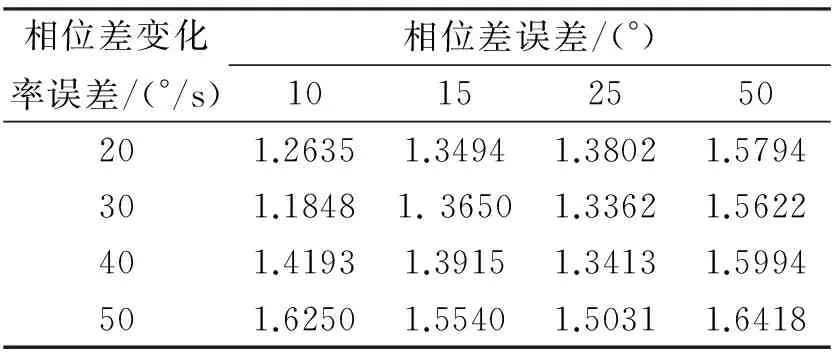
表2 不同误差的定位性能 km
5 结束语
本文以三个通道构成二维单基线,以模糊相位差和相位差变化率为观测量,利用粒子群改进算法完成了对地面固定辐射源的高精度定位。该算法充分利用长基线相位差定位精度高的特点,并结合相位差变化率的无模糊特性,具有定位收敛快、无需测向、设备量小的优点。经仿真验证,该算法在多个频段有较好的适应性,对相位差和相位差变化率的随机误差不敏感,在一定范围内均能实现高精度定位,定位性能接近CRLB。■
[1]郭福成,樊昀,周一宇,等. 空间电子侦察定位原理[M]. 北京:国防工业出版社,2012.
[2]李腾,郭福成,姜文利. 基于旋转干涉仪模糊相位差的多假设NLS定位算法[J]. 电子与信息学报,2012,34(4):956- 962.
[3]李腾,郭福成,姜文利. 星载干涉仪无源定位新方法及其误差分析[J]. 国防科技大学学报,2012,34(3):164- 170.
[4]陈曦. 基于旋转基线的单星高精度定位技术[D]. 北京:中国航天科工集团第二研究院,2012.
[5]周亚强,皇甫堪.噪扰条件下数字式多基线相位干涉仪解模糊问题[J].通信学报,2005,26(8): 16-21.
[6]龚享铱,袁俊泉,苏令华.基于相位干涉仪阵列多组解模糊的波达角估计算法研究[J].电子与信息学报,2006,28(1):55-59.
[7]李淳,廖桂生,李艳斌.改进的相关干涉仪测向处理方法[J].西安电子科技大学学报,2006,33(3):400-403.
High precision passive localization by single satellite observer using two-dimensional single baseline
Zheng Shili,Dong Qiaozhong,Wang Duxiang
(No. 8511 Research Institute of CASIC,Nanjing 210007,Jiangsu,China)
Due to the large equipment and the complex structure of multi-baseline interferometers, a new high precision passive location by single satellite observer based on particle kinematics is proposed. In view of the unambiguous specialty of the phase rate-of-changing and the high precision in direction of the long baseline phase differences, the ambiguous phase difference and the changing rate of phase difference are used in this algorithm. The particle swarm optimization algorithm is improved to accomplish the high precision passive localization. The simulation results show that this method can attain the CRLB.
two-dimensional single baseline;passive localization;phase difference;changing rate
2016-03-26;2016-05-05修回。
郑仕力(1991-),男,硕士研究生,主要研究方向为空间电子侦查、信号处理等。
TN911.7
A
