基于禁忌蝙蝠算法的支持向量机特征选择和参数优化

刘天健

基于禁忌蝙蝠算法的支持向量机特征选择和参数优化

刘天健

（广西大学计算机与电子信息学院，广西 南宁 530004）

支持向量机是一种有良好发展前景的学习机器。针对支持向量机训练过程中特征选择和参数优化的问题，提出一种基于蝙蝠算法和禁忌搜索算法相结合的算法的支持向量机特征选择和参数优化算法。将禁忌搜索算法理论引入蝙蝠算法中，可以有效提高BA算法的收敛速度和精度，得到更优的支持向量机模型。UCI标准数据集的分类实验结果表明，与基本的网格搜索，遗传算法等比较，TSBA算法可以获得更高的分类准确率和更好的稳定性。

支持向量机；蝙蝠算法；禁忌搜索算法；特征选择；参数优化

蝙蝠算法（BA）［1］是一种新的群智能优化算法。相对于其他的算法，BA算法在有效性和准确性方面有明显的提高。但是，蝙蝠算法的优化性能还不是十分完善，存在易陷入局部最优早熟收敛等问题。禁忌搜索算法（TS）作为一种智能搜索算法具有模拟人类智能的记忆机制，已被广泛应用于各类优化领域并取得了理想的效果。TS通过采用禁忌策略来限制搜索过程陷入局部最优，从而避免迂回搜索。

基于此，本文提出一种新的基于蝙蝠算法和禁忌搜索算法的混合算法TSBA算法。TSBA算法具有结合BA算法和TS算法的优点，使其具有更好的搜索能力，并且可以避免陷入局部最优，加快收敛速度，从而更好的优化SVM分类器。最后以UCI数据库案例作为本文的实验数据，对其进行仿真实验，仿真结果表明，基于禁忌蝙蝠算法优化的SVM比传统的分类算法有更高的分类精度和稳定性。

1　相关工作

1.1支持向量机原理

支持向量机［2］源于统计学理论，其思想是在n维空间中找到一个分类超平面，在这个空间建立一个最优分类超平面，将空间上的点分类。在分开的数据的超平面的两边有两个互相平行的分类超平面，最优分类超平面是多个平行超平面的距离最大值。SVM分类问题有两类：线性可分与非线性可分。线性可分问题的定义是其训练集可以用一个超平面完全正确地进行分类的问题。对于非线性的情况，SVM的处理方法是选择一个核函数，通过将数据映射到一个高维特征空间，在这个空间中构造最优分类超平面。

1.2支持向量机参数

在支持向量机中，惩罚因子值的大小代表这分类器对被误划分的点的重视程度，误差惩罚因子的值越大，表明分类器对该噪声点的重视程度越到，反之则越低。而核函数参数γ决定着样本点经映射后所在的高维特征空间区域中分布的复杂程度，核函数参数的改变意味着特征空间VC维的改变，VC维的大小决定着空间的置信范围，最终影响结构风险范围。

在SVM的众多核函数中，RBF核函数是应用最广泛的核函数之一，且因为其只有两个参数：惩罚因子C和核函数γ。所以只要能找到最优化参数组（C，γ），就能使SVM具有最好推广性。

2　混合蝙蝠算法的支持向量机参数优化

2.1混合蝙蝠算法

蝙蝠算法实现简单，但是其具有局部搜索能力弱，易陷入局部最优点，进化后期收敛速度慢等缺陷。而禁忌搜索是人工智能的一种体现，是局部搜索领域的一种扩展。禁忌搜索最重要的思想是标记对应已搜索的局部最优解的一些对象，并在进一步的迭代搜索中尽量避开这些对象（而不是绝对禁止循环），从而保证对不同的有效搜索途径的探索［3］。因此本文在基本蝙蝠算法中引入禁忌搜索思想，提高蝙蝠算法摆脱局部极值点的能力，提高基本蝙蝠算法的收敛速度和精度。

混合蝙蝠算法基本思想：

（1）采用基本的蝙蝠算法初始化相应的群体位置、速度、响度等参数，既不改变蝙蝠算法初始化时所具有的随机性本质。用第一代群体的适应度的最好值，作为当前解和全局最优解，并将其添加到禁忌表。

（2）t代第i个个体的适应度与1t-的第i个个体适应度做比较。如果t代第i个个体的优于当前全局最优解，就用禁忌搜索算法的藐视准则，把1t-代第i个个体适应度和当前全局最优解替换成t代第i个个体的适应度，并把t代第i个个体适应度加入禁忌表。

如果t代第i个个体的适应度优于1t-代第i个个体的适应度，并且不在禁忌表中，则把1t-代第i个个体的适应度替换成t代第i个个体的适应度并把该当代的适应度加入禁忌表。

如果t代第i个个体的适应度优于1t-代第i个个体的适应度，但是禁忌表中有该适应度，则忽略此次更新的速度、响度、位置等，以此来帮助蝙蝠算法跳出局部最优点，从而快速寻找到最优解。

2.2禁忌蝙蝠算法的支持向量机参数优化

本文中的SVM核函数采用的是RBF核函数，因为RBF核函数使SVM具备了线性与非线性的分类能力，并且SVM的分类能力主要受其参数核函数γ和惩罚因子C的影响。所以本文考虑核函数γ和惩罚因子C，并用该算法去优化SVM。

基于禁忌蝙蝠算法的支持向量机参数优化具体算法步骤如下：

（1）设置蝙蝠种群的规模、最大迭代次数、禁忌表的长度，搜索范围。

（2）初始化禁忌表和蝙蝠算法的相关参数值，主要包括蝙蝠种群里每只蝙蝠的音量A和脉冲速率r及其速度向量v和位置向量x，以及蝙蝠的频率f范围。

（3）初始化蝙蝠种群所有个体的位置，每一个解的位置为γ、C。

（4）评估初始代各只蝙蝠的适应度值，选出适应度值最大的个体，更新禁忌表。

（5）更新每只蝙蝠的脉冲速率、速度和位置，更新公式如下：

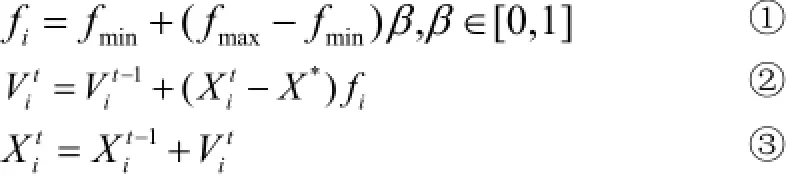
其中，β是一个从0到1的随机数；f是蝙蝠的脉冲频率，其范围根据处理的问题大小，在初始化时设定［fmin，fmax］；为种群进化t代后更新的速度，是进化t-1代后的速度；为种群进化t代后更新的位置，是进化t-1代后的位置；X*是种群中适应度最高的蝙蝠个体的位置。并且可以根据所求解的问题类型，在固定iλ（或if）的同时改变if（或iλ）。

（6）生成一个随机数rand，如果rrand＞，则对当前最优解进行一个随机的扰动，产生一个新的解后，对新解进行越界检查，如果超出范围则进行越界处理。

（8）生成一个随机数rand，如果rand＜A ，且f（）＞f），并且f（）的值不存在禁忌表中，同时将相应的对象加入禁忌表，并修改禁忌表中各对象的任期。则接受步骤（6）产生的新解，然后按如下公式对ir和iA进行更新：

（10）如未满足结束条件，则重复步骤（5）至（9）。

（11）输出全局最优解。具体流程见图1。

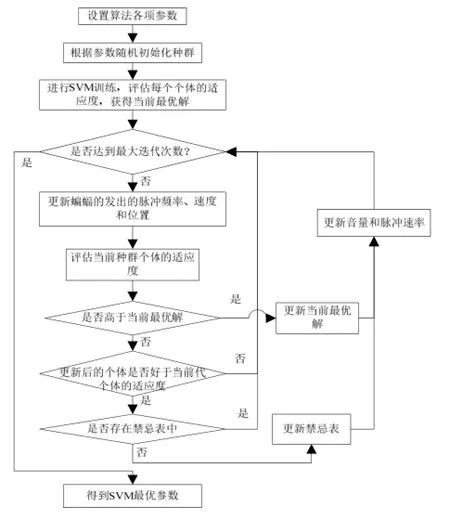
图1　TSBA-SVM的SVM参数优化流程图

3　仿真研究

3.1数据源

为了验证本文提出算法的有效性，本文采用UCI标准数据集中的7个真实的数据集，各数据集简要介绍如表1所列。

表1　来自UCI的数据集及其描述

3.2算法的参数设置

TSBA-SVM算法的参数设置：种群规模20，进化代数100，禁忌表的长度为5。

惩罚因子以及核函数参数变化范围的最小值一般是以2为底，取其幂指数的值，即，变化范围的最大值同样也是以2为底，取其幂指数的值，即

在本章的7个UCI数据集的分类测试中，惩罚因子以及核函数参数变化范围的min值皆取-5，而max皆取+5，即0.03125≤C≤32，0.03125≤r≤32。

3.3结果与分析

表2是TSBA-SVM算法与基本遗传算法和网格搜索算法的实验结果对比，按照折叠交叉确认法的K取10，对其中的若干个UCI数据集分别进行10次测试，然后去10次实验最高分类正确率的平均数。

表2　TSBA-SVM算法与GA和GS算法的性分类正确率对比

由表2的实验数据对比可见，本文算法的分类准确率都要略高于基本遗传算法［4］和网格搜索算法［5］。

从表2的实验结果来看，TSBA-SVM算法不仅分类准确率比基本遗传算法的分类准确率略高，稳定性略高于基本遗传算法；而TSBA-SVM算法不仅分类准确率比网格搜索算法的准确率更高，而且稳定性也高于网格搜索算法。说明TSBA-SVM算法不仅在分类准确率上高于GA算法和网格搜索算法，并且稳定性上有很大提升。

表3是TSBA-SVM算法与文献［6］的两种改进算法CCBSS、GS-SVM算法的实验结果对比，样本数据按照训练数据占总样本数据的50%，评价数据占25%，测试数据占25%，对于每个数据集，都分别测试30次，然后取30次实验最优分类正确率的平均值。

表3　TSBA-SVM与CCBSS和GS-SVM的分类正确率的对比

由表3的实验数据对比可见，本文算法的分类准确率相比与CCBSS、GS-SVM分别提高了5.16%、2.73%、3.12%、3.97%，并且TSBA-SVM算法在群体规模和进化代数上都要优于CCBSS、GS-SVM，由此可见TSBA-SVM算法的整体性能比CCBSS和GS-SVM算法有很大的优势。

4　结论

支持向量机的分类准确率与其参数的的选择密不可分，利用RBF核函数的优点，选取相对应的参数，能在很大程度上提高支持向量机的学习能力。本文在保留了基本蝙蝠算法所具有的随机性强、精确度高、鲁棒性好等优点的基础上，结合禁忌搜索算法的仿人工记忆的特性，提出了一种基于禁忌蝙蝠算法的支持向量机支持向量机特征选择和参数优化。TSBA-SVM可以很好的解决BA算法容易陷入局部最优、收敛速度慢的缺点。通过在7个数据集上进行实验，实验结果表明基于混合蝙蝠算法的支持向量机分类器比基本的网格搜索算法、基本遗传算法、CCBSS算法和GS-SVM算法有更高的分类准确率和更好的稳定性。

［1］ Yang X S.A new metaheuristic bat-inspired algorithm［M］// Nature inspired cooperative strategies for optimization（NICSO 2010）.Springer Berlin Heidelberg，2010：65-74.

［2］ Vapnik V N. The nature of statistical learning theory. Statistics for Engineering and Information Science［J］. Springer-Verlag，New York， 2000.

［3］ 董宗然，周慧.禁忌搜索算法评述［J］.软件工程师，2010，（2）：96-98.

［4］ Coello C A C，Montes E M. Constraint-handling in genetic algorithms through the use of dominance-based tournament selection［J］.Advanced Engineering Informatics，2002，16（3）：193-203.

［5］ Hsu C W， Chang C C， Lin C J. A practical guide to support vector classification［R］.台北：国立台湾大学资讯工程学系，2003：1-12.

［6］ 蒋华荣，郁雪.应用遗传算法优化子空间的SVM分类算法［J］.计算机科学，2013，40（11）：255-260.

Feature selection and parameter optimization for support vector machines based on Taboo bat algorithm

Support vector machine is a good development prospect of learning machine. Aiming at the problem of feature selection and parameter optimization of support vector machine in the training procedure， a novel approach based on the bat algorithm and tabu search algorithm for feature selection and parameter optimization of SVM is proposed. The tabu search algorithm theory into bat algorithm， BA can improve the convergence speed and precision to give better support vector machine model. The experimental results for UCI standard datasets show that compared with the basic GS， GA， TSBA-SVM algorithm can achieve higher classification accuracy and better stability.

Support vector machine； bat algorithms； tabu search algorithm； feature selection； parameter optimization

TP38

A

1008-1151（2016）02-0012-03

2016-01-11

刘天健（1990－），男，河北廊坊人，广西大学计算机与电子信息学院硕士生，研究方向为高性能计算与网络系统。