高中数学教学中学生错误生成的价值及纠错策略
2016-11-10江苏颜立华
◇ 江苏 颜立华
高中数学教学中学生错误生成的价值及纠错策略
◇江苏颜立华
数学是一门严谨并且对实践性要求极高的学科,需要学生不断去思考,过程中可能会犯下一些错误,教师要善于利用这些错误,给学生反省的空间,让学生在反复的实践中验证自己的观点,有意识、有目的整理自己的错误,累积经验,提高自己的准确度,避免重蹈覆辙.
1 正视错误,分析价值
学生进入高中阶段以后,知识框架与概念已经有了一个基本雏形.但是由于高中数学难度加深等一些客观原因,还有学生自身的一些主观原因,很容易犯错,因此需要学生正视自己的错误,多方面的分析错误带来的价值,这样有利于增加其学好数学的自信心.
1.1数学基础不牢固,概念不清晰
初中教材上通常将概念条框呈列出来,方便学生更好地理解与掌握,但是高中更注重培养学生自己动脑和动手的能力,需要自己不断去推理、归纳才能总结出概念,这样巨大的差距会导致刚进入高中的学生开始跟不上课程,这是高中生容易犯错的一个重要原因.

AM=N=P;BM⊆N;
CN⊆M;DN⊆P
本题从形式上看,3个集合极为相似,但深入挖掘集合的本质属性,不难发现它们是不同的集合,集合M是函数y=x2+1中x的取值范围;集合N是函数y=x2+1中y的取值范围;P是由函数y=x2+1图象上的点构成的集合.因此如对集合的概念、性质把握不准,极易出现错解.
这样的情况也给教师提供一些有价值的信息: 1)学生基础不扎实,要自己总结概念分析案例十分困难,或者是概念总结不到位,导致概念理解不清晰,在运用的过程中就容易出错. 2)教师在课堂教学过程中,没有有效地指导学生总结概念,在总结重、难点时没有做到全面.因此教师要进行反省并且思考如何改善自己的教学方案.
1.2综合性高的组合题,不能融会贯通
在复杂的高中数学学习中,犯错误是不可避免的,因为高中数学灵活性强,题型十分广泛,导致学生在课堂上所学到的不能完全满足平常的运用,而且高中数学的交会性也十分强,一道题目往往要联系多个知识点,这样也会导致学生犯错.

这道题目不仅考了椭圆的知识,又考了勾股定理的运用,是解析几何中常见的一种题型.同时也需要学生对知识点理解特别透彻才能运用自如.解题时,若未能彻底掌握此知识点或者运用不熟练,就容易出现错误.所以,这类综合性高的组合题出错的现象反映了学生融会贯通的能力还有待加强.
2 制定正确的学习方法,预防出错的指导方针
1) 扎实基础,梳理概念.
基础知识的牢固对于数学学习来说是十分重要的,教师应该从高一开始为学生巩固基本的知识,严格要求学生,通过大密度的小测试来检验学生对知识的熟悉度.要分析学生概念不清晰的根本原因,不断调整自己的教学方案,在检测学生对知识掌握情况的同时分析学生学习困难所在,然后实施相应策略.


r2=|OP|2=a2+(2a)2=5a2.
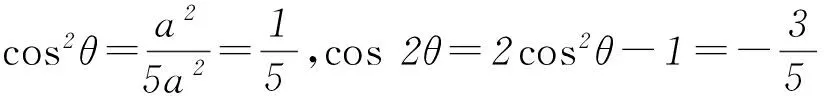
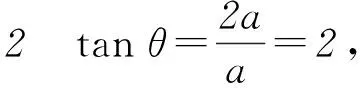
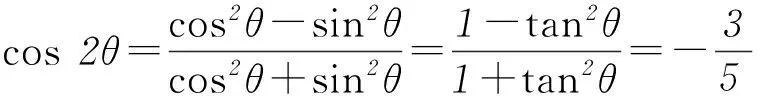
本题只要熟悉三角函数的基本定义就很容易解答出来,所以夯实基础,牢记概念十分重要.
2) 多加练习,提高正确率,增强学习信心.
教师要想让学生对数学感兴趣,就要根据学生需求的不同制定合适的教学方案,帮助学生制定最佳的学习方案,让学生自己寻找解题技巧,鼓励学生上台到黑板来演练.尽量降低教学的难度,增强学生学习的自信心.比如下面这道例题,是简单的诱导公式的套用,教师只要严格要求学生牢记诱导公式的转换与“奇变偶不变,符号看象限”的法则,即可求解.


2) 根据上面的判断方法,运用十字口诀“奇变偶不变,符号看象限”求值.
3) 由点—线—面全面梳理知识点.
高中数学与初中数学最大的区别就在于知识点更广更多,也更注重思维模式的培养.教师在讲课时更注重数学思想和方法的讲解,所以学生要学好数学,必须要将学过的知识系统分析、整理,学会举一反三.高中数学教材每个知识板块都是有关联的,教师在教学时要讲解全面.例如,学生学习了数列,在理解数列基本概念的同时,还要求学生将函数方程的思想融入其中,这对学生的数学能力要求较高,其中等差数列和等比数列是基础,仅记忆公式远远不够,比如下面例5.


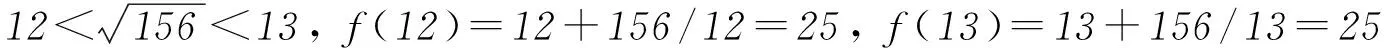
数列是特殊的函数,可从函数角度考虑,利用函数y=f(x)的性质,求数列an=f(n)的最值.
总之,高中数学教师在进行教学时要根据每个错误的不同,针对性的制定教学方案,对症下药.在发现学生问题的同时,不仅要帮助他们改正错误,更重要的是从学生错误中总结经验,善于发现错误中所蕴含的价值,才能让学生更好地掌握解答问题的技巧,提高解题正确率.
江苏省射阳中学)
