变耦型时栅传感器及测头姿态对测量误差的影响

鲁　进，陈锡侯，汤其富，武　亮

(1.重庆理工大学 电子信息与自动化学院，重庆 400054；



变耦型时栅传感器及测头姿态对测量误差的影响

鲁进1*，陈锡侯2，汤其富2，武亮2

(1.重庆理工大学 电子信息与自动化学院，重庆 400054；

2.重庆理工大学 时栅传感及先进检测技术重庆市重点实验室，重庆 400054)

根据时栅传感器的测量原理，提出一种采用高频时钟脉冲作为测量基准的变耦型时栅位移传感器以提高位移测量的精度。该传感器通过改变激励线圈和感应线圈的耦合状态输出感应位移变化的行波信号来实现精密位移测量。进行了建模和仿真，研究了不同测头姿态下传感器的位移误差特性，并对其进行了谐波分析，得到了不同测头姿态对位移测量误差各次谐波的影响规律。根据传感器模型制作了传感器并开展了验证实验。仿真和实验结果均表明：不同测头姿态对位移测量误差的影响主要体现在对测量误差的1次、2次和4次谐波上，且俯仰姿态引入的附加误差最大，其余测头姿态下引入的位移测量附加误差均较小。若保证较佳的测头姿态，传感器在定尺和动测头间气隙厚度为0.3 mm时的原始误差约为±18 μm。实验分析结果与仿真结果基本一致。

时栅传感器；位移测量；测头姿态；安装误差；测量精度

1　引　言

时栅是近几年发展起来的一种将空间位移转换成时间差，再以时钟脉冲为基准实现精确测量的位移传感器，它具有测量精度高、抗干扰能力强、智能化程度高等优点，已在大量程纳米测量和极端、特殊环境下得到有效应用[1-3]。在时栅传感器的加工和使用过程中，由于电子元器件稳定性差、温度起伏、激励电源电压波动、机械加工制造误差、机械使用过程中的变形和磨损等因素的影响，会引入测量误差，难以保证高精度位移测量的要求[4-5]。前期的研究工作主要集中在对传感器进行优化设计和对测量系统进行标定补偿，虽然能在一定条件下提高和保持测量精度[6-12]，但仍有两个问题亟待解决：其一，前期研究的自标定方法均针对角度测量，而直线位移测量系统由于难以提供类似角度测量系统中的圆周封闭的自我基准而难以实现；其二，即使实施了有效的标定补偿，当传感器系统的安装状态无法保证时，测量精度也难以保证。

针对上述问题，本文从时栅传感器测量原理出发，首先提出一种用于直线位移测量的新型变耦型时栅位移传感器，然后，通过系统的仿真分析，研究了不同测头姿态下传感器的误差特性，并通过实验进行了验证，为传感器实现高精度位移测量提供了一种新的解决方案。

2　变耦型时栅传感器的工作原理

变耦型时栅传感器由定尺和动测头两部分组成，其模型见图1。定尺由导磁材料加工而成，其上开有矩形斜槽。动测头沿测量方向上分布有两个完全相同的独立测头，测头一和测头二，并通过非导磁的联接板固定。两独立测头各自包含导磁铁芯、激励线圈和感应线圈，且激励线圈和感应线圈以多匝形式绕在各自导磁铁芯突出的4颗矩形齿上。其中，激励线圈在4颗矩形齿上依次采用正-反-反-正(绕向)的串接方式绕制，感应线圈在4颗矩形齿上依次采用正-正-反-反的串接方式绕制。

图1　时栅传感器模型

定尺和两独立测头的导磁铁芯需满足的尺寸关系见图2。图2中，W为空间极距，β为定尺斜槽角，n取正整数。n越大，两测头间的相互影响越小。

图2　定尺和两动测头的尺寸关系

当动测头沿测量方向运动时，动测头和定尺间的气隙磁导将发生变化。只考虑气隙磁导变化中的恒定分量及基波分量时，动测头两独立测头各齿下的磁导变化规律为：

(1)

(2)

式中：λ0为恒定分量；λM1为基波分量幅值；i为两独立测头各齿齿号，依次取i=1，2，3，4；k(x)为磁场耦合系数，与斜槽角β有关。若定尺斜槽角满足：

(3)

则k(x)为一常数，若β不满足式(3)，则k(x)为周期等于W/4的周期函数。式中：M为动测头宽度。

两独立测头各齿上所绕激励线圈与感应线圈间的互感抗与磁导变化规律相同，在满足式(3)时，有：

(4)

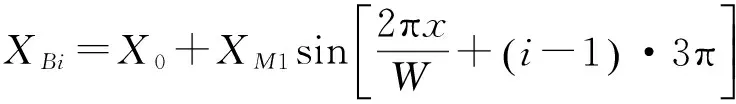
(5)

式中：X0为恒定分量；XM1为基波分量幅值。

由于激励线圈为正-反-反-正串接，感应线圈为正-正-反-反串接，故两独立测头感应线圈的输出电势分别为：

(6)

(7)

(8)

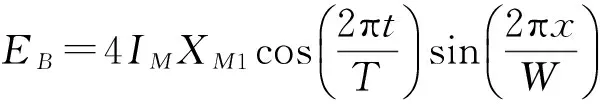
(9)

将两独立测头的感应线圈串联，即可得到位移测量所需的信号：

E=EA+EB=

(10)

后续电路对传感器输出信号的处理过程如图3所示。

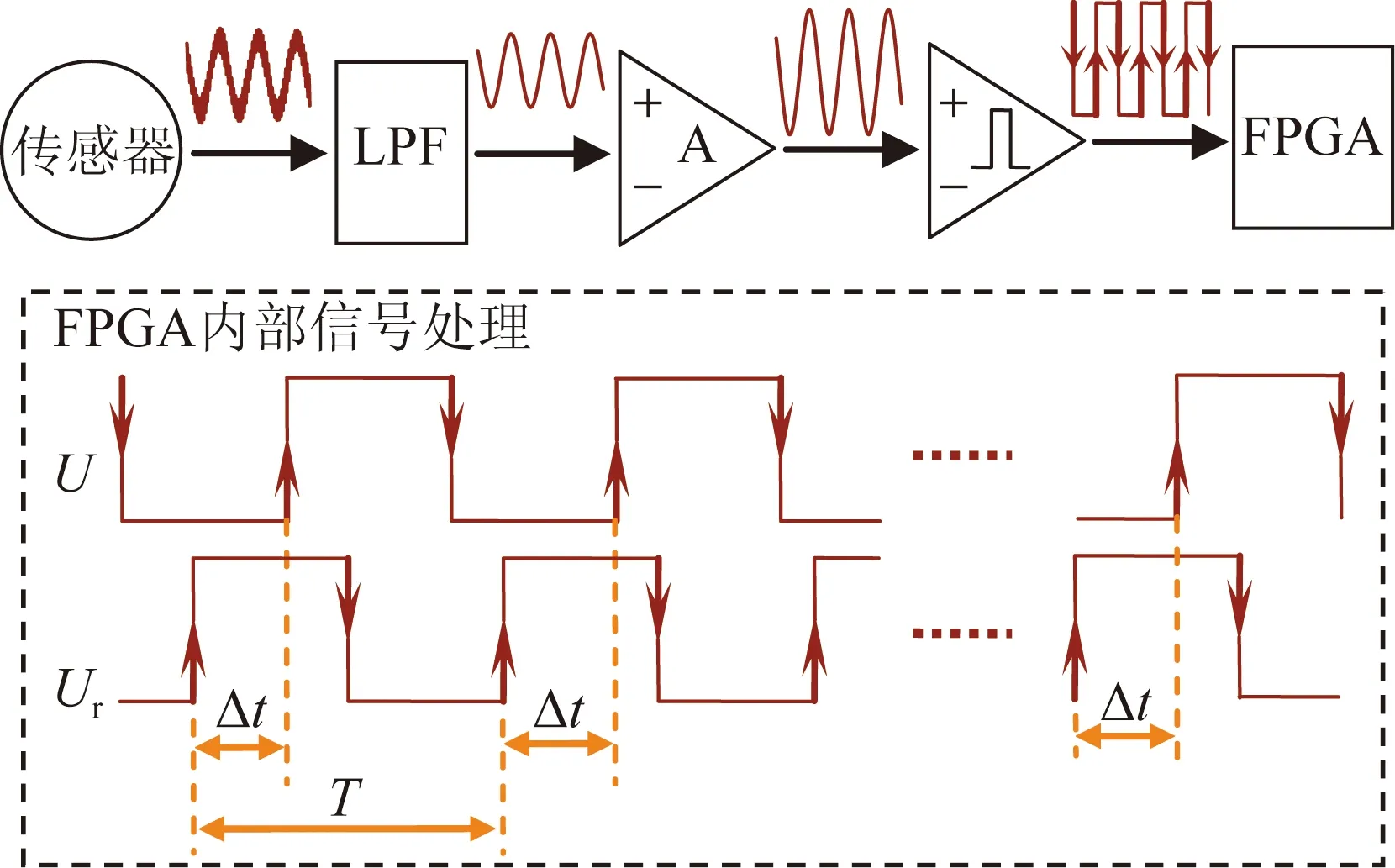
图3　传感器信号处理示意图

图3中，传感器输出的信号经低通滤波、放大和过零比较后转换为方波信号送入FPGA，与参考的同频信号Ur进行鉴相。该相位差由高频时钟脉冲进行插补，计算后得到传感器输出信号U与参考信号Ur的时间差Δt，根据时间差得到动测头相对定尺的位移x：

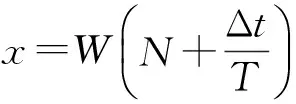
(11)

式中：N为动测头相对于定尺走过的完整极距数。

3　传感器不同测头姿态误差特性仿真

传感器在工作时，必须保证定尺和动测头的工作面(定尺工作面指定尺突出斜齿的上端面，动测头工作面指动测头导磁铁芯的下端面)与测量方向和被测运动平行，同时还应保证定尺和动测头工作面间的距离在重复安装时保持一致。

一般来说，定尺和动测头工作面需与被测运动平行，这是通过对定尺和动测头工作面与被测运动导向基准的平行度来保证的；定尺和动测头的测量方向与被测运动平行则是通过要求定尺和动测头侧向基准面(长侧面)与被测运动导向基准的平行度来保证的。

实际中，定尺和动测头的工作面与测量方向和被测运动是不可能严格平行的，定尺和动测头工作面间的距离在重复安装时也不可能保持完全一致。若以定尺x方向为测量方向和被测运动方向，则传感器动测头可能出现如下5种不同的姿态：动测头相对于定尺沿y轴或z轴偏移，动测头相对于定尺沿x轴、y轴或z轴旋转(分别称为滚转、俯仰和偏摆)，如图4所示。上述不同的测头姿态，均会使传感器输出的感应信号产生非线性变化，从而使位移测量产生附加误差。因此，在上述不同测头姿态下对模型的电磁场进行仿真，分析传感器在不同测头姿态下的误差特性，可有效指导传感器的设计和安装，以更好地发挥传感器的性能。

图4　传感器的不同测头姿态

3.1有限元建模及参数设置

ANSYS有限元分析软件有着强大的电磁场分析处理和求解功能，在实际工程中得到了广泛应用。本文利用ANSYS有限元分析软件Ansoft Maxwell进行仿真分析，并建立了如图4所示的传感器仿真模型。

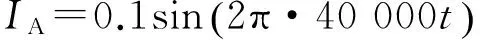
仿真中，动测头运动位移均设置为1个空间极距4 mm，运动步距为0.1 mm，因此仿真结果得到的是动测头在1个空间极距的40个不同空间位置的感应信号。

3.2偏移姿态下的误差特性仿真

一般来说，为了尽量消除边缘效应的影响，定尺宽度需大于动测头导磁铁芯的宽度，因此，动测头相对于定尺沿y方向的偏移对输出的影响极小。因此本文主要讨论动测头z向偏移下传感器输出信号的误差特性。

由仿真模型可知，动测头相对于定尺沿z向的偏移改变的实际是动测头和定尺工作面间的距离即气隙厚度d。图5为动测头和定尺在不同气隙厚度d下传感器感应线圈的输出仿真信号。

图5(彩图见期刊电子版)中，感应线圈输出的感应电势为一条条初相角不同的正弦信号，不同初相角对应着动测头运动到不同的空间位置。由于仿真中设置动测头运动1个空间极距，因此对应初相角刚好变化360°。

比较图5(a)～(d)可知，动测头和定尺间的气隙厚度d越大，感应信号越小。为获得不同气隙厚度下传感器输出信号的非线性误差，找出其误差特性，计算图5(a)～(d)中每条正弦曲线的初相角，并与理论初相角(相邻两条正弦曲线的理论初相角应相差360°/40=9°)相减，得到动测头在各空间位置的初相角误差，最后将其转换为对应的位移误差，如图6所示。

由图6可知，当动测头和定尺间具有不同气隙厚度时，位移误差的变化规律相似，均以4次误差为主。当动测头和定尺间的气隙厚度d=0.2 mm时，传感器输出信号的峰峰值约为19 V，此时位移总误差的峰峰值约为20.5 μm；当d=0.3 mm时，传感器输出信号的峰峰值约为12V，此时位移总误差的峰峰值约为15.9 μm；当d=0.4 mm时，传感器输出信号的峰峰值约为8 V，此时位移总误差的峰峰值约为16.2 μm；当d=0.5 mm时，传感器输出信号的峰峰值约为6V，此时位移总误差的峰峰值约为15.6 μm。由此可见，当动测头和定尺间的气隙厚度在0.3 mm时，既能获得较大的输出信号，又不致产生较大的位移误差。

(a)d=0.2 mm(b)d=0.3 mm

(c)d=0.4 mm(d)d=0.5 mm

Fig.5Simulation results when ruler and sensor-head have different gaps

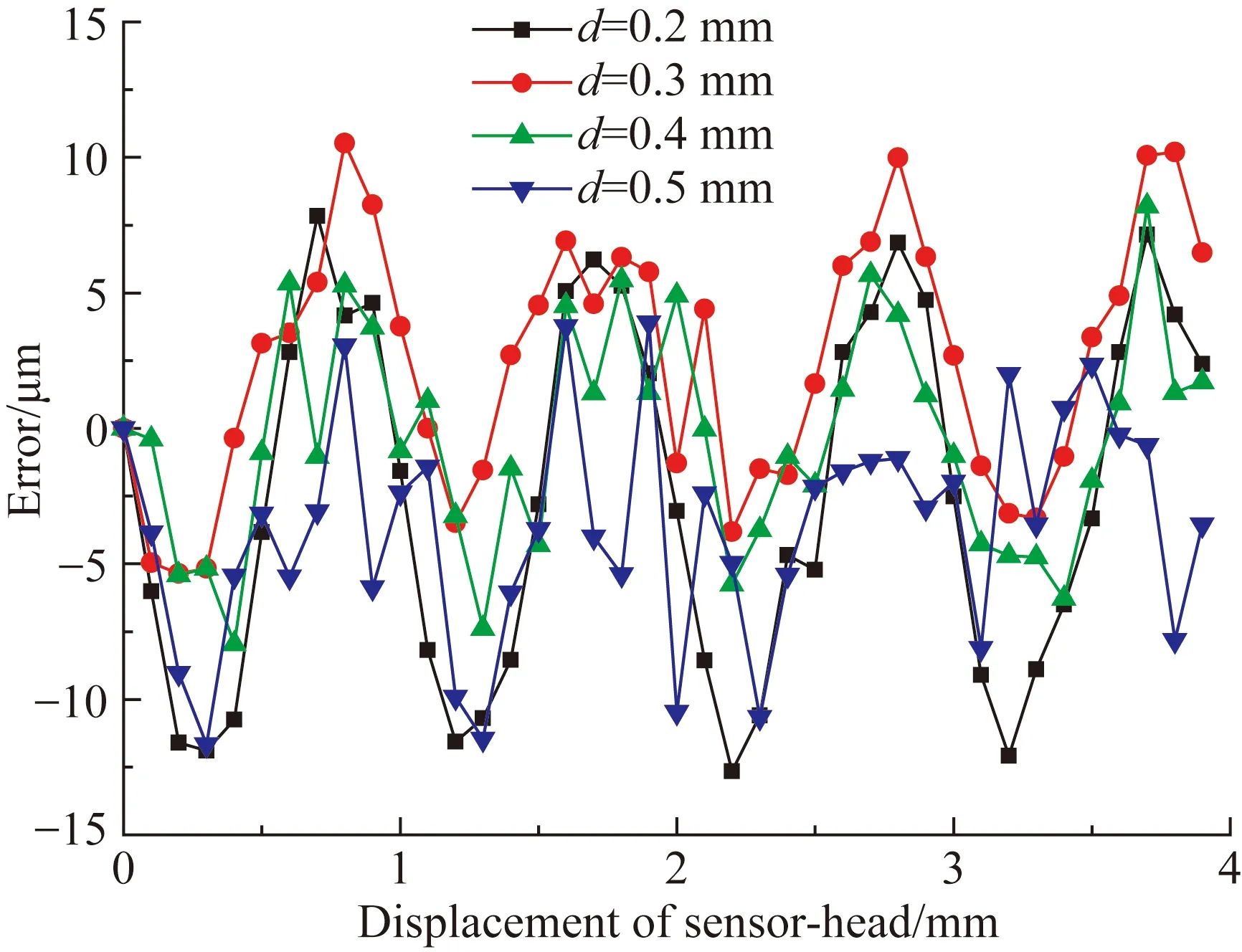
图6　不同气隙下动测头各位置的位移误差

Fig.6Displacement errors when the ruler and sensor-head have different gaps

3.3俯仰姿态下的误差特性仿真实验

俯仰姿态下，动测头工作面相对于定尺工作面有一个绕y轴旋转的倾角θy(见图7)，此时传感器输出信号的幅值将发生变化，使位移测量产生附加误差。实际安装中，对测头俯仰角度的调整通常是通过控制动测头沿x方向(工作长度)上倾角θy对应z轴方向的变化高度H1来实现的。

图7　测头俯仰示意图

图8(彩图见期刊电子版)为H1分别取0.02 mm 和0.04 mm，且动测头和定尺最小气隙厚度为0.3 mm时传感器感应线圈的输出仿真信号。

(a)H1=0.02 mm(b)H1=0.04 mm

同样计算图8(a)和(b)中每条正弦曲线的初相角和初相角误差，将其转换为对应的位移误差，如图9所示。

图9　不同俯仰姿态下动测头各位置的位移误差

Fig.9Displacement errors of model with sensor-heads under different pitch attitudes

由图9可知，动测头和定尺不平行会产生安装俯仰，从而使位移测量产生较大的附加误差。当H1=0.02 mm时，位移总误差的峰峰值约为54.3 μm，当H1=0.04 mm时，位移总误差的峰峰值约为88.6 μm。俯仰越大，位移测量产生的附加误差也越大。

3.4偏摆姿态下的误差特性仿真

偏摆姿态下，动测头工作面相对于定尺工作面有一个绕z轴旋转的倾角θz(见图10)，也会使传感器输出信号的幅值发生变化，产生附加位移测量误差。实际安装中，对测头偏摆的控制通常是通过控制动测头沿x方向(工作长度)上倾角θz对应y轴方向的变化高度H2来实现的。

图10　测头偏摆示意

由于定尺为开斜槽的矩形齿，因此，动测头相对于定尺的偏摆方向不同对输出信号的影响也不同。图11为不同偏摆下，动测头和定尺间最小气隙厚度为0.3 mm时模型的仿真结果。

(a)H2=0.02 mm(b)H2=0.04 mm

(c)H2=-0.02 mm(d)H2=-0.04 mm

仿真中，H2为正，表示动测头相对于定尺的偏摆方向与图10相同；H2为负，表示动测头相对于定尺的偏摆方向与图10相反。计算图11(a)～(d)中每条正弦曲线的初相角和初相角误差，并将其转换为对应的位移误差，如图12所示。

由图12(彩图见期刊电子版)可知，动测头和定尺不平行，会产生安装偏摆，但位移测量产生的附加误差极小。当H2=0.02 mm时，位移总误差的峰峰值约为20.0 μm；当H2=0.04 mm时，位移总误差的峰峰值仍约为20.0 μm；当H2=-0.02 mm 时，位移总误差的峰峰值约为18.2 μm；当H2=-0.04 mm 时，位移总误差的峰峰值约为16.8 μm。可以看出，偏摆对位移总误差的影响并不大，仅使位移误差发生极小变化，但这种微小的变化也可能是由于仿真时网格划分不对称、网格边长过大或者计算各行波初相角时引入的各种误差引起的。

图12　不同偏摆下动测头各位置的位移误差

3.5滚转姿态下的误差特性仿真

滚转姿态下，动测头工作面相对于定尺工作面有一个绕x轴旋转的倾角θx(见图13)，也会使位移测量产生附加误差。实际安装中，对测头滚转的控制通常是通过控制动测头沿y向(工作长度)上倾角θx对应z轴方向的变化高度H3来实现的。

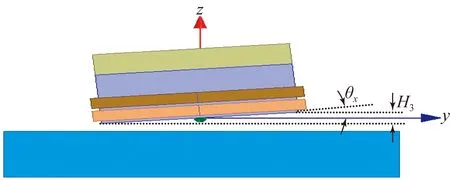
图13　安装滚转示意图

图14为动测头中心和定尺最小气隙厚度为0.3 mm时，不同滚转姿态下模型的仿真结果。

(a)H3=0.01 mm(b)H3=0.02 mm

Fig.14Simulation results of model when sensor-head under different rotation angles aroundx-axis

计算图14(a)和14(b)中各条正弦曲线的初相角和初相角误差，并将其转换为对应的位移误差，如图15所示。

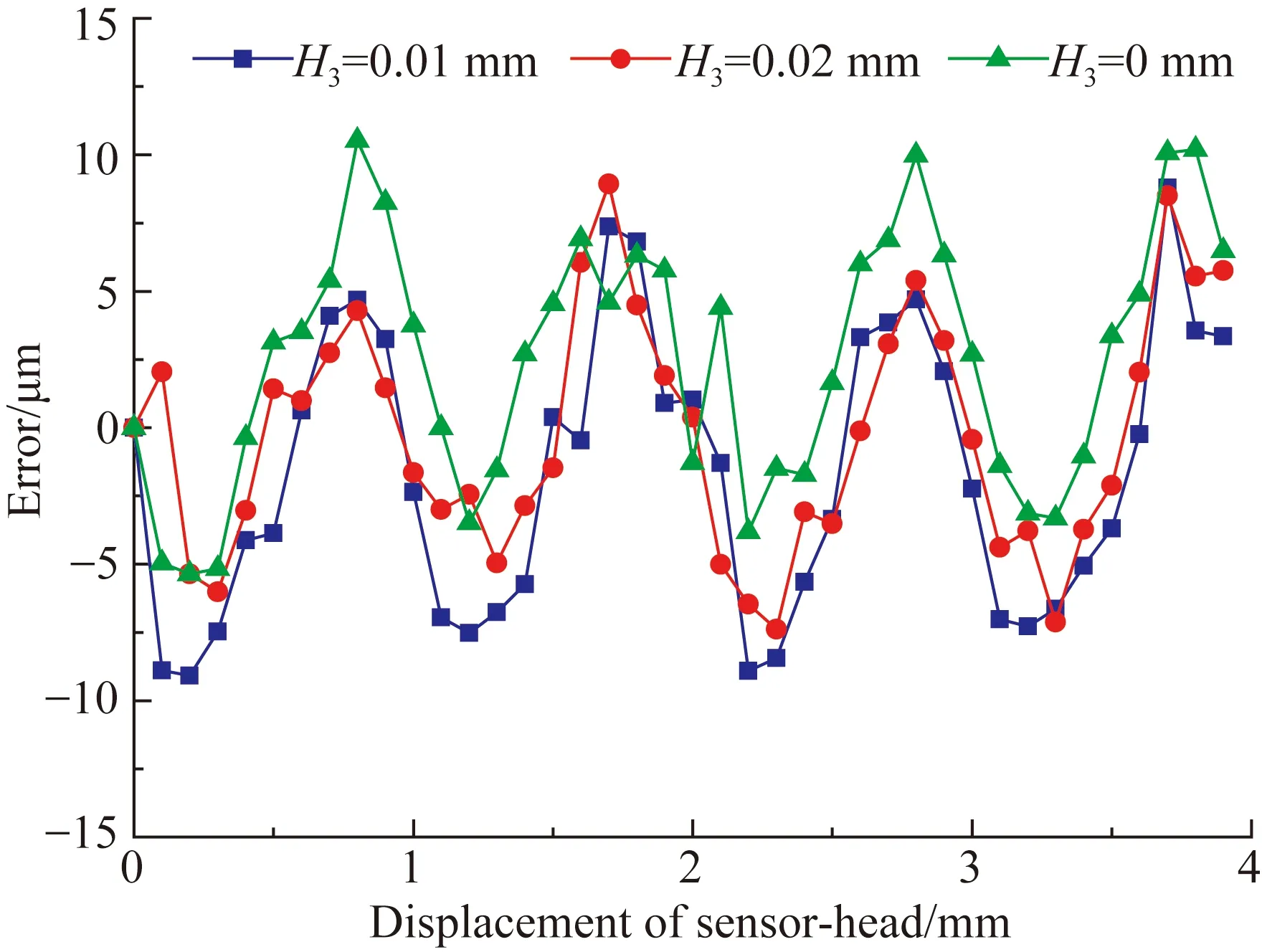
图15　不同滚转姿态下动测头各位置的位移误差

Fig.15Displacement error of model when sensor-head under different rotation angles aroundx-axis

由图15可知，动测头和定尺不平行，会产生安装滚转，位移测量产生的附加误差也极小。当H3=0.01 mm时，位移总误差的峰峰值约为17.9 μm；当H2=0.02 mm时，位移总误差的峰峰值仍为16.3 μm。随着滚转角变大，位移总误差反而略有减小，当然，这种微小变化也可能是由仿真时网格划分不对称、网格边长过大或者计算各行波初相角时引入的误差引起的。

3.6不同测头姿态下的误差特性比较

为综合比较且进一步研究不同测头姿态下的误差特性，对图6、图9、图12、图15中各条位移误差曲线进行FFT分析，得到不同测头姿态下位移误差各次谐波的幅值和相角。其中，各曲线幅值较大的前10次谐波的幅值和相角如表1所示。

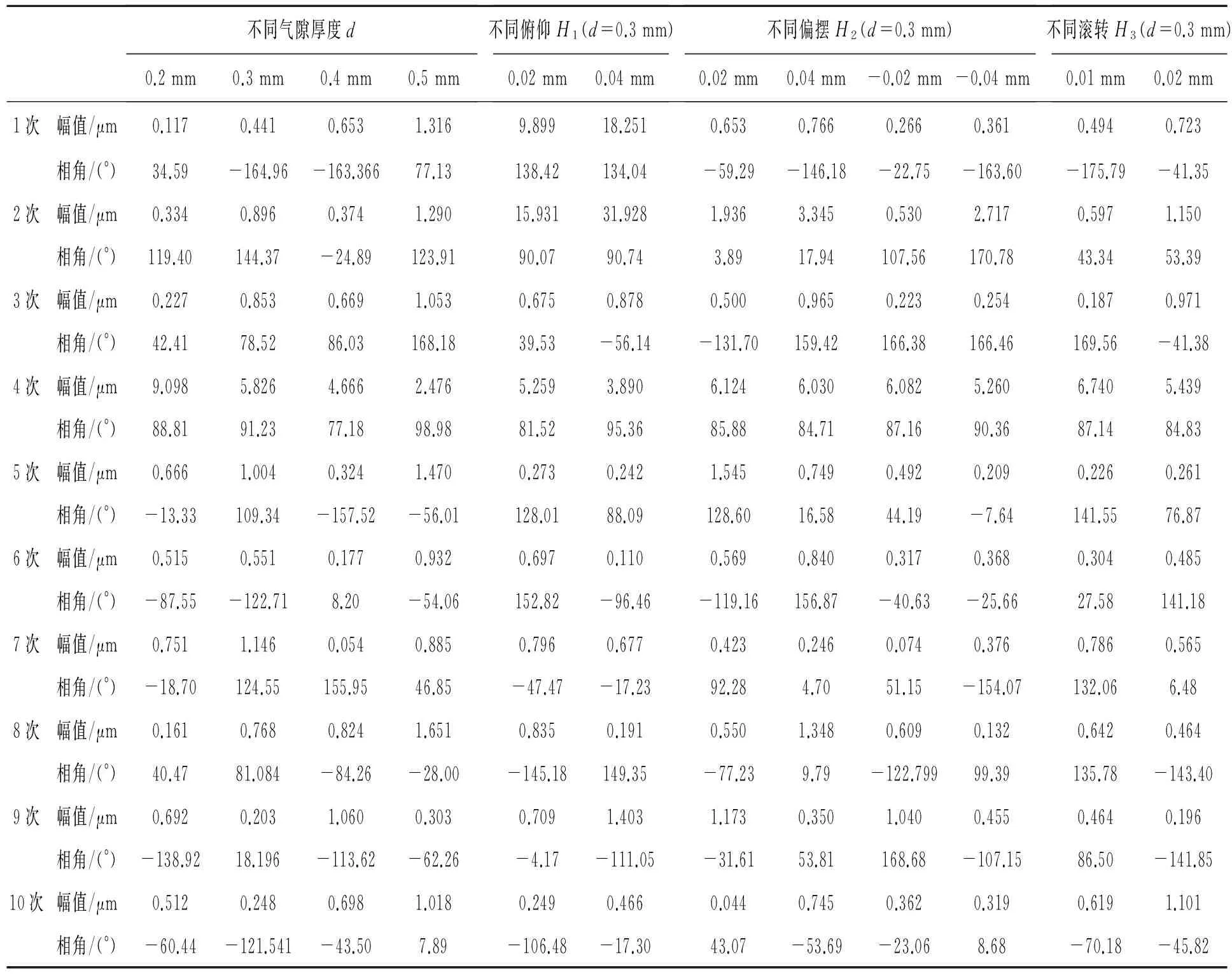
表1　不同测头姿态下误差主要频次的幅值和相角仿真结果比较

由表1可知，测头俯仰姿态下，会使位移测量产生较大的1次和2次附加误差。当H1=0.02 mm 时，由测头俯仰产生的位移测量1次附加误差约为9.5 μm，2次附加误差约为15 μm；当H1=0.04 mm时，由测头俯仰产生的位移测量1次附加误差约为17.8 μm，2次附加误差约为31 μm。俯仰角越大，1次和2次附加误差也越大。测头偏摆和测头滚转引入的各次附加误差均较小，在控制测头偏摆高度H2不超过0.04 mm 和测头滚转高度H3不超过0.02 mm时，由偏摆和滚转引起的各次位移测量附加误差均不会超过3 μm。因此，安装传感器时，应尽量控制测头不发生俯仰，以避免产生较大的位移测量附加误差。

4　实验验证与分析

根据仿真分析的结果，加工了图16的定尺和动测头(尺寸参数与前述仿真模型一致)。其中，定尺和动测头的导磁铁芯采用慢走丝线切割工艺加工而成，同时，对定尺底面和侧面，以及导磁铁芯的工作面进行磨削加工，以保证其平面度均小于0.002/200 mm。加工完成后，通过联结板将两独立测头的导磁铁芯固定并安装于动测头壳体内。激励线圈和感应线圈采用特制的双线并绕矩形线圈(各100匝，直流阻抗约为9 Ω)，套于导磁铁芯的矩形齿上，并根据模型中的绕向要求进行串接。

(a)动测头

(b)定尺

4.1实验验证

搭建了图17所示的实验平台，进行位移测量。图17中，时栅传感器的定尺固定在花岗石平台上，动测头则安装于AEROTECH精密直线气浮平台ABL2000上，通过驱动装置控制动测头相对定尺的直线运动。通过信号处理电路对动测头的输出信号进行位移解算，并送入计算机显示。

图17　实验平台

采用RENISHAW XL-80激光干涉仪作为参考标准器，检验不同测头姿态下的位移测量误差。为减小随机误差的影响，以下数据均为5次测量的平均值。

实验中，首先安装好定尺，为获得动测头和定尺不同气隙厚度下的误差特性，安装动测头时，保证在其工作长度上俯仰不超过0.004 mm，偏摆不超过0.004 mm，滚转不超过0.002 mm。然后调整定尺和动测头间的气隙厚度，使动测头工作面中心到定尺工作面的距离分别为0.2、0.3、0.4和0.5 mm。图18为时栅传感器在不同气隙厚度下动测头运动1个空间极距的测量数据与RENISHAW ML80激光干涉仪测得数据比对后的结果。

重新安装动测头，保证在测头工作长度上的偏摆不超过0.004 mm，滚转不超过0.002 mm，但俯仰高度H1约等于0.02 mm和0.04 mm。图19为动测头运动1个空间极距的测量数据与RENISHAW ML80激光干涉仪测得数据比对后的结果。由图19可知，测头俯仰姿态下，引入了较大的位移测量附加误差。

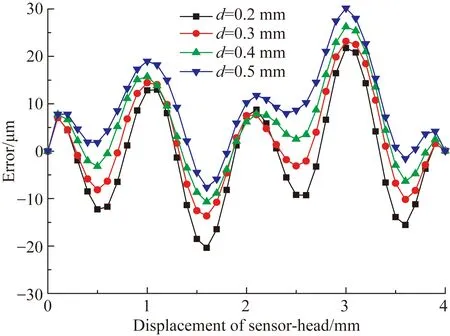
图18　不同气隙厚度下位移误差实验数据

Fig.18Experiment data of displacement error when ruler and sensor-head have different gaps

图19　不同俯仰姿态下的测量误差

Fig.19Displacement error of physical sensor-head under different pitch attitudes

再次安装动测头，保证在测头工作长度上的俯仰不超过0.004 mm，滚转不超过0.002 mm，但偏摆高度H1分别约等于0.02、0.04、-0.02 和-0.04 mm。图20为动测头运动1个空间极距的测量数据与RENISHAW ML80激光干涉仪测得数据比对后的结果。

最后调整动测头，保证在测头工作长度上的俯仰不超过0.004 mm，偏摆不超过0.004 mm，但滚转高度约等于0.01 mm和0.02 mm。图21为动测头运动1个空间极距的测量数据与RENISHAW ML80激光干涉仪测得数据比对后的结果。

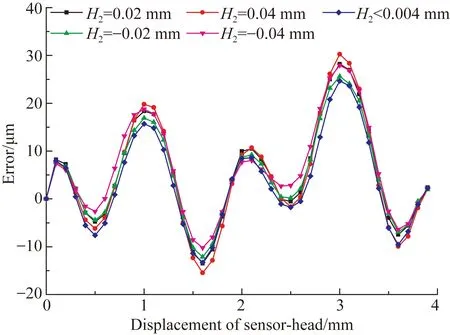
图20　不同偏摆姿态下的测量误差

Fig.20Displacement error of physical sensor-head under different yaw attitudes

图21　不同滚转俯仰姿态下的测量误差

Fig.21Displacement error of physical sensor-head under different rotation angles aroundx-axis

表2为各种不同测头姿态下误差主要频次的幅值和相角。

4.2实验结果分析

比较表1和表2的结果，可知：

(1)与仿真结果相比，表2中实际测量误差的1次、2次和4次幅值明显增大，这是由于仿真中动测头两独立测头(测头一和测头二)的一致性较好(无加工误差，两独立测头完全一样)，而实际加工出来两独立测头的一致性相对较差(存在加工误差，两独立测头并不完全一样)所致，从而也说明测头的一致性对1次、2次和4次谐波的影响较大，对其余各次谐波的影响较小。

表2　不同测头姿态下误差主要频次的幅值和相角实验结果比较

(2)气隙厚度越大，位移误差1次和2次谐波的幅值越大，4次谐波的幅值越小；俯仰高度变大，位移误差1次和2次谐波的幅值增大的非常快，但4次谐波的幅值略有减小；相比较而言，不同偏摆和不同滚转对测量误差的影响较小，偏摆对2次误差幅值的影响相对较大，而滚转对各次谐波幅值的影响均更小。

(3)位移误差除1次、2次和4次谐波外，其余各次谐波的幅值均较小，这与仿真结果相似，而且测量数据均为5次测量的平均值，消除了部分随机误差的影响。

(4)仿真中虽然测头的一致性较好，但和实际测量结果相比，除1次、2次和4次谐波幅值相差较大外，其余各次谐波的幅值与实际测量结果差不多，这是由于仿真结果中还包含了一些其他误差，如仿真时网格划分不对称、网格边长过大引起的误差等等。

5　结　论

通过对时栅传感器原理的进一步分析，本文提出了一种新型的变耦型时栅直线位移传感器。传感器采用同时绕有激励和感应线圈的两个独立测头组成的动测头相对定尺做空间运动，实现了将两路驻波信号合成为行波信号，进行位移测量，系统成本低廉、极易制造。

对传感器不同测头姿态下的误差特性进行了仿真研究，并进行了实验验证。仿真和实验结果均表明，各种测头姿态下，对位移误差的1次、2次和4次谐波均影响较大，对其余各次谐波的影响较小。其中，俯仰姿态下，传感器引入的附加误差最大，而不同气隙厚度、不同偏摆和不同滚转姿态下，传感器引入的附加误差相对较小。仿真结果与实验结果基本一致，因此，为保证传感器的精度，应着重控制传感器测头的俯仰。

最终实验结果表明，在较好的安装条件下，即气隙厚度约为0.3 mm，并控制俯仰不超过0.004 mm，偏摆不超过0.004 mm，滚转不超过0.002 mm 的情况下，传感器的原始精度可以达到±18 μm，且经过标定补偿后还能实现更高的精度。

上述系统的仿真和实验研究，验证了控制传感器的测头姿态可以提高传感器的测量精度。本文的研究结果可用于指导传感器的安装和误差分析。

[1]彭东林，刘小康，张兴红.高精度时栅位移传感器研究[J].机械工程学报，2005，41(12)：126-129.

PENG D L，LIU X K，ZHANG X H. Research on high-precision time-grating displacement sensor [J].ChineseJournalofMechanicalEngineering，2005，41(12)：126-129.(in Chinese)

[2]TANG Q F，PENG D L，WU L，etal..An inductive angular displacement sensor based on planar coil and contrate rotor [J].IEEESensorsJournal，2015，15(7)：3947-3954.

[3]彭东林，李彦，付敏，等.用于极端和特殊条件下机械传动误差检测的寄生式时栅研究[J].仪器仪表学报，2013，34(2)：359-365.

PENG D L，LI Y，FU M，etal..Study on parasitic time grating sensors used for mechanical transmission error measurement under harsh and special environment [J].ChineseJournalofScientificInstrument，2013，34(2)：359-365.(in Chinese)

[4]孙世政，彭东林，武亮，等.时栅动态测量误差建模与补偿技术研究[J].机械工程学报，2014，50(22)：10-15.

SUN SH ZH，PENG D L，WU L，etal..Research on modeling and compensation technology for time-grating sensor’s dynamic measurement errors [J].ChineseJournalofMechanicalEngineering，2014，50(22)：10-15.(in Chinese)

[5]高忠华，彭东林.直线时栅测量系统的误差研究[J].电子测量与仪器学报，2013，27(1)：15-20.

GAO ZH H，PENG D L.Study on error of linear time grating measurement system [J].JournalofElectronicMeasurementandInstrument，2013，27(1)：15-20.(in Chinese)

[6]杨继森，李小雨，张静，等.时栅位移传感器动态误差模型及修正算法研究[J].仪器仪表学报，2015，36(11)：2548-2555.YANG J S，LI X Y，ZHANG J，etal..Study on the dynamic error model and correction algorithm of time grating displacement sensor [J].ChineseJournalofScientificInstrument，2015，36(11)：2548-2555.(in Chinese)

[7]鲁进，陈锡侯，彭东林，等.基于双测头的时栅位移传感器自标定方法[J].仪表技术与传感器，2013，34(2)：78-81.LU J，CHEN X H，PENG D L，etal..Research of self-calibration method for time grating displacement sensor based on two read heads [J].InstrumentTechniqueandSensor，2013，34(2)：78-81.(in Chinese)

[8]刘小康，彭凯，王先全，等.纳米时栅位移传感器的理论模型与误差分析[J].仪器仪表学报，2014，35(5)：1136-1142.LIU X K，PENG K，WANG X Q，etal..Theoretical model and error analysis of nanometer time grating displacement sensor [J].ChineseJournalofScientificInstrument，2014，35(5)：1136-1142.(in Chinese)

[9]汤其富，彭东林，武亮，等.时栅角位移传感器中的多普勒效应影响及其抑制方法研究[J].仪器仪表学报，2014，35(3)：620-626.

TANG Q F，PENG D L，WU L，etal..Study on the influence of Doppler effect and its suppressing method in time grating angular displacement sensor [J].ChineseJournalofScientificInstrument，2014，35(3)：620-626.(in Chinese)

[10]刘小康，蒲红吉，郑方燕，等.纳米时栅位移传感器电场分布与误差特性研究[J].仪器仪表学报，2013，34(10)：2257-2264.

LIU X K，PU H J，ZHENG F Y，etal..Research on electric field distribution and error characteristics of the nanometer time grating displacement sensor [J].ChineseJournalofScientificInstrument，2013，34(10)：2257-2264.(in Chinese)

[11]孙世政，陈锡侯，彭东林，等.嵌入式时栅传感器的动态自标定[J].光学 精密工程，2014，22(10)：2757-2764.

SUN SH ZH，CHEN X H，PENG D L，etal..Dynamic self-calibration for embedded time grating sensors [J].Opt.PrecisionEng.，2014，22(10)：2757-2764.(in Chinese)

[12]陈锡侯，苟李，官云丽，等.基于单个读数头的角位移传感器自标定方法[J].传感技术学报，2014，27(8)：1049-1053.

CHEN X H，GOU L，GUAN Y L，etal..A self-calibration method of angular displacement sensor based on single reading head [J].ChineseJournalofSensorsAndActuators，2014，27(8)：1049-1053.(in Chinese)

鲁进(1980-)，女，重庆人，讲师，2003年、2006年于重庆大学分别获得学士、硕士学位，主要从事精密测量与智能传感器方面的研究。E-mail: jinlu@cqut.edu.cn

陈锡侯(1976-)，男，福建漳州人，教授，硕士生导师，1999年、2004年、2007年于重庆大学分别获得学士、硕士、博士学位，主要从事精密测量与智能传感器方面的研究。E-mail: cxh0458@cqut.edu.cn

(本栏目编辑：马健)

(版权所有未经许可不得转载)

Variable coupling time grating sensor and effects of sensor-head attitudes on measuring errors

LU Jin1*， CHEN Xi-hou2， TANG Qi-fu2， WU Liang2

(1.SchoolofElectronicInformationandAutomation，ChongqingUniversityofTechnology，Chongqing400054，China；2.ChongqingKeyLaboratoryofTime-GratingSensingandAdvancedTestingTechnology，ChongqingUniversityofTechnology，Chongqing400054，China)*Correspondingauthor，E-mail：jinlu@cqut.edu.cn

On the basis of the measuring principle of time grating sensors， a new variable coupling time grating displacement sensor was proposed by employing a high-frequency pulse as measurement basis to improve the precision of displacement measurement. The precision displacement measurement of the sensor was implemented by changing the coupling state of excitation and induction coils to output a traveling wave signal for inducing the displacement change. By modeling and simulations， the displacement error characteristics of the sensor when sensor-head was in different attitudes were obtained. The harmonics analysis was performed， and the influence of different sensor-head attitudes on different resonances of the displacement measurement errors was obtained. A sensor prototype was designed based on the model and then experiments were carried out. Simulations and actual experiments indicate that different sensor-head attitudes mainly influence 1st， 2nd and 4th harmonics， and other harmonics are more sensitive to pitch attitudes than other attitudes of the sensor-head. When the sensor-head is in a good attitude and the gap between ruler and sensor-head is 0.3 mm， both experimental analysis and simulation result show that the measurement error is about ±18 μm. Simulations and actual verification experiments are in agreement well.

time grating sensor; displacement measurement; sensor-head attitude; mounting error; measuring precision

2016-03-04；

2016-06-21.

国家自然科学基金资助项目(No.51505052，No.51405049)；重庆市科技研发基地能力提升项目(No.cstc2014pt-sy40002)

1004-924X(2016)09-2271-12

TP212.12

A

10.3788/OPE.20162409.2271