大规模优化设计在HAJIF系统中的实现

王立凯，郭瑜超，罗利龙

(中国飞机强度研究所，陕西 西安 710065)



大规模优化设计在HAJIF系统中的实现

王立凯，郭瑜超，罗利龙

(中国飞机强度研究所，陕西 西安 710065)

针对分析模型精细化带来的大规模变量结构优化设计问题，深入系统地研究了大规模结构优化设计求解理论，并在HAJIF(航空结构强度分析与优化设计软件系统)中予以实现。HAJIF是一个十分有用的分析及优化软件，然而随着工程问题的日益庞大，该系统表现出设计规模受限的技术瓶颈，从而限制了它的广泛应用。本文通过一系列的理论改进突破了HAJIF系统中的一些关键问题，使得当前系统可处理设计变量达到10万量级。这些方法包括约束删除、约束区域化、变量处理、敏度分析等。

大规模结构优化；解析法；约束分区处理；数学规划法

1 引 言

经过几十年的持续发展，大型飞机设计逐渐从粗放型设计向精细化设计转换，早期限于分析工具的性能而被简化掉的很多结构细节特征被引入到结构分析模型中来，使得分析模型规模不断增大，导致优化模型规模呈爆炸式增长。当前，国际上对优化设计变量数目的需求已经达到10万量级。大规模结构优化需要同时考虑规模和效率问题。基于敏度信息的数学规划法具有收敛快、精度高等优点，在航空结构优化中得到广泛应用。

虽然数学规划法本身的理论非常清晰，但将该理论用于工程软件中便涉及到有限元技术、计算机软件技术及结构强度理论等多个学科领域的问题。由于HAJIF系统具备完备的求解器、优化器及算法库，因此，大规模、多变量的工程问题在当前HAJIF的理论体系及软件框架上进行修改完善是比较现实有效的。课题组通过对多个方面的理论研究，提高了HAJIF系统对大规模、多变量问题的解决能力。最后以HAJIF2013系统为基础平台开发了大规模变量结构优化模块，并采用机翼细节模型进行了算例验证。

2 HAJIF简介

HAJIF[1]是中国飞机强度研究所自主研制推出的国内航空界功能最为全面的大型CAE软件系统。该系统以强度试验数据库为支撑，提供了飞行器结构静强度、动强度、热强度、气动弹性、结构优化设计等基本求解功能，以及飞机结构细节强度校核、耐久性等特色分析功能。在我国航空业发展的早期，HAJIF系列软件发挥了重要作用，尤其是其优化设计功能，在我国多个现役型号设计中得到应用。当前，随着计算机硬件技术的发展，飞机结构设计中越来越多地采用细节模型，分析模型往往达到百万节点、设计变量达到数万量级。在对这类采用精细有限元方法建立的模型进行优化时，HAJIF系统显示出优化规模偏小的技术瓶颈。

3 大规模优化策略研究

虽然数学规划法本身的理论非常清晰，但将该理论用于工程软件中，便涉及多个学科的问题，如有限元技术、计算机软件技术及数值计算等。本研究通过对以下几个方面的理论研究来提高HAJIF系统对大规模、多变量问题的解决能力。

3.1 敏度计算[2]

结合灵敏度分析来确定优化过程中设计点的移动方向，通过结构响应对于各设计变量的导数，用以确定最有效的结构修改部位与量值，确保大型复杂结构的优化设计取得成功。灵敏度分析的方法有解析法、半解析法和数值法。灵敏度分析计算过程是整个优化过程中最耗时的一个步骤，约占总用时的70%[3]。大规模设计问题一般都有约束多的特点，而其中绝大部分约束是诸如位移、应力、应变等静强度约束。本文对静强度约束的敏度计算作如下推导：

静强度约束导数的计算：

(1)

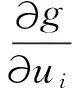
(2)

直接法：

(3)

伴随法(引入伴随向量λ)：

kλ=z

(4)

λ类似于在载荷向量z作用下的位移。伴随法也称为虚载荷法，因为常把z描述成一个虚载荷。直接法和虚载荷法的计算量主要取决于约束数和设计变量数。对于每一个设计变量，直接法需求解方程(1)一次，而虚载荷法求解方程(4)一次。因此，当设计变量数远小于约束数时，直接法比虚载荷法[4]有效；设计变量数远多于约束数时，虚载荷法更有效。当前，HAJIF系统采用的是直接法，通过对系统中的静强度约束导数[5-6]计算部分加入虚载荷法，由程序根据设计变量数与约束数的关系来选择相应的敏度计算流程，可极大地提高计算效率。

3.2 变量处理

大规模问题的特点是变量多、约束多，解决大规模问题首要的是提高对大规模设计变量的解决，采用新的变量处理技术来提高HAJIF系统对大规模设计变量的处理能力，本文采用以下两种技术：

(1)变量耦合

HAJIF系统当前主要采用不同设计区不同设计变量的方法，即设计变量之间是独立的，没有任何的耦合关系。而对于复杂的结构问题，必须采用大量的设计变量。在程序中通过引入变量连接技术，即利用少数的一些设计变量来控制一个复杂的结构，从而使设计过程中的变量数大量减少。图1所示为一个悬臂板模型，理想的结构方式中，每一个单元的厚度都是不同的。要做到这一点，如果按照常规的方法建立优化模型，就必须采用按单元设计的方案，即每一个有限单元为一个设计变量。而引入了变量连接技术后，可以用极少的几个变量来定义设计模型。

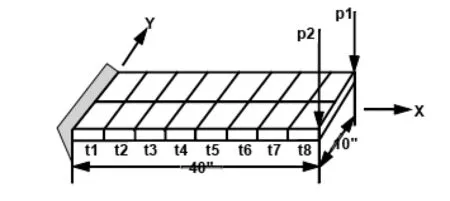
图1 悬臂板模型

为减少设计变量的个数，程序中引入了多项式变量耦合与自定义变量耦合两种变量耦合方式。多项式变量耦合由输入的优化数据文件来确定设计变量的耦合形式，采用多项式变量耦合得到元素的特征尺寸。

自定义变量耦合由用户根据工程实际定义变量到元素的耦合形式，例如，第l块中变量耦合形式详见下式：

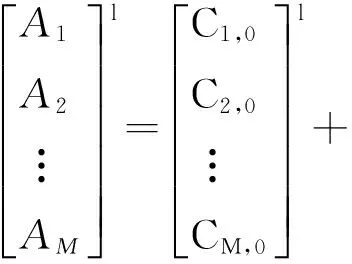
(5)

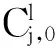
(2)区分变量为主动变量和被动变量

根据灵敏度分析，预先估计变量的变化所导致的目标函数的变化，从而在迭代过程中只对灵敏度高的设计变量进行分析，这将极大地提高求解效率，即临时删除不敏感的变量。具体实现过程可采用如下步骤：首次迭代时，对所有的设计变量进行灵敏度分析，而在后续的几次设计中，只对灵敏度高的设计变量进行调整，循环几次后再对所有变量进行一次灵敏度分析，对各变量的灵敏度大小重新排序，如此反复，直到迭代完成。在迭代过程中，主被动元会起变化，常有交换，因此每次迭代都必须首先判断和划分主被动元。

3.3 约束处理

大规模设计问题必须对约束进行必要的处理。对大规模的结构优化设计可利用无效约束删除技术，在优化过程中临时删除那些具有足够可行性，又不太可能在设计变量做适度修改时变为临界约束的那些约束条件，以减少约束数，降低求解的规模[3]。一般地，约束有等式约束和不等式约束两种，等式约束可采用下述形式转化成两个不等式约束。例如gk(x)=0为一等式约束，则要求：

(6)

这两个绝对值相等、符号相异的不等式约束将迫使gk(x)=0。但需注意的是，有些优化算法将因此而失败，原因是梯度矩阵会出现奇异。所以，在优化系统中，一般只处理不等式约束。为使数值稳定起见，结构性状约束均应进行范化，即无因次处理，取-1.0与0.0之间的值，以使各约束对设计变量的改变有足够的敏度。例如，如果应力约束是-0.1，位移约束也是-0.1，那就意味着每种约束都在其容许值的10%之内；如果不采用范化的话，应力限是20,000，即只有当应力值是19,999.9时，该约束才是有效的。约束范化采用统一的形式：

对于结构性状的下限：

(7)

对于结构性状的上限：

(8)

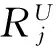
通过对约束正则化公式(7)、(8)的分析可以看出，若某一约束gj(x)值为1.0，即意味着约束被大大地超出，而如果某一约束gj(x)的值为-0.5，即意味着它至临界限还有一定的距离。根据有约束优化的极值条件(Kuhn-Tucker条件)可知道，最佳设计必定位于约束边界处，即约束临界值处，因而对于此类小于临界值的约束条件，可以引入一个约束阀值(threshold)，在程序中默认值为-0.5，每类性状约束可选择不同大小的阀值，以重点突出重要的约束。当某一约束gj(x)小于该阀值时，认为其对当前设计不起作用——无效约束，即约束必定得到满足，从而在当前设计过程中可以将其临时删除掉，而仅仅保留那些大于阀值的约束——有效约束，其过程如图2所示。

图2 约束删除示意图

通过约束删除技术，可以一定程度地缩小约束的规模。对于大量存在的应力约束，还可利用约束区域化的方法将约束数进一步减少。例如机翼蒙皮部分，在分析中以一系列的壳单元模拟，从制造方面考虑其由几个大块组成，同一块中的厚度是一样的。在分析时，如果某一部分有几个单元应力过高，若将该部分加厚使得应力最大的那一个单元得以满足的话，则同一区域的其它元素也必定得到满足。因此，在优化设计中，在同一区中只保留约束最大的几个约束，在HAJIF系统中默认每一区只保留两个应力约束，通过约束删除和区域化处理，可以将计算规模降低一到二个数量级，其过程如图3所示。

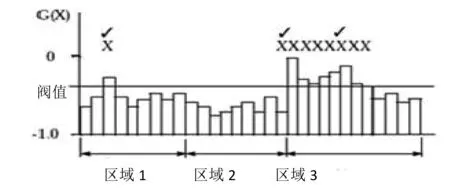
图3 约束删除示意图

严格来讲，当gj(x)≥0即认为约束被违背，但在实际中，由于载荷、材料性能以及有限元方法本身对响应计算的近似性等原因，约束不可能正好为0，因此，在程序中取一个很小的数来代替零值(默认为0.003)，允许响应值有0.3%的误差量，即只有当gj(x)>0.003时，认为约束被违背。归结起来，即在程序中以下面几个公式来判定约束状态：

(9)

4 程序组织

HAJIF系统中，各模块的调用关系[7-9]较为复杂，总的关系如图4所示。对HAJIF系统，要通过扩大其对敏度计算效率、多变量及多约束的处理能力等多个方面来综合提高系统对大规模问题的求解能力，对HAJIF系统的改造不仅涉及各个功能模块本身，而且涉及到对数据文件进行统一的管理。

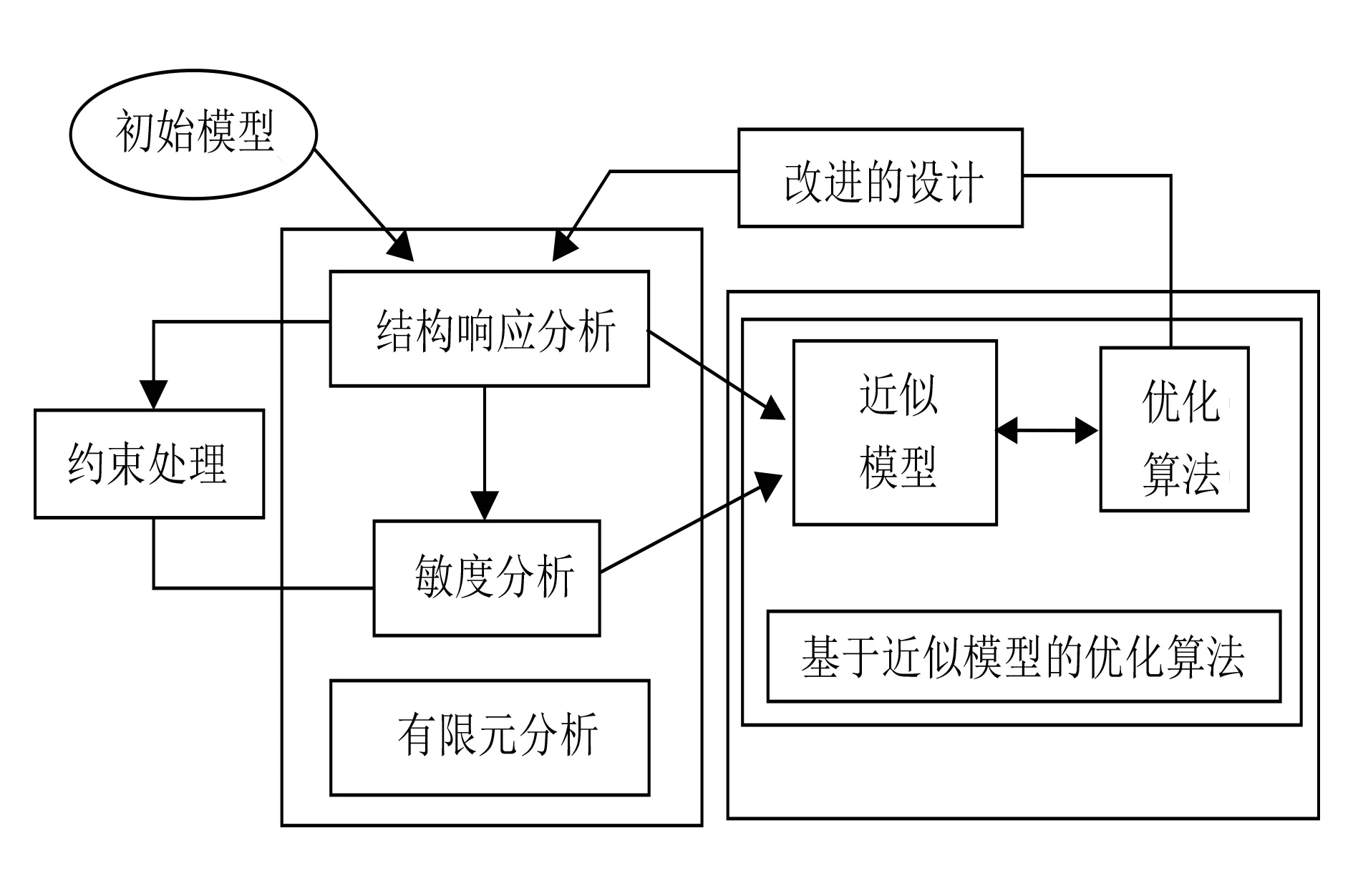
图4 HAJIF系统优化模块的流程图

5 算 例

图5所示为全复合材料常规布局翼盒的精细化模型，沿展向布置27根肋，前后布置两根大梁，共包含40862个单元，29542个节点。优化模型以复合材料壳单元分层厚度和梁单元的截面面积为设计变量，除根肋外，从翼根到翼稍每个梁肋交点处布置一个沿升力方向的位移约束来控制机翼各剖面的弯曲刚度，同一根肋的前后交点布置一个扭角约束来控制机翼各剖面的扭转刚度，全模型共计设计变量115360个，位移和扭角约束共计78个，全结构初始重量为2237.62kg。

图5 精细化机翼盒段

采用本文方法，在具备300个计算节点的计算机集群上对上述优化问题进行求解，经过9步迭代后优化收敛，共用时约143min，优化后结构重量为2038.47kg，在满足约束的前提下实现减重199.15kg，占结构初始重量的8.9%。重量迭代过程如图6所示。

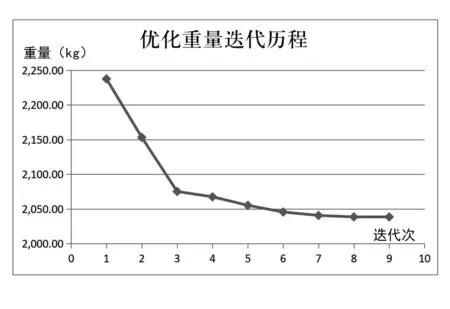
图6 优化重量迭代历程

6 结 论

通过利用大规模优化设计计算获得的结果与以往变量数受限时采用的分级包络设计结果进行比较发现，在扩大规模后的迭代趋势与分级包络设计趋势完全一致且目标函数值略有降低，证明现有HAJIF系统在处理多变量的结构优化问题上是有效的。通过比较可以发现，由于设计规模所限，在以往的计算中采用分步的设计方法，而在程序改造后则可一次完成设计，可见程序改造后保证了计算结果的正确性，提高了设计效率，并得到了更优的设计点。

[1]丁惠梁,孙侠生,黄琦.COMPASS子结构分析与敏度计算方案[Z].COMPASS系统工程办公室,1988.

[2]Gregory J.Moore. Design Sensitivity and Optimization User’s Guide[Z]. MSC.Nastran Version 68.

[3]Uwe Reuter, Zeeshan Mehmood. Efficient classification based methods for global sensitivity analysis[J]. Computers and Structures 110-111 (2012) 79-92,2012.

[4]Su Huan Chen, Ping Liang, Wan Zhi Han. A new method of sensitivity analysis of static responses for finite element systems[J]. Finite Elements in Analysis and Design, 29(1998) 187-203,1998.

[5]Olhoff, Niels, Rasmussen, John and Lund. A Method of “Exact” Numerical Differentiation for Error Elimination in Finite-Element-Based Semi-Analytical Shape Sensitivity Analyses[J]. Mechanics Based Design of Structures and Machines, 2009,21(1):1-66.

[6]Morsaleen Shehzad Chowdhury, Chongmin Song, Wei Gao. Shape sensitivity analysis of stress intensity factors by the scaled boundary finite element method[J]. Engineering Fracture Mechanics, 116 (2014) 13-30,2014.

[7]孙侠生,丁惠梁,黄琦.COMPASS优化设计块技术任务书[Z]. COMPASS系统工程办公室,1988.

[8]段世慧.COMPASS实用元素库设计[Z]. COMPASS系统工程办公室,1988.

[9]卢叔全.COMPASS颤振分析部分计算方案[Z].COMPASS系统工程办公室,1989.

Realization of Large-scale Optimization Design in HAJIF System

Wang Likai, Guo Yuchao, Luo Lilong

(Aircraft Strength Research Institute of China, Xi′an 710065, Shaanxi, China)

The scale of the optimization problem becomes larger and larger because of the refined FE model. This paper focused on solving this difficulty by a serious of efforts. HAJIF is a very useful tool for structural analysis and optimization for aircraft structures. HAJIF new version overcomes some key techniques encountered with aircraft engineering and offers some very attractive features. It can solve an optimization problem in excess of 100,000 variables. In the new version of HAJIF system, many methods such as constraint regionalization and deletion techniques are used for solution of the large-scale optimization problems.

large-scale optimization; analytical method; constraint regionalization; mathematical programming

2016-09-11

王立凯(1976—)，男，硕士研究生，高级工程师，研究方向：飞机结构优化设计及CAE软件研发。

中国航空工业集团创新基金(2013A62302R)；中国航空工业集团创新基金(2014A62340)。

V214.1

B

10.3969/j.issn.1674-3407.2016.03.024