基于Labview的轨道谱的时间历程反演程序设计

兰永霞，姜良奎

(中车青岛四方机车车辆股份有限公司工程研究中心，山东 青岛 266111)



基于Labview的轨道谱的时间历程反演程序设计

兰永霞，姜良奎

(中车青岛四方机车车辆股份有限公司工程研究中心，山东 青岛 266111)

对我国干线轨道谱、美国轨道谱、德国高低速轨道谱进行动态反演得到对应时间历程的振动信息，是车辆动力学仿真计算、整车振动台试验重要的输入激励。本文采用相位随机的三角级数法为理论基础来实现轨道谱的反演，应用Labview 编制反演程序，应用LabSQL技术管理反演数据，应用MathScript实现数据回放。充分利用了Labview虚拟仪器操作简单、界面友好的特点，有利于试验人员的操作和使用，必将为工程试验室整车振动试验技术的发展和试验能力的提升做出一定的贡献。

轨道谱；Labview；LabSQL；反演；程序设计

1 引 言

轨道不平顺是机车车辆产生振动的主要根源，是影响机车车辆动力学性能的关键因素之一。在机车车辆动力学仿真、列车综合舒适性试验和机车台架振动试验中，轨道不平顺是必不可少的激励输入[1]。为了更好地发挥工程实验室振动台的振动试验功能，实现我国干线轨道谱、美国各级轨道谱、德国高低速轨道谱以及实测谱的动态反演，配合各类仿真和试验研究的需求，设计开发了一套轨道谱反演系统。

反演系统的程序设计不仅要充分应用轨道谱反演的最新发展理论，确保反演数据的有效和精准，同时要考虑软件开发平台的交互性能与已有试验系统的兼容性能。因此，将轨道谱反演的最新发展技术——随机相位的三角级数法与Labview平台相结合[2-3]，开发一套轨道谱反演程序和软件系统，为试验能力的提升发挥重要作用。

2 轨道谱反演算法

因轨道谱的反演是车辆动力学研究、车辆动力学试验的必要输入，其反演技术得到了充分发展。目前主要有三角级数法[4]、白噪声滤波法[5]、二次滤波法[6]和反傅里叶变换法[7]。通过各种方法的研究对比，各种轨道谱反演技术得到的时域样本都正确，但是，三角级数法和反傅里叶变换法反演的样本的离散度小，而白噪声滤波和二次滤波法反演的样本离散度大[8]。同时，考虑算法的可靠性，本系统采用随机相位的三角级数法反演轨道的不平顺。

三角级数法是一种最直接轨道谱反演方法，其理论依据是任何平稳随机过程都可用一系列带随机相位的正弦函数或余弦函数的和来表示，一类是振幅和相位都随机变化，另一类是只有相位随机变化。振幅和相位都随机变化产生的随机数多，同时不能保证各态历经[8]，因此采用随机相位的三角模拟反演技术。

设轨道不平顺x(t)为各态历经随机过程，其功率谱密度函数可以通过傅里叶变换估计得到。

(1)

式中，Fx(ω,T)、Sx(ω)分别为各态历经随机过程x(t)的傅里叶变换和功率谱密度函数。

轨道不平顺随机过程可以采用复数形式的傅里叶级数表达：

(2)

式中，ω0=πT-1，T=NΔt。

式(2)的离散表达式为：

(3)

有：

(4)

(5)

(6)

据轨道不平顺是具有零均值各态历经的平稳Gauss过程的假定，将过程的傅里叶级数转化为三角级数，三角级数的叠加可以生产时程样本。轨道不平顺激励过程与相应的复傅里叶级数为一对傅里叶变换对，可表示为：

(7)

(8)

式中，Ck为复傅里叶级数展开系数；θk为随机相位角。

为描述系数Ck的随机性质，引入随机变量θk，并令其在 0～2π区间上服从均匀分布，可构造出如下轨道谱反演的轨道不平顺随机过程的三角级数表达式：

(9)

式中，ω0=π(NΔt)-1。

3 轨道谱反演的程序设计

以随机相位的三角级数法为理论基础，以Labview为软件开发平台进行轨道的反演程序设计，主要包括软件框架设计、反演界面、数据管理3个部分。

3.1 软件框架

软件采用模块化设计，总共包含3层结构：应用层、数据库层、接口层，具体如图1所示。

图1 软件架构图

3.2 数据库连接

软件的应用层实现主要功能，软件的数据库实现数据存储管理，实现软件接口层数据访问。该软件数据库选择ORACLE MySQL，该数据库是一种开源的关系型数据库管理系统。本软件使用LabSQL实现对数据库操作和访问，图2是LabSQL数据库连接和操作步骤。

图2 LabSQL连接和操作数据库步骤

3.3 轨道谱反演程序设计

在Labview中实现算法程序的实现，软件设计时，选用Labview自带的面向数学的文本化编程方式(MathScript)编写程序。在开发算法、研究处理信号理论或分析结果时，均能用MathScript方便实现。MathScript的核心是高级文本化编程语言，具有对信号处理、分析和数学计算相关任务的复杂性进行抽象化的语法和功能。本软件的算法程序设计按照上一节反演算法设计，其交互界面如图3所示。

图3 轨道谱反演参数设置交互界面

3.4 数据管理和回放

数据库管理操作包含：数据库刷新、删除、添加、波形文件数据的提取，管理和回放界面如图4所示。

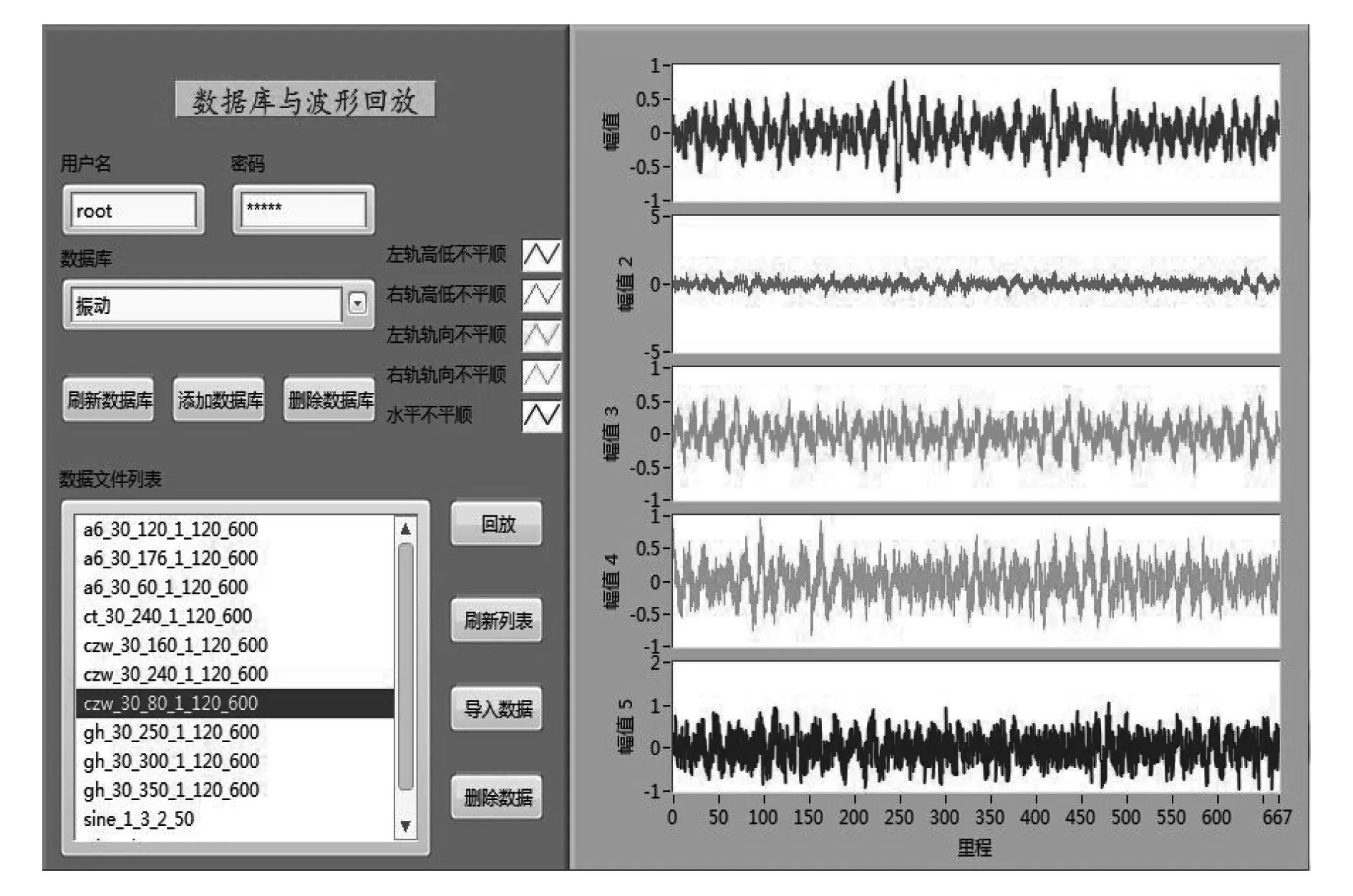
图4 数据管理和回放界面

4 轨道谱反演程序运行测试

分别选取美国轨道谱6级谱、德国低干扰轨道谱、郑武线高速试验段轨道谱，应用本文开发的软件系统进行反演，反演结果分别如图5-图7所示。

图5 美国轨道谱6级谱

图6 德国低干扰轨道谱

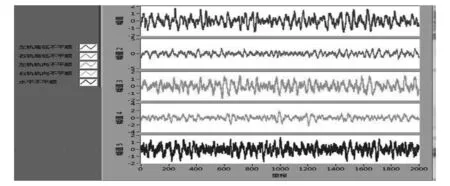
图7 郑武线高速试验段轨道谱

5 总 结

轨道谱的时间历程反演对动力性能分析、动力学试验具有重要作用，对提升试验能力具有重要意义。本文概括起来具有以下特点：

(1)将轨道谱反演技术与虚拟仪器有机结合，能实现各种轨道谱的反演、管理和回放，界面友好，便于实际应用。

(2)能够很好地兼容到试验室现有的试验平台，提高了动力学的试验能力。

[1]任尊松.车辆系统动力学[M].北京:中国铁道出版社,2007.

[2]张重雄.虚拟仪器技术-分析与设计[M].北京:电子工业出版社,2007.

[3]岂兴明,田京京,夏宁.Labview入门与实践开发100例[M].北京:电子工业出版社,2001.

[4]许昭鑫.随机振动[M].北京:高等教育出版社,1990.

[5]侯传亮,张永林.工程平稳随机过程的数值模拟研究[J].武汉工业学院学报,2003,22(3):27-29.

[6]王丰元,王颖,王东军.铁路轨道不平顺模拟的一种新方法[J].铁道学报,1997,19(6):110-115.

[7]M.L. Averill, K. David. Simulation modeling and analysis [M].New York: McGraw-Hill Book Company, 1982.

[8]刘寅华,李芾,黄运花.轨道不平顺数值模拟方法[J].交通运输工程学报,2006,6(1):29-33.

Design of Time-History Inversion Procedure for Rail Spectrum based on Labview

Lan Yongxia, Jiang Liangkui

(CRRC Qingdao Sifang Co., Ltd. National engineering Laboratory, Qingdao 266111, Shandong, China)

The time-history information of a variety of spectrums such as Chinese main line rail spectrum, American rail spectrum, Germany high-velocity and low-velocity spectrum and so on, is the important exciting input of vehicle dynamics simulation and vibration experiment of the whole vehicles. The spectrum inversion theory is the trigonometric series method with random phases. The spectrum inversion procedure is designed on the platform of Labview. The two standard tools named LabSQL and MathScript are used to manage and play back the simulation data, respectively. The main advantages of Labview virtual instrument such as operation simplification, friendly interface are beneficial to application and operation of test person. The inversion procedure will improve the experiment technique and experiment ability of the high-speed train national engineering laboratory.

rail spectrum; Labview; LabSQL; inversion; procedure design

2016-07-27

兰永霞(1970-)，女，高级工程师，主要研究方向：人机工程。

U211.3

B

10.3969/j.issn.1674-3407.2016.03.002