水下杆状结构三维振动数值模拟

刘浩宇，唐友刚，王 宾，黄 印

（1.天津大学 建筑工程学院，天津 300072；2.天津大学 水利工程仿真与安全国家重点实验室，天津300072）

水下杆状结构三维振动数值模拟

刘浩宇1，2，唐友刚1，2，王 宾1，2，黄 印1，2

（1.天津大学 建筑工程学院，天津 300072；2.天津大学 水利工程仿真与安全国家重点实验室，天津300072）

本文研究柔性杆状在涡激-参激联合作用下的三维振动响应特性问题。基于Hamilton原理，建立了柔性杆的三维振动模型，考虑 Morison力、涡激升力以及顶端变张力，对结构的涡激振动和参激-涡激联合振动进行数值模拟。针对振动方程，首先借助有限差分法和Runge-Kutta方法对方程进行数值求解，求得结构的三维振动响应，绘制了各自由度振动的时历曲线、相平面图、庞加莱截面图以及能量频谱，研究了参激-涡激联合振动情况下，杆件的非线性振动特性。

参激-涡激；耦合分析；非线性振动

引 言

细长柔性杆状结构被广泛的应用于海洋工程领域，常见的包括深海立管、TLP平台的张力腱等。对该类结构的研究中，涡激振动和参激振动尤其吸引了研究者的注意。

柔性杆在流场中，会与尾流产生相互作用，在横流方向产生涡激振动。当涡激振动频率接近柔性杆振动固有频率时，会引起大幅的谐振，即“锁定效应”，这类问题已经被广泛关注和研究［1～3］。Dong Y.Q.曾研究了波流联合作用下的张力腿涡激非线性振动［4］，并分析了涡激频率接近张力腿固有频率时，张力腿振动的稳定性问题［5］，研究表明，随着阻尼和升力系数的减小，系统趋于不稳定，结果中出现多解区域，并伴随有跳跃现象。

当柔性杆顶端边界条件发生变化时，会受到轴向动力激励，称为参数激励。Patel研究了轴向力和平台深沉同时作用下，张力腿的振动响应和稳定性问题［6，7］，研究表明在参数激励下，张力腿振动幅值增加，Mathieu不稳定区域扩大。Song.L使用频域方法研究了因轴向变张力和随机波浪力共同作用下立管的横向振动［8］，发现平台垂荡振动的频率和幅值均会对立管的波浪激励响应产生影响。

当涡激振动与参激振动同时发生时，会引起新的动力学问题［9，10］。Chatjigeorgiou建立了轴向与横向的耦合方程，将轴向振动简化为简谐参数激励，研究了横向振动的稳定性问题［11］，发现参数激励会导致立管横向振动进入耦合不稳定区域，即使加入非线性阻尼，也无法阻止参数激励引起的耦合不稳定的发生。Chatjigeorgiou针对涡激载荷频率是横向一阶固有频率的二倍，使用多尺度方法以及数值解法两种算法求解模型［12］，研究了一次和二次阻尼成分的影响。

目前针对细长柔性杆状结构的研究，大都使用单自由度模型，将边界运动以及顶张力简化为简谐参数项加在柔性杆横向振动方程中，不考虑柔性杆的轴向和迎流向振动随时间的变化。而事实上，柔性杆状结构由于轴向刚度较低，其轴向振动不可忽略［13，14］。本文基于 Han等［15］的工作，建立了细长柔性杆状结构三维振动方程，研究了顶端参数激励对结构振动幅值、振动状态的影响和非线性特性，并开展实验对理论计算结果进行了验证。

1 理论模型推导

本文采用 Han提出的理论模型［15］，并针对工程实际进行修改，如图1所示：将柔性杆等效为柔性等截面梁，长度为 L。柔性杆顶端受到x方向张力NT=N0+N，用于模拟参激作用，柔性杆底端与海底铰接。

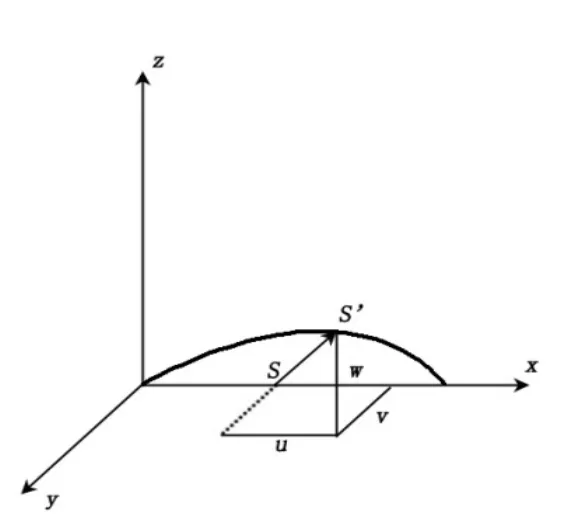
图1 柔性杆理论模型

得到振动方程：

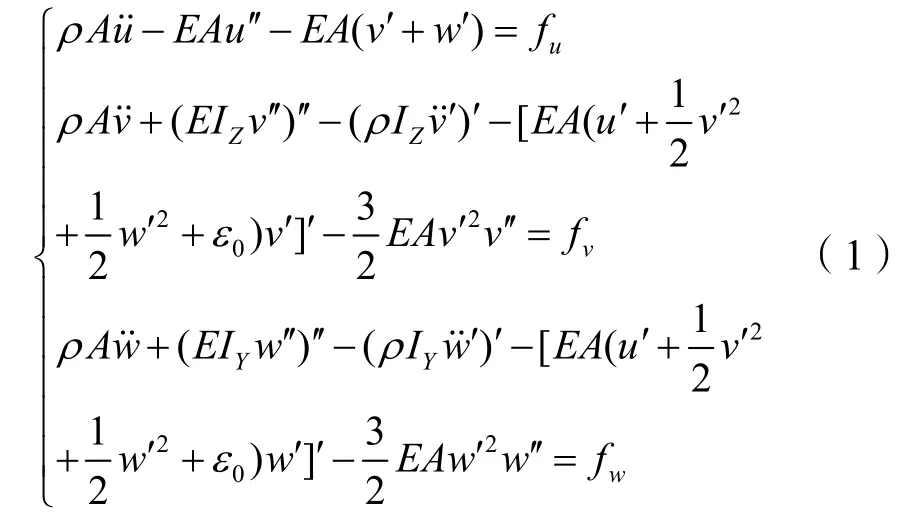
式中：ρ为柔性杆密度；A为横截面面积；IZ和IY为惯性矩；EA为轴向刚度；EI为弯曲刚度；u..为u对时间t的二次导数；u＇、u＇＇和u＇＇＇＇为u对杆长l的一次、二次和四次导数。

满足的边界条件如下：

式中：N0为预张力，相应的预应变用0ε表示；N为动张力。

本文采用有限差分法将式（3）在空间上离散，得到对时间 t的常微分方程组，考虑边界条件式（2）～（6），利用4阶Runge-Kutta法求解振动响应。

2 算例分析

本文算例如图 2，该图为杆件受力示意，流场沿y轴负方向，流速为U；重力沿z轴负方向，顶端受到动张力NT。

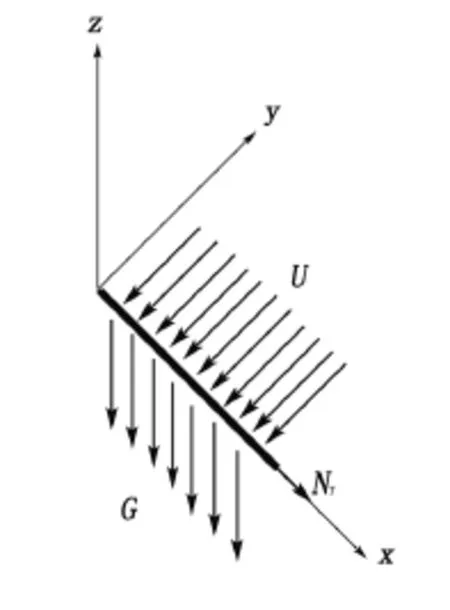
图2 柔性杆受力示意

采用Morison方程来表示流场在y方向产生的非线性力：

柔性杆z向的涡激升力：

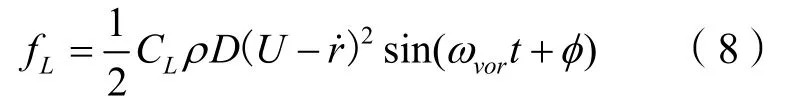
式中：CL为涡激升力系数，这里取0.3；ωvor为涡泄频率，满足，St为斯特罗哈尔数，取0.2；φ取180°。

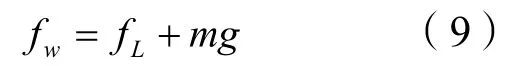
柔性杆x向不受到沿管长方向的分布力，有：

杆件参数见表1。

表1 柔性杆参数

表1中：Nc为参激力幅值；f为参激频率。

计算工况如表2，共5组。

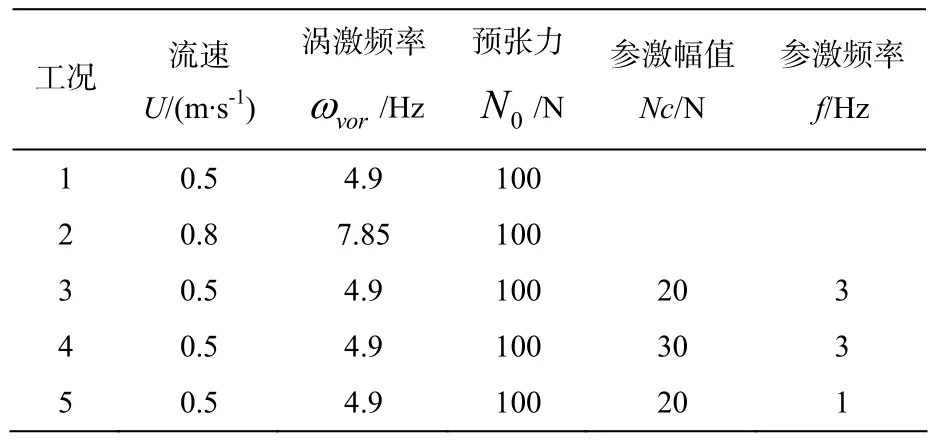
表2 实验和计算工况

工况1和2不包含参数激励，通过对两个结果的对比，研究流速对涡激振动的影响。需要注意的是，流速为0.5 m/s时，涡激频率接近模型z向振动的固有频率，所以该流速下，柔性杆受“锁定”效应影响。工况 3在工况 1的基础上，增加参数激励，通过两者的对比，可以得到参激作用对柔性杆涡激振动的影响。而工况4和5针对工况3分别改变了参激幅值和参激频率，用以研究两个参数的变化对参激-涡激联合振动的影响。

2.1 流速对柔性杆涡激振动的影响

根据数值模拟，预张力100 N，流速0.5 m/s与0.8 m/s下，柔性杆中点涡激力方向（z向）位移时历曲线如图 3。从图中可以看到，流速为 0.5 m/s时，柔性杆在“锁定”效应影响下，中点位移较大，且表现出单频振动特性，2倍频成分不明显，而在流速0.8 m/s下，两个频率成分均凸显。

图3 涡激z向时历曲线（NT=N0，U=0.5 m/s和U=0.8 m/s）

柔性杆中点涡激z向位移能量频谱如图4。从图4（a）中可以看到，流速为0.5 m/s时，结构振动能量在时存在峰值，该频率振动由涡激力引起。在处同样出现峰值，这是由于柔性杆振动方程中包含二次非线性，导致振动响应出现倍频成分。图4（b）中，流速为 0.8 m/s，结构振动能量在及时存在峰值，说明随着流速的增加、结构涡激振动不再被“锁定”，结构仍对涡激激励产生倍频响应。

另外，对比图4（a）和图4（b）还可以发现，流速为0.5 m/s时，两个峰值相差较大，这说明由于“锁定”效应的存在，能量成分中涡激振动占主要地位。流速增大到 0.8 m/s时，振动脱离“锁定”区域，能量谱中两个峰值极为相近，说明“锁定”效应不再明显时，结构表现出强非线性，倍频响应不可忽略。

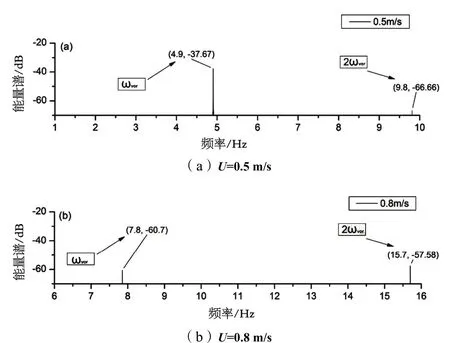
图4 中点z向位移能量频谱

各振动成分能量峰值随流速的变化曲线如图5。从图中可以看到，流速处于0.2 m/s到0.7 m/s之间时，涡激振动能量峰值较大，说明该流速范围属于“锁定”区域。注意到，倍频激励也存在类似的“2倍频锁定”区域（0.3～0.5 m/s），在该区域内，柔性杆涡激振动占主要作用，2倍频振动可以忽略，流速离开这个区域后，2倍频成分作用凸显，其影响不可忽略。

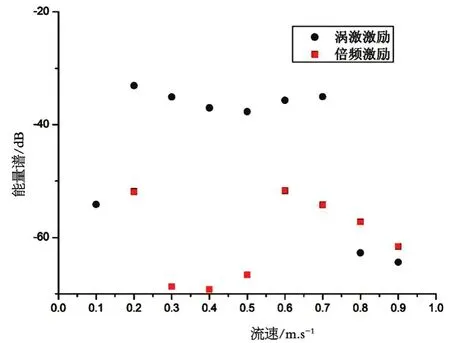
图5 能量峰值随参激频率变化曲线

2.2 参激力对柔性杆涡激振动的影响

预张力100 N，流速0.5 m/s，有/无轴向参数激励情况下，柔性杆中点涡激z向位移时历曲线如图6，存在参数激励时，振动幅值有所增加。

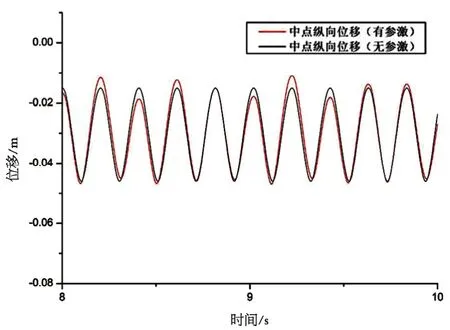
图6 中点位移时历曲线

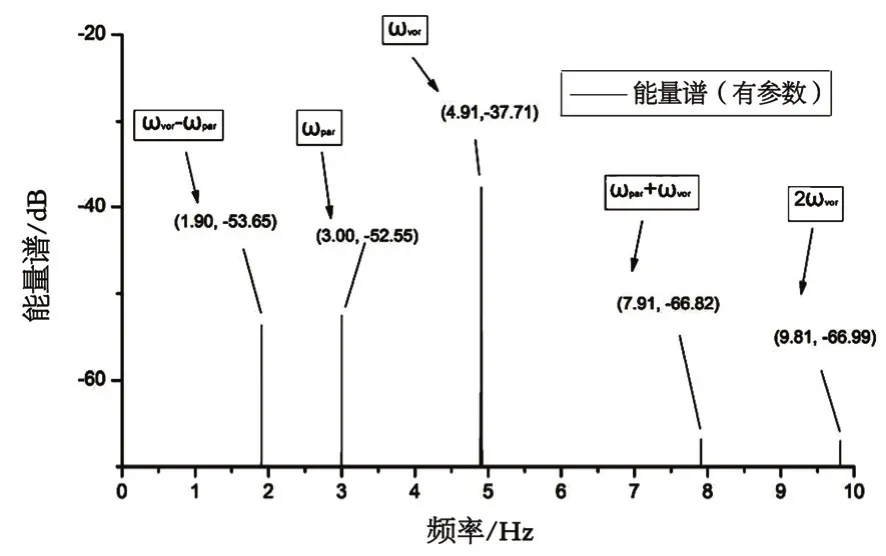
图7 中点z向位移能量频谱

流速0.5 m/s，顶端轴向张力为NT=20cos（2π×3t）+N0，柔性杆中点涡激z向位移能量频谱如图 7。从图中可以看到，能量谱存在多个频率成分：位移能量谱在和时存在幅值，说明柔性杆对涡激激励产生涡激响应和二倍频响应；位移能量谱在处存在峰值，该频率恰好为参激频率，说明该成分振动是由参数激励引起。

2.3 参激幅值和频率对柔性杆涡激振动的影响

预张力100 N，流速0.5 m/s，不同参激频率和不同参激幅值下，柔性杆中点涡激z向位移时历曲线如图8。从图8（a）中可以看到，不同参激频率下，振动位移均为0.036 m，变化不大。图8（b）中可以看到，随着参激幅值的增加，z向振幅随着增加。

图8 中点应力时历曲线

预张力100 N，流速0.5 m/s，参激频率1 Hz（顶端张力NT=20cos（2πt×1）+N0）和参激幅值30 N（顶端张力NT=30cos（2πt×3）+N0）情况下，柔性杆中点涡激z向能量频谱如图9。从图中可以看到，参激频率和幅值发生改变后，柔性杆仍存在着倍频响应和组合谐振。

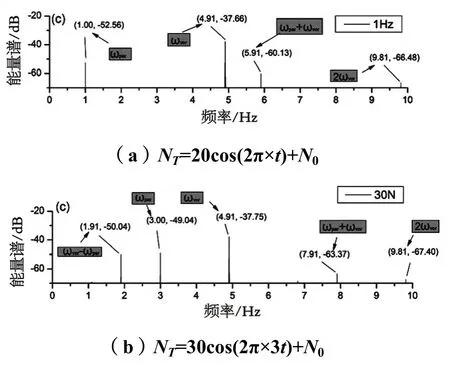
图9 中点z向位移能量频谱

预张力100 N，流速0.5 m/s，在不同参激频率下（顶端张力NT=20cos（2πt×variable）+N0），各振动成分能量峰值随频率变化曲线如图10。从图中可以看到，涡激激励和2倍频激励的幅值随参激频率改变很小。其他各振动成分的能量峰值随参激频率发生变化，参数激励和组合激励，尤其是和频激励，仅存在于低频范围内，当参激频率增大到8 Hz后，与参激相关的各振动成分不再起作用。

图10 能量峰值随参激频率变化曲线

预张力100 N，流速0.5 m/s，在不同参激幅值下（顶端张力NT=variable×cos（2πt×3）+N0），各振动成分能量峰值随参激幅值变化曲线如图11。从图中可以看到，涡激激励和2倍频激励的幅值随参激幅值改变很小。其他各振动成分的能量峰值随参激幅值发生变化，参数激励和组合激励，随着参数激励幅值的增大而增大，当参激幅值达到 3 N时，参数激励成分凸显，差频激励在参激幅值为4 N时出现，而和频激励在参激幅值达到15 N时才出现。

图11 能量峰值随参激频率变化曲线

3 结 论

本文分析了柔性杆涡激振动性特性，以及参数激励对涡激振动的影响。针对不同的参数影响，设计了5组工况，分别计算了每组工况下，柔性杆模型中点应变的时历曲线，并求取了其能量频谱。通过不同工况下应变幅值以及能量谱峰的相互对比，研究了流速、参激频率和幅值对柔性杆涡激振动幅值和振动特性的影响。研究表明：

1）由于结构的非线性，柔性杆会在对涡激力产生2倍频响应。

2）当涡激频率接近柔性杆z向固有频率时，柔性杆发生涡激共振。当流速增加，涡激频率增大后，涡激频率离开“锁定”区域时，柔性杆振幅减小，倍频响应效应更加明显。

3）顶端简谐参数激励会引起柔性杆振幅的增加，且振幅随着参激幅值的增加而增加。

4）参数激励幅值和频率的改变，对涡激振动和2倍频振动影响不大。

5）柔性杆同时受到参数激励和涡激力作用时，涡激力和参激力会以组合的形式，激发柔性杆的和频和差频响应。

6）和频和差频振动仅在参数激励达到一定强度时才出现，本实验中，差频振动在参激幅值达到预张力的 4 %时会出现，而和频振动需要达到15 %，随着参数激励幅值的增加，参激振动、和频振动和差频振动逐渐增强。

7）和频和差频振动仅在低频的参数激励时出现，本实验中，只有参激频率小于3 Hz时，才存在和频振动，小于6 Hz时，存在差频振动。

［1］Williamson C H K，Govardhan R.Vortex-Induced Vibrations［J］.Annual Review of Fluid Mechanics，2004，36（1）：413-455.

［2］Gabbai R D，Benaroya H.An overview of modeling and experiments of vortex-induced vibration of circular cylinders［J］.Journal of Sound and Vibration，2005，282（3-5）：575-616.

［3］Bearman P W.Circular cylinder wakes and vortex-induced vibrations［J］.Journal of Fluids and Structures，2011，27（5-6）：648-658.

［4］Dong Y，Lou J.Vortex-induced nonlinear oscillation of tension leg platform tethers［J］.Ocean engineering，1991，18（5）：451-464.

［5］Dong Y，Xie G，Lou J.Stability of vortex-induced oscillations of tension leg platform tethers［J］.Ocean engineering，1992，19（6）：555-571.

［6］Patel M H，Park H I.Combined axial and lateral responses of tensioned buoyant platform tethers［J］.Engineering Structures，1995，17（10）：687-695.

［7］Patel M H，Park H I.Dynamics of tension leg platform tethers at low tension.Part I-Mathieu stability at large parameters［J］.Marine structures，1991，4（3）：257-273.

［8］Lei S，Zhang W，Lin J，et al.Frequency domain response of a parametrically excited riser under random wave forces［J］.Journal of Sound and Vibration，2014，333（2）：485-498.

［9］Park H，Jung D.A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations［J］.Ocean Engineering，2002，29（11）：1313-1325.

［10］Kuiper G L，Brugmans J，Metrikine A V.Destabilization of deep-water risers by a heaving platform［J］.Journal of Sound and Vibration，2008，310（3）：541-557.

［11］Chatjigeorgiou I K，Mavrakos S A.Bounded and unbounded coupled transverse response of parametrically excited vertical marine risers and tensioned cable legs for marine applications［J］.Applied Ocean Research，2002，24（6）：341-354.

［12］Chatjigeorgiou I K，Mavrakos S A.Nonlinear resonances of parametrically excited risers—numerical and analytic investigation for Ω=2ω1［J］.Computers & Structures，2005，83（8-9）：560-573.

［13］于清，洪嘉振.柔性多体系统动力学的若干热点问题［J］.力学进展，1999，29（2）：145-154.

［14］瞿元，余春华，尹晓春.横向有限应变对部分浸入水中平面运动柔性梁的非线性振动响应的影响［J］.工程力学，2007，24（2）：188-192.

［15］Han S M，Benaroya H.Vibration of A Compliant Tower in Three-Dimensions［J］.Journal of Sound and Vibration，2002，250（4）：675-709.

3D Vibration Numerical Simulation of Underwater Rod Structure

Liu Haoyu1，2，Tang Yougang1，2，Wang Bin1，2，Huang Yin1，2
（1.School of Civil Engineering，Tianjin University，Tianjin 300072，China； 2.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China）

To study 3D vibration response characteristics of flexible rod structure under parametric and vortex-induced excitation，a 3D vibration model of flexible rod is built on the basis of Hamilton principle，which takes into account Morison force，vortex-induced lifting force and top variable tension，and simulate the vortex-induced vibration with and without parametric excitation.The vibration equation is solved by using finite difference method and Runge-Kutta method，then 3D vibration response results are used to draw the time history curves responding multi-degrees of freedom vibration，phase plane diagrams，Poincare section map and energy spectrum.In addition，special attention is paid to the nonlinear vibrating characteristic of rod structure under parametric and vortex-induced excitation.

parametric and vortex-induced excitation； coupling analysis； nonlinear vibration

U661.43

A

1004-9592（2016）05-0005-06

10.16403/j.cnki.ggjs20160502

2015-12-07

刘浩宇（1990-），男，硕士，主要从事平台水动力研究。