基于模糊聚类的含风电场发电系统可靠性分析
2016-11-10刘步中张曦煌
刘步中,张曦煌
(1.江苏省中小企业电子产品工程技术研发中心,江苏淮安 223003;2.江南大学信息工程学院,江苏无锡 214000)
基于模糊聚类的含风电场发电系统可靠性分析
刘步中1,张曦煌2
(1.江苏省中小企业电子产品工程技术研发中心,江苏淮安223003;2.江南大学信息工程学院,江苏无锡214000)
风电出力的随机性和间歇性使得风电在接入发电系统时会对发电系统可靠性造成影响。考虑到风电出力与负荷之间存在一定的相关性,提出了一种基于模糊聚类的风电场多状态可靠性模型。模型根据风电场出力与负荷数据的分布情况,使用两维模糊聚类对数据进行状态划分,并计算各状态之间的转移概率,最后通过序贯蒙特卡罗模拟对含风电场发电系统进行可靠性评估。算例分析结果表明,所建模型能够很好地模拟出风电场出力和负荷的分时序列,且可靠性分析结果准确有效。
风电场;模糊聚类;相关性分析;可靠性分析
可再生能源的大规模利用对现代社会的节能减排和可持续发展至关重要。截至2015年底,全球风电装机容量432.4 GW,其中我国风电装机容量145.1 GW,累计风电装机容量世界第一。在各项扶持可再生能源发展政策的推动下,我国风电产业发展迅猛[1-2]。
因风电场出力具有很强的间歇性和随机性,需建立合理准确的模型来分析含风电场发电系统的可靠性。可靠性分析常用方法主要有解析法与蒙特卡罗模拟法[3-6]。其中,蒙特卡罗模拟法更加适用于复杂的控制和不确定的负荷特性等场景。国内外学者对风电场可靠性模型做了许多研究[7-9],建立了风电场多状态可靠性模型。
本文采用两维模糊C均值聚类(Fuzzy c-means,FCM)对风电场进行多状态划分,建立了基于模糊聚类的风电场多状态可靠性模型,并基于我国西部某地区风电场实测数据计算风电场各状态之间的转移概率,以RBTS测试系统为算例,通过序贯蒙特卡罗模拟仿真对含风电场发电系统进行可靠性评估。
1 风电出力与负荷相关性分析
1.1相关性测度
描述随机变量间相关关系的参数主要有Pearson线性相关系数、Kendall秩相关系数、Spearman秩相关系数等。与Pearson线性相关系数相比,Kendall秩相关系数和Spearman秩相关系数的优点主要体现在其稳健性、单调增变换不变性和对更广的相关关系的描述上[10],因而更适合用来处理风电出力与负荷间的非线性相关关系,文中选取了Kendall秩相关系数作为衡量变量间相关性的工具[11]。
设(x1,y1)和(x2,y2)为随机向量(X,Y)的两组观测值,若x1<x2且y1<y2,或者x1>x2且y1>y2,既(x1-x2)(y1-y2)>0,则称(x1,y1)与(x2,y2)是一致的,如果(x1-x2)(y1-y2)<0,则称(x1,y1)与(x2,y2)是不一致的。
(X,Y)是一个具有N组观测值的随机向量,则存在C2N个两两组合,其中每个组合可能相互一致,也可能是不一致的,即,c为其中的一致组合数量,d为不一致组合数量,定义样本 {(x1,y1),(x2,y2),…,(xN,yN)}的Kendall秩相关系数为τ=(c-d)/C2N,τ代表了2个随机向量一致的概率与不一致的概率的差值。Kendall秩相关系数可由下式来定义:
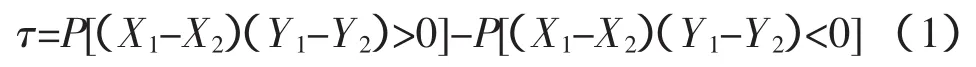
式中:(X1-X2)和(Y1-Y2)之间相互独立,且该随机向量与(X,Y)具有相同的分布。
根据以上对Kendall秩相关系数的阐述,变量τ代表的2个随机向量之间的相关程度具有如下特征:
1)|τ|≤1,|τ|越接近1,表明向量间的相关性越高。
2)当τ>0时,表明向量间的变化趋势相同,两者之间呈现正相关。
3)当τ<0时,表明向量间的变化趋势相反,两者之间呈现负相关。
4)当τ=0时,表明向量间的相关程度不确定,无法描述。
1.2风电出力与负荷相关性分析
使用Kendall相关系数分析风电出力与负荷之间的相关程度,首先定性分析风电与负荷的相关性。我国西部某地区某日风电出力与典型日负荷曲线的变化趋势如图1所示。
由图1可以看出,风电出力在部分时段与负荷的波动呈相反的变化趋势,即风电呈现反调峰特性。随着风电穿透功率的增大,风电并网会对电力系统的调峰产生影响。
以上对图1做了定性分析。下文将对1~12月的风电出力与负荷数据进行随机抽样,随机抽取48天,计算其Kendall秩相关系数,以Kendall秩相关系数作为量化指标,计算风电与负荷的相关性,对以上情况进行定量分析,结果见表1。
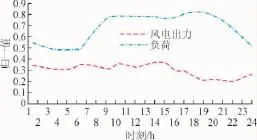
图1 风电出力与负荷的变化特性对比Fig.1 Comparison of the variation characteristics of wind power output and load
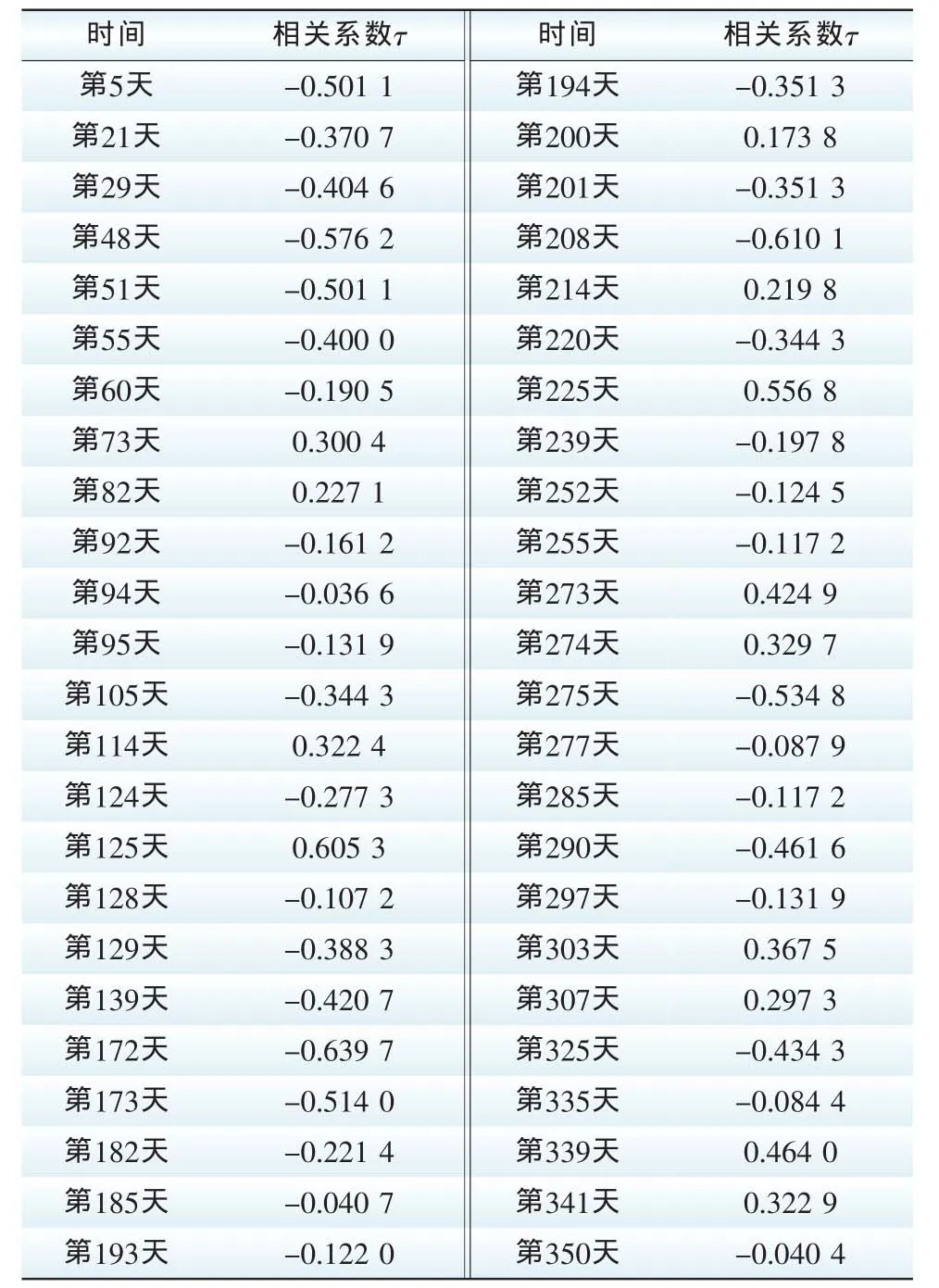
表1 风电出力与负荷的相关性Tab.1 Correlation between wind power output and load
由表1可以看出,随机抽取的48天中,风电基本都呈现反调节特性,即风电出力与负荷存在负相关性,风电场的接入给电网调峰带来消极的影响。
2 聚类理论及风电场可靠性建模
2.1FCM算法及步骤
FCM算法的目标是将n个向量xi(i=1,2,…,n)划分到c个模糊组中去,同时计算得出每个组的聚类中心,以达到使价值函数最小的目的。由于归一化的要求,一个数据集合的隶属度总和为1:

那么,FCM的价值函数(或目标函数)为:
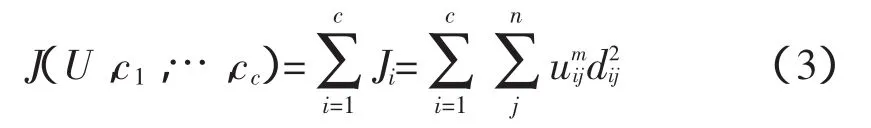
这里uij介于(0,1)间;ci为模糊组I的聚类中心,dij=||ci-g||为第I个聚类中心与第j个数据点间的欧几里德距离;且m∈[1,∞)是一个加权指数。
构造如下新的目标函数,可求得使式(3)达到最小值的必要条件:

这里λj,j=1到n,是式(2)的n个约束式的拉格朗日乘子。对所有输入参量求导,使式(3)达到最小的必要条件为:

根据以上2个必要条件,FCM聚类算法的过程并不复杂,只是一个简单的不断迭代的过程。通过批处理的方式运行,FCM聚类算法确定聚类中心ci和隶属矩阵U的方法如下。
步骤1:初始化隶属度矩阵U,取值由(0,1)间随机生成,使U满足式(2)中的约束条件。
步骤2:根据式(5)计算得到c个聚类中心ci,i= 1,2,3,…,c。
步骤3:根据式(2)计算得出价值函数。若计算结果小于某个确定的阀值,或是价值函数的值与上次计算结果相比,其改变量小于某个阀值,则可以将算法停止。
步骤4:根据式(6)计算得到新的U矩阵。返回步骤2)。
2.2状态转移模型
通过FCM聚类将风电场出力划分为M个区域,并计算出各个区域转移的概率。
若风电场出力此时落在区域i,则下一时刻风电场出力可能出现的区域为M个(包含此时所处的区域i),到达区域j的概率Pij为:
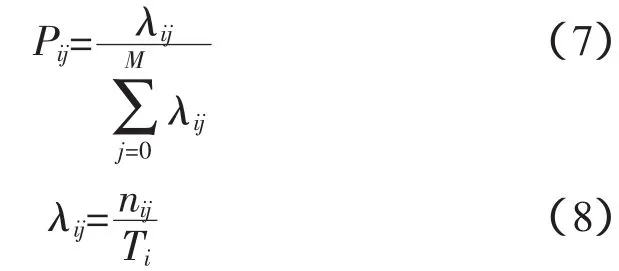
式中:λij为区域i到区域j的转移率nij为从区域i到区域j的转换次数;Ti为处于区域i的总时间。很显然:

3 蒙特卡罗模拟仿真
根据FCM聚类理论建立含风电出力发电系统可靠性模型,在此基础上,考虑传统发电机组随机故障对可靠性计算的影响,基于蒙特卡罗模拟对发电系统进行可靠性评估。大致流程分为以下几个步骤:
1)根据FCM聚类结果,基于状态转移获取模拟期限内风电出力及负荷数据。
2)获取模拟期限内传统机组的发电容量数据。首先构建传统发电机组的停运模型,然后对模型进行取样,获取传统发电机组每个小时的停运状况,最后根据机组停运表得到在模拟期限内的传统机组出力数据。
3)计算相关可靠性指标。根据步骤1)和步骤2)得到的数据对发电系统的状态进行判别,计算最常用的2个可靠性指标:失负荷时间期望(loss of load expectation,LOLE)指可靠性分析过程中系统不能满足负荷需求的总小时数的数学期望值;电量不足期望(loss of energy expectation,LOEE)指可靠性分析过程中系统发电容量不足导致负荷需求电量削减的期望数值。
4 算例分析
本文选取我国某地区风电场出力及负荷实测数据为数据样本,基于RBTS可靠性测试系统进行可靠性分析。文中数据聚类数定为60。可靠性测试系统中传统发电机组的台数为11,其总装机容量为240 MW,系统最高负荷为205 MW。在不含风电场出力时,根据地区历史负荷数据计算得到系统可靠性指标LOLE为5.456 h/a,LOEE为42.489 MW/a。
4.1FCM聚类建模
根据聚类数对样本数据进行聚类,计算得到每个聚类中心的坐标,聚类结果如表2和图2所示。
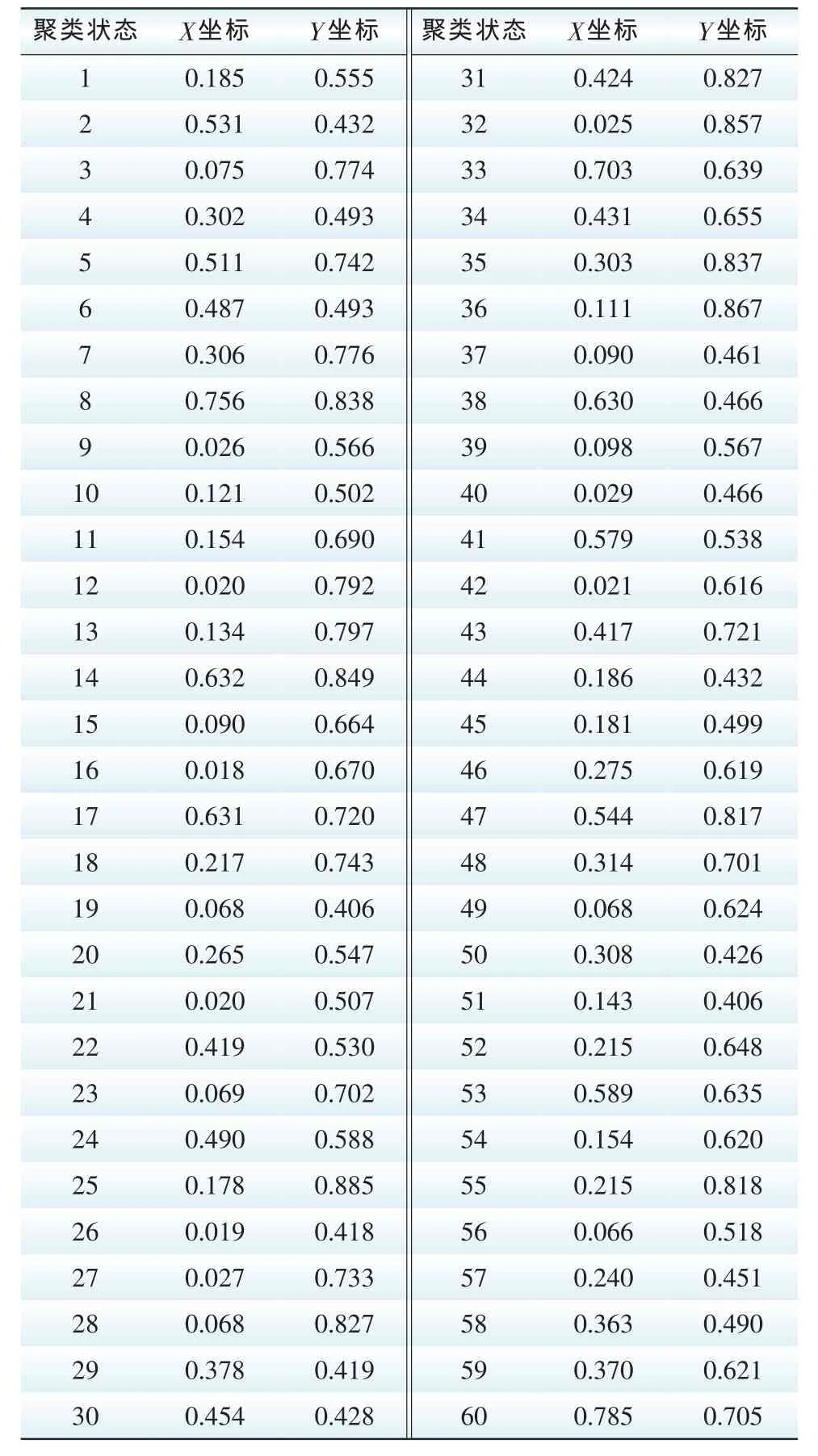
表2 聚类中心坐标Tab.2 Cluster center coordinates
图2中每个黑色轮廓线内区域代表一个类,红色十字点代表聚类中心,以此作为风电出力与负荷大小序列的基础。
4.2可靠性指标计算
将系统中强迫停运率为0.02的40 MW传统发电机组替换为40 MW风电场时,根据实际风电场出力和负荷数据计算得到的LOLE上升至37.527 h/a,LOEE值上升至426.055 MW/a。以此计算结果作为参考值,根据本文建立的FCM聚类模型,基于蒙特卡罗模拟计算在40 MW传统机组被替换为风电场出力时的可靠性指标。得到的结果如表3所示。

图2 聚类散点图Fig.2 Scatter plot
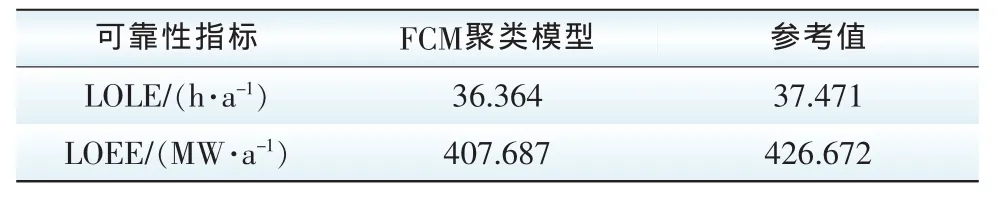
表3 可靠性指标Tab.3 Reliability index
通过比较,使用FCM聚类模型计算得出的结果与实际参考值很接近,以此验证了模型的准确性。
为进一步分析本文提出的FCM聚类模型在进行可靠性计算时的表现,在保证11台传统发电机组容量不变的情况下,不断增加风电场容量,观察可靠性计算结果,可靠性指标LOLE和LOEE值随风电场容量增加的变化情况如图3和图4所示。

图3 LOLE值随风电容量变化Fig.3 LOLE value changes with wind power
分析图3与图4可以得出,在保持传统机组容量不变的情况下,光伏电站容量的增加使得发电系统可靠性得到明显提高,主要原因在于电源容量的增加。当风电场容量达到100 MW时,可靠性指标LOLE降至1.423 h/a,LOEE值降至14.451 MW/a。当风电场容量继续增加时,可靠性指标LOLE和LOEE的下降趋势趋于平缓,表现出一定的饱和特性。
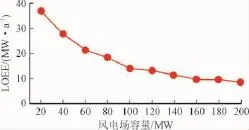
图4 LOEE值随风电容量变化Fig.4 LOEE value changes with wind power
本文提出的FCM聚类模型考虑了风电场出力与负荷的相关性对发电系统可靠性的影响,其计算结果真实有效。
5 结语
依据我国某地区风电场实测出力及负荷数据,在应用FCM聚类算法的基础上建立了风电出力及负荷的可靠性模型,基于RBTS可靠性测试系统对含风电出力发电系统进行了可靠性分析,得出如下结论。
1)研究了风电出力与地区电网负荷的相关性。结果表明,风电具有反调特性,风电场的接入给电网调峰带来消极的影响。
2)根据本文建立的FCM聚类可靠性模型,基于RBTS测试系统对含风电出力发电系统进行了可靠性分析,验证了模型的有效性。
[1]BP.Statistical review of world energy[R].England:British Petrol.
[2]Global Wind Energy Council(GWEC).Global wind statistics 2014[R/OL].Brussels:GWEC,2015[2015.2.28].http://www.gwec.net/wp-content/uploads/2015/02/GWEC_Global WindStats2014_FINAL_10.2.2015.pdf.
[3]ZHANG P,WANG Y,XIAO W D,et al.Reliability evaluation of grid-connected photovoltaic power system[J].IEEE Transactions on Sustainable Energy,2012,3(3):379-389.
[4]赵渊,谢开贵.电网可靠性指标概率密度分布的解析计算模型[J].中国电机工程学报,2011,31(4):31-38.ZHAO Yuan,XIE Kaigui.Analytical calculation model of reliability index probability density distribution of power grid[J].Chinese Journal of Electrical Engineering,2011,31(4):31-38(in Chinese).
[5]张硕,李庚银,周明.含风电场的发输电系统可靠性评估[J].中国电机工程报,2010,30(7):8-14.ZHANG Shou,LI Gengyin,ZHOU Ming.Reliability assessment of generation and transmission system with wind farm[J].China Electrical Engineering,2010,30(7):8-14(in Chinese).
[6]黄海煜,于文娟.考虑风电出力概率分布的电力系统可靠性评估[J].电网技术,2013(9):2585-2591.HUANG Haiyu,YU Wenjuan.Reliability evaluation of power system considering wind power output probability distribution[J].Power Grid Technology,2013(9):2585-2591(in Chinese).
[7]吴义纯,丁明,李生虎.风电场对发输电系统可靠性影响的评估[J].电工技术学报,2004,19(11):72-77.WU Yicun,DING Ming,LI Shenghu.Evaluation of the effect of wind farm on the reliability of the power transmission system[J].Transactions of China Electrotechnical Society,2004,19(11):72-77(in Chinese).
[8]WANG P,BILLINTON R.Time-sequential simulation technique for rural distribution system reliability cost/worth evaluation including wind generation as alternative supply[J].Generation,Transmission and Distribution,IEE Proceedings,2001,148(4):355-360.
[9]吴林伟,张建华,刘若溪.考虑风电机组故障的风电场可靠性模型及其应用[J].电力系统自动化,2012,36(16):31-35.WU Linwei,ZHANG Jianhua,LIU Ruoxi.Reliability model of wind farm considering fault of wind turbine and its application[J].Automation of Electric Power System,2012,36(16):31-35(in Chinese).
[10]PARZEN E.On estimation of a probability density function and mode[J].Annuals of Mathematical Statistics,1962,33(3):1065-1076.
[11]郭春杰,袁越.电网故障下直驱永磁风力发电机的无功功率控制策略[J].电网与清洁能源,2012,28(9):73-78.GUO Cunjie,YUAN Yue.Reactive power control strategy of direct driven permanent magnet wind power generator under grid fault[J].Power System and Clean Energy,2012,28(9):73-78.(in Chinese).
(编辑徐花荣)
Reliability Analysis of Generation Systems With Wind Power Based on Fuzzy Clustering
LIU Buzhong1,ZHANG Xihuang2
(1.Small and Medium Enterprises Electronic Products Engineering Technology Research Center in Jiangsu Province,Huaian 223003 Jiangsu,China;2.College of Information Engineering,Jiangnan University,Wuxi 214000,Jiangsu,China)
The randomness and intermittent of wind power output will affect the reliability of the power generation system when the wind power is connected to the power generation system.Considering the correlation between wind power output and load,a multi-state reliability model of wind farm based on fuzzy clustering is proposed in this paper.Model based on wind farm output and the distribution of load data,using a two dimensional fuzzy clustering to divide the state of data,and calculate the transition probabilities between the States.Finally,through sequential Monte Carlo simulation of wind power generation system reliability assessment.The numerical example shows that the proposed model can simulate the time series of wind farm output and load,and the reliability analysis results are more accurate.
wind farm;fuzzy clustering;correlation analysis;reliability analysis
1674-3814(2016)07-0138-05
TM615
A
江苏省产学研合作项目(BY2015019-30);淮安市科技计划社会发展项目(HAS2015016);淮安市光电池及LED技术重点实验室项目(HAP0912)。
Research cooperation project of Jiangsu Province(BY2015019-30);Social development project of Huaian science and technology project(HAS2015016);Huaian Key Laboratory of optical battery and LED Technology(HAP0912).
2016-04-08。
刘步中(1982—),男,硕士,讲师/工程师,研究方向为嵌入式系统技术,新能源技术;
张曦煌(1962—),男,博士,教授,硕士生导师,研究方向为嵌入式系统、新能源技术、无线网络。
