分布式光伏集群谐振分布范围及其影响因素分析
2016-11-10高静李鹏孙健
高静,李鹏,孙健
(1.新能源电力系统国家重点实验室(华北电力大学),河北保定 071003;2.国网北京市电力公司电力科学研究院,北京 100075)
分布式光伏集群谐振分布范围及其影响因素分析
高静1,李鹏1,孙健2
(1.新能源电力系统国家重点实验室(华北电力大学),河北保定071003;2.国网北京市电力公司电力科学研究院,北京100075)
分布式光伏集群并网系统中,由于光伏并网台数的增多,使得系统成为一个高阶LC网络,谐振频率分布更加复杂。根据分布式光伏集群并网系统的结构,研究了二阶LC网络和高阶LC网络的谐振分析,得到逆变器自身、其他并联逆变器以及电网之间存在复杂的谐振耦合关系,并确定了分布式光伏集群并网谐振频率的分布范围。在谐振耦合关系的基础上,分别研究了电网阻抗和滤波电容参数、并联逆变器台数以及系统网架结构变化对谐振频率的影响。仿真结果表明以上因素都会引起分布式光伏集群谐振频率的变化。
分布式光伏;集群并网;谐振频率分布范围;谐振影响因素
随着能源枯竭和环境问题的日益加剧,传统的化石燃料已经无法满足生产的要求[1-2]。同时,可再生能源由于具有储量丰富、清洁无污染等多方面的优点得到了广泛关注[3-4]。随着风电、光伏等可再生能源的应用越来越普遍,分布式能源(distributed generation)在电网中的渗透率不断增加[5]。分布式光伏集群并网系统中由于并联逆变器数量的大幅度增加,系统成为一个高阶LC网络,固有谐振点发生了变化,谐振耦合关系更加复杂。
分布式光伏通过逆变器集群并网会引起系统发生多重电能质量问题,如:电压与电流谐波、电压暂降、电压突升、电压短时中断、电压波动与闪变、电压与电流不平衡分量、谐振等等[6-7]。此外,由于光伏输出功率的波动性以及电力电子装置的大量使用,分布式光伏集群并网系统中谐波成分更加复杂,引起系统谐振现象的可能性大大提高。
分布式光伏集群并网系统中通过滤波器连接逆变器的交流输出侧和电网[8-9]。在分布式光伏集群并网系统中多采用LCL滤波器,其具有更好的高频电流纹波抑制效果[10-11]。但LCL滤波器自身存在着谐振问题,因此为了提升LCL滤波器的应用性能,需要对其谐振频率分布范围进行分析[12-13]。分布式集群并网系统中由于并联逆变器的增加,系统谐振问题较传统的单逆变器并网更加复杂。因此,为了保证分布式光伏集群并网系统安全稳定运行,抑制谐振现象,需要对谐振分布范围进行分析,并确定各个影响因素对谐振产生的影响。
本文针对分布式光伏集群谐振问题,研究了二阶LC网络和高阶LC网络谐振特性,分析了谐振频率的分布范围。在此基础上,分析了电网阻抗和滤波电容参数、并联逆变器台数以及系统网架结构变化对谐振频率分布的影响,并通过仿真验证了理论分析的正确性。
1 谐振频率分布范围分析
分布式光伏集群并网系统如图1所示,Us为电网电压;Lli为线路阻抗;LTi为升压变压器阻抗;UPVi则表示光伏集群系统。以下就二阶LC网络和高阶LC网络分别进行谐振分析。分布式光伏集群并网系统参数如表1所示。
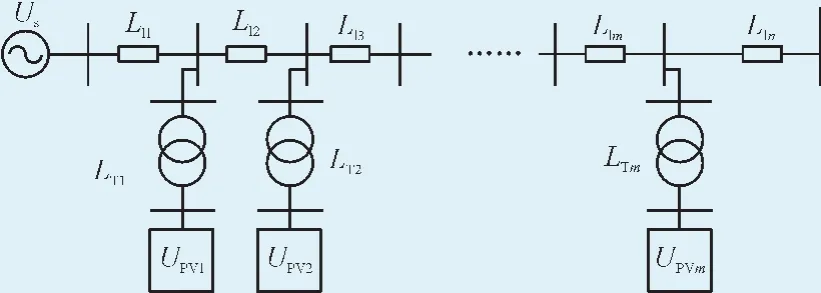
图1 分布式光伏集群并网系统Fig.1 Clustered distributed grid-connected PV system
1.1二阶LC网络谐振分析
并网逆变器结构图如图2所示,单逆变器控制系统如图3所示[14]。

图2 并网逆变器结构图Fig.2 Grid-connected inverter structure

图3 单逆变器控制系统Fig.3 Single inverter control system
根据图3可得系统传递函数如下:

式(1)中传递函数PiL1的Bode图如图4所示。可以看出,单逆变器的并网输出电流存在单个谐振点,谐振频率为610 Hz。
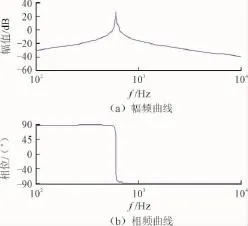
图4 单台逆变器并网PiL1的Bode图Fig.4 Bode of single grid-connected inverter PiL1
1.2高阶LC网络谐振分析
集群并网逆变器结构图如图5所示,谐振分析电路如图6所示[15]。

图5 集群并网逆变器结构图Fig.5 Structure of the clustered grid-connected inverter

图6 谐振分析电路Fig.6 Resonance analysis circuit
由图6可知谐振频率计算公式为:
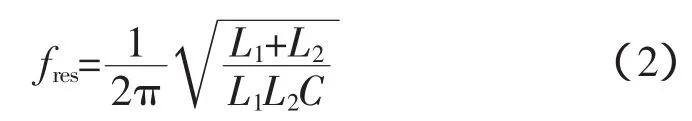
由式(2)可知谐振频率会随着LC的增大而减小。集群并网逆变器控制如图7所示[16]。

图7 集群并网逆变器控制图Fig.7 Control system of the clustered gridconnected inverter
图7中,iref为参考电流;us为电网电压;ip为光伏集群并网系统中其他并联逆变器的电流总和;iL2为逆变器并网电流;kp+ki/s为PI控制器控制参数;kpwm为桥路PWM等效增益。由梅森公式知并网电流iL2对参考电流的传递函数PiL2、对其他并联逆变器电流ip的传递函数PpL2和对电网电压us的传递函数PsL2分别为:
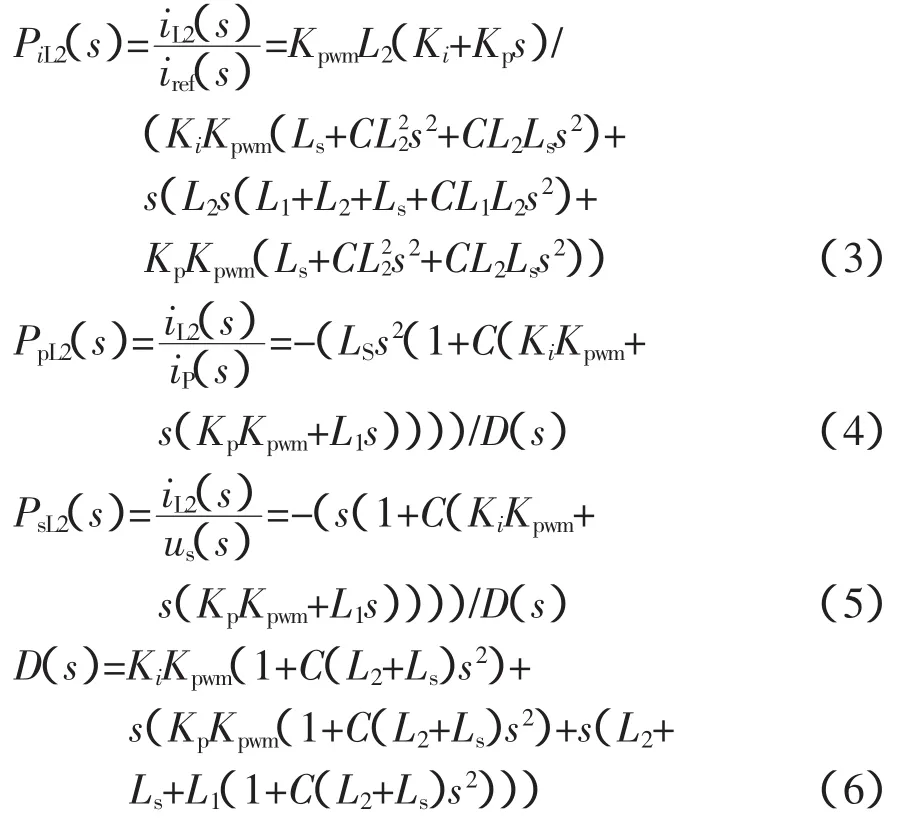
取并联逆变器台数为2,绘制以上传递函数的Bode图分别如图8所示。由图8可知:PiL2、PpL2和PsL2存在2个谐振点,低频谐振频率为467 Hz,高频谐振频率为11 300 Hz。
对比图4和图8可知,与传统光伏并网系统存在单个谐振点相比,光伏集群并网系统谐振点变为2个。分布式光伏集群并网谐振与逆变器自身、其他并联逆变器以及电网存在着复杂的耦合关系。由此可以确定表1系统参数下,分布式光伏集群谐振频率范围为[467 Hz,11 300 Hz]。

图8 集群并网谐振耦合系数Fig.8 Clustered grid-connected resonant coupling coefficient
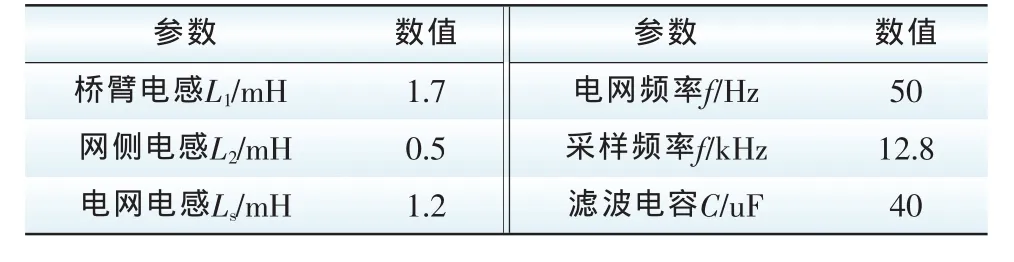
表1 系统参数Tab.1 System parameters
2 LC参数对谐振频率的影响
2.1电网阻抗对谐振的影响
以电网阻抗Ls为例,取并联逆变器台数为3,改变分布式光伏集群并网系统中Ls参数,电网阻抗对谐振的影响(逆变器自身、与其他并联逆变器、与电网谐振耦合系数)如图9所示。
由图9得到电网阻抗对谐振的影响结果如表2所示。可知,随着电网阻抗的增大,低频谐振频率呈减小的趋势,高频谐振频率不变。

表2 电网阻抗对谐振的影响结果Tab.2 Effect result of grid impedance on resonance
2.2滤波电容对谐振的影响
改变滤波电容C的参数,逆变器并联台数取3,滤波电容对谐振的影响如图10所示。由图10得到C对谐振的影响结果如表3所示。

表3 滤波电容对谐振的影响结果Tab.3 Effect result of filter capacitor on resonance
由表3可知,随着滤波电容的增大,不仅低频谐振频率向低频方向移动,而且高频谐振频率也向低频方向移动。总之,电网阻抗和滤波电容的增加会引起谐振频率减小,与之前理论分析结果一致,证明了结论的正确性。

图9 电网阻抗对谐振的影响Fig.9 Influence of grid impedance on resonance
3 并网逆变器台数对谐振频率的影响
通过改变分布式光伏集群并网系统中并联逆变器台数,来研究其对谐振的影响。不同台数下逆变器自身、其他并联逆变器以及电网谐振耦合系数的Bode图如图11所示。
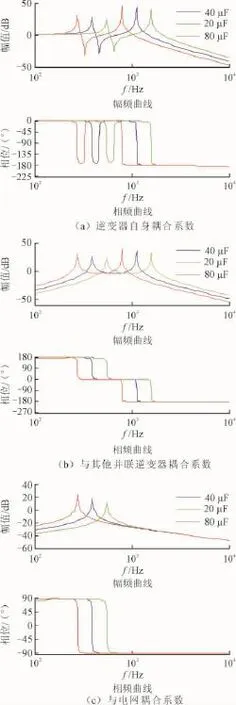
图10 滤波电容对谐振的影响Fig.10 Influence of filter capacitor on resonance
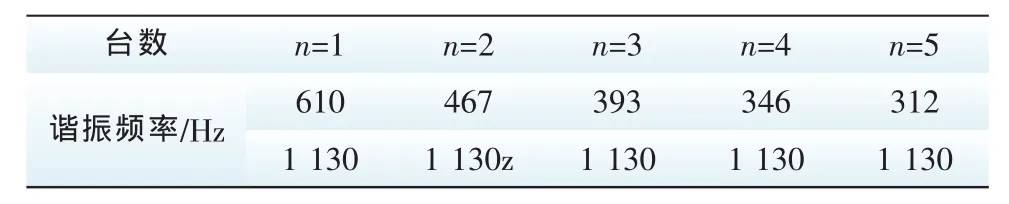
表4 并联逆变器台数对谐振的影响结果Tab.4 Effect result of the number of the grid-connected inverter on resonance
由图11可以得到并联逆变器台数对谐振的影响结果如表4所示。可知,低频谐振峰会随着台数的增加而向低频方向移动,高频谐振峰不会随着台数的变化而变化,与之前的理论分析结果相一致。
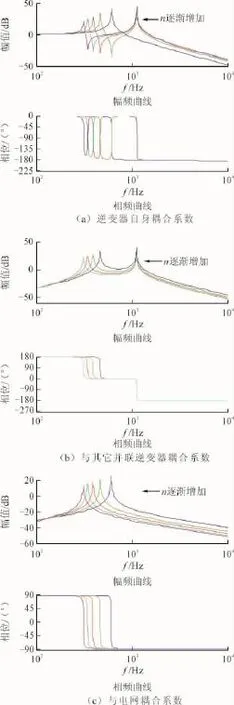
图11 并网逆变器台数对谐振的影响Fig.11 Influence of the number of grid-connected inverters on resonance
4 网架结构变化对谐振频率的影响
4.1网架结构对谐振影响机理
分布式光伏集群入网系统网架结构变化导致各个分布式光伏入网的线路阻抗不再相同,即随着线路阻抗的变化,逆变器之间、逆变器和电网之间的谐振耦合关系也变得更加复杂,谐振分析也更加繁琐。分布式光伏集群并网系统网架结构如图12所示[17]。

图12 分布式光伏集群系统网架结构Fig.12 Grid structure of clustered distributed PV system
由图12可知节点2和节点4后阻抗分别为:

则系统等效阻抗为:

假设系统网架结构发生变化如图13所示。

图13 网架结构变化后的分布式光伏集群系统Fig.13 Clustered distributed PV system after the grid structure change
比较图12和图13可知节点2和节点4之间新增加了一条支路,对网架变化后的结构进行星角变换如图14(a)所示。图14(b)为图14(a)的进一步简化。

图14 分布式光伏集群系统简化电路Fig.14 Simplified circuit of the clustered distributed PV system
其中:L1=Ll1Ll3/LΣ,L2=Ll1Ll5/LΣ,L3=Ll3Ll5/LΣ,LΣ= Ll1+Ll3+Ll5。
进一步将图14(a)简化,等效电路如图14(b)所示。
则网架结构变化后系统等效阻抗为:
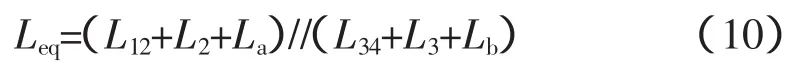
由图14结果代入式(9)得到网架结构变化后系统的等效阻抗为:

其中:
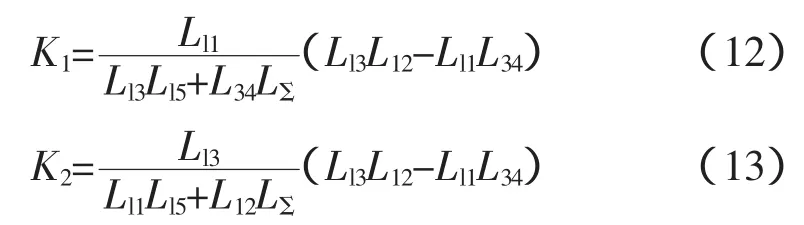
比较式(9)和式(11)可知,在节点2和4之间增加支路导致系统等效阻抗减小,并由(2)的分析结果可知阻抗的减小会引起谐振频率的增大。
4.2仿真验证
根据图12的系统网架结构,在MATLAB/ SIMULINK中搭建光伏集群模型,仿真参数如表5所示,得到并网电流如图15所示。谐振电流的FFT分析结果如图16所示。

表5 仿真参数Tab.5 Simulation parameters

图15 网架结构变化前并网电流谐振信号Fig.15 Grid-connected current resonance signal before grid structure change
由图16可知,网架结构变化前并网电流包含的谐波成分主要是5次和14次谐波。可以知道14次谐波的谐波畸变率为33.71%,明显高于其他次谐波的含量,可以确定谐波频率为700 Hz。

图16 网架结构变化前并网电流谐振信号的FFT分析Fig.16 FFT analysis of grid-connected current resonance signal before grid structure change
根据图13的系统网架结构,在MATLAB/ SIMULINK中搭建光伏集群模型,得到并网电流如图17所示。谐振电流的FFT分析结果如图18所示。
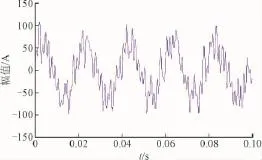
图17 网架结构变化后并网电流谐振信号Fig.17 Grid-connected current resonance signal after grid structure change
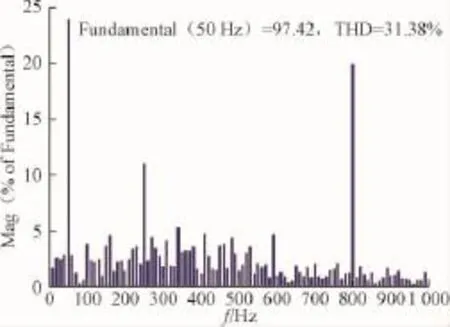
图18 网架结构变化前并网电流谐振信号的FFT分析Fig.18 FFT analysis of grid-connected current resonance signal before grid structure change
由图18可知,网架结构变化后并网电流包含的谐波成分主要是5次和16次谐波。可以知道16次谐波的谐波畸变率为19.93%,明显高于其他次谐波的含量,可以确定谐波频率为800 Hz。
对比图16和图18可知,网架结构变化导致系统等效阻抗减小,进而引起谐振频率的增大,由700 Hz增大到800 Hz。进一步验证了网架结构的变化改变了网络的阻抗参数,进而改变了网络的固有谐振频率,即网架结构变化会对谐振频率和谐振程度产生影响。
5 结论
本文研究了分布式光伏集群并网系统的谐振频率分布范围及其影响因素。本文的工作总结如下:
1)分布式光伏集群并网系统中谐振频率与逆变器自身、其他并联逆变器以及电网存在着耦合关系。谐振频率分布较传统光伏系统更加复杂,谐振频率分布范围在[278 Hz,15 900 Hz]之间。
2)电网阻抗的增大和并联逆变器台数的增加会引起分布式光伏集群低频谐振频率的减小,但高频谐振峰不会发生变化。滤波电容的增大不仅会导致低频谐振频率减小,高频谐振频率也会随之减小。
3)网架结构变化后若是引起分布式光伏集群并网系统等效阻抗减小,则谐振频率会随之增大。
[1]ENSLIN J H R,HESKES P J M.Harmonic interaction between a large number of distributed power inverters and the distribution network[J].IEEE Transactions on Power Electronics,2004,19(6):1586-1593.
[2]AGORRETA J L,BORREGA M,LOPEZ J.Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J].IEEE Transactions on Power Electronics,2011,26(3-4):770-785.
[3]张兴,余畅舟,刘芳,等.光伏并网多逆变器并联建模及谐振分析[J].中国电机工程学报,2014,34(3):336-345.ZHANG Xing,YU Changzhou,LIU Fang,et al.Modeling and resonance analysis of multi-paralleled grid-tied inverters in PV systems[J].Proceedings of the CSEE,2014,34(3):336-345(in Chinese).
[4]陆晓楠,孙凯,黄立培.微电网系统中并联LCL滤波器谐振特性[J].清华大学学报(自然科学版),2012,52(11):1571-1577.LU Xiaonan,SUN Kai,HUANG Lipei.Resonance characteristics in a parallel LCL filter system of microgrid applications[J].Journal of Tsinghua University(Natural Science Edition),2012,52(11):1571-1577(in Chinese).
[5]丁明,王伟胜,王秀丽,等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报,2014,34(1):1-14.DING Ming,WANG Weisheng,WANG Xiuli,et al.A review on the effect of large-scale PV generation on power systems[J].Proceedings of the CSEE,2014,34(1):1-14(in Chinese).
[6]周林,张密,居秀丽,等.电网阻抗对大型并网光伏系统稳定性影响分析[J].中国电机工程学报,2013,33(34):34-41.ZHOU Lin,ZHANG Mi,JU Xiuli,et al.Stability analysis of large-scale photovoltaic plants due to grid impedances[J].Proceedings of the CSEE,2013,33(34):34-41(in Chinese).
[7]曾正,赵荣祥,吕志鹏,等.光伏并网逆变器的阻抗重塑与谐波谐振抑制[J].中国电机工程学报,2014,34(27):4547-4558.ZENG Zheng,ZHAO Rongxiang,LÜ Zhipeng,et al.Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems[J].Proceedings of the CSEE,2014,34(27):4547-4558(in Chinese).
[8]郑志杰,李磊,王葵.大规模光伏并网电站接入系统若干问题的探讨[J].电网与清洁能源,2010,26(2):74-76.ZHENG Zhijie,LI Lei,WANG Kui.Discussions on some issues of large scale PV grid connected system[J].Power System and Clean Energy,2010,26(2):74-76(in Chinese).
[9]刘怀远,徐殿国,武健,等.并网换流器系统谐振的分析、检测与消除[J].中国电机工程学报,2016,36(4):1061-1074.LIU Huaiyuan,XU Dianguo,WU Jian,et al.Analysis,detection and mitigation of resonance in grid-connected converter systems[J].Proceedings of the CSEE,2016,36(4):1061-1074(in Chinese).
[10]王亮,王志新,陆斌锋,等.基于LCL滤波器的单相光伏并网逆变控制器设计[J].电网与清洁能源,2014,30(12):114-118.WANG Liang,WANG Zhixin,LU Binfeng,et al.Design of the controller of the single phase PV grid-connected inverter with LCL filter[J].Power System and Clean Energy,2014,30(12):114-118(in Chinese).
[11]张国荣,李宗钧,陈鹏.并联有源电力滤波器中LCL滤波器的分析与设计[J].高压电器,2011,47(6):19-22.ZHANG Guorong,LI Zongjun,CHEN Peng.Analysis and design of LCL-filter in shunt active power filter[J].High Voltage Apparatus,2011,47(6):19-22(in Chinese).
[12]LAVOPA E,ZANCHETTA P,SUMNER M,et al.Realtime estimation of fundamental frequency and harmonicsfor active shunt power filters in aircraft electrical systems[J].IEEE Transactions on Industrial Electronics,2009,56(8):2875-2884.
[13]WANG X,PANG Y,LOH P C,et al.A series-LC-filtered active damper with grid disturbance rejection for ac power electronics based power systems[J].IEEE Transactions on Power Electronics,2015,30(8):4037-4041.
[14]RODRIGUEZ P,LUNA A,CANDELA I,et al.Multiresonant frequency-lockedloopforgridsynchronization of power converters under distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2011,58(1):127-138.
[15]孙振奥,杨子龙,王一波,等.光伏逆变器集群的谐振原因及其抑制方法[J].中国电机工程学报,2015,35(2):418-425.SUN Zhen'ao,YANG Zilong,WANG Yibo,et al.The cause analysis and suppression method of resonances in clustered grid-connected photovoltaic inverters[J].Proceedings of the CSEE,2015,35(2):418-425(in Chinese).
[16]周林,张密,居秀丽,等.电网阻抗对大型并网光伏系统稳定性影响分析[J].中国电机工程学报,2013,34(34):34-41.ZHOU Lin,ZHANG Mi,JU Xiuli,et al.Stability analysis of large-scale photovoltaic plants due to grid impedances[J].Proceedings of the CSEE,2013,34(34):34-41(in Chinese).
[17]胡伟,孙建军,马谦,等.多逆变器并网系统谐振特性分析[J].电力自动化设备,2014,34(7):93-98.HU Wei,SUN Jianjun,MA Qian,et al.Resonant characteristicsofmulti-invertergrid-connectionsystem[J].Electric Power Automation Equipment,2014,34(7):93-98(in Chinese).
(编辑冯露)
Analysis of Resonance Distribution Range and Influence Factors of Clustered Distributed Photovoltaic
GAO Jing1,LI Peng1,SUN Jian2
(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources(North China Electric Power University),Baoding 071003,Hebei,China;2.State Grid Beijing Electric Power Research Institute,Beijing 100075,China)
In clustered distributed photovoltaic(PV)system,an increase of the PV units turns the system into a high order LC network and the resonant frequency distribution becomes more complex.According to the structure of the clustered distributed PV system,this paper analyzes the resonance of the second order LC network and higher order LC network,and obtains the complex resonant coupling relationship between the inverter itself,the other parallel inverters and the grid,and determines the distribution range of resonant frequency of the clustered distributed grid-connected PV.Based on the resonant coupling relationship,the effects of the grid impedance and filter capacitor parameters,the number of parallel inverters and structure change of the network on the resonant frequency are studied respectively.The simulation results show that the above factors cause changes in the resonant frequency of the clustered distributed PV.
distributed photovoltaic;clustered grid-connected;resonant frequency distribution range;resonant influencing factors
1674-3814(2016)07-0125-07
TM732
A
国家自然科学基金项目(51577068);国家电网公司总部科技项目(520201150012)。
Project Supported by National Natural Science Foundation of China(51577068);Science and Technology Project of State Grid Corporation of China(520201150012).
2016-04-20。
高静(1990—),女,硕士研究生,研究方向为电能质量分析与控制;
李鹏(1965—),男,博士,教授,主要从事新能源并网发电与微电网技术、电能质量分析与控制,柔性输配电技术、电力电子技术在智能电网中的应用等方面的工作。
