多孔质气静压轴承-转子系统的模态分析

侯晓帅， 赵则祥， 张国庆， 王文博， 程旭鹏, 姚　博， 许华威

(中原工学院， 郑州 450007 )



多孔质气静压轴承-转子系统的模态分析

侯晓帅， 赵则祥， 张国庆， 王文博， 程旭鹏, 姚博， 许华威

(中原工学院， 郑州 450007 )

对转子的模态进行分析，基于有限元理论建立了多孔质气静压轴承-转子系统的动力学模型。运用Matlab软件仿真，得到了考虑陀螺与阻尼以及不考虑陀螺与阻尼两种情况的模态振型。在实验验证时，借助Data Physics 730动态信号分析仪进行数据采集，将采集的数据导入用ME’scopeVES软件建立的转子三维模型中进行分析。仿真和实验对比得出，弹性支撑下后置T型转子仿真分析与实验验证的数值相差在6%以内。

转子；模态分析；有限元；阻尼

多孔质气静压轴承-转子系统因具有较高的刚度和较好的动态稳定性等优点而广泛应用于超精密加工行业。但其受设计、计算、加工精度等因素的影响，在外界激励作用下易失稳。当其转速接近或者等于系统的固有频率时，会产生共振，导致转子与轴承接触，甚至发生抱轴事故[1-2]。随着机械设计技术的发展，模态分析在设计过程中扮演着越来越重要的角色。模态分析能够有效地抑制机械振动对设备使用性能和寿命的不良影响。设计人员在设计过程中应尽量避免其固有频率与工作转速相同或接近，对轴承-转子系统的振动采取主动控制，从根本上改变设计方法，以便有效地避免其发生振动。

有限元法基于变分原理，早在1970年便是求解数学物理方程的一种数值方法，用于分析转子动力学[3]。它能同时兼顾所建立模型的完整性和计算效率。它的应用范围已经从静力平衡问题扩展到动力学问题，分析的对象已经从固体扩展到流体[4]。对于多孔质气静压轴承-转子系统而言，结合有限元法，经过数据处理得到动力学方程，基于稳定性理论，可合理化设计气静压轴承-转子系统，在保证不产生共振和“漂移”的前提下对系统进行振动特性分析和控制，使其平稳运转。

为了设备可靠运行，本文基于有限元理论，建立了多孔质气静压轴承-转子动力学模型，研究了多孔质气静压轴承-转子系统的模态，并与实验数据作对比，对提高系统稳定性以及探索其减振措施具有现实的工程意义。

1　有限元理论分析

1.1建立模型

对实验室购进的后置T型转子测量可知，其总长为436 mm，质量为22.298 kg，圆盘和转子直径分别为138 mm和88 mm。在Matlab中输入后置T型转子各个轴段的40Cr材料特性以及单元尺寸参数：弹性模量为206 GPa，泊松比为0.3，密度为7 850 kg/m3。沿轴线方向，把转子质量及转动惯量集中到某个节点上，划分若干单元，使相邻单元在节点处联结。节点选在轴径中心，按顺序从右向左依次编号。进行有限元分析时，将节点位移看作基本未知量，即有限单元在任意瞬时位置都用其单元所含节点的位移来描述，系统内节点位移就构成了广义坐标[5]。在此模型中，将后置T型转子分为 9个单元，共计10个节点。轴段的集中质量和惯量分别为2.583 kg和0.006 2 kg·m2，节点编号为7。该后置T型转子，采用相同刚度和阻尼的多孔质气静压轴承支撑，长度均为100 mm。把两个多孔质气静压轴承的中间位置简化为两个弹性支撑点，节点编号分别为2和5，中心跨距为160 mm。两个支撑位置分别在距离右端面 0.06 m和0.22 m处(见图1)。

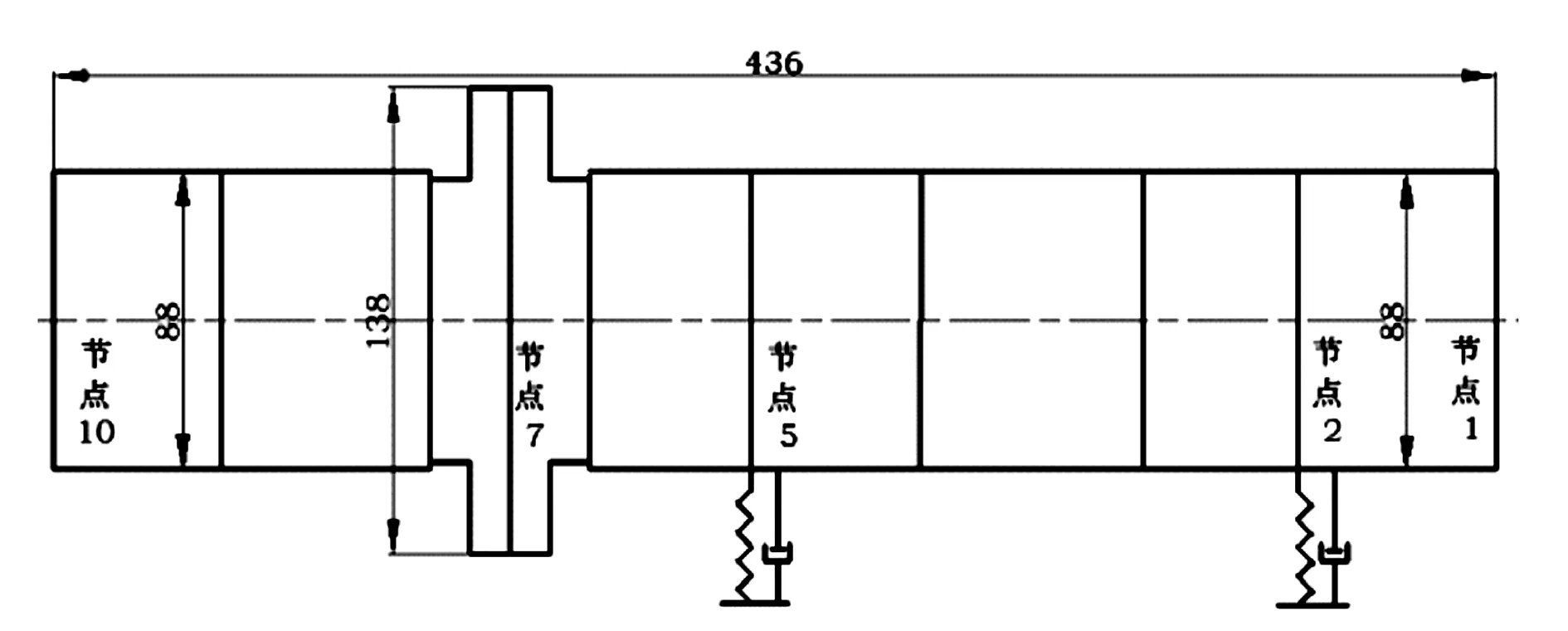
注：图中尺寸单位均为mm。图1　后置T型转子模型

1.2Timoshenko梁理论

针对该转子模型，采用剪切变形的Timoshenko梁有限元理论，建立转子各个轴单元的单元刚度、单元质量和单元惯量等矩阵[6]。对各单元进行分析，建立各单元节点的力与位移之间关系，综合各单元的运动方程，可整理出以节点位移为广义坐标的系统运动微分方程。对于整个系统而言，一个质量连续分布的转子振动问题就转化成了有限自由度的振动问题[7]。将刚性圆盘的质量和惯量加入转轴的刚度、质量和惯量等矩阵，依据有限元原理，可将这三类单元阵组合成转子系统的刚度、质量和阻尼等矩阵。

2　阻尼和刚度求解

为了更好地对系统进行动态性能分析，需要建立系统的动力学方程。对轴承的动力学特性分析时，需要计算轴承的刚度和阻尼，其对转子的临界转速和稳定性起着关键性的作用[8]。刚度影响着由不平衡力或外加振动所引起的谐振的频率。轴承是产生阻尼的源头，它限制着振动或谐振点的涡动幅度。当阻尼为0时，产生自激不稳定。在转子作微小涡动的情况下，轴承支撑可当作线性化弹簧与阻尼来处理，运用Fluent软件对多孔质气静压轴承的流场进行仿真，得到径向和轴向的气膜力，从而求出系统的阻尼和刚度。

2.1阻尼的计算

当转速为10 000 r/min时，计算偏心量(e1)为1 μm和涡动速度(Ω1)为0的情况下，由于气膜间隙不均匀而产生的径向气膜力的值Fr0和轴向气膜力的值Ft0。在偏心量不变的情况下，给定一个涡动速度扰动ΔΩ=5 000 r/min,得到此时径向气膜力的值Fr1和轴向气膜力的值Ft1。主阻尼C和交叉阻尼c可按式(1)求解[9]。

(1)

2.2刚度的计算

保持转速10 000 r/min不变，外加一个微小的偏心扰动量Δe=1 μm，重新建模。在保持涡动速度Ω1为0的情况下，得到此时径向气膜力的值Fr2和轴向气膜力的值Ft2。主刚度K和交叉刚度k可按式(2)求解。

(2)

轴承的刚度(Kxx、Kyy—主刚度，kxy、kyx—交叉刚度)和阻尼(Cxx、Cyy—主阻尼，cxy、cyx—交叉阻尼)等都是在静平衡位置轴承作小扰动的假设下，用数值方法计算得到的。由于所建立模型的x、y轴均具有对称性，因此，主刚度Kxx=Kyy=K，交叉刚度kxy=-kyx=k，主阻尼Cxx=Cyy=C，交叉阻尼cyx=-cxy=c。将已设定条件代入式(1)和式(2)，得到多孔质气静压轴承刚度和阻尼，如表1所示。

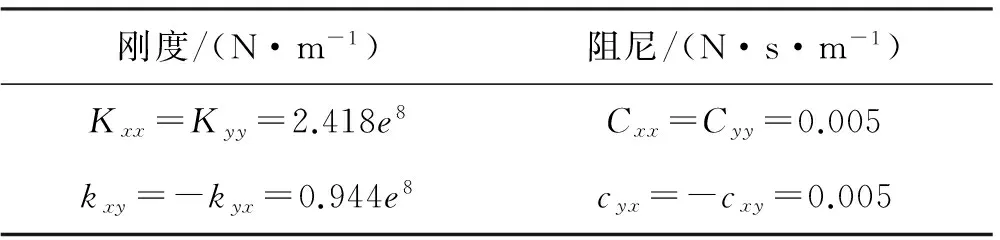
表1　多孔质气静压轴承的刚度及阻尼

3　Matlab仿真模态阵型

将上述计算得到的轴承刚度和阻尼加入系统的刚度、质量和阻尼等矩阵，可建立轴承-转子系统的运动方程[10]：

(3)

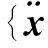
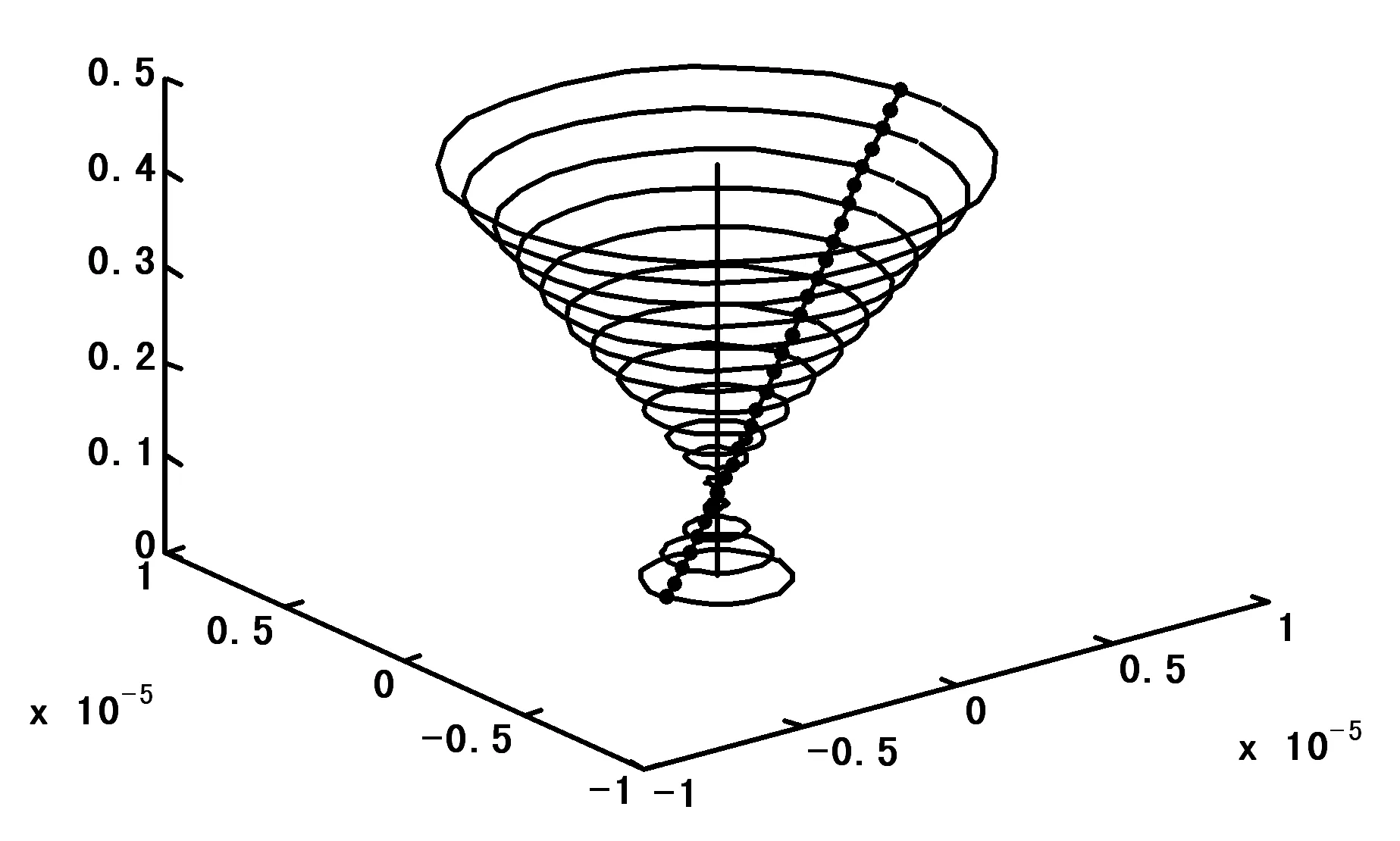
(a)一阶模态振型

(b)二阶模态振型注：图中尺寸单位均为m。图2　考虑陀螺与阻尼的模态振型

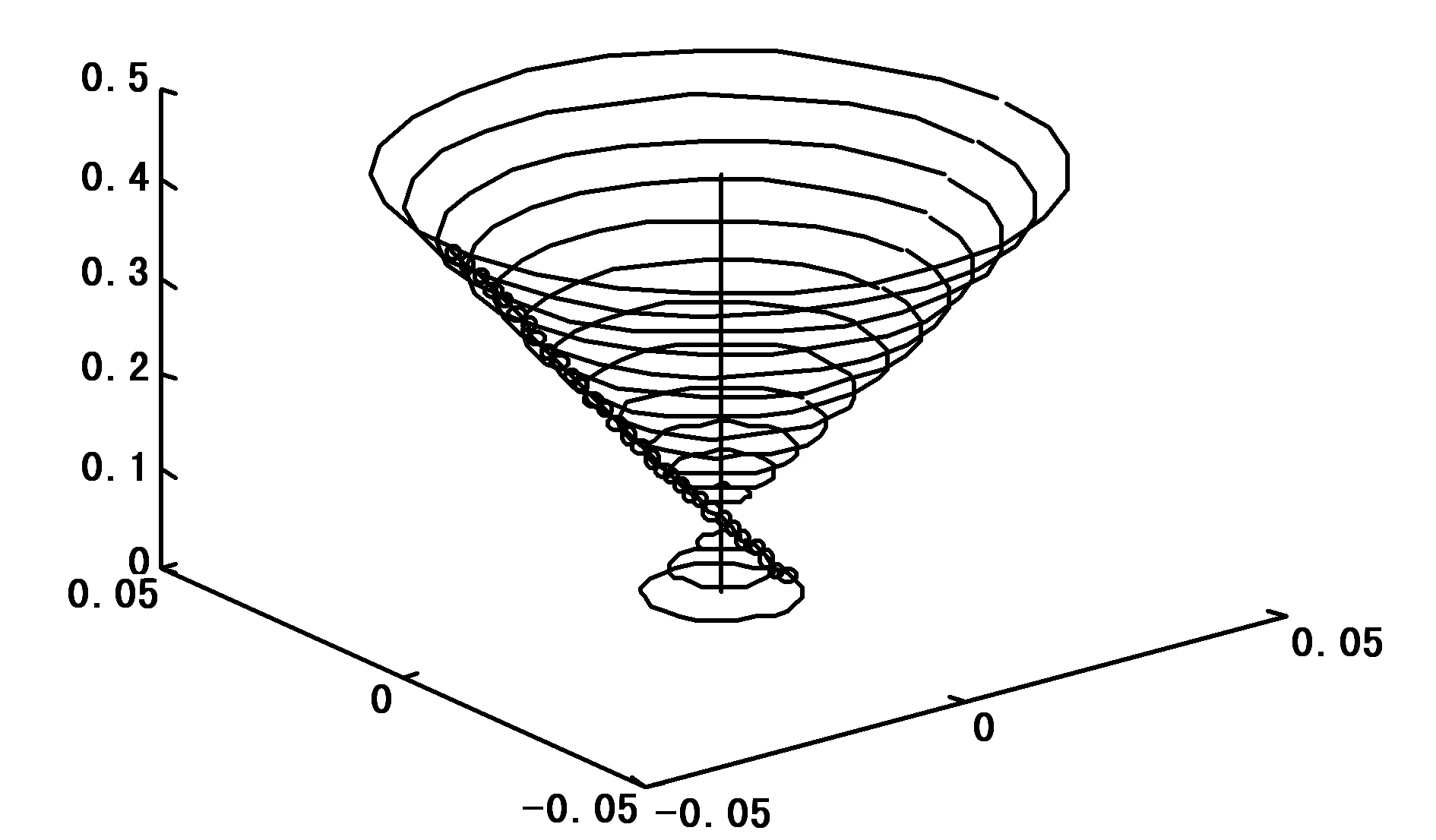
(a)一阶模态振型

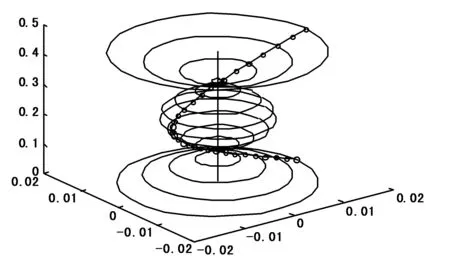
(b)二阶模态振型

(c)三阶模态振型注：图中尺寸单位均为m。图3　不考虑陀螺与阻尼的模态振型

4　实验分析

4.1实验验证

实验时将转子用弹性物体(塑料)支撑。模态实验器材如图4所示。在实验验证中，该后置T型转子每个节点有4个响应点。借助ME’scopeVES软件建立的后置T型转子三维模型如图5所示。

图4　实验器材

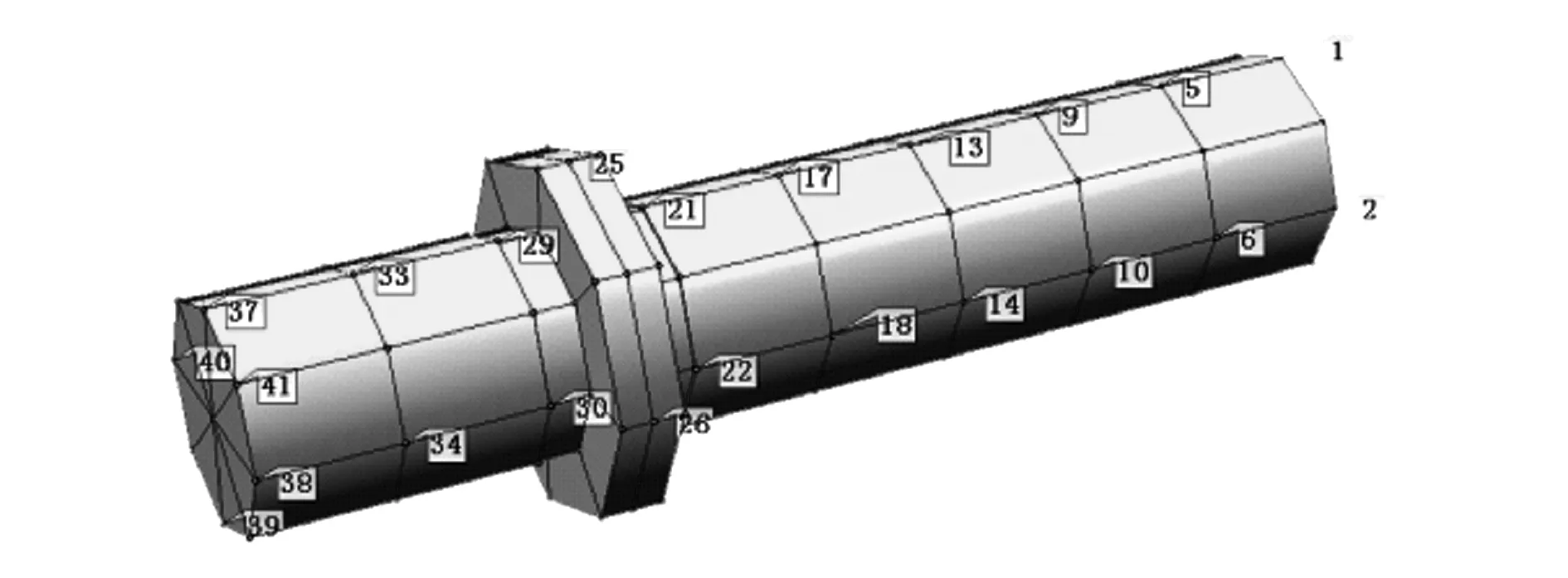
图5　后置T型转子三维模型

借助Data Physics 730动态信号分析仪对后置T型转子进行数据采集。在传递函数模块下，带宽设置为10 kHz，加窗方式设置为F/Exp，触发方式设置为input，触发力设置为50 N。力锤敲击点位置在三维模

型的第41点处；响应点为1～40，共40个点。数据的采集使用ICP 加速度传感器，实验使用的两个传感器(每个传感器有x、y、z3个方向)共6个通道(通道2～7)，使它们两两按逆时针90°相互垂直放置。力锤和传感器对应通道显示器如图6所示。图6中通道1为力锤的敲击信号，范围为10 V。通道2和道通5对应传感器x方向信号，通道4和通道7对应传感器z方向信号，范围均为5 V。由于沿转子轴向无信号输出，因此，y方向对应的通道3和通道6无响应。在实验中，手动移动加速度传感器到相应响应点时，力锤敲击某个响应点，采集数据信号。其输出如图7所示。

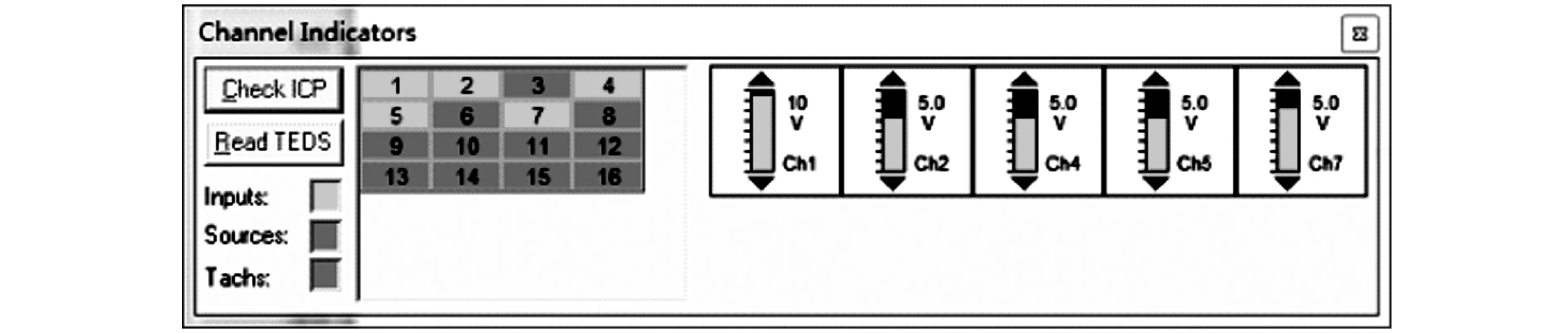
图6　力锤和传感器对应通道显示器

(a)力锤的敲击信号

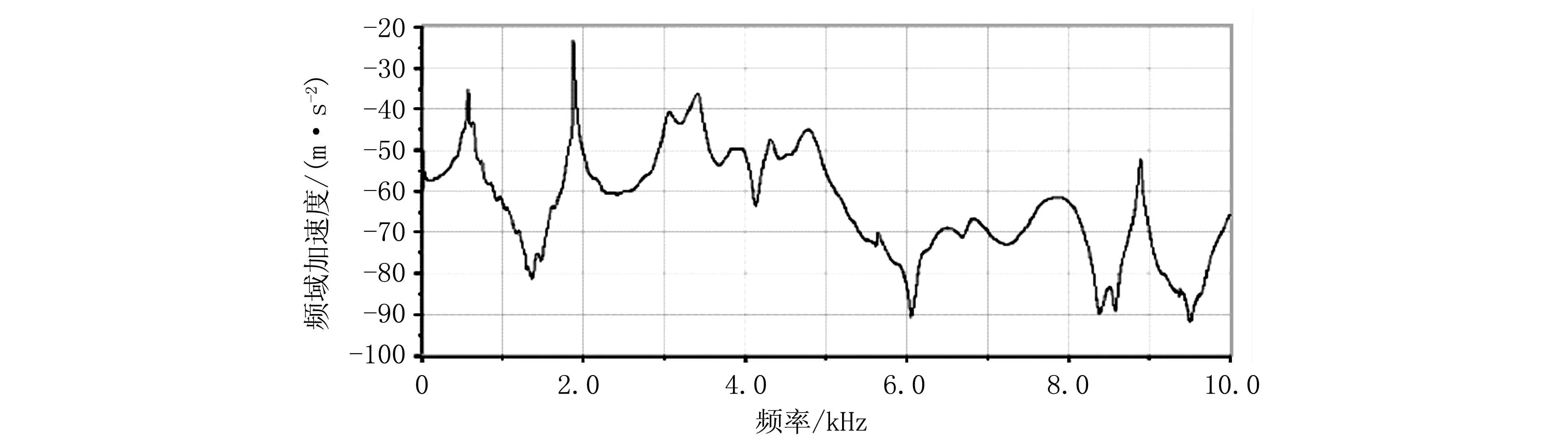
(b)某个响应点的响应信号图7　力锤和某个响应点的信号输出

将本次实验采集到的40个响应点，共计80个响应信号的数据，导入运用ME’scopeVES软件建立的后置T型转子三维模型中，通过设置模态参数，进行数据拟合处理并输出分析结果，可得到后置T型转子的模态数值。后置T型转子的实验与仿真结果对比如表2所示。

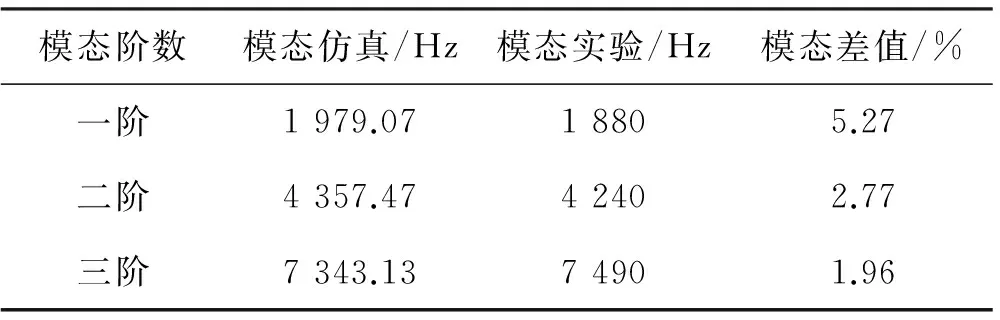
表2　仿真与实验结果对比

从表2可知，第三阶模态实验值与仿真分析值相差最大，约147 Hz，但各阶模态实验值与仿真分析值相差都在6%以内。

4.2原因分析

(1)实验中所用弹性支撑物的实际宽度较大，当用传感器测量弹性支撑的节点时，弹性支撑物的位置有所变化，而理论研究时，只是把弹性支撑物的位置看作单个节点，作为支撑点来对待。

(2)用力锤进行敲击实验时，由于人为原因，作用力大小和作用点位置有较小变动。

5　结　语

对多孔质气静压轴承-转子系统的模态分析，得出了以下结论：在弹性支撑下，后置T型转子仿真分析与实验验证的数值相差在6%以内。证明了基于有限元理论的数值计算方法的正确性。本研究为多孔质气静压轴承-转子系统模态分析及其设计提供了参考。

[1]Lin J R. Optional Design of One Dimensional Porous Slider Bearings Using Brinkman Model[J]. Tribology International, 2001，34(1)：65-73.

[2]Stout K J, Barraus S M. The Design of Aerostatic Bearing for Application to Nanometer Resolution Manufacturing Machine Systems[J]. Tribology International, 2000，33(12)：803-809.

[3]Duhl R L. Dynamics of Distributed Parameter Turbo Rotor Systems Transfer Matrix and Finite Element Techniques[D]. Ithaca:Cornell University, 1970.

[4]赵经文. 有限元方法[M]. 哈尔滨：哈尔滨工业大学出版社，1998.

[5]章正传. 小孔节流静压气浮轴承-转子系统动力学特性研究[D]. 哈尔滨：哈尔滨工业大学，2006.

[6]Lee S Y, Lin S M,Lin Y S. Instability and Vibration of A Rotating Timoshenko Beam with Precone[J]. International Journal of Mechanical Sciences, 2009，51(2)：114-121.

[7]李祖辉，童水光，郭涛. 大型透平膨胀机转子动力学分析[J]. 化工机械，2006，33(1)：21-23.

[8]钟一谔，何衍宗，王正，等. 转子动力学[M]. 北京：清华大学出版社，1987.

[9]于贺春. 高速静压气体轴承-转子系统的特性研究[D]. 大连：大连海事大学，2011.

[10]刘延柱，陈文良. 振动力学[M]. 北京：高等教育出版社，2006.

(责任编辑：王长通)

Model Analysis of Porous Aerostatic Bearing-rotor System

HOU Xiao-shuai, ZHAO Ze-xiang, ZHANG Guo-qing, WANG Wen-bo,CHENG Xu-peng, YAO Bo, XU Hua-wei

( Zhongyuan University of Technology, Zhengzhou 450007，China )

For the modal analysis of a rotor, a dynamic model of porous aerostatic bearing-rotor system is established based on the theory of finite element. The modal vibration models, in which the gyroscopic and damping influence is considered and is not considered, are gained respectively through simulation analysis by using Matlab software. The data collected by Data Physics 730 dynamic signal analysis instrument are put in the three-dimensional model of the rotor established by ME’scopeVES to analyze in experimental verification. According to the results of simulation compared with experiment, numerical value of theoretical analysis and experimental verification are similar within 6% under elastic support with the rear rotor of T type.

rotor；modal analysis；finite element；damping

2016-06-10

国家自然科学基金项目(51475485)

侯晓帅(1990-)，男，河南漯河人，硕士生，主要研究方向为精密制造技术与装备。

1671-6906(2016)04-0023-05

TH113.1

A

10.3969/j.issn.1671-6906.2016.04.005