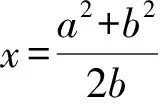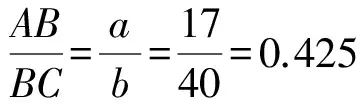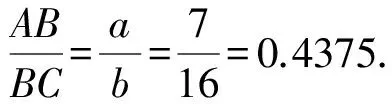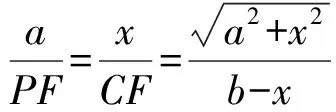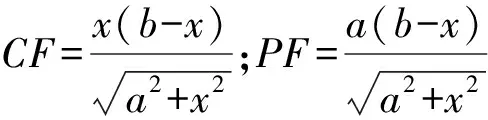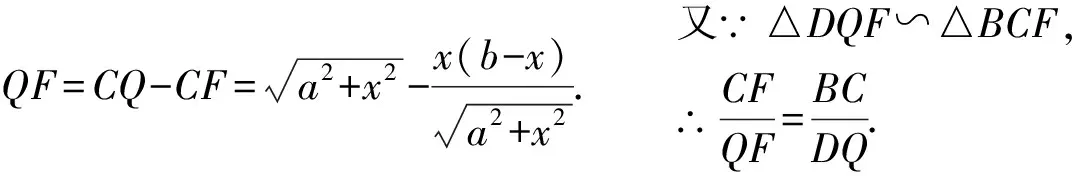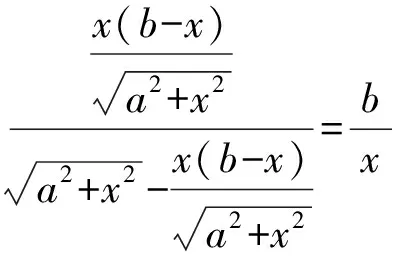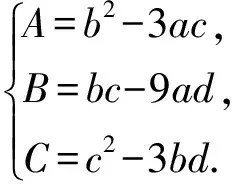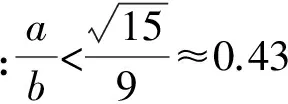一道平面几何题的探究历程

安徽省合肥市第一中学

李涵秋　　(邮编：230601)



一道平面几何题的探究历程

安徽省合肥市第一中学

李涵秋(邮编：230601)

学习是一个不断探索的过程.学习数学的最主要的目的是培养数学思维能力.在高中数学学习过程中，不仅要理解数学学习的本质因素与数学学习的过程，还应当在数学学习过程中，培养属于自己的数学思维方法，比如抽象性的数学思维方法、建构性的数学思维方法等.更重要的是要锻炼自己发现问题、提出问题、分析问题以及解决问题的思维品质.笔者以下面一道平面几何题的探究过程为例，谈谈数学学习过程中的问题探究，供大家借鉴与思考.

1　问题呈现

1.1原题

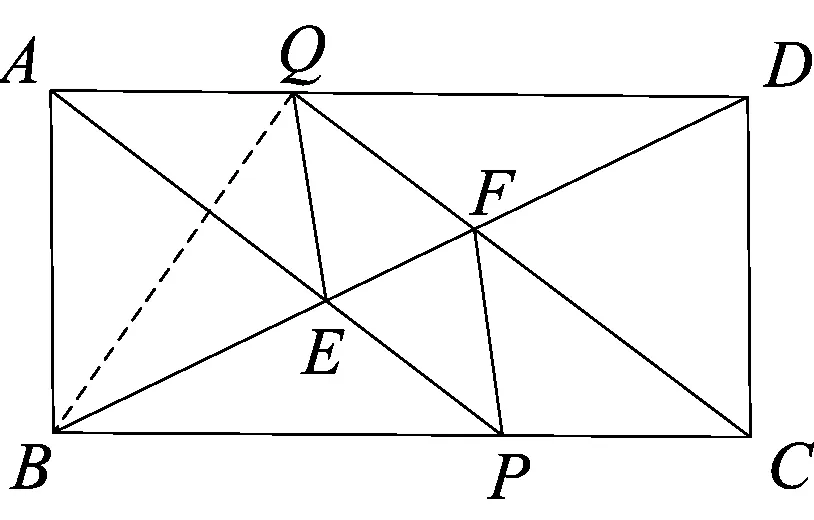
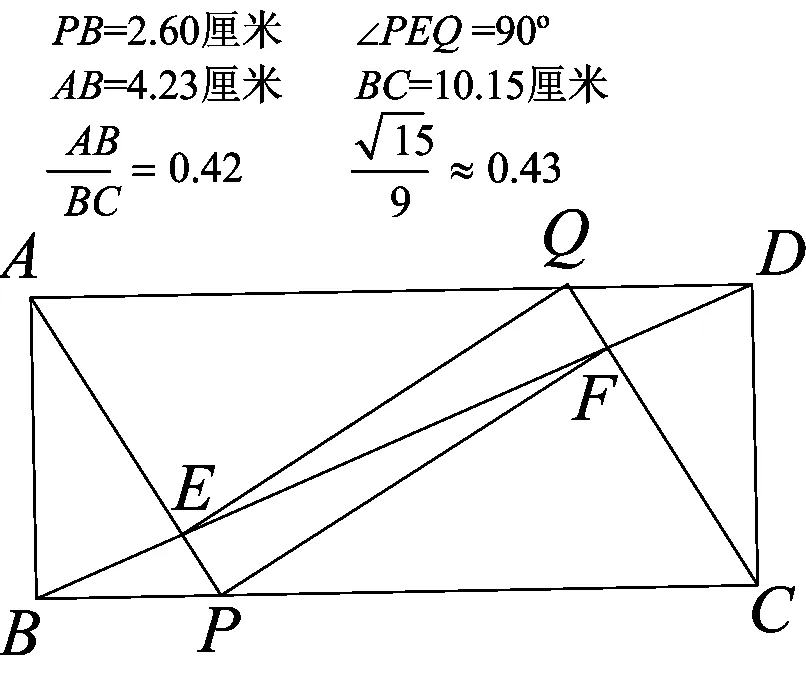
如图1，矩形ABCD中，P、Q分别在边BC和AD上，且BP=DQ，连接AP、CQ分别交对角线BD于E、F，连接EQ、FP，判断四边形EPFQ的形状，并证明.

图1

解 四边形EPFQ的形状是平行四边形，理由如下：

证明∵BP=DQ，四边形ABCD为矩形，

∴AQ=CP且AQ∥CP.

∴ 四边形APCQ为平行四边形，

∴AP∥CQ，

易证△DFQ≌△BEP，

∴FQ=EP，

∴FQPE，

故四边形EPFQ为平行四边形.

1.2问题发现

(1)知识点分析：本题主要运用了矩形的性质、平行四边形的判定以及三角形全等的知识.解决此题的方法有很多，上面只是提供了一种证明思路.

(2)拓展区分析：本题值得思考的地方有很多，比如原题中证明的平行四边形会不会是特殊的平行四边形，如菱形、矩形、正方形等？如果是特殊的平行四边形，原题中提供条件显然不够，那么成立的条件是什么？这个问题值得探究与思考.

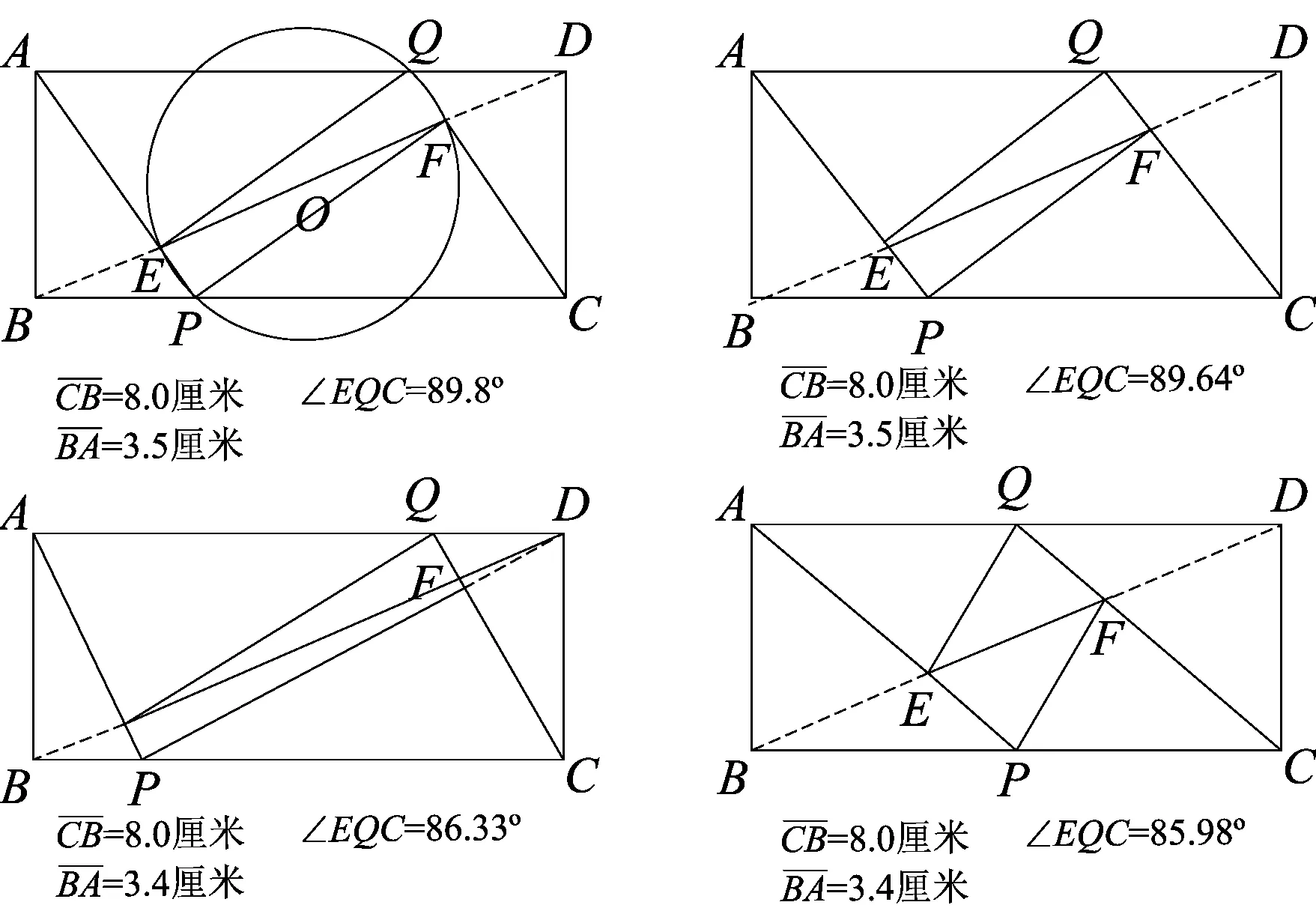
2　拓展探究

2.1探究一

(1)问题提出

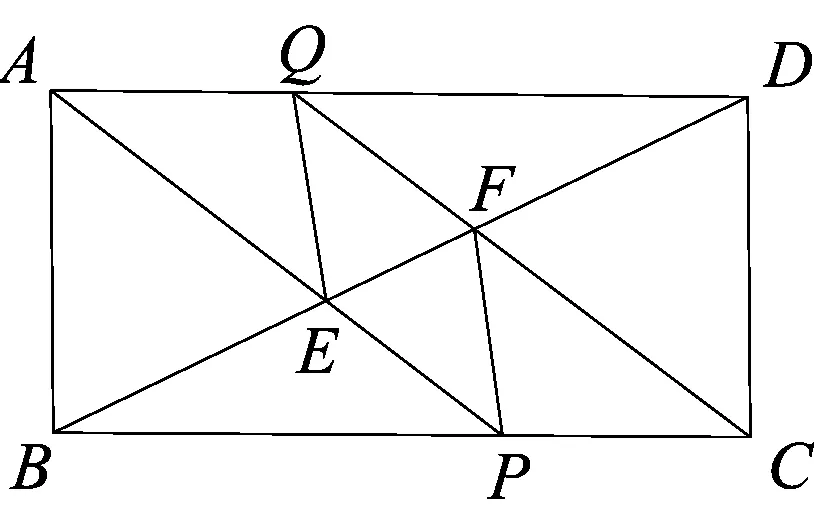
图2

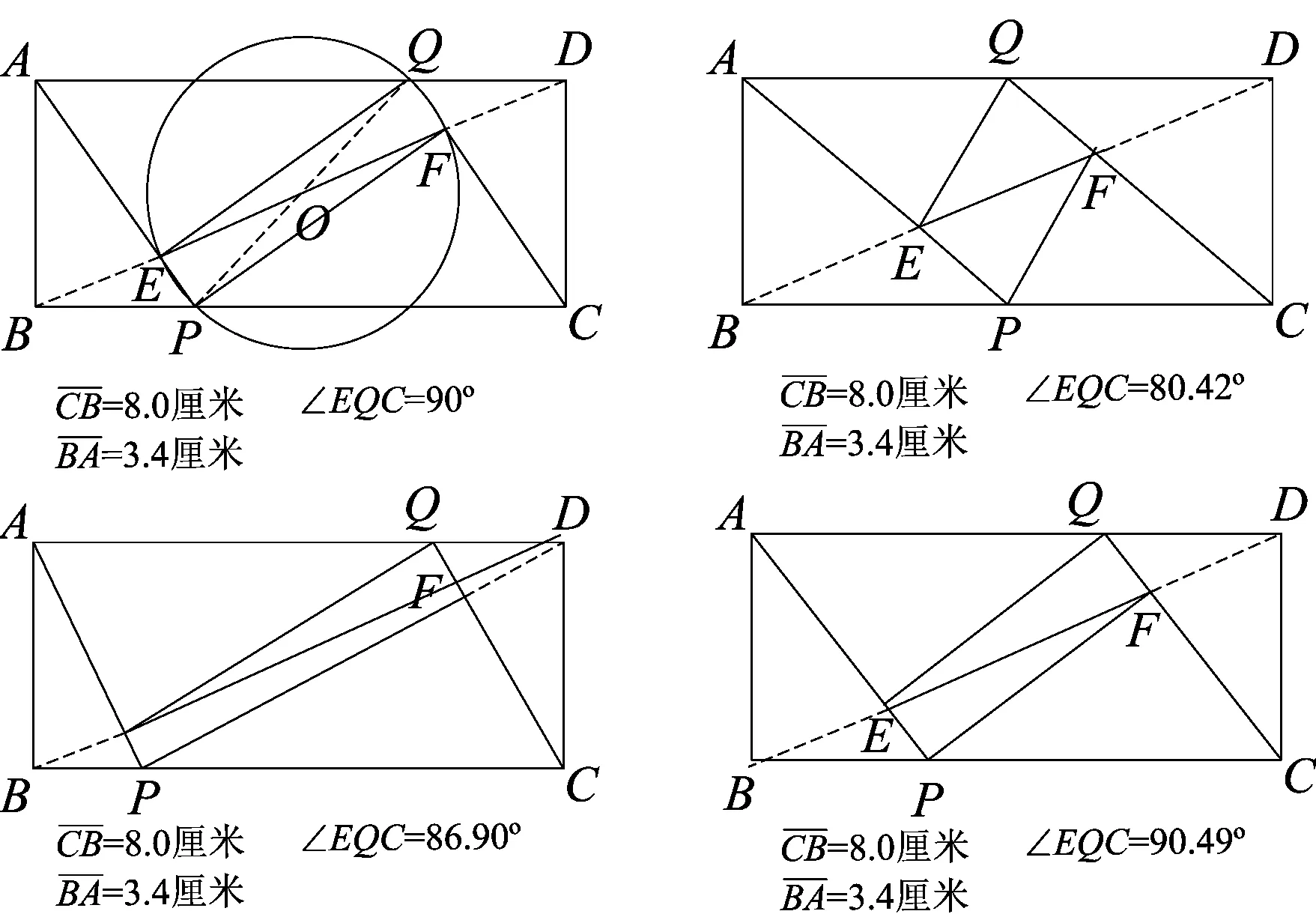
如图2，矩形ABCD中，设AB=a，BC=b(a

(2)问题分析

菱形是对称图形.由于线段AB小于线段AD，也就保证了菱形存在的必然性.在原题已经证明的平行四边形的基础上，若平行四边形QEPF是菱形，则线段PQ与线段EF一定垂直平分，此时，EQ=EP，∠FEQ=∠FEP.所以，线段BP和线段BQ的长度一定相等.连接线段BQ，即可以运用勾股定理找到x与a、b之间的关系.

(3)问题解决

图3

解析如图3，若四边形PEQF是菱形，可知点P和点Q关于直线BD对称，所以BQ=BP=x，

2.2探究二

(1)问题提出

图4

如图4，矩形ABCD中，AB=a，BC=b(a

(2)问题分析

借助几何画板软件验证是否存在：

图5

图6

(3)问题解决

根据上面几何画板软件测量工具，发现四边形EPFQ是否会是矩形，与矩形ABCD中AB和CD的长度有关，也就是说与宽长之比有关.那么宽长之比满足什么条件时，四边形EPFQ可以是矩形？

①如图4，若四边形EPFQ是矩形，

则∠ABP=∠EPF=∠QFP=90°.

易证△ABP∽△PFC,

化简得：x3+bx2-b2x+a2b=0.

也就是说，当a,b满足什么条件时，这个一元三次方程有解？有解则矩形存在，若无解，则矩形不存在.

由盛金公式：

一元三次方程ax3+bx2+cx+d=0,(a,b,c,d∈R且a≠0)

总判别式△=B2-4AC.

由△=B2-4AC

=(-b3-9a2b)2-4×4b2(b4-3a2b2)

=81a4+66a2b2-15b4

=3(27a2-5b2)(a2+b2).

图7

由盛金定理得：

只有当△=B2-4AC=3(27a2-5b2)(a2+b2)<0成立，并有三个实数解.

②借助几何画板可以验证得出该结论的正确性，如图(7)(8)(9)所示：

图8

图9

原题是初中平面几何中的一道几何证明题，难度不大，考查基本的四边形、平行四边形、矩形以及三角形全等等知识.学习的最终目的是运用已有知识去发现探究更多的未知领域.这就需要我们能发现问题并主动提出问题，进而分析问题并解决问题.

1邵泉成.高中生数学学习与数学思维方法探究[J].成才之路, 2015(13):72-73

2王永. 论中学生数学思维方法的培养[J].魅力中国, 2010(32):178-178

2016-06-26)