对一次函数图象教学难点突破的尝试与思考

浙江省衢州市柯城区石梁中学

余利英　　(邮编：324015)

上海市岭南中学

刘华为　　(邮编：200435)



聚焦新课程

对一次函数图象教学难点突破的尝试与思考

浙江省衢州市柯城区石梁中学

余利英(邮编：324015)

上海市岭南中学

刘华为(邮编：200435)

从一个实例入手，以作图为主线，以几何画板动态演示为辅助，从直观感受到动手操作、从具体到抽象、从有限到无限、从大胆猜想到合情推理，引导学生逐步认识、理解一次函数的图象是一条直线，从而巧妙地突破一次函数图象的教学难点．

一次函数图象；数学理解；难点突破

1　难点分析

众所周知，一次函数y=kx+b(k≠0)的图象是一条直线，主要包含两方面含义：其一，以满足关系式y=kx+b的任一组x、y的值分别为横纵坐标的点都在这条直线上(完备性)；其二，直线上所有点的横纵坐标x、y的值皆满足关系式y=kx+b(纯粹性)．显然，单纯从这两个方面去阐述一次函数y=kx+b的图象就是一条直线，对于初次接触作函数图象(之前学生只是知道图象法也是函数的三种表示方法之一和函数图象的概念)的初中学生来说，在理解和接受上存在一定的难度．因此，浙教版教材(八·下)对一次函数图象的处理主要基于感知上(回避了难点)，通过“列表、描点和连线”三步操作，引导学生观察出一次函数图象是一条直线，至于为什么坐标满足关系式y=kx+b的点组成的图形就是一条直线却未作任何理解性设计．但“列表、描点、连线”得出一条直线后就硬说是一次函数的图象，有“强塞”之感．学生不仅感到突兀，而且不易接受与理解，当然用起来也就难免将信将疑，对后续学习造成了一定的干扰．即使经过反复强化，学生从感观上接受了一次函数的图象是一条直线，但在理解上仍然存在一定的障碍．

那么，如何设计课堂教学方能引导学生理解性地认知一次函数y=kx+b的图象就是一条直线呢？首先，需从直线的动态生成入手，找到理解一次函数图象是一条直线的切入点．众所周知：点动成线．但点动未必成直线，只有点沿着某一固定方向(或其反方向)运动，生成的轨迹才是直线．因此要说明一次函数图象是一条直线不妨说明图象上点动态生成的方向相同或相反．其次，从直线的倾斜角入手，挖掘理解一次函数图象是一条直线的突破口．事实上，要说明点动态生成的方向固定不变(或相反)可说明其运行轨迹与某一定直线平行(或所成的角相同)，即图象上任意一点与它经过的某定点的连线与一已知直线平行(或所成角为定值)．由直线的倾斜角定义可知，一次函数图象上任意一点和它与x轴交点的连线，与x轴正方向所成角相同(或互补)，由此可知一次函数的图象上的点确在一条直线上．这也正体现了“一次函数解析式y=kx+b中的k确定直线的方向和b确定了直线的位置”的本质．当然，教学中不必指出倾斜角一词，以免造成学生理解上的难度，增加不必要的负担．最后，从取点验证入手，找准完善一次函数图象是一条直线的着力点．前面两点只是说明了一次函数的图象上的点在一条直线上，那么是否这条直线上所有的点都在一次函数的图象上(即直线上所有点的坐标都满足一次函数y=kx+b的关系式)？当然要讲清此点必须借助于直线的斜率k，但这显然超出八年级学生的认知水平和理解能力，不宜过度拓展．教学中可以渗透为着力点，一方面通过学生找出直线上的部分整数坐标点坐标一一验证(或借助几何画板找非整数坐标点验证)，另一方面不妨从x可取一切实数和点的动态生成入手，说明一次函数的图象和描出的直线完全重合，以培养学生思维的严谨性．

笔者基于上述理解，在教学实践中进行了大胆的尝试，设计出“创设情境、大胆猜想、作图感知、画板验证和合情推理”等探究性教学流程，取得了可喜的效果．现不揣浅陋，一一分享，以求抛砖引玉．

2　教学设计

2．1创设情境，感知直线

新课伊始，学生观看某商场顾客乘坐自动扶梯自下而上的视频，并通过下列驱动问题引导学生思考、尝试和探究，从而感知一次函数的图象是一条直线．

问题1视频中，顾客头顶的蝴蝶结(视作一点)运动的路线是什么?(线段)

问题2你能说明为什么是线段吗？(蝴蝶结运动的方向始终与扶梯平行或与水平线夹角为定值)

设计说明问题1和问题2意在让学生从一个熟悉的生活实例中抽象出点动成线的事实，并理解点必须沿着一个固定的方向或其反方向运动，轨迹才是一条直线，从而为后面说明一次函数的图象是一条直线奠定理论基础．

2．2大胆猜想，引出直线

问题3若自动扶梯的高度为4.5米，其铅直方向上升的速度为每秒1米，顾客身高为1.5米．设顾客在自动扶梯上运行的时间为x秒、顾客头顶蝴蝶结离下楼面的高度为y米，请写出y关于x的函数关系式．(y=x+1.5，0≤x≤4.5)

问题4你能猜想出一次函数y=x+1.5在直角坐标系中的图象是什么吗？(一条直线)

设计说明问题3意在把现实中点运动的轨迹与一次函数图象建立联系，也为问题4的猜想和下一步作函数图象做好铺垫；问题4意在引导学生从具体到抽象、从部分到整体的迁移．当然，问题4的猜想是否正确尚需进一步验证和推理，教师可顺势引导学生进入下一环节的学习．

2．3动手操作，体验直线

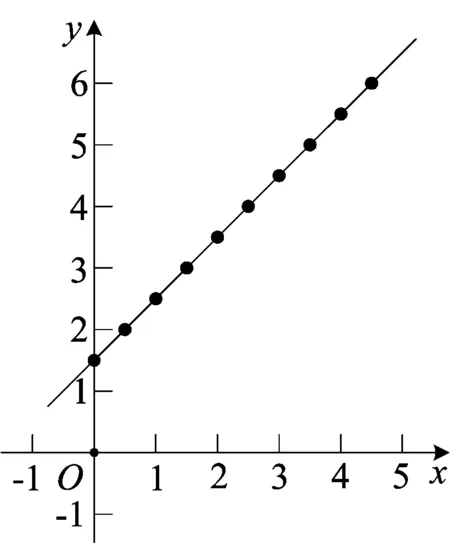
图1

通过“列表、描点和连线”三个步骤引导学生在平面直角坐标系中画出一次函数y=x+1.5的图象(如图1)，并启发学生思考：

问题5请问蝴蝶结运行的轨迹与图1之间有什么联系？(若以自动扶梯的下底部为原点，沿扶梯运动的水平方向为x轴正方向建立直角坐标系，则顾客头顶运行的轨迹是图1中图象的一部分)

问题6除了描出的点外，直线上的其他点的横、纵坐标是否依然满足一次函数y=x+1.5的关系式？(引导学生通过作图找出x取特殊点时对应的纵坐标，并计算验证)

问题7会不会有横、纵坐标满足y=x+1.5的点不在这条直线上？(引导学生再描一些点加以验证)

设计说明通过问题5引导学生进一步挖掘顾客头顶的蝴蝶结运行轨迹与对应一次函数图象之间的关联性，突出部分与整体的关系，强化直线是向两方无限延伸的；问题6和问题7意在让学生初步体验自变量x取值的纯粹性和完备性，以及图象上点的连续性，加深对函数图象概念的理解，为今后进一步学习曲线与方程奠定基础．同时，问题6与问题7也点破学生心中的疑虑，从而把思考引向深入，并自然转入下一环节的教学．

2.4动态演示，验证直线

对于问题6与问题7而言，上述验证中描点个数毕竟有限，很难一下子消除学生心中的疑虑．但若能借助几何画板动态生成的优越性，巧妙地把所描点化少为多、化有限为无限，则可有效消除学生心中的疑虑，起到直观验证之效．为了便于读者操作，现把作图方法也一并呈现，以供参考．

2.4.1作图流程．

步骤1新建一个画板文档，在绘图区域内，做一条水平射线AM，竖直射线AN，在水平射线AM上任取两点B、C，用点B来控制列宽，点C来控制自变量的个数；在竖直射线AN上任取点D，用点D来控制行高；

步骤2标记向量AD，选定点B，平移得到点B′，构造线段AB、AD、DB′、BB′，隐藏射线；把线段AB向下平移向量DA，得到线段A′B′构造线段BB′；

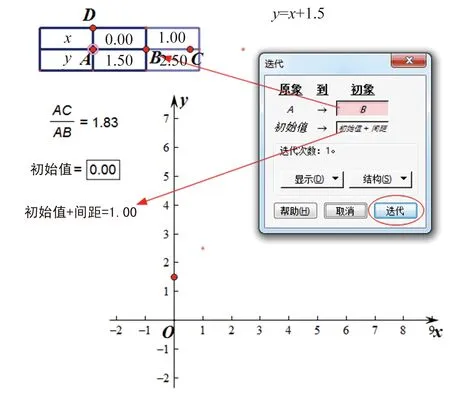
图2

步骤4新建参数1，参数名称改为初始值，值为1.00；新建参数2，名称改为间距，值为1.0；新建参数3，名称改为k，值为1；新建参数4，名称改为b，值为1.5；

步骤5选定初始值与间距这两个参数，分别做计算：初始值+间距；k×初始值+b；选定初始值，选择数据菜单中的计算，得到计算后的初始值；

步骤6建立平面直角直标系，绘制点(初始值，k×初始值+b)；

步骤7选择第5步计算后的初始值合并到上方表格的中心作为自变量x的值，把步骤5的第2个计算值合并到下方表格的中心作为因变量y的值．

2.4.2画板演示．

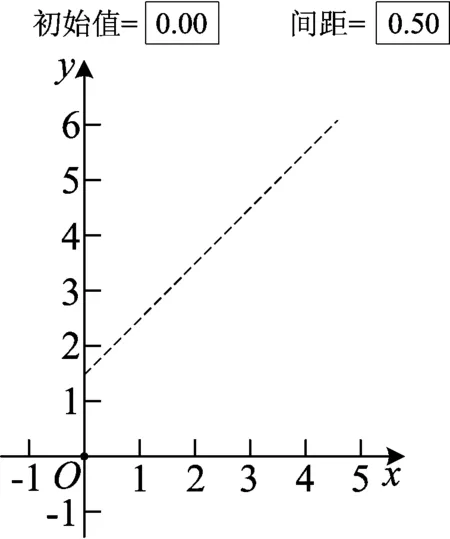
图3

图4

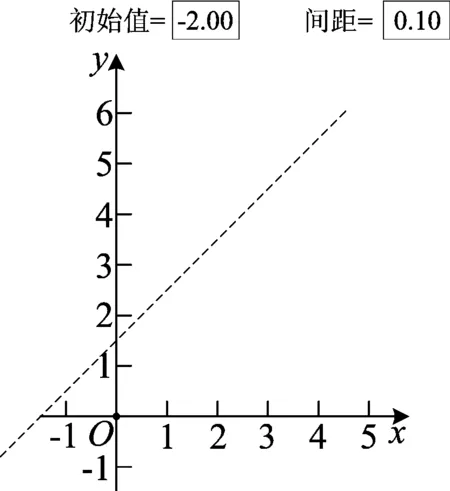
图5

演示1把初始值和间距这两个参数的值分别设置为0.00和0.50，并且取10个自变量，则可得图3中的10个点．

演示2把自变量的初始值仍设置为0.00而间距设置为0.30，同是拖动图2中的点C增加自变量个数，则在10个点之间增加许多点，图象的直线感也增强了(如图4)．

演示3如果间距缩小为0.10，同时为增加点的个数，拖动图2中的点B缩小表格的宽度，则效果就更加明显了.

演示4把自变量的初始值设置为-2.00而间距设置为0.10不变，继续拖动点C增加自变量个数，则不仅原有10个点之间点数增加而且点向外拓展，直线感更逼真了(如图5)．

不难想象，随着初始值趋向于-∞且间距趋向于0，一条直线便活灵活现地展示在学生的眼前，他们心中的疑虑瞬间也会荡然无存了．

2.5合情推理，理解直线

由情境可知，点动成线，但点运动的轨迹若为一条直线则必须要沿着某一固定的方向(或其反方向)运动．具体理解可说明其满足两点：其一，经过某一定点(确定直线所在的位置)；其二动点与该定点的连线与某一定直线平行或所成角为定值(确定点运动的方向)．鉴于此，为了进一步从理论上说明一次函数y=x+1.5的图象确为一条直线，特作如下设计：

问题8一次函数y=x+1.5的图象与x轴的交点A的坐标是什么？(A(-1.5，0))

问题9在“动手操作、体验直线”环节中所描的点中任取三点B、C、D，把它们分别与A点连接，请问AB、AC、AD与x轴正方向所成的角分别为多少度？(135°或45°)

问题10设P(x，x+1.5)为一次函数y=x+1.5图象上任一点，猜想PA与x轴正方向所成角的度数，并说明理由．(135°或45°)

设计说明问题8意在引导学生找出定点，确定直线所在的位置；从问题9到问题10突出了由特殊到一般的思维过程，主要目的在于引导学生发现坐标满足解析式y=x+1.5的其他点与A点连线的方向不变性(相同或相反)，从而推理出“一次函数y=x+1.5的图象是一条过(-1.5，0)点且与x轴夹角为45°的直线”．对于问题10可引导学生过点P作PQ⊥x轴于Q，通过△PQA为等腰直角三角形加以证明．显然，有了上述问题的探究，学生对一次函数y=x+1.5的图象是一条直线的认识就有了理论上的理解与支撑，必然也就深信不疑了．

2.6两点画线，回归本质

问题10既然一次函数的图象是一条直线，那么能否快速准确地画出一次函数y=kx+b的图象呢？依据是什么？(依据“两点确定一条直线”，可在直线上任取两点画出一次函数的图象)

设计说明通过“两点画直线”既突出一次函数图象的本质，又彰显了数学的简洁美．而问题11更凸显了一次函数图象上特殊点的重要性．

3　两点思考

3.1如何灵活处理教材

对教材的灵活性使用可谓仁者见仁、智者见智，目前的着力点普遍于“材料选补”、 “结构调整”、“情景创设”和“过程再现”上，笔者认为“对知识结构的重新梳理和内容潜在功能的深入挖掘”也不容忽视．

教材中对一次函数的图象及性质教学只安排了两课时，第一课时主要作图象并根据图象观察一次函数的性质，第二课时主要研究图象的增减性及其应用．但多年实践证明：第一课时中对用描点和观察得出一次函数的图象是一条直线的处理方式学生是心存疑虑的，有强加之感，并未从本质上加以揭示．因此把两课时拆为三课时，第一课时主要通过“一点尝试”中的五个环节，逐步引导学生“感知、体验、验证、理解和揭示”一次函数图象是一条直线，深入挖掘其本质，力求做到“用而不疑”，为其性质的学习和运用奠定了良好的基础．另外，如此处理对培养学生数学思维的严密性和一丝不苟的探究精神也大有裨益．

3.2如何凸显新课程的理念

新课程倡导：通过学生活动来突出学生学习的主体性，且在新知学习上，往往从实例引入抽象出数学模型，再通过观察、分析、比较、归纳，探究知识的发生、发展、形成的过程，得出结论，并运用于解决实际问题，强化能力培养．因此，教学过程中，如何安排学生的学习活动至关重要．本节课，设计了三个方面的学生活动：一是通过画函数图象感知一次函数图象的形状；二是通过几何画板演示验证一次函数的图象；三是探究一次函数的图象与 k、b 的关系，揭示本质．不仅让学生知道学什么，更知道如何学，为什么这样学．在方法上“授人以渔”，为学生的终身发展奠定良好的基础．

当然如何理解一次函数的图象为一条直线是教学难点，但不能因为是难点，教学中就采取回避的策略．相反若能象本文所设计一样，基于引导学生理解之上，并结合实际情况，大胆实施因材施教，积极寻求突破对策，才是积极处理教学难点的科学态度．

1浙教版义务教育教科书八年级上册：数学.杭州：浙江教育出版社，2013

2王耀．例谈反比例函数图象的旋转变换及其应用 [J]．中学数学教学，2014(2)

2016-06-18)