对2016年高考四川卷第15题的研究

北京市丰台二中

甘志国　　(邮编：100071)



对2016年高考四川卷第15题的研究

北京市丰台二中

甘志国(邮编：100071)

①若点A的“伴随点”是点A′，则点A′的“伴随点”是点A；

②单位圆上的点的“伴随点”仍在单位圆上；

③若两点关于x轴对称，则它们的“伴随点”关于y轴对称；

④若三点在同一条直线上，则它们的“伴随点”一定共线.

其中的真命题是______(写出所有真命题的序号).

①若点A的“伴随点”是点A′，则点A′的“伴随点”是点A；

②单位圆的“伴随曲线”是它自身；

③若曲线C关于x轴对称，则其“伴随曲线”C′关于y轴对称；

④一条直线的“伴随曲线”是一条直线.

其中的真命题是______(写出所有真命题的序号).

这两道高考题是一对姊妹题，下面只对后者做详细解答和研究.

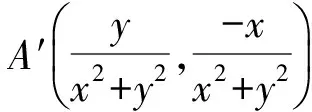
所以点A′的“伴随点”是(-x，-y)，得①错误．

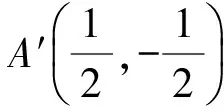
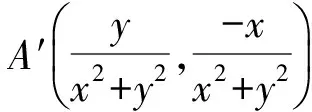
下面再对高考题2作研究.

设点P(x，y)的“伴随点”为P′(u，v).

当x2+y2=0即x=y=0时，得P′(0,0).

下面只证⟸：若x2+y2=0，得x=y=0，再得u=v=0,u2+v2=0，与题设u2+v2≠0矛盾！所以x2+y2≠0.

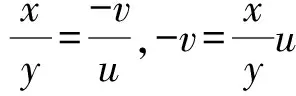
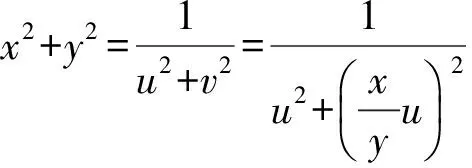
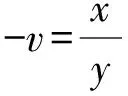
由此可证得下面的结论.

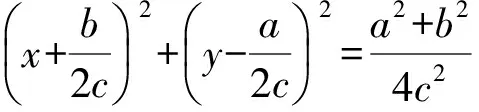
证明设直线ax+by+c=0上的点P(x，y)的“伴随点”为P′(u，v).

当x2+y2=0时，得P′(0,0).

此时，由点P(x，y)在直线ax+by+c=0上，可得

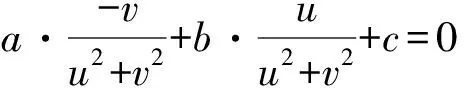
c(u2+v2)+bu-av=0(u2+v2≠0).

进而可得欲证结论成立.

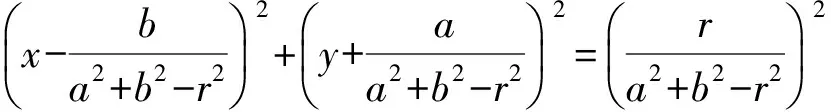
证明设圆(x-a)2+(y-b)2=r2上的点P(x，y)的“伴随点”为P′(u，v).

当x2+y2=0时，得P′(0,0).

此时，由点P(x，y)在圆(x-a)2+(y-b)2=r2上，可得

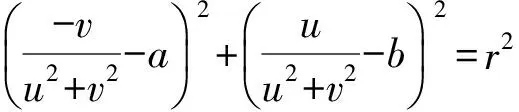
(u2+v2)[(a2+b2-r2)(u2+v2)-2bu+2av+1]=0(u2+v2≠0),

(a2+b2-r2)(u2+v2)-2bu+2av+1=0(u2+v2≠0).

当圆(x-a)2+(y-b)2=r2过坐标原点即a2+b2-r2=0时，可得欲证结论成立；当圆(x-a)2+(y-b)2=r2不过坐标原点即a2+b2-r2≠0时，可得欲证结论也成立.

所以欲证结论成立.

推论(1)单位圆的“伴随曲线”是自身；

(3)圆(x-a)2+(y-b)2=a2+b2的“伴随曲线”是直线2bx-2ay-1=0及坐标原点组成的图形.

2016-07-23)