2016年高考四川卷解析几何压轴题的五种求解视角

四川省资阳市外国语实验学校

蔡勇全　　(邮编：641300)



解题方法

2016年高考四川卷解析几何压轴题的五种求解视角

四川省资阳市外国语实验学校

蔡勇全(邮编：641300)

1　试题再现与评价

(Ⅰ)求椭圆E的方程；

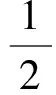
这道题目是2016年高考四川卷文科第20题，属于解析几何压轴题，笔者有幸参与了本次试卷评阅工作，从试卷布局、试题难度以及评阅结果等情况分析来看，本题是整套试卷的压轴题之一，尤其是第(Ⅱ)小问，放弃不做、胡乱书写以及找不到解题突破口而导致得分率较低的现象比比皆是，究其原因，在于该题第2小问综合性强，解法灵活多样，涉及的知识点较多，要求的运算能力较强，对学生的解题技能提出了较高的要求.

2　多视角求解

(Ⅱ)下面从五种视角探讨本题第(Ⅱ)小问的求解策略，供大家参考.

视角1 借助两点间距离公式及韦达定理

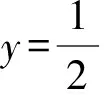
评注判别式与韦达定理虽是代数基础知识，但却是求解解析几何问题的利器与法宝，尤其是在解答直线与圆锥曲线相交问题时，其作用往往不可小觑.

视角2 借助点差法、韦达定理及两点间距离公式

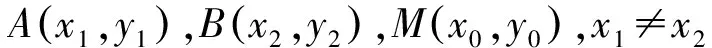
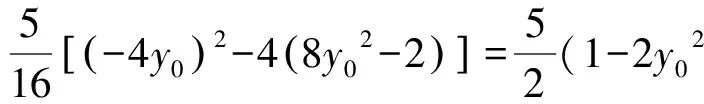
评注利用点差法直接找到了点M的横、纵坐标之间的关系，避免了出现视角1中先利用中点坐标公式求得点M的横坐标，再代入直线l的方程求得点M的纵坐标的运算过程，显得简捷高效.

视角3借助向量的两种运算及韦达定理

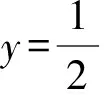
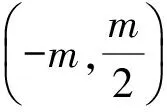
评注引入向量并借用其两种运算形式，可以使几何问题代数化，达到事半功倍的解题效果.

视角4借助直线参数方程、韦达定理及两点间距离公式

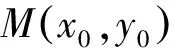
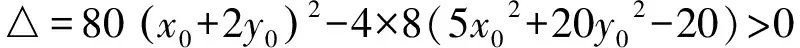
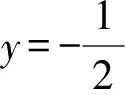
评注利用直线或曲线的参数方程解决解析几何问题，可以极大地简化运算、减少运算量，实现快速解题的效果.

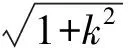
视角5借助弦长公式及韦达定理

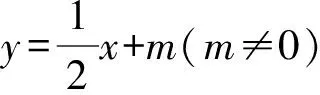
3　解题启示

众所周知，运算量大是解析几何问题的突出特点，而运算量大的根源在于此类题目必然出现直线与曲线或曲线与曲线具有某种位置关系这一条件.但从如上案例的多种求解思路不难看出，抓住代数知识中的韦达定理应是求解此类问题的必经之路.同时抓住几何内容中的参数方程、弦长公式以及实现代数与几何相互转化的向量工具等知识，共同构成简化运算、高效解题的不二法门.因此在平时的教学中，我们应把这些知识、方法的掌握真正落到实处，为提高解题的有效性提供必要的保障.

2016-07-01)