船舶十字轴万向节轴系受力分析

陈俊义 仲伟国 栾 军

（张家港市久盛船业有限公司 张家港215600）

船舶十字轴万向节轴系受力分析

陈俊义 仲伟国 栾 军

（张家港市久盛船业有限公司 张家港215600）

船舶十字轴万向节轴系的轴承由于十字轴万向节的影响，其受力情况复杂。文章简要分析十字轴万向节特殊的力学特性和速度特性，并分析十字轴万向节的受力情况。在此基础上运用平衡方程、三弯矩方程、MATLAB软件和EXCEL软件计算船舶十字轴万向节轴系上各个轴承在各种情况下的径向负荷。最后，简要分析十字轴万向节轴向力计算方法及其对轴系轴向力轴承的影响。为十字轴万向节轴系设计、建造和维修提供理论依据。

十字轴万向节 ；平衡方程；三弯矩方程 ；轴承 ；负荷

引 言

船舶360°全回转舵桨装置由于其结构紧凑、操纵灵活和维修方便等原因被广泛运用于港作拖轮和工程拖轮上（见下页图1）。由于舵桨装置的输入轴和作为船舶主动力源的柴油机难以布置在同一条直线上，通常需要十字轴万向节轴系将其连接在一起（见下页图2），而这个十字轴万向节轴系则由十字轴万向节、短轴、中间轴和高弹性联轴节等设备组成，其中十字轴万向节是关键设备，起到改变轴系角度的作用。十字轴万向节由于自身特殊的结构型式使其在传递功率时具有特殊力学特性和速度特性，这两方面的特性使十字轴万向节轴系上各个轴承的受力情况比一般传动形式的轴承受力情况复杂。在此，我们通过对十字轴万向节这两方面特性分析来研究其这种特性对轴系上各轴承的影响。另外，周期性的轴向力也是十字轴万向节在传递功率时特有的，我们在此分析其产生的原因、计算方法及对轴承的影响。

图1 船舶十字轴万向节推进轴布置图

图2 十字轴万向节推进轴系图

1 十字轴万向节受力分析

十字轴万向节的结构如图3所示，其十字轴主动轴叉和从动轴叉运行轨迹及相互之间的几何关系如下页图4所示。

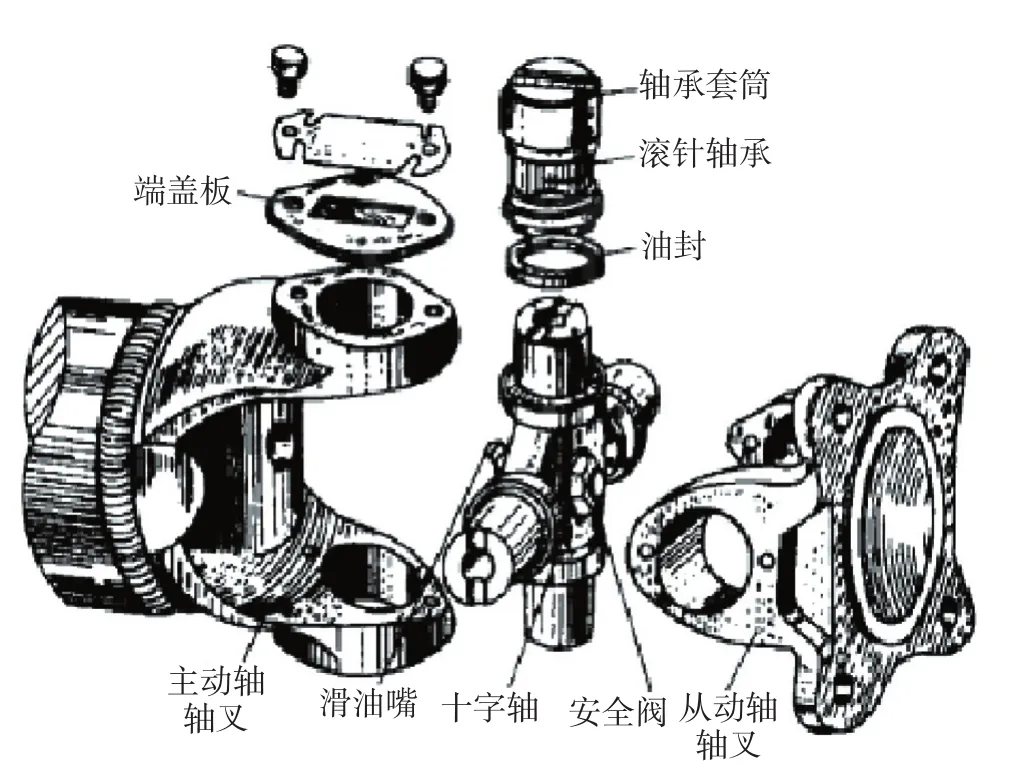
图3 十字轴万向节结构图

图4（b）中表示的是两个轴叉与十字轴接触点的传动平面图形。当主动轴如图中所示的方向旋转时，主动轴的上下两个轴叉通过十字轴带动从动轴（叉）旋转，主动轴轴叉和十字轴的接触传力点在垂直于主动轴的平面内做旋转运动；从动轴轴叉和十字轴的接触传力点在垂直于从动轴的平面内做旋转运动。主动轴和从动轴夹角为α。

图4 十字轴万向节运行轨迹及几何关系图

在图4（b）中，当主动轴叉由D点运动到E点时，设∠DOE = β1，同时，从动轴叉由A点运动到C点，设∠AOC = β2。因C点和E点都是相邻两轴叉和十字轴的传力接触点，所以OE和OC都等于十字轴的半径R，∠COE=∠AOD =90°，所以有

建立图4（b）中所示的空间直角坐标系，分别求出点C和E的坐标：C（R·sin β2· sinα，R·cos β2，R·sin β2·cos α）、E（0，-R·sin β1，R·cos β1），然后利用空间解析几何中的两点间距离公式：

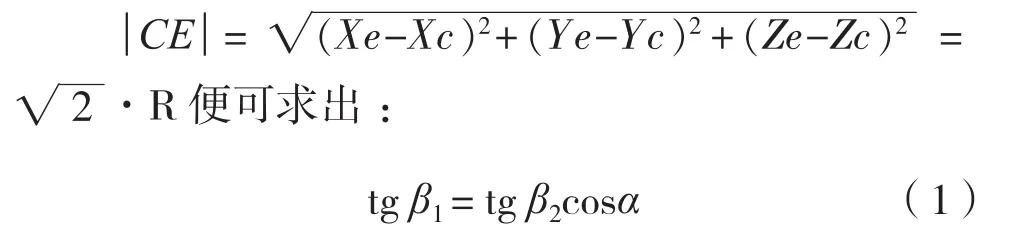
在轴系运转时，当十字轴万向节输入端转速恒定，十字轴万向节中的十字轴就会处于动态平衡中。于是，图4（c）中的x、y和z坐标上都有：∑F=0；∑M=0。结合公式（1），可以求出：

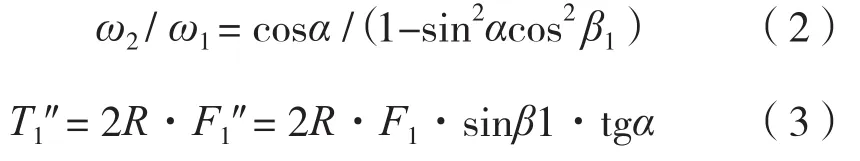
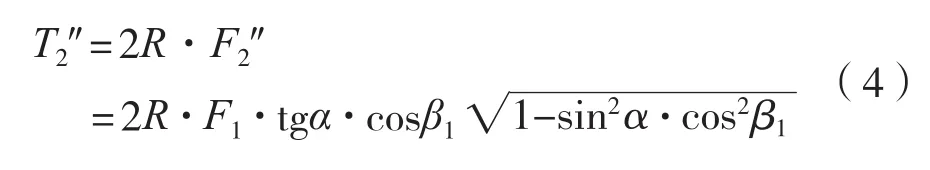
图中和式中：T1（T1= 2R·F1）、T2（T2= 2R·F2）为十字轴万向节主动轴叉和从动轴叉产生的力矩（N·m），分别在主动叉运行轨迹和从动叉运行轨迹内，且分别垂直于OE和OC； T1″ 和T2″ 分别为主动轴和从动轴附加力矩（N·m），分别垂直于在主动叉运行轨迹和从动叉运行轨迹，且分别垂直于OE和OC；T1′（T1′= 2R·F1′）和T2′（T2′= 2R·F2′）为主动轴叉和从动轴叉合力矩（N·m），且T1′= T2′，方向相反。

式（2）就是万向节的速度特性公式，它表明万向节主动轴和从动轴转速不是线性关系的。式（3）和（4）是十字轴万向节的力学特性公式，它表明十字轴万向节的十字轴在运转中要保持平衡，就必须存在另外两个附加力矩T1″ 和T2″ ，见图4（c）。

在十字轴万向节推进轴系中，常采用两个十字万轴向节串联，中间用花键连接而组成双十字轴万向节的型式，见下页图5（a）。之所以采用这种型式，是因为如果第一个万向节的主、从动轴夹角α1等于第二个万向节的主、从动轴夹角α2，见图5（b），则由式（1）可知，双十字轴万向节的输入转速等于输出转速。这样的设计使得中间轴、舵桨装置的转速和力矩可以分别等于柴油机的输出转速和力矩。

图5 双十字轴万向节

2 十字轴万向节轴系径向受力分析

2.1 轴系计算模型

万向节的力学特性公式表明，万向节在传递功率时在万向节处会存在一个附加力矩，该附加力矩会对十字轴万向节轴系内各个轴承的受力情况造成影响。下面，我们以图2所示的十字轴万向节轴系为模型，计算各轴承在各种情况下的受力大小，以此来了解万向节的力学特性对轴系内轴承的影响。

如图2所示轴系中的万向节，由于其形状复杂，所以较难确定各部分重心的位置，计算复杂。在不影响计算结果的前提下，我们将其简化成重力均匀的几何形状，与主机连接的高弹性联轴节和轴系各个联轴节同样作如此简化。这样，最终得到如图6所示的计算模型。在这个模型中，将轴系分为4段来计算轴承的径向受力大小。

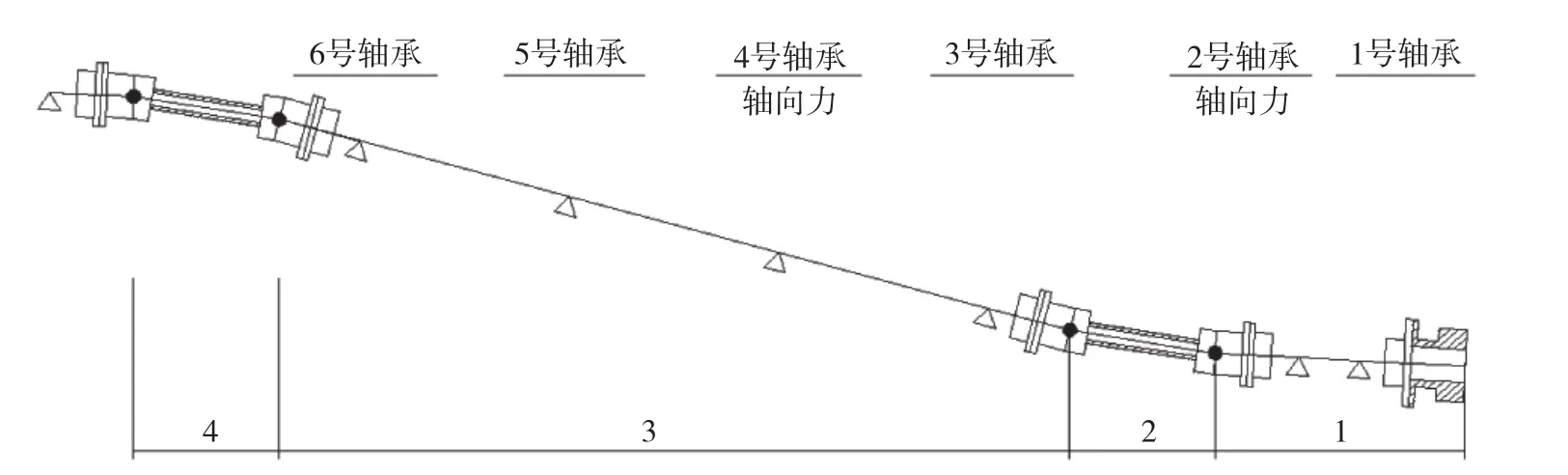
图6 十字轴万向节轴系计算模型

2.2 轴系计算方法

首先来了解十字轴万向节处的受力情况。

在图7（a）的简单轴系中，m-m截面为万向节联接。沿m-m截面把轴系分成主动轴、十字轴和从动轴，见图7（b）。在分析万向节的受力时，假设M1为十字轴作用于主动轴叉上的弯矩，M2为十字轴作用于从动轴叉上的弯矩。但是显而易见，M2这个弯矩不可能存在，因为从动轴叉和十字轴的接触传力点可以相互旋转，所以，十字轴不可能对从动轴叉产生这个弯矩。同理M2′也是如此。这样根据平衡方程∑F=0、∑M=0，M1和M1′也不存在。也就是说，在万向节处，只有剪力F的存在，而弯矩是不能通过万向节从主动轴传递到从动轴中去的。

图7 十字轴万向节受力简图

如果该轴系传递功率，且主动轴、从动轴的夹角α不为零，由第1节分析知道在主动轴叉和从动轴叉处还存在附加力矩T1″和T2″。这样主动轴叉受到剪力Fa和附加力距T1″的作用［见图7（c）］，从动轴叉受到剪力Fb和附加力矩T2″的作用（当然还有力矩T1和T2等，这些力矩对下面的分析没有影响，不予讨论）。

下面介绍图6中各段轴的径向受力计算方法。

2.2.1 第2段轴计算方法

在图8（a）中Fa和Fb为双十字轴万向节两端轴系对它的力，假定它们的方向如图所示；T2″为万向节在传递功率时的附加力矩［附加力矩T2″见式（4）］，图中的方向为实际力矩方向。重力单独依据平衡方程求出，后面再分析。

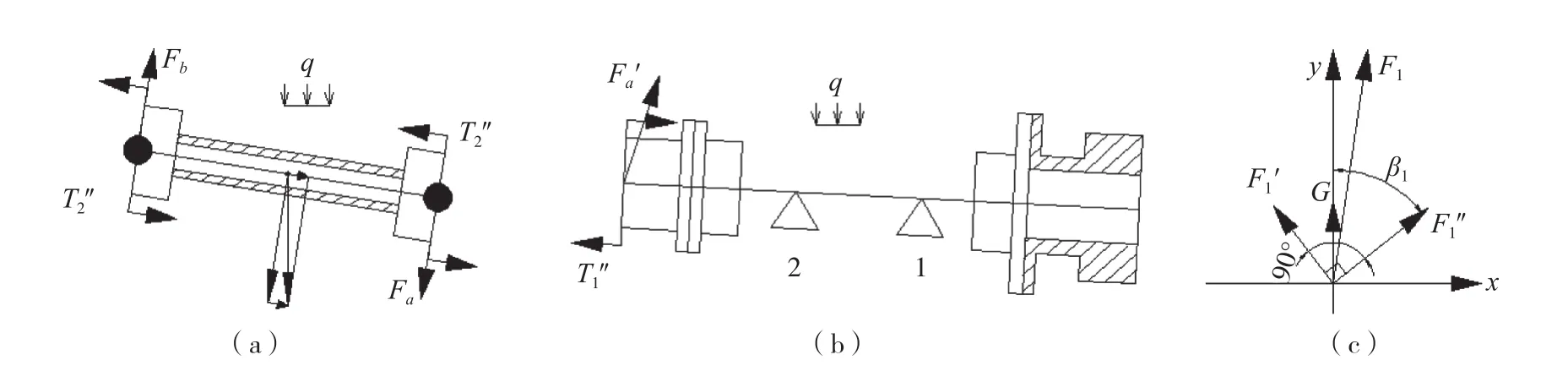
图8 第1、第2段轴垂直方向受力简图和1号轴承综合受力图

知道柴油机输出功率和转速后，可以由公式T = 9 549·P/n求得T（式中参数的物理意义及量纲分析见参考文献［1］），再知道公式（4）中的β1和α后，就可以求出T2″。然后，根据平衡方程∑F = 0、∑M = 0，求出Fa和Fb的大小及方向。Fa和Fb的大小及方向与T2″有关，而T2″的大小和方向是变化的，因此，Fa和Fb不含重力的因素在内，重力由平衡方程∑F = 0和∑M = 0单独求出。

2.2.2 第1段轴计算方法

图8（b）中，该段轴受到3种力的作用，分别是：万向节附加力矩T1″；第2段轴对它的反作用力Fa′（与第1段轴中的Fa大小相等，方向相反）和重力作用。这三个力中，只有重力是不变的，其他两个力的大小和方向是随旋转角度的改变而改变的，且作用面不在同一平面上，成90°。因此，不能将它们放在一起来求解，需要将它们分开，根据平衡方程∑F = 0；∑M = 0单独求出在T1″、 Fa′和重力（含前段轴重力对它的作用）作用下的1号和2号轴承受力F1和F2，最后求出各自的合力（类似的计算见参考文献［2］）。

1号轴承在角β1时，受力见图8（c）：图中G为第1段和第2段轴重力分量单独作用下1号轴承的支反力； F1′为Fa′单独作用下1号轴承的支反力；F1″为 T1″独作用下1号轴承的支反力。F1为G、F1′、 F1″的合力。由图中可见，F1″的作用方向与垂直线的夹角为β1，F1′的方向与F1″的方向的夹角为90°。显然，F1′和F1″的作用方向都是随β1变化而变化的，合力F1的作用方向也是随着β1变化而变化的。

2.2.3 第3段轴计算方法

用同样方法可以求出图9中Fb′、Fc′、Tb和Te。但是，该段轴系含有四个轴承，为超静定结构，在此可以用三弯矩方程来计算该轴系各个轴承的受力大小。

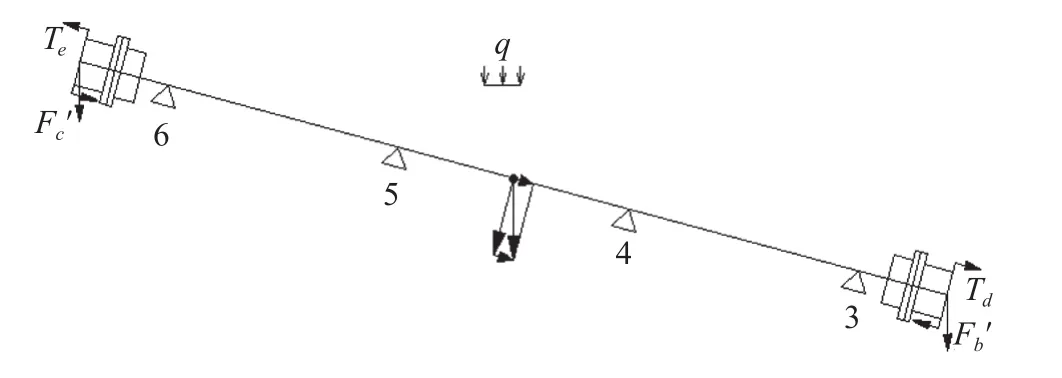
图9 第3段轴垂直方向受力简图

三弯矩方程如下：

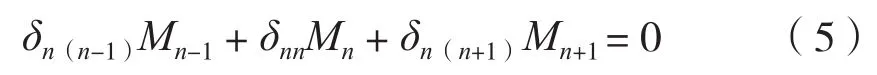
式中：δn（n-1）、δnn、δn（n+1）分别为单位弯矩作用在点n-1、n、n+1时，点n-1、n、n+1两边的相对转角；Mn-1、Mn、Mn+1为点n-1、n、n+1上的弯矩，N·m。具体参数物理意义及量纲分析见参考文献［3］。

我们运用三弯矩方程列出多元一次方程组，然后用MATLAB软件和EXCEL软件计算这个方程组，并求出各个轴承在各种情况下的受力大小。最后用EXCEL软件自动生成图形文件用于分析。

这里还要提到一点：根据式（2）可知，在输入转速ω1一定的情况下 ，输出转速ω2是变化的。这样在图5（a）中两个十字轴之间的部分的速度是变化的，也就是存在角加速度。由此产生轴系转动时，两个十字轴之间的部分存在一个转动惯量的问题（转动惯量的计算见参考文献［4］）。根据计算结果，发现这个转动惯量对后面的分析和结论都没有影响，这里就不作详细讨论了。

2.3 各种功率时轴承的负荷计算及分析

轴系传递各种功率时的轴承负荷计算结果见图10。图中可见：（1）各轴承在轴系静止时的负荷大小与轴系在传递功率时的轴承负荷大小相差很大，由此可知：十字轴万向节引起的附加力矩对轴承负荷影响很大，传递功率越大，影响越大。这与实际情况是一致的，实船上柴油机低转速空载时的轴承温度要比柴油机在额定转速、额定功率时的轴承温度要低得多；（2）各轴承在轴系传递功率时的负荷大小都是周期性的，其周期为180°。在一个周期内，每个轴承合力F都有一个最大值和一个最小值。

2.4 轴承受力方向变化分析

图10所示的计算结果显示的仅为轴承负荷大小上的变化，而实际上，轴承受力方向也是变化的。在图8（c）中，F1″和F2″的大小和方向是随着旋转角度不同而变化的，因此，综合受力方向是随着旋转角度不同而变化的。图11表示2号和6号轴承综合受力方向变化的情况，图中可见：2号轴承受点变化比6号轴承复杂的多。另外，1号轴承的受力点变化与2号轴承类似，3号、4号和5号轴承的受力点变化与6号轴承类似。

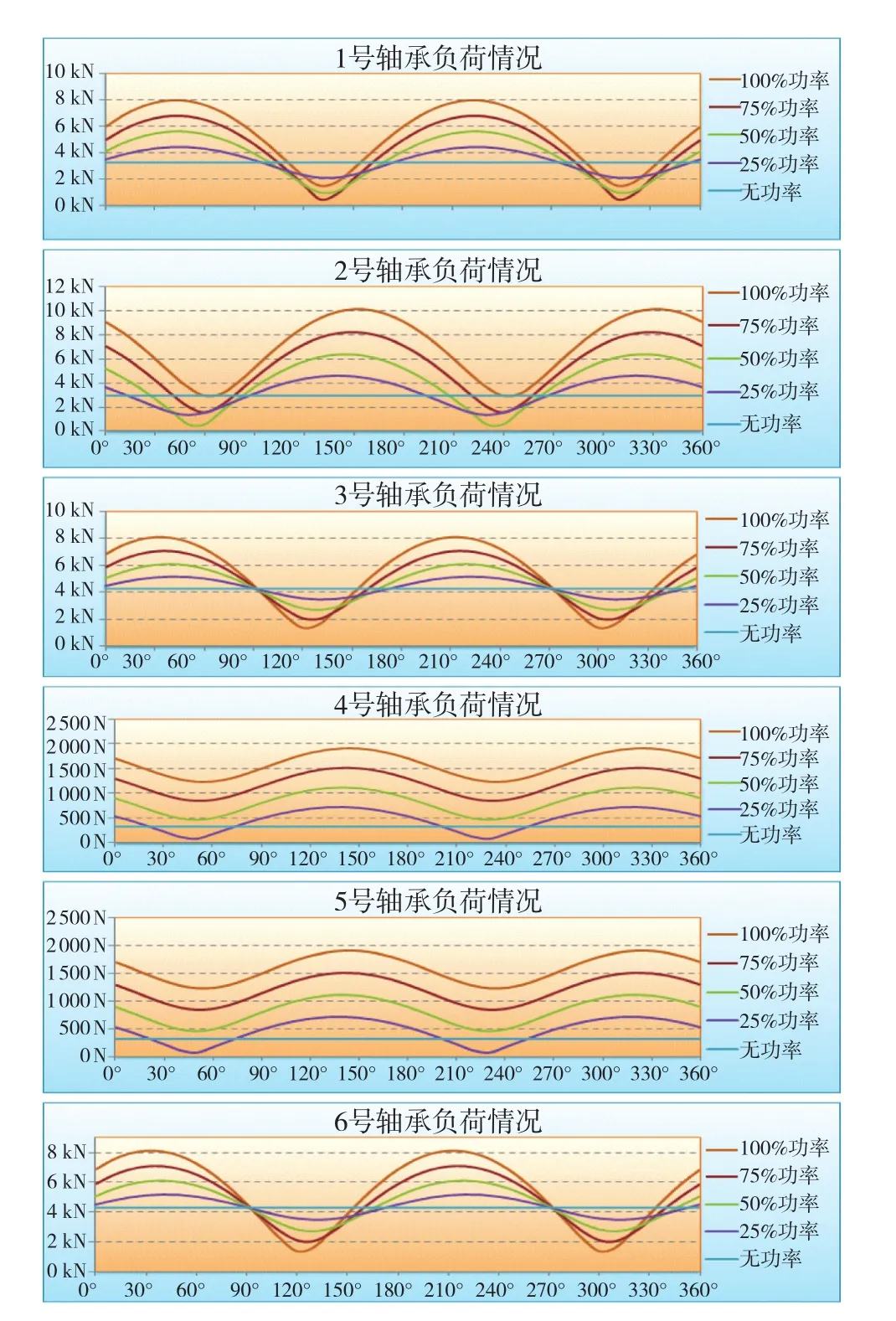
图10 轴承在各种功率时的负荷计算结果

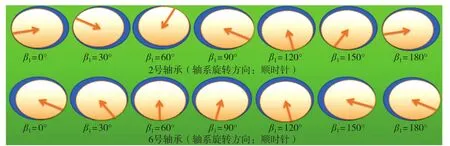
图11 2号和6号轴承的综合受力点变化示意图

2.5 主动轴和从动轴夹角α 对轴承的负荷影响

由上述分析可知：万向节主动轴和从动轴夹角α的大小对各轴承的负荷有影响，图12是2号和6号轴承在不同的α夹角时的负荷变化情况。由图9可知：α角度越大，万向节附加力的影响越大。该结论与实船上情况相同，在实船上，相同条件下α夹角为7°时的轴承温度高于α夹角为6°时的温度。

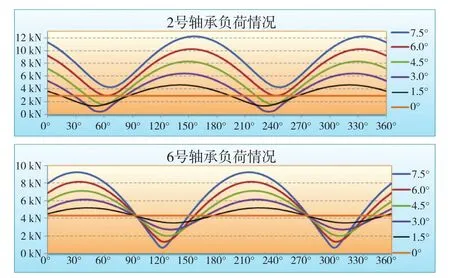
图12 2号和6号轴承在各α夹角时的负荷计算结果

2.6 两个万向节错位的影响

轴系各轴承在传递功率时的负荷大小受到两个万向节的影响，会出现周期性的变化。如果将2号双十字万向节相对于1号双十字万向节偏转一个角度安装，会产生什么样的结果呢？图13为3号～6号轴承在100%功率时两个万向节不同安装角度轴承的负荷计算结果。（1号和2号轴承不会受到两个双十字万向节错位的影响）。由图13可见：两个双十字万向节错位90°安装对4号和5号和6号轴承负荷影响较大，3号轴承负荷几乎没有变化。同时也可以看出：没有错位安装对轴系四个轴承的影响比较有利。

2.7 轴承位移偏差的影响

轴系3号至6号轴承在实船建造和维修时，由于安装或船体刚度的原因会产生位移偏差（即四个轴承的中心不在一条直线上），这样也会对轴承的负荷造成影响（1号和2号轴承不存在这个问题）。在此，需要在三弯矩方程式的左边增加一项位移偏移系数K来计算分析位移偏差的影响（关于K的计算方法见参考文献［5］）。图14表示位移偏差对各轴承负荷的影响。

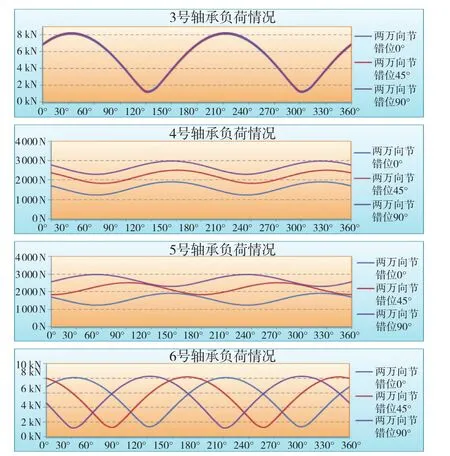
图13 1号和2号万向节在三种安装角度时轴承负荷计算结果

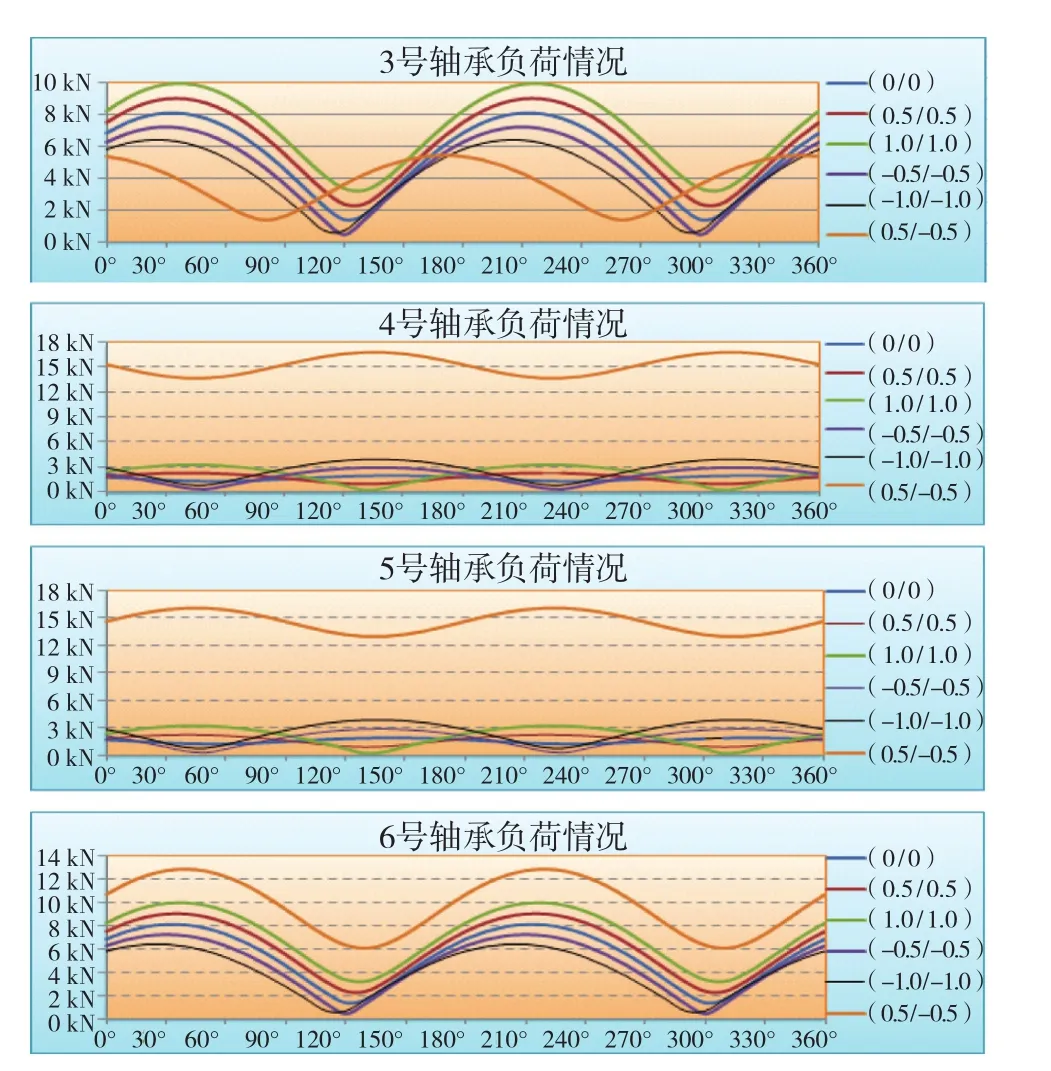
图14 4号和5号轴承垂直偏移情况下轴承负荷计算结果

图14中的（0.5/0.5）表示：5号和4号轴承分别相对3号和6号轴承所在的直线向下偏移0.5 mm，其他情况类似。从图中可以看出：（1）当5号和4号轴承偏移的数值越大，对各轴承负荷的影响也越大；（2）当5号和4号轴承两个轴承偏移的数值相差越大，对轴承负荷的影响越大，尤其是对4#和5#轴承［见（0.5/-0.5曲线）］。各轴承在水平方向有偏移时的负荷变化情况和此类似。由此，可以得出一个结论：中间轴各个轴承的负荷与船体结构的刚度有关系。船体刚度越小，在船舶运行中，轴承越容易偏离中心线位置，轴承负荷越容易变大。

2.8 两个万向节不同角度时的影响

船舶十字轴万向节轴系在设计时，通常两个万向节主动轴和从动轴夹角α都会同样布置，如果布置成不一样的角度，会有什么影响呢？图15为两个万向节不同角度的负荷计算结果。

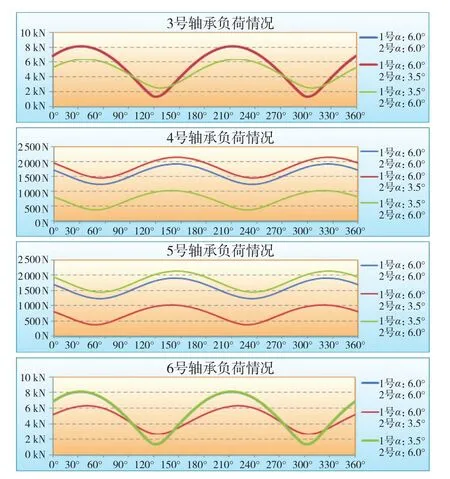
图15 两个万向节不同角度的负荷计算结果

图中3号轴承和6号轴承中线型较粗的曲线为两条重合曲线。从图中可见：

（1）3号轴承负荷只与1号万向节的角度有关，2号万向节的角度对它影响很小；6号轴承与之类似。

（2）两个万向节的角度对4号和5号轴承都有影响，离它们最近的万向节对它们影响大些。

3 十字轴万向节轴系轴向力的分析

十字轴万向节轴系螺旋桨产生的推力传递给舵桨，然后由舵桨传递给船体，因此这种轴系不需要设推力轴承。但这种轴系是倾斜布置的，它的重力沿着轴线方向会产生一个分力。万向节运转时产生的力与轴线并非垂直（如图8（b）中的Fa′），也会沿轴线产生一个分力。因此，这种轴系就需要有轴承来承受这两种轴向力，如2号和4号轴承（之所以设置两个轴承，是因为第1段轴和第3段轴之间的万向节是可伸缩的）。这两个轴承承受的轴向力如下：

2号轴承：由图可知，该轴承承受了第1段轴系重力的轴向分力作用、Fa′的轴向分力作用和1号双十字轴万向节的右边部分的重力的轴向分力作用。

4号轴承：计算要求与2号轴承类似。仅在计算万向节的重力时，需要计算1号双十字轴万向节的右边部分重力的轴向分力和2号双十字轴万向节左边部分的重力的轴向分力。

具体的轴向力计算结果见图16。

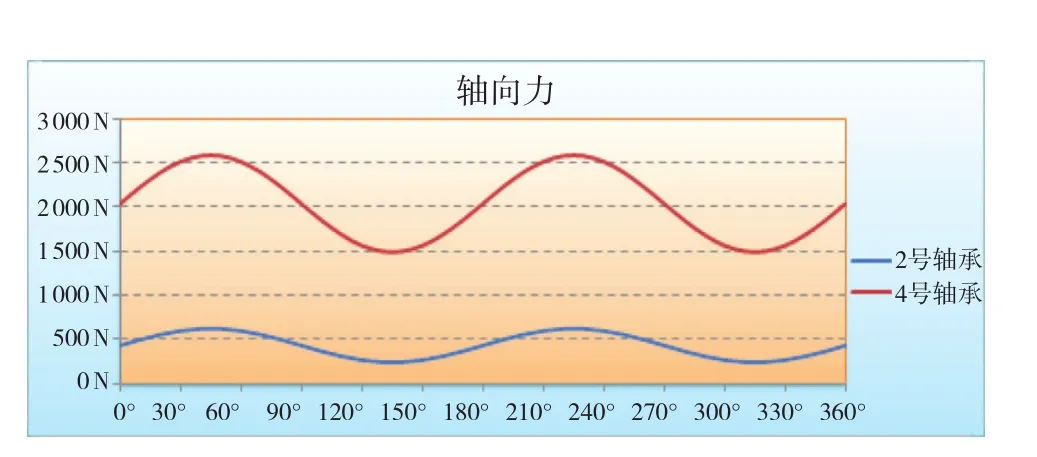
图16 轴向力计算结果

该轴系在实船运行过程中，经常会出现2号轴承发热的现象。从上述分析中可知：该轴承径向力是最大的，还要承受周期性的轴向力，所以很容易造成轴承运行过热；并且1号轴承径向受力比2号轴承径向受力小些，因此，将1号轴承作为短轴轴向力轴承是比较合理的。在实船上，将1号轴承作为轴向力轴承，在运行中，短轴上的两个轴承的温度都在可接受的范围内。

4 结 论

综上所述，十字轴万向节轴系在不同的传递功率、α夹角和万向节安装方式以及不同的轴承位移偏差情况下，对轴系相关的轴承负荷影响都很大，这表明十字轴万向节的速度特性和力学特性对轴系的影响很大。实践也表明，十字轴万向节的速度特性和力学特性会使轴系上的轴承产生振动与发热现象，从而使轴承受力点呈周期性变化。轴承负荷较大的周期性变化也使轴系只能设计成超静定结构，从而给其安装带来困难。此外，十字轴万向节的力学特性还产生周期性的轴向力，给本已十分复杂的轴承受力带来更不利影响。

总之，周期性的径向力和轴向力是十字轴万向节轴系所特有的，并会对这种轴系的设计、安装和维修产生不利影响。我们在设计、建造和维修时必须加以重视，确保轴承负荷在适宜的范围内。

［1］Voith Turbo.高性能万向轴产品 工程设计 服务［M］.Gemany：2016-03-10：38-39.

［2］刘鸿文.材料力学（Ⅰ）［M］.第4版.北京：高等教育出版社，2004：74-75.

［3］刘鸿文.材料力学（Ⅱ）［M］.第4版.北京：高等教育出版社，2004：88-94.

［4］艾维.船舶推进轴系十字轴万向节力学特性研究［D］.江苏科技大学，2007：17-18.

［5］宫国玺.船舶推进轴系校中计算研究［D］.大连理工大学，2007：9-10.

［6］孙培廷，李斌.船舶柴油机［M］.大连：大连海事大学出版社，2002：233-234.

［7］许宝森.船舶动力装置安装工艺［M］.北京：人民交通出版社，2010.

Force analysis of universal joint shaft of ship cross axle

CHEN Jun-yi ZHONG Wei-guo LUAN Jun
（Zhangjiagang Jiusheng Shipyard Co.，Ltd.，Zhangjiagang 215600，China）

The force situation of the shaft bearing installed in the ship cross axle universal joint is complex due to the influence of the cross axle universal joint.This paper briefly analyzes the mechanical properties and speed characteristics，as well as the force of the cross axle universal joint.On this basis，the radial load of each shaft bearing in the ship cross axle universal joint under various circumstances are calculated through the balance equation and three bending moment equations by using MATLAB and EXCEL.Finally，it briefly discusses the calculation method of the axial force on the cross axle universal joint，and the influence of the force on the shaft bearing，which can provide theoretical basis for the design，construction and maintenance of the shaft of the cross axle universal joint.

cross axle universal joint； balance equation； three bending moment equations； bearing； load

U664.2

A

1001-9855（2016）05-0069-09

2016-02-18；

2016-05-09

陈俊义（1979-），男，助理工程师，研究方向：船舶轮机建造安装工艺。仲伟国（1987-），男，助理工程师，研究方向：船舶轮机建造安装工艺。栾 军（1985-），男，助理工程师，研究方向：船舶轮机建造安装工艺。

10.19423/j.cnki.31-1561/u.2016.05.069