一种基于卡尔曼滤波的动态目标GPS定位算法

陈宝远　孙宇思　陈光毅　孙忠祥　吴丽华

摘要：针对动态目标的GPS定位精度不高和实时性较低的问题，通过改进卡尔曼滤波的定位算法，有效消除GPS动态数据的随机误差，给出了仿真得出的运动轨迹对比图和误差曲线对比图.该算法将速度观测量加入到常规的卡尔曼方程中，得出带约束项的改进型卡尔曼方程.通过实验结果可以看出该算法可以有效提高动态目标的GPs定位精度和实时性，具有重要的理论和实际意义.

关键词：动态目标；GPS定位；卡尔曼方程；约束项

Dol：10.15938/j.jhust.2016.04.00l

中图分类号：TN966

文献标志码：A

文章编号：1007—2683（2016）04—0001—06

0引言

全球定位系统（GPS）自1973年首次由美国国防部部署开始，凭借自身的高效益、高精度、自动化、全球性、全天候等显著特点，被广泛应用到大地测量、工程测量，水利、电力、交通、资源勘探和航海等领域中。

由于GPs的现代化进程飞速发展，其应用的范围越来越广泛，对其精度和速度也有了更高的要求.通过文献查阅可知，GPS动态定位一般可以分为伪距动态定位和载波相位动态定位.伪距定位平面坐标的精度可以最小可以达到0.48 m，载波相位定位平面坐标精度约为O.004m，但目前在GPS定位算法方面的研究还很不足，在滤波的过程中所用到的定位方程运算复杂，计算量很大，定位的精度低，速度慢，不适用于对动态目标的定位，本文对定位算法进行改进，通过分析GPS接收机的定位结果，设一个误差总和，其包含各种误差因素，由于定位的精度会受到速度观测量的影响，现将速度视为约束条件的卡尔曼方程与将速度视为观测量的常规卡尔曼方程联立.可以提高定位的精度和实时性，简化方程，减少计算量，对于GPS定位算法的发展而言，具有重要的理论和实际意义。

1.GPS定位误差分析

GPS为导航定位、测量和测量学开辟了一个崭新的时代.但由于GPS定位中含多种误差，利用传统的方法很难将其影响去除，使得GPS在某些场合的应用还受到限制，GPS定位的主要的误差源包括：①卫星测量误差.可分为：卫星时钟误差、星历误差、电离层的附加延迟误差、对流层的附加延时误差，②卫星的几何位置造成的定位误差，在运动目标定位中误差主要源于如下几种：多路径效应、信号遮挡、信号丢失、GPS接收机动态测量范围的局限性而引起的定位误差及首次定位的时延误差等。

影响GPS定位结果的误差因素也同时影响其测速情况，不过，接收机误差因素的影响表现显著，其他因素影响稍弱.接收机误差因素中接收设备的锁相跟踪环路掺人噪声，产生虚假的多普勒频移是其主要影响GPS测速的因素。

2.观测速度量的GPS定位算法

将误差因素均看成零均值的高斯白噪声，而实际情况中，很多信号显示为非白噪声分布.为了能提高GPS对于动态目标的定位精度和稳定性，对其信号的处理方式选用了卡尔曼滤波（kalman filter）算法.其原理是根据信号的前次估计值和当前观测值，通过利用线性无偏最小方差估计准则来推算得出当前的信号值，无需考虑以往观察值.还需已知状态方程、量测方程、白噪声激励的统计特性、量测误差的统计特性，其所用的信息均是属于时域内的.卡尔曼滤波适用于多维，其适用范围十分广泛，其特点有以下4种：

1）可以通过计算处理随机信号.

2）可以区分出所用被处理信号是否有用和干扰。

3）利用系统的白噪声激励和量测噪声的统计特性进行估算，不将其滤除。

4）算法属于递推类型，且在时域内使用状态空间法，适用多维随机过程。

卡尔曼滤波只利用信号的前次估计值和当前观测值，就可以对其进行线性无偏最小方差.

由于动态目标在运动过程具有复杂性，根据常规滤波方程处理可以发现其过程复杂、计算量大、实时性低等缺点.在实际使用的情况下，通过在GPS接收机上接收到的定位坐标进行预处理，并将所有的得到的误差加和计算.达到简化方程；减少数据处理量；减少得到的运算结果延迟性和准确性的目的。

2.2基于速度量的算法改进

2.2.1状态方程

在定位的实际应用中主要考虑平面的位置情

2.2.2改进后量测方程

比较GPS定位的速度数据和位置数据可得，其原理不相同，准确性则不同，速度数据的准确性高于位置数据的准确性，GPS定位过程中会输出的动态目标位置信息和速度信息，其中速度信息可分为速度的大小和方向，速度观测量影响GPS的定位精度，在观测方程中加入速度观测量可以提高定位精度，提高状态的可观测度。

将约束方程代人卡尔曼模型中，使得原本的卡尔曼方程的状态参数不满足新的条件方程。需要对其进行相应的修改，实现准确的滤波推导.根据采用最小方差估计原则，推导出新的带有速度约束条件的卡尔曼递推方程，并且保留原有发状态参数.

建立拉格朗日方程：解之得：最后得到带速度约束条件的卡尔曼算法递推公式：

它与常规的卡尔曼递推算法进行比较，改进后卡尔曼算法在预测值后加了一个和约束条件有关的修正项，没有对其他步骤进行改变.修正项是表示为最大化符合速度约束条件的要求，不间断的对载体运动的轨迹进行修正。

3.改进后算法仿真与对比

我们设定某一目标的起始位置在坐标轴的（0，0）上，本目标在x和Y轴上的初始加速度均为O.1m/s，设定本目标在坐标系内的运动为非规律运动，并且x和Y轴上分别给加速度增加了噪声影响，并且可以得到运动目标的运动轨迹.通过设定两部对目标进行实时测量的观察机以用来得知目标的相对距离.假设运动目标的状态向量、观测向量分别是：

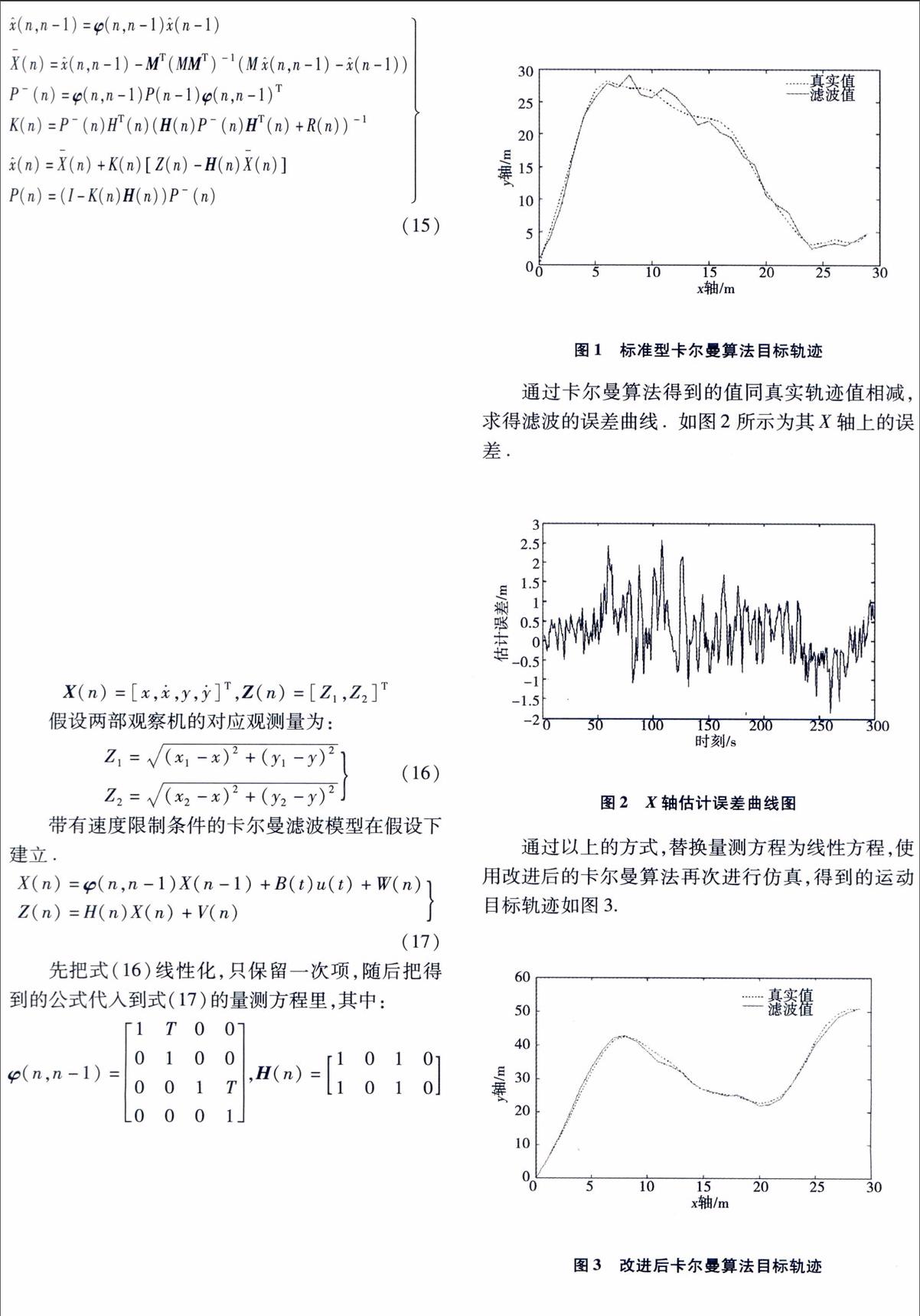
随后我们使用标准型卡尔曼方程对运动目标的轨迹进行滤波处理，其中它的系统噪声和量测噪声都是非相关独立高斯白噪声，其中设定时间T为1秒，在第3个历元介人滤波.全部过程耗费300秒，可以得到运动目标的轨迹如图1所示。

通过卡尔曼算法得到的值同真实轨迹值相减，求得滤波的误差曲线.如图2所示为其x轴上的误差。

通过以上的方式，替换量测方程为线性方程，使用改进后的卡尔曼算法再次进行仿真，得到的运动目标轨迹如图3.

通过图1和图3对比常规卡尔曼算法得到的轨迹和改进后卡尔曼算法得到的轨迹，可以看出后者更接近真实轨迹.通过图2和图4对比常规卡尔曼算法得到的误差曲线和改进后卡尔曼算法得到的误差曲线，可以看出后者误差明显减小.其原因是在相同条件下，改进后卡尔曼算法是将速度观测量代入状态变量中，并且作为速度约束条件代入卡尔曼方程，在系统方程不变的情况下，改进后的量测方程转换为：

而后利用Z₁和Z₂可以得到常规卡尔曼方程以及带约束项的卡尔曼方程，而后通过之前的运动轨迹模型在矩阵实验室中进行仿真，如图5和图6所示。

通过对比图可以直观得到带有速度约束项的改进后卡尔曼方程是很有效的降低了误差度.其误差值给出了比较有代表性的，如表1所示.

其原因为观测速度量的加入约束了状态量的变化，使物理意义与数学关系结合的更加直接，其改进后结果对预测值进一步进行了修正.这么做的优点是提高了坐标精度，得到的图像也证明了此点.综上所述：带有速度限制算法的卡尔曼量测方程能提高预测精度。

4.结论

传统卡尔曼滤波算法有着复杂程度高、数据处理量大、运算结果延迟较高等缺点.通过在GPs接收机上接收到的定位坐标进行预处理来克服以上缺点，预处理的算法是将速度观测量和普通卡尔曼观测方程统一计算，联立成一个带有速度限制做法的卡尔曼方程，并将所有的得到的误差加和计算.速度限制做法是在普通卡尔曼方程上建立的，未删除任何原始参数，最后进行MATAB仿真，通过实验结果可以分析出，本文所提出的改进后算法与常规算法相比，其稳定性和精确度都有一定程度的提高，本文在其他误差影响因素上未做深入研究，这一不足还需改进。