基于3σ准则的分段拟合及其GARCH修正模型
2016-11-09林静唐国强覃良文
林静+唐国强+覃良文


摘 要 在金融时间序列中,一组金融序列可被视为由不同时间段的分段函数拟合连接而成.利用3σ准则确定分段函数的临界点,并根据AIC准则及调整后R2对分段点进行验证,从而分段点把数据分割成两部分.对两序列分别用合适的函数进行拟合,并用ARMA-GARCH模型对残差序列进行修正.由上证综合指数数据的实证分析结果表明:3σ准则能很好地检索出临界点,同时建立的分段函数模型预测效果要优于ARMA与EGARCH模型,以及ARMA-GARCH模型的引入对模型的精确度有所提高.所介绍的方法简单易懂、便于操作、精度高,为金融投资者和学者提供参考价值.
关键词 应用统计数学;分段拟合;拉依达准则;GARCH模型;临界点
中图分类号 F224 文献标识码 A
Abstract In the financial time series, a group of financial sequence can be used as a function, in which piecewise fitting connection is made in different time periods. The Pauta criterion was exploited to determine the critical point of piecewise functions, according to AIC guidelines and coefficient of determination after adjustment to test breaking point, thus the staging point split the data into two parts. Two sequences were fitted with the appropriate function, and ARMA-GARCH model was used to amend the residual sequence. The empirical results of Shanghai composite index show that the 3 σ guidelines can retrieve critical point commendably. At the same time, the forecasting efficiency of piecewise function model is better than ARMA model and EGARCH model. Also, the precision of the model is improved by the introduction of ARMA-GARCH model. Moreover, the method is simple, easy to understand and operate, and accurate, which provides reference value for financial investors and scholars.
Key words Application of statistical; Sub-fitting; Pauta criterion; GARCH model; Critical point
1 引 言
从金融数据产生至今,对金融数据的分析一直是金融研究领域中一个倍受关注的焦点[1].运用科学的预测方法对金融序列进行预测具有十分重要的意义.从序列趋势波动的视角分析,序列的走势往往会呈现短期的上升或下降.在分析金融序列波动的趋势的基础上,提出了建立分段函数来对序列进行拟合.以分段函数的分段点作为突破点,在不同的时间区域中拟合合适的函数.
在分析较为复杂的数据时,往往采用分段曲线在区间内进行拟合逼近.赵丽坤和刘阳(2010)[2]指出分段函数是指自变量在不同范围取值时,有着不同的对应法则的一种函数,即用几个或无穷个解析式来近似表示曲线的函数.在实际生活中,很多问题都是多方面的,要考虑全面时常离不开分类讨论的思想,此时在解决日常生活中的问题(如,移动通话收费标准、个人应纳税所得税额、购物等)通常需要用到分段函数的模型函数.张兴元 (2007) [3]为了克服分段曲线拟合方法中存在不连续性与不可导性的缺陷,提出了一种分段函数的光滑算法,该方法在凸轮实验数据分段曲线拟合中得到了很好的拟合效果;刘丽坤和刘阳(2010) [4]采用系统工程的方法,并建立分段函数模型,和结合风险评价的复合方法对风险项目各阶段做出动态的决策.对于分段函数研究,很多学者是侧重于理论上对分段函数的求导与连续性来确定分段点的某个角度的定性认识,缺乏一定的说服力,而在文章中从定量的角度上确定分段点,引入拉依达准则进行确认分段点,使得分段函数模型更具有有效性与说服力.对于拉依达准则的研究,往往被应用于异常值的确定.陈俊等(2007) [5]在研究捕食模型的高精度参数估计中,针对时间变量出现的误差,采用了拉依达准则进行筛选,最终提出了一种较为简单的参数分段的动态估计算法.最近30年来,GARCH模型的应用在金融领域中发挥了较好的作用.刘青 (2015) [6]对上证综合指数收益率建立GARCH族模型进行比较,结果表明指数GARCH(EGARCH)模型可更好的预测资产收益率的波动过程.
借鉴以上研究中的一些基本成果,建立合理的预测模型,并与文献[6]推荐建立的EGARCH模型作对比,结果表明修正后的模型精度优于修正前的模型和EGARCH模型.文中的创新点在于运用拉依达准则确定分段函数的分段点和运用ARMA-GARCH模型修正残差序列.对分段点的确定实际上是逐步拟合合适的模型,找出异常的残差值.异常的残差对应的样本值是严重地偏离预测值,表明该样本点不宜于在该曲线上或者是不宜于用该曲线去拟合该样本点.异常值的判断,往往可以采用拉依达准则来确定.endprint
3 基于3σ准则的分段拟合
及模型修正的建模分析
3.1 数据的选取
在文章中,把上证综合指数作为研究对象进行说明文章的思想.上证综合指数是由上海证券交易所编制,用于体现上海证券市场层次丰富及行业拓展的市场结构和变化特征,同时是国际资本市场的一个重要参考数字[9].为了验证3σ准则用于分段拟合与ARMA-GARCH的修正模型的有效性,文中数据来源于同花顺金融网(数据来源路径:http://q.10jqka.com.cn/stock/zs/szzs/).利用收集到2014年6月3日到2016年4月30日的上证综合指数收盘价数据进行建模分析,总计469个数据(记为序列X,作为训练集,见图1所示).而2016年5月3日至2016年5月30日的上证综合指数数据为样本外检验数据,共20个数据.利用计量经济分析软件Eviews6.0和RStudio软件完成上证综合指数的建模过程.3.2 分段函数临界点的确定(3σ准则)
从图1中,可观察序列X前面一部分数据与后面一部分数据的波动情况不一致,总体上是先上升后下降,则采取分段函数的方法把数据分成两部分进行建模.但是,对于分段函数的临界点的确定成为了文章的关键.
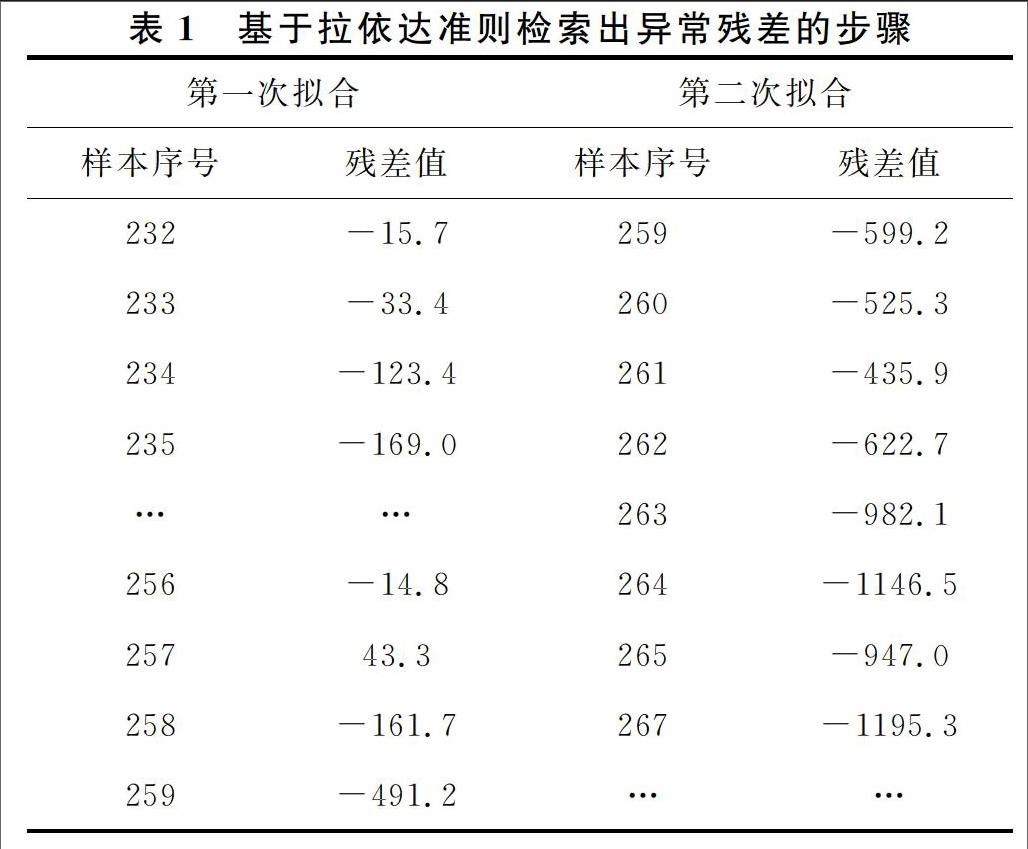
对前面50%数据(1-235)进行指数、二次函数、线性函数、对数函数、幂函数进行拟合,结果发现二次函数的拟合效果最好,求出预测值,并算出前面235个样本残差序列的3σ区间(-411.495,413.352),以及全部数据的残差.由表1可知,在第一拟合时,发现第259号残差的值不介于残差序列的3σ区间,则紧接着对前面258个样本重新拟合;从而得到前面258个样本残差序列的3σ区间为(-424.447,427.146),但是第259号残差值开始就不介于该区间内,则拟合结束,临界点为t=259.
方差方程中的ARCH和GARCH项的系数都是统计显著的,并且AIC和SIC值均变小,R方达到0.16.用以上ARMA(2,2)-GARCH(1,1)模型作残差序列的修正模型,拟合效果是比较理想的,走势基本一致,两曲线基本是重合的(见图2).因此引入ARMA-GARCH模型作修正模型能够更好的拟合数据,有助于提高模型的精度.
3.5 预测模型的有效性比较
综合式(3,4,5),可得出文章的最终模型,与对上证综合指数建立的ARMA模型做对比,并对样本外的数据进行预测,结果见下图3.
从图3可知,修正后的模型预测值以及走势最接近于上证综合指数收盘价实际值,而修正前的模型预测值和ARIMA(4,1,4)模型的预测值较为接近,EGARCH模型偏离实际值较大,均不如文中介绍的修正前与修正后的模型接近.经过计算2016年5月份20期四种模型的残余误差绝对值的和∑20i=1εi,其值依次分别为1 205.18,1 876.51,1 879.02,2 617.32.
由此可见,修正后模型的误差值最小,其次为修正前的模型,再者为ARIMA模型.在四种模型的比较中,修正后的模型对实际收盘价的预测性能要优于常规建立的ARIMA模型、EGARCH模型和修正前的模型;而修正前的分段函数模型的预测效果稍微比ARIMA模型要好,但是效果不是很明显.从方法的角度出发,引入ARMA-GARCH模型对分段函数模型残差做修正模型的预测效果有所提高;同时,用3σ准则确定临界点来建立的分段函数也可以提高模型的精度.四种模型所预测的二十期的预测值及其95%置信度区间如表6所示:
4 结 论
针对文章提出的模型修正以及样本区间确定的问题,采取了3σ准则确定样本区间的选择,并运用ARMA-GARCH模型对残差进行拟合,从而起到了模型修正的作用,有效地降低了误差值.根据上证综合指数的走势以及波动情况,从观察的视角出发,建立分段函数模型可能会比其他模型更有说服力.通过基于拉依达准则对上证综合指数建立分段函数,然后运用ARMA-GARCH模型对残差序列拟合,并与残差修正前模型、ARMA模型和EGARCH模型作对比,得出以下结论:
1)对于分段函数的分段点的确定是十分困难的,而文中提出引入3σ准则的方法恰好可以克服了这个问题,为文章后面分段拟合做铺垫,可以提高模型的精度,同时也为投资者提供了一种较为简单的分段函数方法.
2)分段函数的残差序列存在显著的ARCH效应,建立ARMA-GARCH模型可以提高模型的精度;从模型比较的角度出发,修正后的模型的拟合效果和预测效果均优于其他三种模型.通过修正前与修正后的模型对比,结果显示引入ARMA-GARCH模型对残差序列进行修正可以提高模型的精度,降低模型的误差,该修正方法可以给广大学者作参考.
参考文献
[1] 徐国祥.统计在金融领域的应用研究 [J].统计与决策,2012(2):33-36.
[2] 赵丽坤,刘阳.基于分段函数的风投项目复杂多阶段动态决策问题研究 [J].统计与决策,2010(20):42-44.
[3] 张兴元.分段函数的光滑方法及其在曲线拟合中的应用[J].西南民族大学学报,2007,33(3):486-490.
[4] 刘丽坤,刘阳.基于分段函数的风投资项目复杂多阶段动态决策问题研究[J].统计与决策,2010(20):42.
[5] 陈俊,乔海波,魏宏彬.捕食模型高精度参数的估计[J].数学的实践与认识,2007,37(14):67-73.
[6] 刘青,戴经跃,杨超.基于GARCH族模型的收益波动率预测绩效评估方法 [J].统计与决策,2015(9):160-163.
[7] 张敏,袁辉.拉依达准则与异常值剔除[J].郑州工业大学学报,1997,18(1):84-85.
[8] 李丽.基于ARMA-GARCH模型的股市量价动态关系研究 [J].统计与决策,2011(4):144-146.
[9] 于庆年.上证综合指数特征分析 [J].数理统计与管理,2012,31(2):374-375.endprint
