一种无拉伸畸变的动校正方法

孙成禹,谢俊法,2,闫月锋,林美言

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020)



一种无拉伸畸变的动校正方法

孙成禹1,谢俊法1,2,闫月锋1,林美言1

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.中国石油天然气股份有限公司勘探开发研究院西北分院,甘肃兰州730020)

动校正是地震数据处理的重要内容之一,采用常规动校正方法会产生拉伸畸变现象,在浅层和大炮检距处尤为明显,给地震资料的后续处理造成了不利影响。为此,分析了常规动校正方法产生拉伸畸变的原因,给出了动校正量可能的修正范围,提出了无拉伸畸变的动校正方法：①将近炮检距地震道进行常规动校正并叠加,得到标准道;②对地震道中每个时间样点的动校正量在给定的范围内进行修正扫描,并将常规动校正量加上修正量作为更新动校正量;③以待校正的时间样点为中心开时窗,使用更新动校正量进行动校正,并计算校正后时窗内数据与对应标准道数据的互相关系数;④将最大互相关系数对应的更新动校正量作为该样点的最终动校正量,以此实现无拉伸畸变动校正。模型数据测试和实际资料试处理结果显示了方法的正确性和有效性。

地震资料处理;动校正;拉伸畸变;互相关

在地震资料处理中,动校正的作用是消除炮检距对反射波传播时间的影响,将共中心点道集(CMP道集)中的反射波同相轴拉平,其精确性直接影响干扰波的压制效果以及后续偏移成像的质量。采用常规动校正方法存在同相轴无法拉平和拉伸畸变等问题,利用分偏移距动校正方法[1-2]或消除动校正剩余时差的方法[3-6]能够使同相轴拉平,但不能消除拉伸畸变。研究表明,动校正拉伸畸变通常发生在浅层和大炮检距处[7-11],具体表现为波形被拉长,频率被降低。常规地震数据处理中拉伸超过一定比例的数据被切除[10-11],这样浅层地震数据会因拉伸严重几乎全部或大部分被切除,导致覆盖次数降低。为了解决常规动校正的拉伸畸变问题,尽可能多地保留远道地震信息,施剑等[8]、LICHMAN[12]和崔宝文等[13]提出基于频谱替换的无拉伸动校正方法,使远道信息得到了保留。该方法理论上可以消除任何时差,并且由于采用快速傅里叶变换算法,具有很高的计算效率。但由于不同的同相轴在进行相位替换后会相互影响,因此实际数据处理中该方法常用于剩余时差校正[14]。RUPERT等[15]通过数据块整体移动并对重叠部分求和的方法进行动校正,在一个时窗内仅使用一个动校正量,避免了因动校正量不同而导致的拉伸畸变。但该方法在炮检距较大时容易出现同相轴的过校正和欠校正问题,在相邻时窗重叠处数据相加再除以叠加次数的方法也导致动校正效果变差。此外,该方法对弱反射层的动校正会受到相邻强反射层的影响。PERROUD等[16]、孟庆生[17]和HASSAN等[18]通过修改动校正速度使得同一个波形的各时间点具有相同的动校正量,从而消除了动校正拉伸畸变,但该方法需要找准每个同相轴的初至时间,实际资料由于波长从浅至深不断变化等因素,很难选取合适的时窗和时移因子。同时,速度修改后两个同相轴之间的速度变化加快,如果某个反射同相轴被遗漏,会比常规动校正更容易出现拉伸畸变。李录明[19]提出先自动检测反射波垂直反射时间和速度、后计算待校正炮检距的反射时间并将该时间处波形整体移动的方法,较好地消除了拉伸畸变,但该方法对速度分析的精度要求非常高。赵波等[20]采用动校正过程中的速度信息进行正演,再采用滤波方式消除动校正拉伸畸变,但该方法对速度分析的精度要求较高且计算量大。利用抛物Radon变换进行叠加的方法能够消除拉伸畸变[21-22],但必须在Radon域寻找一个合适的路径,或自动拾取能量团的聚焦点(存在噪声时可靠性较差),因此该方法在工业上的应用受到一定的限制。基于匹配追踪算法的无拉伸动校正方法[23]由于子波库的冗余性以及方法本身的问题会出现非正交投影和过匹配现象,计算效率和动校正效果会受到影响。BIONDI等[24]提出多次迭代的方法,每次迭代时进行部分动校正并利用反褶积来修正拉伸的影响,减小拉伸畸变,但每次迭代过程中采用的是常规动校正方法,动校正结果仍然会引入拉伸畸变。KAZEMI等[25]研究了局部无拉伸的动校正方法,将地震数据从浅到深划分多个时间窗口,重新计算出每个窗口内每个采样点的时距曲线后再进行动校正,但该方法要求多个反射波在零炮检距处不相互干涉,且大炮检距数据整体在时间方向上存在不连续的情况。

本文分析了常规动校正拉伸畸变的原因及动校拉伸的范围,给出一种无拉伸畸变的动校正方法,模型数据和实际资料处理测试证明了方法的可行性。

1　方法原理

1.1常规动校正拉伸分析

常规动校正方法中,地震反射波的时距方程为[7]：

(1)

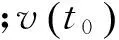
(2)

(3)

根据微分中值定理：

(4)

式中:t0ε为t01和t02之间的一点,

(5)

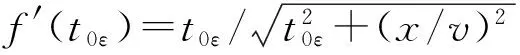
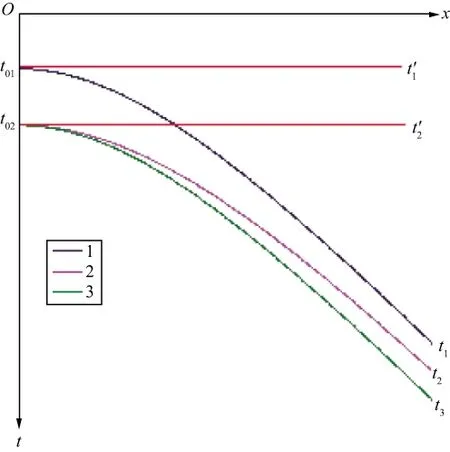
图1　常规动校正原理

1.2拉伸畸变的消除方法

由上述分析可见,产生动校正拉伸畸变的根本原因,是同一子波采用了不同的动校正量。子波内部不同样点间的动校正量变化越大,拉伸越严重。为有效压制这种拉伸畸变,我们对子波内各样点的动校正量进行动态调整,按照某种规则找出最佳动校正量。首先计算动校正量可能存在的修正范围,然后在修正范围内利用互相关算法筛选出无拉伸畸变的动校正量,最后使用该动校正量对道集数据进行“逐点搬家”,实现无拉伸畸变的动校正。

1.2.1动校正量的修正范围

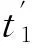
物理上子波的长度应保持不变,t02对应的时距曲线应该是在曲线1上加上t02-t01得到的结果,对应图1中的曲线3。所以曲线3的时距曲线方程是：

(6)

要使动校正后的子波不出现拉伸畸变,应计算波形初至时间的动校正量,且整个波形的校正都使用与之相同的动校正量。然而,实际动校正过程中每一个波形的初至时间很难获取,其速度也不是固定不变,而是随时间变化的函数,因而t3也不容易求取。

可以认为,曲线3是曲线2加一个修正量得到的结果,当t02=t01时,修正量为0;当t01和t02恰好在波形两端,即子波长度λ=t02-t01时,修正量最大。考虑到速度随时间变化,炮检距为x时t0时间的动校正量最大修正范围是：

(7)

其中,

(8)

1.2.2修正量的筛选

在动校正量的修正范围内,存在一个最佳修正量,用它对常规动校正量进行修正,能够有效消除拉伸畸变。从动校正量的修正范围内筛选最佳修正量的步骤如下。

1) 建立标准道。为减小动校正拉伸畸变对标准道的影响,可采用常规动校正后近道数据的叠加作为标准道[5]。

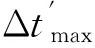
3) 选取数据时窗。对于标准道,以t0为中心选取一定长度的数据时窗；对于待校正道,由于同一个波形应具有相同的动校正量,故以t为中心确定与标准道相同长度的数据时窗。因为不同波形的动校正量不同,所以数据时窗的长度不宜太长。

4) 计算互相关量。对待校正道时窗内数据和标准道时窗内数据进行归一化互相关计算,将互相关值作为评价动校正效果的准则。归一化互相关公式如下：

(9)

式中:rcor表示互相关系数;N为时窗长度;w(tj)为待校正道时窗内的数据;m(tj)表示标准道时窗内的数据。

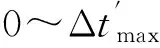
重复步骤2)至步骤4),确定所有t0时间和所有道的动校正量,即可依次完成动校正。

1.2.3无拉伸畸变的动校正

相邻同相轴之间可能存在无波形信息的空白区域,该区域的大小随炮检距的不同而变化,常规动校正对同相轴和同相轴之间的空白区域都存在拉伸。无拉伸畸变的动校正通过对动校正量进行修正,使得同一反射波组的波形不被拉伸,但由于同一反射波组的t0时间唯一,波组之间的空白区域势必会被拉伸。因此,无拉伸畸变的动校正相当于把常规动校正对反射波组的拉伸进行修正,并把拉伸量转嫁给了空白区域。

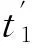
2　模型数据测试

2.1无同相轴交叉的模型

建立5层介质模型一,各层速度分别为2000,2100,3000,3500和3700m/s,反射层深度分别为300,700,1200,1800m。通过正演获得图2a所示的模型一数据,共180道,道间距是10m,最小炮检距为0,模型中4个同相轴不出现交叉。图2b 是对模型一数据进行常规动校正的结果,可以看出同相轴①和②在大炮检距处出现了拉伸畸变,没有被拉平,其余两个同相轴的拉伸较小,基本看不出畸变,说明常规动校正方法容易在浅层和远道处出现拉伸畸变。图2c是模型一数据采用本文方法的动校正结果,可以看出4个同相轴均已拉平且没有出现畸变,说明本文方法是有效可行的。图2d 是两种方法动校正结果的叠加波形对比,为清楚地展示动校正效果,本文仅截取了0.25～0.45s之间同相轴①的数据进行显示。从图2d可以看出,常规动校正结果由于远道处出现拉伸,叠加波形的振幅偏小,且波形被拉伸;本文动校正方法由于使同相轴得到拉平,实现了各道数据的同相叠加,因此叠加后波形特征得到了保持,振幅比常规动校正方法大。波形的拉伸会造成频率的降低,且随着炮检距的增大,常规动校正的拉伸会越来越严重,主频向低频方向的移动也越来越多。图2e是对常规动校正结果(图2b)逐道进行傅里叶分析得到的振幅谱,从第80道开始明显出现频率范围向低频方向移动的现象,这与图2b中子波的拉伸现象一致,图2e中的频率向低频方向的移动越明显,图2b中地震道的拉伸畸变越严重。图2f是对本文方法动校正结果(图2c)逐道进行傅里叶分析得到的振幅谱,可以看出,各道地震数据的主频基本一致,没有出现频带移动的现象。

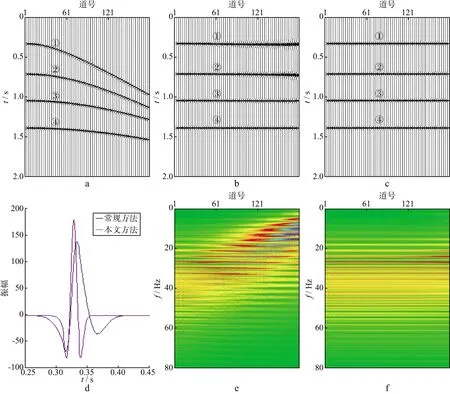
图2　无同相轴交叉的动校正a 无同相轴交叉的模型; b 常规动校正结果; c 本文方法动校正结果; d 叠加结果对比; e 常规动校正结果的振幅谱; f 本文方法动校正结果的振幅谱

2.2存在同相轴交叉的模型

在地层倾斜等复杂构造条件下,有可能出现深层界面的反射波旅行时小于浅层的情形,即出现同相轴交叉的现象。在地层厚度很小时,反射波同相轴也可能存在一定的干涉。不失一般性,我们构造图3a 所示的模型二数据,分析存在同相轴交叉及干涉情形的动校正拉伸。该模型数据共180道,最小炮检距为0,道间距为10m,同相轴①和同相轴②在140道附近的A点交叉,同相轴③和同相轴④存在干涉。图3b是模型二数据常规动校正结果,由于常规动校正根据速度计算动校正量,在同相轴交叉后,同相轴②出现的时间比同相轴①出现的时间早,导致同相轴①上方出现同相轴②的信息[23-24]。由于速度逐渐增大,同相轴①在交叉点附近难以显示整个波形,出现被“劈开”的现象,在同相轴②下方会出现同相轴①的信息;同相轴②在与同相轴①发生交叉之后的部分会出现两次过校正,且这两次过校正在A点相交。因为常规动校正在“搬家”完成后并不抹去原先的信息,所以同相轴①和同相轴②可能出现多次。图3c是模型二数据使用本文方法动校正的结果,图中两个同相轴均已拉平,虽然在交叉点A附近的校正效果与其它区域相比要略差一点,但依然没有出现拉伸畸变。与常规动校正方法不同,由于本文方法只选择互相关值大于0时对应的动校正量,因此同相轴①的信息不会在不同区域多次出现。图3d是常规方法和本文方法动校正结果的叠加波形对比,为清楚地展示动校正效果,本文仅截取0.80～0.88s之间同相轴①的数据进行显示。由图3d可见,常规动校正结果被同相轴②的信息所干扰,叠加后波形发生畸变;本文方法由于使同相轴得到了拉平且不受同相轴②的干扰,各道数据实现了同相叠加,叠加后波形特征得到保持,叠加后振幅比常规动校正结果强。图3e是对常规动校正结果(图3b)逐道进行傅里叶分析得到的振幅谱,由于同相轴①在不同区域出现两次,同相轴②在不同区域出现3次,导致各道振幅谱之间变化较大,且在交叉点A处有一条贯穿低频到高频的线,在50道之后出现频率范围明显向低频方向移动的现象。图3f是对本文方法动校正结果(图3c)逐道进行傅里叶分析得到的振幅谱,可以看出,各道数据没有发生频率范围移动的现象,虽然在交叉点A附近依然存在频率范围贯穿低频到高频的线,但已经得到了很大改善。这条线是由于两个交叉同相轴的波形未能完全分离导致的。

为分析反射波同相轴存在干涉时的动校正效果,对同相轴③和④的分炮检距叠加波形进行放大显示。图4a为常规动校正方法和本文动校正方法在0～500m炮检距范围的叠加结果对比,可见两种方法的叠加波形几乎完全一致,说明常规方法在近炮检距的拉伸量很小。为了分析两种方法对远炮检距数据的动校正效果,对常规方法动校正后不同炮检距的叠加波形进行放大显示,如图4b所示,

可见炮检距越大,波形拉伸越严重。图4c是本文方法动校正后不同炮检距的叠加波形对比,可见各炮检距的波形都未出现拉伸,但由于大炮检距比近炮检距的波形干涉严重,因此,随着炮检距增大,叠加波形的振幅略微减小。

2.3抗噪性分析

为了测试本文方法对随机噪声的敏感性,在图2a 所示的模型数据中加入随机噪声,使其信噪比分别为5∶1,1∶1和0.5∶1.0,进而分析本文方法对高信噪比、中等信噪比和低信噪比数据的处理效果(图5)。

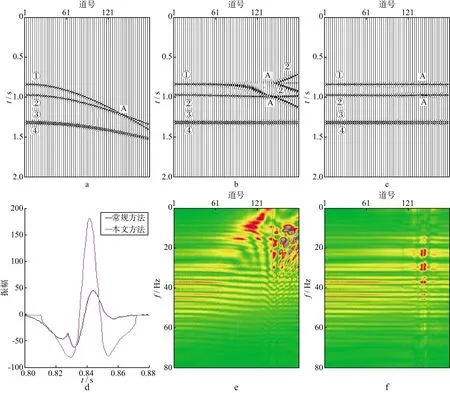
图3　交叉同相轴的动校正a 存在同相轴交叉的模型; b 常规动校正结果; c 本文方法动校正结果; d 叠加结果对比; e 常规动校正结果的振幅谱; f 本文方法动校正结果的振幅谱

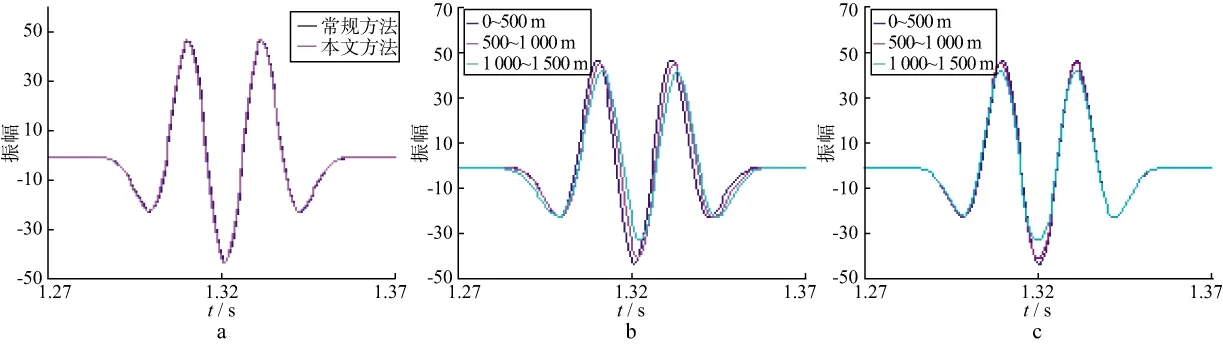
图4　干涉同相轴的校正结果分析a 两种方法在0～500m炮检距范围的叠加波形对比; b 常规方法不同炮检距的叠加波形对比; c 本文方法不同炮检距的叠加波形对比

图5a,图5d,图5g分别是信噪比为5∶1,1∶1和0.5∶1.0的模型数据,随着信噪比的降低,同相轴逐渐被淹没在噪声中。图5b,图5e,图5h是对应的常规动校正结果,同相轴的拉伸畸变几乎不随信噪比的降低而变化。图5c,图5f,图5i是本文方法的动校正结果,对于不同信噪比数据,同相轴都能够被拉平且无畸变。图6对比了图5中动校正结果的叠加波形(为了清楚地展示出动校正效果,仅显示了第一个同相轴),可见常规动校正方法由于在大炮检距处存在拉伸畸变,导致非同相叠加,因此叠加波形的振幅小于本文方法,且波形被拉伸,拉伸程度不随信噪比的降低而改变,说明常规动校正拉伸畸变对信噪比变化不敏感。本文动校正方法则由于控制了拉伸畸变,叠加波形未被拉伸,然而在同相轴以外的区域,噪声能量随着信噪比的降低而增强,这是由于选择动校正量时,与标准道波形相似的噪声被作为有效波进行了处理,导致相干噪声被增强。因此,使用本文方法处理低信噪比数据时,需先进行叠前去噪。

图5　不同信噪比数据动校正效果分析a,d,g 信噪比为5∶1,1∶1,0.5∶1.0的模型数据; b,e,h 常规方法对图5a,图5d,图5g的动校正结果; c,f,i 本文方法对图5a,图5d,图5g的动校正结果

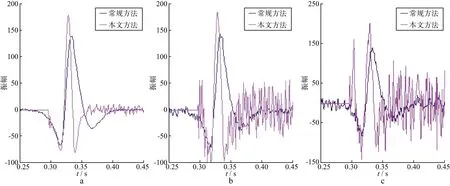
图6　不同信噪比数据动校正后叠加结果对比a 信噪比为5∶1; b 信噪比为1∶1; c 信噪比为0.5∶1.0

3　实际地震数据试处理

采用我国东部某地区道间距为50m,信噪比

较高的地震数据对本文方法的有效性与实用性进行了测试(图7)。图7a为实际CMP道集,图7b是常规动校正结果(仅截取0～1.2s之间的数据进行了显示)。可以看出,经过常规动校正后同相轴基本被校平,但大炮检距的同相轴比近炮检距的同相轴要宽,说明波形被拉伸。图7c为采用本文方法动校正的结果,同相轴均已拉平且未出现拉伸现象。图7d是两种方法动校正结果的叠加数据对比(为清楚地展示动校正效果,只显示了0.9～1.2s之间的数据),可以看出,由于本文方法动校正的波形没有被拉伸,叠加后波形的振幅大于常规方法。图7e 是对常规方法动校正结果(图7b)逐道进行傅里叶分析得到的振幅谱,可以看到前20道数据的频率范围基本没变,但20道之后的频率逐渐向低频方向移动,这是由波形拉伸所致。图7f是对本文方法动校正结果(图7c)逐道进行傅里叶分析得到的振幅谱,由于波形没有被拉伸,各道数据的频率范围基本不变,说明本文方法能够对实际资料有效进行无拉伸畸变的动校正。

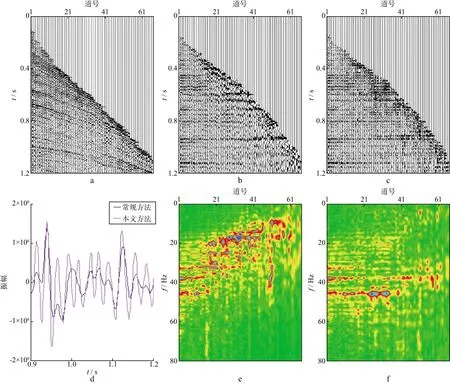
图7　实际地震数据动校正效果分析a 实际CMP道集; b 常规动校正结果; c 本文方法动校正结果; d 两种方法叠加结果对比; e 常规动校正结果的振幅谱; f 本文方法动校正结果的振幅谱

图8比较了实际叠加剖面,道间距为25m。图8a为常规动校正后的叠加剖面,由于存在拉伸畸变,导致非同相叠加,因此部分同相轴连续性较差。图8c为本文方法动校正后的叠加剖面,由于动校正过程中同相轴均已拉平且不出现拉伸,叠加后的波形能量得到加强,图8a中部分能量较弱的同相轴也被加强,连续性得到较大的改善,剖面整体的分辨率得到提高。图8b和图8d分别是图8a和图8c各道地震数据的振幅谱,常规方法的主频在20Hz附近,而本文方法的主频约为35Hz,比常规方法提高了15Hz。

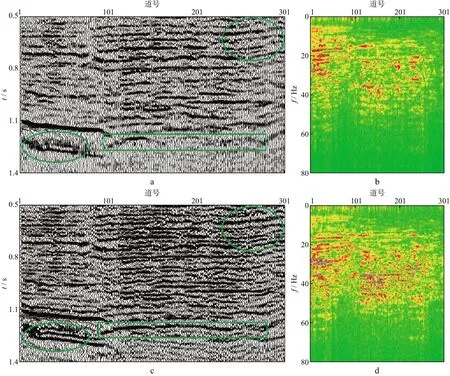
图8　实际叠加剖面对比a 常规动校正叠加剖面; b 常规动校正结果的振幅谱; c 本文方法动校正叠加剖面; d 本文方法动校正结果的振幅谱

4　结论

本文分析了地震资料处理中常规动校正产生拉伸畸变的原因,研究了修改动校正量以减少拉伸畸变的方法,模型数据测试和实际资料处理验证了方法的正确性与有效性,得出如下结论：

1) 将常规动校正后近炮检距的叠加道作为标准道,计算与标准道的互相关,在一定范围内对常规动校正量进行修正,可以消除拉伸畸变。

2) 对于含有一定噪声的数据,本文方法仍然可以实现无拉伸畸变的动校正,但随着信噪比的降低,叠加波形中同相轴之外的相干噪声能量增强,因此,将本文方法应用于低信噪比数据时,需先进行叠前去噪处理。

致谢:本文研究过程中,中国石油大学(华东)地球科学与技术学院伍敦仕博士与中国石油化工股份有限公司胜利油田分公司物探研究院赵爱国博士参与了讨论并给予了宝贵的帮助,在此表示感谢。

[1]王鑫,陈新荣.分偏移距动校正技术[J].石油物探,2003,42(2):212-214

WANG X,CHEN X R.Offset division normal moveout correction[J].Geophysical Prospecting for Petroleum,2003,42(2):212-214

[2]陈雨红,李强.分偏移距动校正方法的改进[J].石油物探,2007,46(2):107-111

CHEN Y H,LI Q.Improvement of offset division NMO[J].Geophysical Prospecting for Petroleum,2007,46(2):107-111

[3]马永军,王季.一种改进的时间域剩余动校正方法[J].石油物探,2010,49(3):245-247

MA Y J,WANG J.An improved residual normal moveout correction method in time domain[J].Geophysical Prospecting for Petroleum,2010,49(3):245-247

[4]苑春方,语钦范,王彦纯,等.动校正剩余时差的估计与校正[J].石油物探,2002,41(3):317-320

YUAN C F,YU Q F,WANG Y C,et al.Estimation and removal of residual normal moveout[J].Geophysical Prospecting for Petroleum,2002,41(3):317-320

[5]慎国强,王玉梅,孟宪军,等.基于时频分析的地震道校平技术应用[J].中国石油大学学报(自然科学版),2010,34(1):34-36,45

SHEN G Q,WANG Y M,MENG X J,et al.Application of seismic gather flattening technique based on time-frequency analysis[J].Journal of China University of Petroleum,2010,34(1):34-36,45

[6]张汛汛,张繁昌,刘汉卿.基于快速匹配追踪算法的地震道集剩余时差校正[J].石油物探,2015,54(4):420-426

ZHANG X X,ZHANG F C,LIU H Q.Seismic gathers residual moveout correction based on fast matching pursuit algorithm[J].Geophysical Prospecting for Petroleum,2015,54(4):420-426

[7]李秉富,魏长江.地震资料动校正拉伸畸变分析[J].青岛海洋大学学报,1994,24(S3):39-44

LI B F,WEI C J.The analysis of anomalous stretch of normal moveout in seismic data processing[J].Journal of Ocean University of Qingdao,1994,24(S3):39-44

[8]施剑,吴志强,刘江平,等.动校正拉伸分析及处理方法[J].海洋地质与第四纪地质,2011,31(4):187-194

SHI J,WU Z Q,LIU J P,et al.Normal moveout stretch correction and its processing method[J].Marine Geology & Quaternary Geology,2011,31(4):187-194

[9]DUNKIN J W,LEVIN F K.Effect of normal moveout on a seismic pulse[J].Geophysics,1973,38(4):635-642

[10]BUCHHOLTZ H.A note on signal distortion due to dynamic (NMO) corrections[J].Geophysical Prospecting,1972,20(2):395-402

[11]李振春,张军华.地震数据处理方法[M].东营：中国石油大学出版社,2004:118-131

LI Z C,ZHANG J H.Seismic data processing method[M].Dongying:China University of Petroleum Press,2004:118-131

[12]LICHMAN E.Automated phased-based moveout correction[J].Expanded Abstracts of 69thAnnual Internat SEG Mtg,1999:1150-1153

[13]崔宝文,王维红.频谱代换无拉伸动校正方法研究[J].地球物理学进展,2007,22(3):960-965

CUI B W,WANG W H.Spectral borrowing stretch-free normal moveout correction[J].Progress in Geophysics,2007,22(3):960-965

[14]林伯香,孙建国.相位替换法剩余时差校正[J].石油物探,2001,40(3):15-22

LIN B X,SUN J G.Residual moveout correction by using phase replacement[J].Geophysical Prospecting for Petroleum,2001,40(3):15-22

[15]RUPERT G B,CHUN J H.The block move sum normal moveout correction[J].Geophysics,1975,40(1):17-24

[16]PERROUD H,TYGEL M.Nonstretch NMO[J].Geophysics,2004,69(2):599-607

[17]孟庆生,樊玉清,郭秀军,等.无拉伸动校正技术在近海工程地震勘探中的应用[J].地球物理学进展,2007,22(6)：1889-1894

MENG Q S,FAN Y Q,GUO X J,et al.The application of non-stretch NMO on offshore engineering seismic exploration[J].Progress in Geophysics,2007,22(6):1889-1894

[18]HASSAN M H,BARTON P J,SINGH S C.Nonstretch moveout correction of long-offset multichannel seismic data for subbasalt imaging:example from the North Atlantic[J].Geophysics,2010,75(4):R83-R91

[19]李录明.浅层地震资料无畸变动校正[J].石油物探,1991,30(4):81-88

LI L M.Undistorted dynamic correction for seismic data from shallow reflectors[J].Geophysical Prospecting for Petroleum,1991,30(4):81-88[20]赵波,史政军.消除动校正拉伸影响的方法[J].石油地球物理勘探,1995,30(3):417-421

ZHAO B,SHI Z J.A method for removing NMO correction lengthening[J].Oil Geophysical Prospecting,1995,30(3):417-421

[21]KABIR M M N,VERSCHUUR D J.Integrated velocity estimation and stacking using parabolic Radon transform[J].Expanded Abstracts of 64thAnnual Internat SEG Mtg,1994:1473-1476

[22]HICKS G J.Removing NMO stretch using the Radon and Fourier-Radon transforms[J].Expanded Abstracts of 63rdEAGE Annual Conference,2001:A18

[23]ZHANG B,ZHANG K,GUO S,et al.Nonstretching NMO correction of prestack time-migrated gathers using a matching-pursuit algorithm[J].Geophysics,2013,78(1):U9-U18

[24]BIONDI E,STUCCHI E,MAZZOTTI A.Nonstretch normal moveout through iterative partial correction and deconvolution[J].Geophysics,2014,79(4):V131-V141

[25]KAZEMI N,SIAHKOOHI H R.Local stretch zeroing NMO correction[J].Geophysical Journal International,2012,188(1):123-130

(编辑：戴春秋)

A NMO correction method without stretching distortion

SUN Chengyu1,XIE Junfa1,2,YAN Yuefeng1,LIN Meiyan1

(1.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China; 2.NorthwestBranchInstitute,ResearchInstituteofPetroleumExplorationandDevelopment,CNPC,Lanzhou730020,China)

Normal moveout (NMO) correction is one of the important procedures in seismic data processing.The conventional NMO correction method usually causes stretching distortion,especially in shallow layer and at large offset,which will adversely affect the subsequent processing of seismic data.Therefore,we analyzed the reasons for generating stretching distortion by conventional NMO correction and calculated the possible revising range of NMO correction values,and then a NMO correction method without stretching distortion was proposed.Firstly,we stack the near-offset traces after conventional NMO correction and take the stacking trace as standard trace.For every time sampling data,we estimate the updated NMO correction values by giving different disturbances which are selected within the revising range and added to the conventional NMO correction values.Moreover,we select a time window centering on this sampling data and carry out NMO correction using every updated NMO correction value,then calculate the cross-correlation coefficient of the corrected data in this window and corresponding standard trace.Finally,the best NMO correction value is defined as the value corresponding to the largest cross-correlation coefficient,to realize NMO correction without stretching distortion.The accuracy and effectiveness of this method are proved by model and practical data processing.

seismic data processing,NMO correction,NMO stretching distortion,cross-correlation

2015-09-29;改回日期：2015-12-30。

孙成禹(1968—),男,教授,博士生导师,主要从事地震波传播理论与地震勘探方法的教学和研究工作。

国家自然科学基金(41374123)和中国石油化工股份有限公司地球物理重点实验室开放研究基金(33550006-14-FW2099-0035)联合资助。

P631

A

1000-1441(2016)05-0664-10

10.3969/j.issn.1000-1441.2016.05.005

This research is financially supported by the National Natural Science Foundation of China (Grant No.41374123) and SINOPEC Key Laboratory of Geophysics Open Foundation (Grant No.33550006-14-FW2099-0035).