使用GPU加速计算矩阵的Cholesky分解
2016-11-09高火涛
沈 聪 高火涛
(武汉大学电子信息学院 湖北 武汉 430072)
使用GPU加速计算矩阵的Cholesky分解
沈聪高火涛
(武汉大学电子信息学院湖北 武汉 430072)
针对大型实对称正定矩阵的Cholesky分解问题,给出其在图形处理器(GPU)上的具体实现。详细分析了Volkov计算Cholesky分解的混合并行算法,并在此基础上依据自身计算机的CPU以及GPU的计算性能,给出一种更为合理的三阶段混合调度方案,进一步减少CPU的空闲时间以及避免GPU空闲情况的出现。数值实验表明,当矩阵阶数超过7000时,新的混合调度算法相比标准的MKL算法获得了超过5倍的加速比,同时对比原Volkov混合算法获得了显著的性能提升。
图形处理器乔里斯基分解加速比混合算法
0 引 言
近年来,随着计算机技术的发展,图形处理器(GPU)越来越强大,并且在计算能力上已经超过了通用CPU。使用GPU计算可以以低廉的价格获得巨大的计算性能,因此成为了科学计算领域的一个应用热点。自2007年NVIDIA公司推出了CUDA运算平台,并使用C语言为CUDA构架编写程序以来,GPU计算技术已经广泛应用于诸如信号处理、图像处理、信息安全等热门领域中。在数值线性代数中,GPU可以用于加速大规模的矩阵计算问题,包括矩阵的分解和求特征值以及特征向量等。许多组织和机构在GPU上实现了LAPACK库中的函数,并发布了相关软件包以供科研人员使用。比较著名的软件包有CULA和MAGMA等。
Cholesky分解是矩阵计算中的一个基本分解问题,常常用于求解系数矩阵为对称正定矩阵的线性方程组,由于其计算量比使用LU分解求解一般线性方程组的算法约减少一半。因此在科学计算中也有广泛的应用。此外,Cholesky分解也应用于Kalman 滤波[1]以及Monte Carlo仿真[2]等算法中。随着基本矩阵算法在科学计算中广泛使用以及其处理的数据矩阵越来越大,研究使用GPU加速矩阵计算问题是十分必要的。
CUBLAS是在GPU上实现的BLAS。利用CUBLAS库可以很方便地移植CPU代码到GPU上进行加速计算。自2008年Volkov等人提出CPU-GPU混合计算矩阵的LU、Cholesky和QR分解算法[5]以来,混合算法思想被广泛应用于各个计算领域,如流体仿真计算[6]、光线跟踪算法[7]等。混合算法思想也因为Volkov等人的工作正逐步应用于各基本矩阵算法中,如矩阵的Hessenberg约化、二对角化以及矩阵的特征值求解中。使用CPU-GPU混合算法可以通过减少CPU的空闲时间,进一步加速矩阵计算。然而混合算法的性能很大程度上取决于调度算法的优劣。好的调度方案可以最小化CPU与GPU的空闲时间,达到混合最优的目的;不适当的调度策略可能导致计算错误或者计算时间的延长。基于此,本文将在最新的Kerpler GPU构架上重新考察Volkov的混合算法,并给出一种新的调度方案,以达到混合更优的目的。数值实验表明基于新的三阶段混合调度算法的函数New_Sche相比MKL中的dpotrf函数最高获得了5.2倍的加速比,而且其计算性能显著优于原Volkovde 混合算法。文中给出的针对Cholesky分解的调度策略同样适用于矩阵的其他分解及约化算法。
1 使用CPU计算Cholesky分解
给定一个对称正定矩阵A,则存在主对角元素全为正数的下三角矩阵L满足:
A=LLT
(1)
通常称下三角矩阵L为矩阵A的Cholesky因子。下面给出Cholesky分解的直接算法[3]及基于块的下递推更新算法[4]。
1.1直接Cholesky分解
对于对称正定矩阵A直接由式(1)得到如下等式:
(2)
则对于第j个对角元素ajj,有:
(3)
对于位置为(i,j)(i>j)的元素,我们可得如下等式:
aij=ri1rj1+ri2rj2+…+rijrjj
(4)
由此可得到求解Cholesky分解的公式如下:
(5)
(6)
若令j=1,2,…,n,循环使用式(5)、式(6)计算L的下三角元素,这样便得到计算Cholesky分解的直接算法。由于该直接算法主要是Level 2 BLAS操作,不适合移植到GPU上计算。
1.2基于块的Cholesky分解
BLAS库内部实现了各种线性代数的基本运算。由于其代码的高效性和完整性,因此一直为科研人员广泛使用。其中Level3BLAS是依据现代计算机的内存等级进行了大量的优化处理,使得其计算性能远高于Level2BLAS。类似的结论也在GPU上成立。
为了能利用矩阵的子块进行计算,下面使用Cholesky分解的块递推更新算法。对矩阵A进行分块,如下:

A=A11BTBA^[] A11∈

则由式(1)有:

A=A11BTBA^[]=L110SL^[]LT11ST0L^T[]
于是得到如下递推公式:
L11=cholesky(A11)
(7)
(8)
(9)
对矩阵按式(7)-式(9)依次递推更新下去,便可得到Cholesky分解。
具体的递推过程如图1所示。

图1 基于块的Cholesky分解
1.3算法及分析
基于块的Cholesky分解算法如下:
Step1使用IntelMKL库中的dpotrf函数计算第一个子块A1的Cholesky分解;
Step2使用BLAS库中的Level3函数trsm求解矩阵方程X×A1T=A2;
Step3使用BLAS库中的Level3函数syrk更新尾部矩阵A3=A3-A2×A2T;
Step4对尾部矩阵A3重新分块并针对A3重复执行以上三步,直到计算完最后一个子块的Cholesky分解则结束。
在余部矩阵A3的阶数较大时,Step3占据一次循环约80%的计算时间。而A1由于分块大小的固定,计算量不会改变,Step1所占的计算时间非常小。当A2的行远大于分块值时,Step2几乎占据了剩余20%的计算时间。
2 使用GPU计算Cholesky分解
2.1CUBLAS库
CUBLAS是由NVIDIA公司提供的并在CUDA构架的GPU上实现BLAS的函数库。利用CUBLAS库可以很方便地移植矩阵计算的CPU代码到GPU上进行计算。由于矩阵算法中主要涉及矩阵与矩阵相乘等的Level 3操作以及矩阵和向量相乘等的Level 2操作,且BLAS和CUBLAS库中的函数是经过高度优化的,并被全世界广泛认可,因此在计算Cholesky分解中,可直接使用该库中的函数在CPU或GPU上实现矩阵的Level 2或Level 3操作。这样,可以将主要精力放在Cholesky分解算法的任务划分及任务调度上。
2.2使用CUBLAS计算Cholesky分解
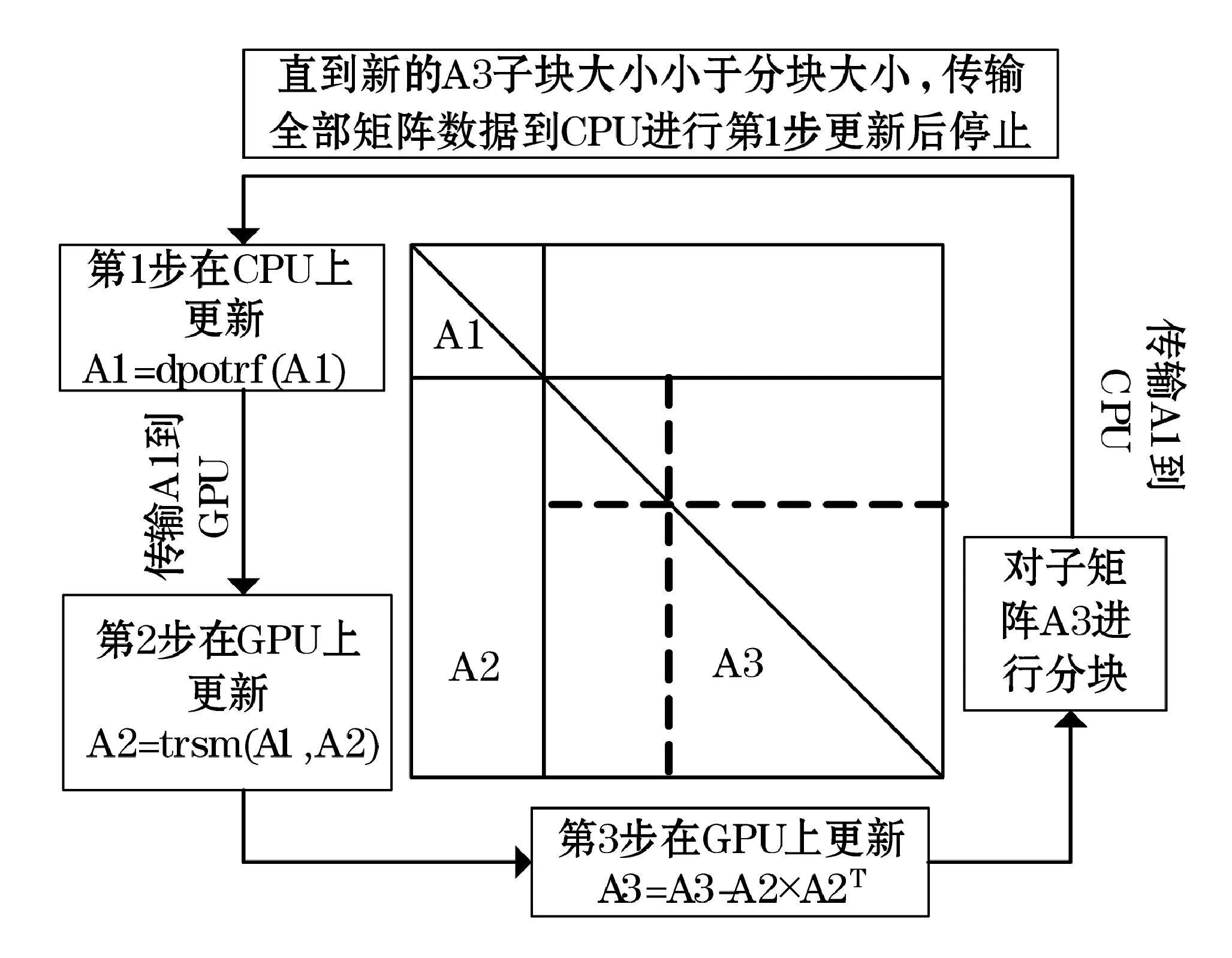
图2 使用CUBLAS加速Cholesky分解
由于CUBLAS库中提供了trsm和syrk函数,但没有提供potrf函数。对此,可以在每次循环时先将需要计算Cholesky分解的子矩阵块传回到CPU上并利用MKL中的potrf函数计算其Cholesky分解,然后在将结果传输至GPU对应的位置。再依次使用CUBLAS库函数在GPU上更新矩阵的剩余部分。然而这样做的结果是当GPU(或CPU)执行计算任务时,CPU(或GPU)处于闲置状态,这导致了硬件资源的浪费。使用CUBLAS计算Cholesky分解的具体过程如图2所示。
这样直接使用CUBLAS库函数加速实对称正定矩阵的Cholesky分解的效果也是十分明显的。首先由于在GPU上的操作全为Level 3的BLAS操作;其次,相对较小的分块值nb,如nb<512,在本实验环境下,使用MKL库函数计算512阶对称正定矩阵的Cholesky分解耗时约为4 ms,而来回传输512阶矩阵总共耗时约2 ms。相比较大的对称正定矩阵而言,直接使用CUBLAS库函数已经可以称之为充分利用GPU进行计算了。
2.3Volkov的混合算法及分析
Volkov等人于2008年给出了CPU-GPU混合计算Cholesky分解的算法[5],并在NVIDIA的GTX 280上获得了良好的加速效果。该算法随后被MAGMA软件包采纳,成为计算Cholesky分解的标准算法之一。图3-图6以4×4的矩阵块为例,简单描述Volkov的混合算法。
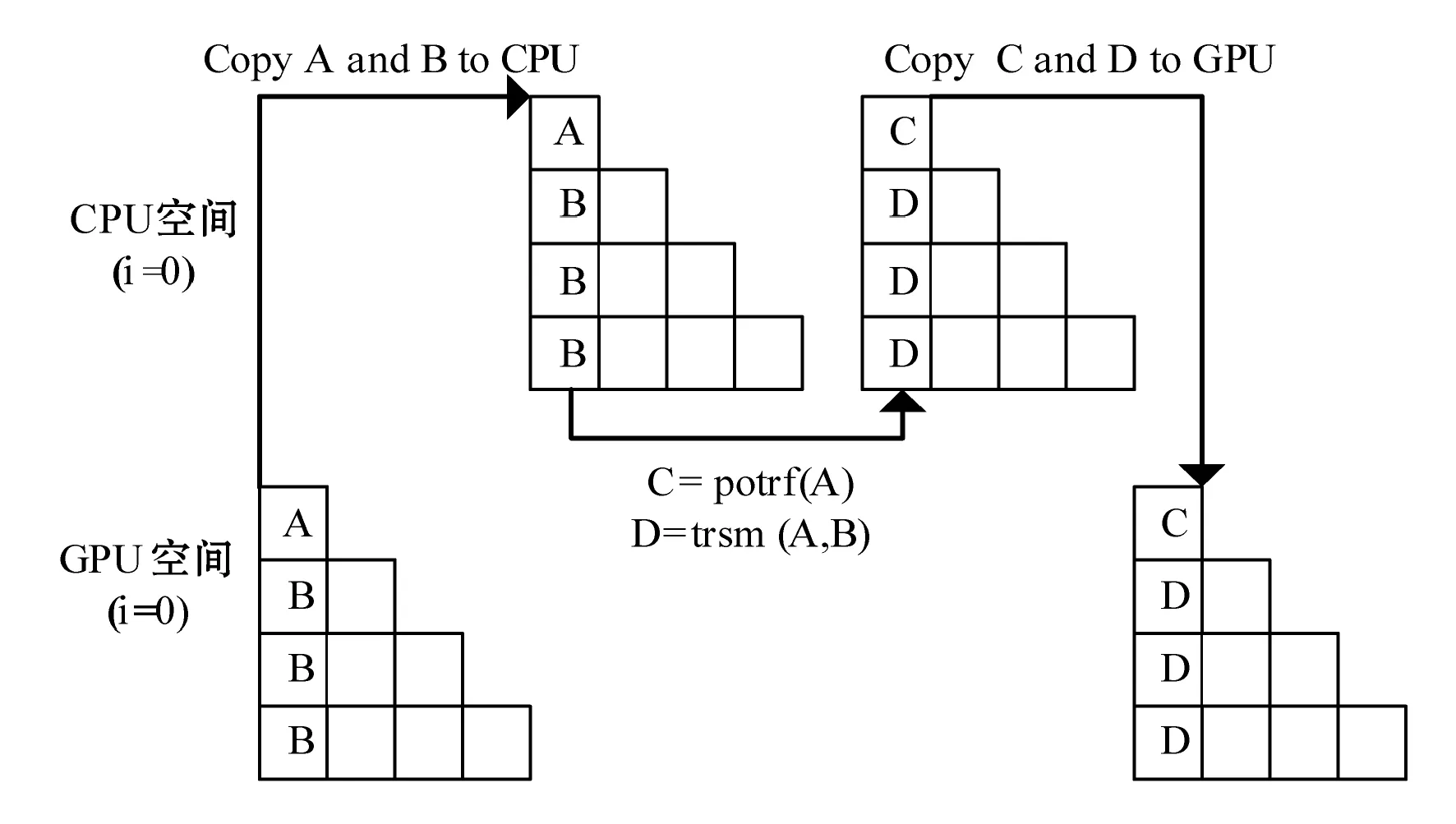
图3 第1步更新
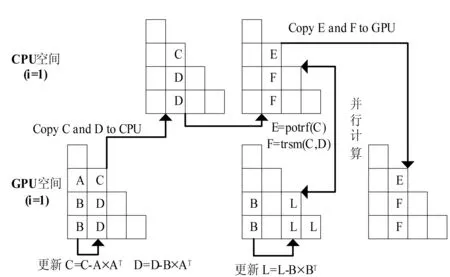
图4 第2步更新

图5 第3步更新
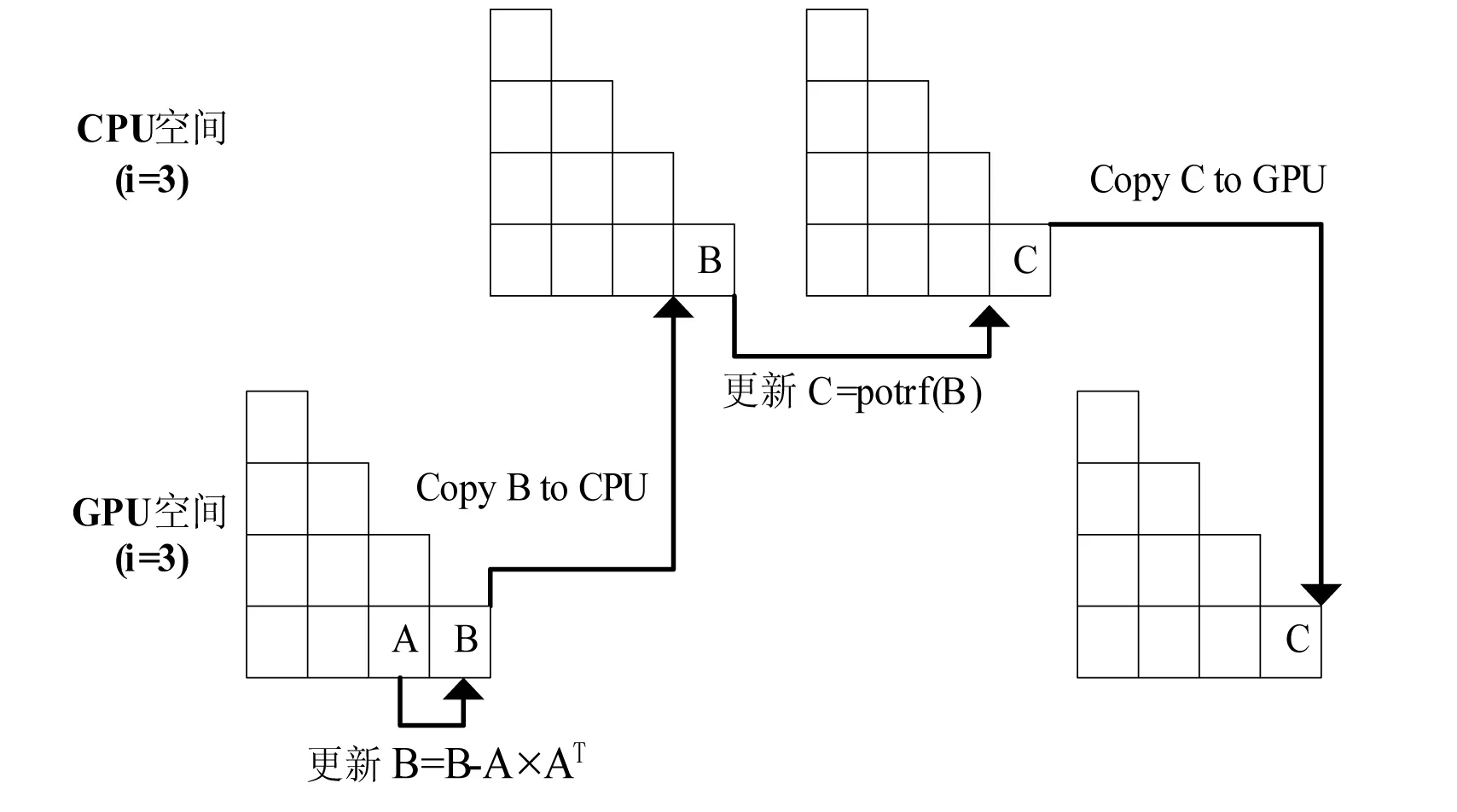
图6 第4步更新

图7 某次剩余矩阵
Volkov的混合算法巧妙地移动了矩阵循环的更新顺序,这样余部矩阵的上次更新和本次子块的Cholesky分解及其所在列的更新可以同时进行。
考察Volkov算法中的混合并行部分,对GPU上的某次迭代更新后,有如图7所示的剩余矩阵:
其中矩阵A1、A2、A3为剩余待更新矩阵,子块B1、B2为已求出的Cholesky分解部分。之后,在GPU上按如下公式对A1与A2进行更新:
A1=A1-B1×B1T
(10)
A2=A2-B2×B1T
(11)
然后将A1与A2异步传输到CPU。同时,在GPU上对余部矩阵按如下公式进行更新:
A3=A3-B2×B2T
(12)
在CPU上再次对A1和A2更新:
A1=potrf(A1)
(13)
A2=trsm(A1,A2)
(14)
其混合并行的示意如图8所示。
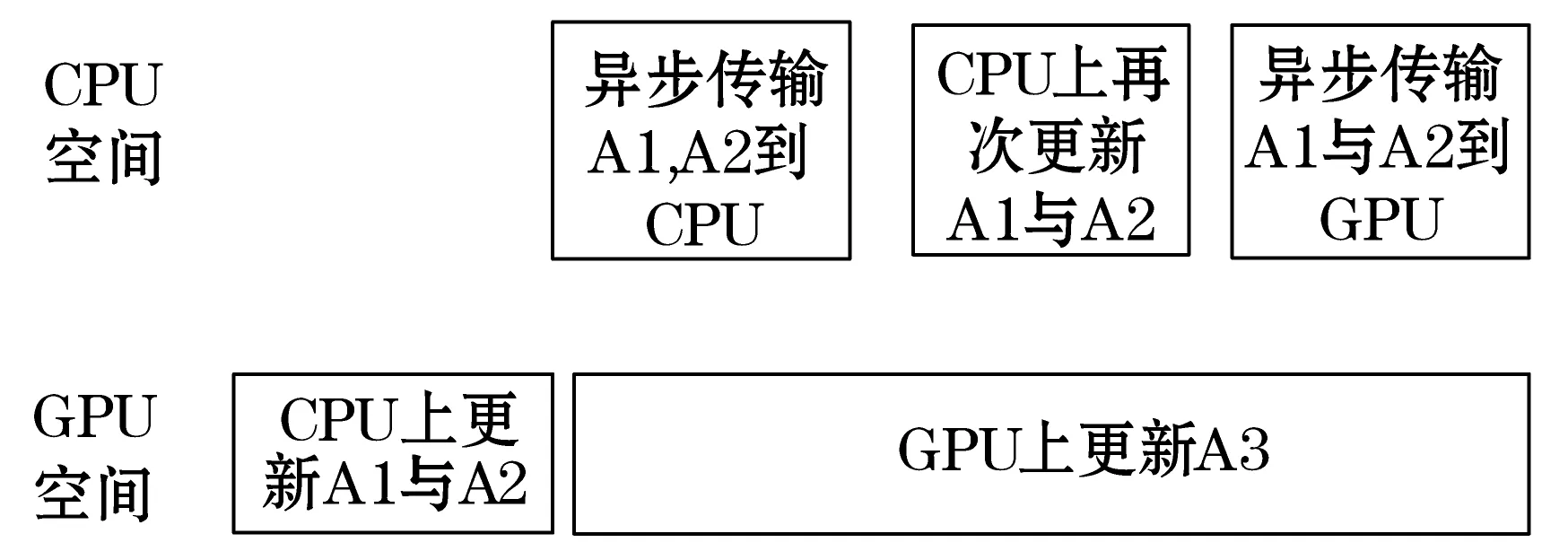
图8 原Volkov的混合调度策略
可以发现在GPU上更新矩阵A1、A2与更新A3是相互独立的。而且当剩余待更新矩阵阶数较大时,可以考虑将A1的首次更新移到CPU上进行。注意,对A2的两次更新不能同时移到CPU上进行,因为对A2的两次更新计算量都比较大,在CPU上计算时,耗时很多,极容易超过GPU上对A3的更新耗时,从而导致GPU的空闲。
此外,当剩余待更新的矩阵较小时,在GPU上更新A3的时间较短。此时不适合再将子矩阵A2转移到CPU上进行更新,否则会使得GPU出现长时间空闲。
整个混合计算过程中对数据传输采用异步方式,使得每次数据传输时间被GPU计算或CPU计算隐藏。
对此,我们综合考虑了计算的CPU以及GPU的计算性能,以Volkov的混合算法为基础,给出了一种新的调度策略。
2.4新的混合调度算法
记剩余待更新的矩阵A3的阶数为ns。将新的混合调度算法分为以下三个阶段:
阶段1当ns>x时,更新子矩阵A3耗时较长,因此CPU可以做更多的工作以减少空闲时间。由于对子矩阵块A2的两次更新只能有一次移到CPU上进行,故有以下2种调度策略:
1) 将A2的第一次更新放在GPU上执行,如图9所示。
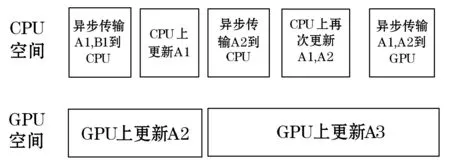
图9 阶段1的混合调度策略1
2) 将A2的第二次更新放在GPU上执行,如图10所示。

图10 阶段1的混合调度策略2
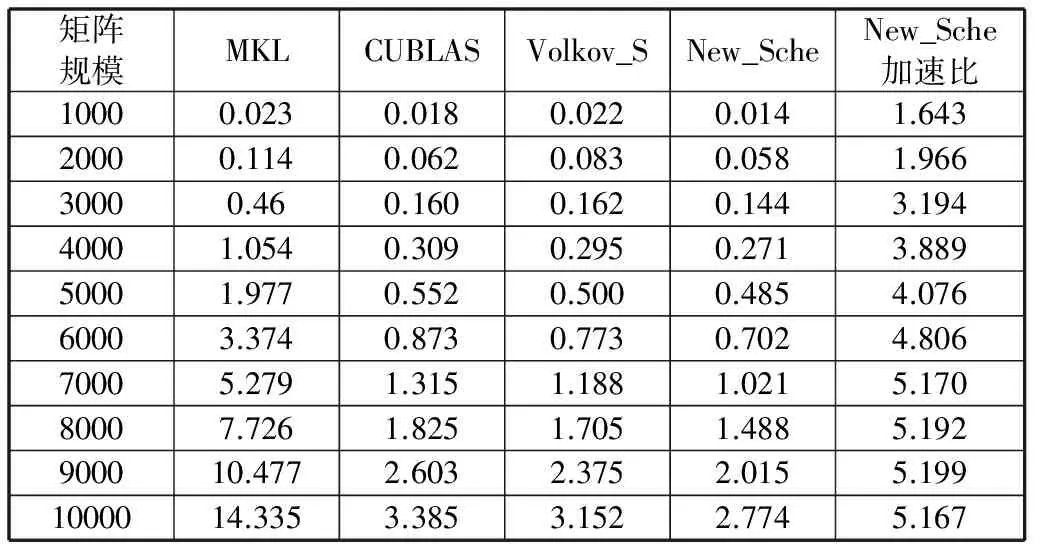
通过分析A2两次更新的计算量,可以发现A2的前次更新计算量为A2再次更新计算量的两倍。为防止GPU出现空闲,只有当ns>x1(x1>x)时,GPU上对A3的更新任务能完全隐藏CPU上的计算任务,采用混合调度策略2;否则,x 阶段2当y 阶段3当ns 图11 阶段3的混合调度策略 其中x与y的值需要依据各自计算的CPU和GPU的性能来大致确定,以保证GPU不会出现空闲时间并且CPU的空闲时间最小。这样的混合调度策略则是非常合适的。 同时,要对Volkov混合算法的第一步和最后一步进行调整。在第一步中,对第一主列块的更新与余部矩阵传输到GPU上可以异步进行,这样其中的一个耗时会被隐藏。最后一步更新时,可以先将最后一个子块先传回至CPU,然后将更新最后一个子块与传回剩余矩阵数据异步执行。 对于分块大小nb,可以参考MAGMA软件包中关于分块值的设定。针对Kerpler构架的GPU,可将分块值设定如下: (15) 3.1实验环境 本文中描述的GPU计算过程均是在NVIDIA的Kerpler构架的GPU上实现的。有关数值试验的硬件和软件平台见表1所示。 表1 实验环境 3.2实验结果与分析 实验测试1000~10 000阶对称正定矩阵,而且使用双精度数据类型,以保证计算结果的精确性。 首先分别给出本实验环境下MKL中执行dgemm以及dtrsm的耗时以及CUBLAS中一执行dgemm,dtrsm以及syrk的耗时的一个参考值,如表2所示。该数据用于估计划分阶段的x(包括x1)与y值。 表2 各函数测试结果(单位:毫秒) 其中针对dgemm函数,m为表格的第一列,n=k=512。而dtrsm与dsyrk函数的n为表格第一列,k=512。 表3给出了数据矩阵在CPU与GPU之间的传输耗时的一个参考值。 表3 数据传输测试(单位:毫秒) 下面考虑x=6000时,使用阶段1的混合调度策略1是合适的。首先依据表3可得到,异步传输A1,B1(矩阵规模均为512×512) 以及在CPU上更新A1的时间被GPU上更新A2隐藏。而异步传输A2(矩阵规模6000×512)耗时t1<20 ms,在CPU上再次更新A2耗时t2<80 ms,异步传回A1,A2耗时t3<20 ms,而GPU上对矩阵A2(规模6000阶)的更新耗时为t≈150 ms>(t1+t2+t3),故可取x=6000。类似,我们可以由此得到比较合理的x1,x以及y的值,分别如下: x1=8000x=6000y=4000 最后,对1000~10000阶对称正定矩阵分别使用4种方法进行计算。表4给出了4种方法计算1000~10 000阶对称正定矩阵的Cholesky分解的结果。其中可以看到基于新调度策略的函数New_Sche明显优于使用CUBLAS直接计算Cholesky分解以及基于Volkov的混合算法的函数Volkov_S。 表4 各算法测试结果(单位:秒) 科学计算中使用CPU与GPU混合并行计算的例子层出不穷,然而最困难的在于设计一种负载均衡的混合调度方案,从而使得CPU的空闲时间尽可能小,同时又不能让GPU空闲。糟糕的混合调度方案会使得整体计算性能下降,或者使得计算不正确,从而失去了混合计算的目的,这都是需要避免的。合适的混合调度策略往往需要依据自身计算机的CPU以及GPU的计算性能来共同确定。首先细致分析每步操作在CPU以及GPU上的计算速度,然后合理划分计算任务到CPU和GPU上执行。再者,算法中会大量使用异步传输操作,使得这些数据传输耗时被CPU和GPU上的计算时间隐藏,这也是优化加速的一个重要部分。最后,本文中没有考虑分块值对混合调度策略的影响。由实验的分析可知,分块值与调度策略有直接关系,影响阶段值x1,x以及y的确定。如何确定最优的分块值以及相应的调度策略将是后面要进行的工作。 [1] Chandrasekar J,Kim I S,Bernstein D S,et al.Reduced-Rank Unscented Kalman filtering using Cholesky-based decomposition[C]//American Control Conference,June,2008:1274-1279. [2] Yu H,Chung C Y,Wong K P,et al.Probabilistic Load Flow Evaluation With Hybrid Latin Hypercube Sampling and Cholesky Decomposition[J].IEEE Transactions on Power Systems,2009,24 (2):661-667. [3] David S.Watkins.Fundamentals of Matrix Computations[M].New York:John Wiley and Sons,2013. [4] Gene H Golub,Charles F,Van Loan.Matrix Computations [M].Baltimore:Johns Hopkins University Press,2013. [5] Volkov V,Demmel J W.Benchmarking gpus to tune dense linear algebra[C]//Proceedings of the 2008 ACM/IEEE Conference on Supercomputing,Nov,2008:1-11. [6] 胡鹏飞,袁志勇,廖祥云,等.基于CPU-GPU混合加速的SPH流体仿真方法[J].计算机工程与科学,2014,36(7):1231-1237. [7] 张健,焦良葆,陈瑞.CPU-GPU混合平台上动态场景光线跟踪的研究[J].计算机工程与应用,2012,48(21):151-154. [8] Yaohung M Tsai,Weichung Wang,RayBing Chen.Tunning Block Size for QR Factorization on CPU-GPU Hybrid Systems[C]//Proceedings of the IEEE 6th International Symposium on Embedded Multicore Socs,Sept,2012:205-211. [9] John Cheng,Max Grossman,Ty McKercher.CUDA C Programming[M].Indianalpois:John Wiley & Sons,2014. [10] 刘金硕,邓娟,周峥,等.基于CUDA的并行程序设计[M].北京:科学出版社,2014. ACCELERATING CALCULATION OF CHOLESKY FACTORISATION OF MATRIX WITH GPU Shen CongGao Huotao (School of Electronic Information,Wuhan University,Wuhan 430072,Hubei,China) A concrete implementation of Cholesky factorisation on graphic processing unit (GPU) for large real symmetric positive definite matrix is described in this article.We analyse the hybrid parallel algorithm presented by Volkov for computing the Cholesky factorisation in detail.On that basis,and according to the computational performances of CPU and GPU on our own computers,we present a more reasonable hybrid three-phase scheduling strategy,which further reduces the idle time of CPU and avoids the occurrence of GPU in idle status.Numerical experiment shows that the new hybrid scheduling algorithm achieves a speedup of more than 5 times compared with the standard MKL algorithm when the order of a matrix is larger than 7000,and it also observably outperforms the performance of original Volkov’s hybrid algorithm. GPUCholesky factorisationSpeedupHybrid algorithm 2015-04-10。湖北省自然科学基金重点项目(ZRZ20 14000286)。沈聪,硕士生,主研领域:并行计算。高火涛,教授。 TP361 A 10.3969/j.issn.1000-386x.2016.09.066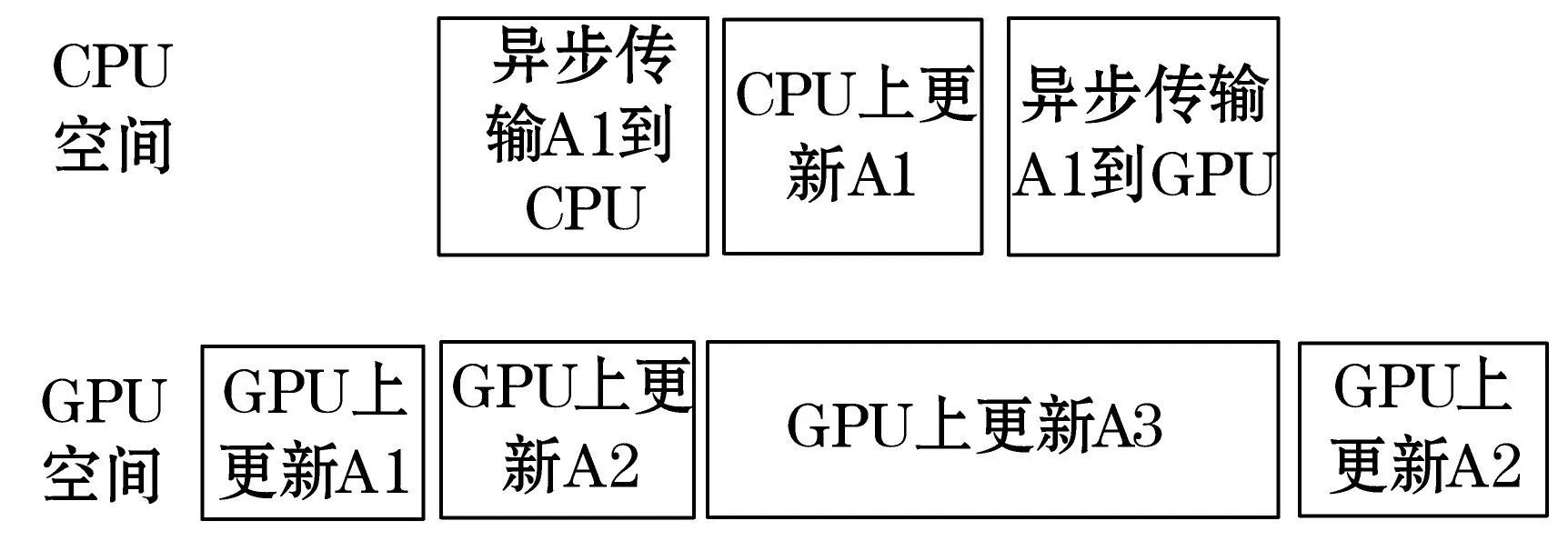

3 数值实验及结果分析



4 结 语
