基于新型扰动观测器的永磁同步电机滑模控制

白天明

(辽宁机电职业技术学院，辽宁 丹东　118001)



基于新型扰动观测器的永磁同步电机滑模控制

白天明

(辽宁机电职业技术学院，辽宁 丹东118001)

为了提高永磁同步电机(PMSM)调速系统的控制性能，提出了一种基于新型扰动观测器的滑模速度控制器。建立了包含参数不确定性及负载扰动的PMSM数学模型。为了减少扰动量的影响，设计了一种新型扰动观测器，并以此得到的观测值作为前馈量补偿到滑模控制器的输入端。仿真及试验结果表明，与传统PI控制器相比，该算法提高了系统的鲁棒性和动态响应速度。

永磁同步电机； PI控制； 滑模控制； 扰动观测器

0　引　言

随着生产技术的不断发展，人们对电机调速系统的调速范围、动静态性能等都提出了更高的要求。永磁同步电机(Permanent Magnet Synchronous Motor， PMSM)由于具有结构设计简单、运行效率高、功率密度高等优点，在军事和民用等领域得到了广泛的应用[1-2]。目前，关于PMSM调速系统的控制策略大多仍然采用传统的PI控制器，主要是因为该控制器具有结构简单且参数便于调节等诸多优点，在电气传动系统中得到了广泛应用。交流异步电机系统本身是一个比较复杂的非线性系统，为了便于控制器的设计，对电机的数学模型进行了简化处理。但是，当电机长时间运行或者受到外界扰动的影响时，电机的参数都会发生一定的变化，因此基于此简化模型得到的PI控制器参数并不能满足电机高性能控制的要求[3- 4]。

为了解决传统PI控制存在的缺点，随着现代控制技术的发展，一些先进的控制算法逐步被应用于PMSM调速系统。滑模控制(Sliding-Mode Control， SMC)由于其控制器设计简单、鲁棒性强等优点而被广泛应用[5-13]。但是，SMC对外界扰动和参数变化的抑制是通过设置较大的切换增益来实现的。切换增益的大小直接决定SMC算法的动态性能，但是较大的增益在提高系统收敛速度的同时，也会带来系统的抖振问题。另外，基于趋近律方法的传统滑模控制器设计方法仍然采用传统的趋近律方法，系统抖振现象比较严重。

为了解决上述问题，本文将PMSM在运行过程中参数的变化、参数的不确定性和突加负载扰动等效为总的扰动量，设计一种新型扰动观测器来观测系统中存在的干扰量，并用此观测值作为前馈量补偿到滑模控制器的输入端，从而提出了一种带有扰动观测器的滑模控制策略。最后仿真和试验结果都验证了该算法具有较好的动静态性能，证明了该算法的有效性和可行性。

1　PMSM的数学模型

建立d-q坐标系下表贴式PMSM的数学模型为[14-15]

(1)

式中：ud、uq，id、iq——分别为定子电压和电流；

R——定子电阻；

Ls——定子电感；

pn——电机的极对数；

ω——机械角速度；

ψf——磁链；

J——转动惯量；

TL——负载转矩；

Te——电磁转矩。

由于表贴式PMSM设计结构的特殊性，所以采用id=0的控制策略即可获得较好的控制效果。此时式(1)可简化为

(2)

为了便于控制器的设计，定义PMSM系统的状态变量：

(3)

式中：ωref——参考转速，并假定ωref存在二阶导数。

根据式(2)和式(3)可知：

(4)

当考虑电机的参数存在变化时，式(4)可表示为

(5)

式中： Δa，Δb，Δc——分别为对应项的不确定因素，且有界。

设g(t)为总的不确定量：

(6)

将式(6)和式(5)代入到式(3)，可得系统的数学模型：

(7)

2　基于干扰观测器的滑模控制器设计

2.1滑模速度控制器设计

为了便于速度控制器的设计，首先定义滑模面函数为

s=cx1+x2

(8)

式中:c>0为设计参数。

根据SMC的基本原理，传统的滑模控制器可设计为

u=ueq+uvs

(9)

uvs——切换控制，实现对参数变化和外界扰动的鲁棒控制。

则式(9)可满足：

(10)

为了分析如式(10)所示控制器的稳定性，定义Lyapunov函数为

(11)

对式(11)求导，并将式(8)和式(10)代入式(11)可得

(12)

2.2新型扰动观测器设计

为了进一步改善控制器的控制性能，消除扰动量对控制系统的影响，提出一种新的滑模控制器为

(13)

扰动观测器设计为

(14)

为了分析如式(14)所示控制器的稳定性，定义Lyapunov函数为

(15)

对V求导，并将式(14)代入得

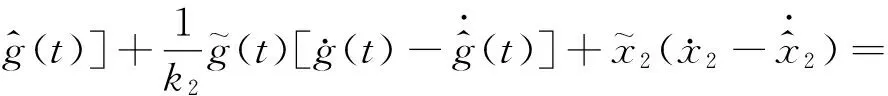
(16)

(17)

根据式(13)可求得滑模速度控制器的输出，即q轴的参考电流量为

(18)

从式(18)可以看出，由于积分器的作用，进一步削弱了抖振现象，提高了系统的动态品质。

3　仿真及试验结果分析

采用如图1所示的PMSM调速控制系统进行仿真与试验验证。

图1　PMSM调速系统控制框图

为了验证文中所提控制算法的有效性，首先在MATLAB/Simulink环境搭建系统的仿真模型，电机的具体参数如下： 定子电阻R=2.46Ω，定子电感Ls=6.35mH，永磁磁链ψf=0.175Wb，转动惯量J=1.02kg·m2，摩擦因数B=0.0001N·m·s，永磁磁链ψf=0.175Wb，极对数pn=4。其中，仿真条件设置为参考转速500r/min，在t=0.5s时刻突加负载转矩TL=50N·m。

为了便于比较分析，图2和图3分别给出了采用PI控制器和文中所提滑模速度控制器的仿真结果。其中，图2(a)和图3(a)分别给出了当突加负载时两种控制算法下的转速变化曲线；图2(b)、图2(c)和图3(b)、图3(c)分别给出了突加负载时电磁转矩和三相电流的响应曲线。

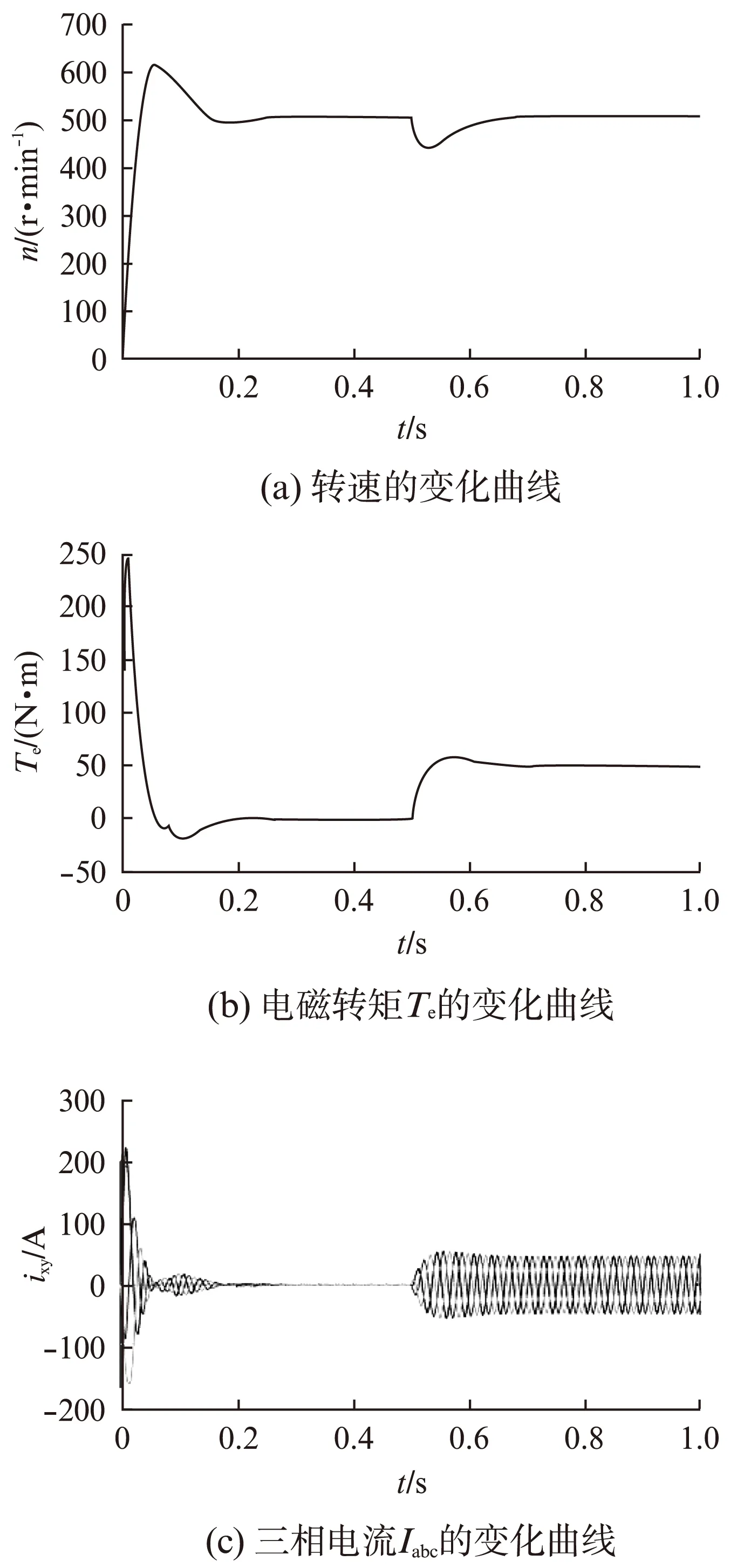
图2　基于PI速度控制器的仿真结果

图4和图5给出了采用图1所示的PMSM调速系统控制框图的试验结果。其中参考转速设定为500r/min，系统稳态运行后突加负载情况下的转速响应如图4(a)和图5(a)所示，系统稳定后突加负载时的转矩响应如图4(b)和图5(b)所示。

从以上仿真及试验结果可知： 采用PI速度控制器时，系统转速、电磁转矩均有较明显的波动，当施加外界扰动时，恢复到原有转速需要一定的调节时间，且存在稳态误差；而采用新设计的滑模速度控制器控制时，系统转速、转矩具有较好的动态性能，转速波动小，调节时间较短，抗外界扰动能力强，鲁棒性好，验证了该算法的可行性和有效性。

图3　基于滑模速度控制器的仿真结果

图4　基于PI速度控制器的试验结果

图5　基于滑模速度控制器的试验结果

4　结　语

为了提高PMSM调速系统的动态性能，本文提出了一种基于扰动观测器的滑模速度控制策略。在滑模控制器的基础上，同时为了减少扰动量的影响，设计了一种新型扰动观测器，并以此得到的观测值作为前馈量补偿到滑模控制器的输入端。通过与传统PI控制器进行比较，仿真及试验结果验证了该算法的可行性和有效性。

[1]袁雷，沈建清，肖飞，等.插入式永磁低速同步电机非奇异终端滑模观测器设计[J].物理学报，2013，62(3)： 37- 45.

[2]杨书生，钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计[J].中国电机工程学报，2009，29(3)： 84-89.

[3]NEE H P. Determination of d and q reactance of permanent-magnet synchronous motors without measurements of the rotor position[J]. IEEE Trans on Industry Applications， 2000，36(5)： 1330-1334.

[4]杨书生，钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计[J].中国电机工程学报，2009，29(3)： 84-89.

[5]王辉，万里瑞，王才东.基于智能滑模控制的永磁直线同步电机调速系统[J].电机与控制应用，2014，41(2)： 6-10.

[6]杨代利，张宏立.基于全鲁棒滑模控制的永磁同步电机伺服系统矢量控制[J].电机与控制应用，2014，41(2)： 19-22.

[7]苏良昱.基于PCHD模型和滑模控制的表贴式永磁同步电机控制系统设计[J].电机与控制应用，2015，42(8)： 39-43.

[8]钱荣荣，骆敏舟，赵江海，等.永磁同步电动机新型自适应滑模控制[J].控制理论与应用，2013，30(13)： 1414-1421.

[9]常雪剑，刘凌，崔荣鑫.永磁同步电机非奇异快速终端可变边界层滑模控制[J].西安交通大学学报，2015，49(6)： 53-59.

[10]卢涛，于海生，山炳强，等.永磁同步电机伺服系统的自适应滑模最大转矩/电流控制[J].控制理论与应用，2015，32(2)： 251-255.

[11]张晓光，赵克，孙力，等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报，2011，31(24)： 77-82.

[12]李政，胡广大，崔家瑞，等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报，2014，34(3)： 431- 437.

[13]汪海波，周波，方斯琛.永磁同步电机调速系统的滑模控制[J].电工技术学报，2009，24(9)： 71-77.

[14]GHAFARI-KASHANI A R， FAIZ J， YAZDANPANAH M J. Integration of non-linearH∞and sliding mode control techniques for motion control of a permanent magnet synchronous motor[J]. IET Electric Power Applications， 2010，4(4)： 267-280.

[15]LEE J H， ALLAIRE P E， GANG T， et al. Integral sliding-mode control of a magnetically suspended balance beam： analysis simulation， and experiment[J]. IEEE/ASME Transactions on Mechatronics， 2001，6(3)： 338-340.

Sliding Mode Control for Permanent Magnet Synchronous Motor Based on Novel Disturbance Observer

BAITianming

(Liaoning Mechatronics College， Dandong 118001， China)

A siding mode control(SMC) strategy with a novel disturbance observer was proposed for permanent magnet synchronous motor(PMSM). The mathematical model of PMSM composed of parameters uncertainty and disturbance was established， in order to estimate the disturbance caused by model parameters variation and load change， a novel disturbance observer was employed， and then this estimated value was used to construct a feed-forward compensation which was added to SMC input. All results showed that the arithmetic has the advantages of faster response， less stabilization error compared to traditional PI controller.

permanent magnet synchronous motor(PMSM)； PI controller； sliding mode control(SMC)； disturbance observer

白天明(1978—)，男，硕士研究生，高级工程师，研究方向为智能仪表、测控技术。

TM 351

A

1673-6540(2016)09- 0020- 05

2016-03-28