基于莱特准则和小波变换的遥测数据处理方法

孙永帅，王少云

（1.南京航空航天大学 电子信息工程学院，江苏 南京210016；2.南京航空航天大学 无人机研究院，江苏 南京210016）

基于莱特准则和小波变换的遥测数据处理方法

孙永帅1，王少云2

（1.南京航空航天大学 电子信息工程学院，江苏 南京210016；2.南京航空航天大学 无人机研究院，江苏 南京210016）

遥测数据经常含有噪声和野值，针对遥测数据的处理面临的消除噪声和野值剔除问题，介绍了小波变换的基本原理以及小波消噪在信号处理方面的应用，提出了利用莱特准则和小波软阈值消噪相结合的方法进行野值剔除，利用MATLAB软件进行遥测信号噪声消除和野值剔除仿真试验，结果表明该方法具有良好的降噪效果和出色的野值剔除能力。

遥测数据；小波变换；野值剔除；降噪；阈值

在靶场外弹道测量动态目标时，由于随机误差和各种干扰的存在，测量数据中往往包含严重偏离目标真值的数据点，这些严重偏离目标真值的数据就是所谓的“野值”。野值的特点是幅值大，持续时间短，无规律［1］。如果不予以分离和剔除这些野值，则给数据处理带来很大的误差，严重影响处理结果的精度，无法准确地反映武器系统的飞行特性，因此必须将它们全部剔除．本文提出一种基于小波变换的野值剔除方法。

1 基本理论

1.1 小波变换理论

小波变换主要讨论R上平方可积分函数构成的函数空间L2（R），若小波函数φ（t）∈L2（R），需要满足如下容许条件［2］：

设s（t）是平方可积分函数，则它的连续小波变换定义为：

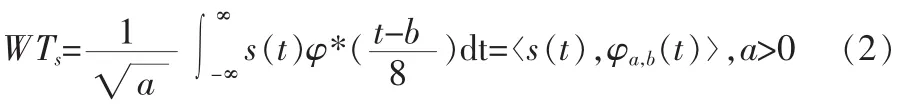
式中φa，b（t）为小波变换的基函数，它是通过窗函数φ（t）时间平移b，尺度伸缩a得到的。常数a和b分别称为尺度参数和平移参数，若尺度参数a变大，基函数窗口时宽增大，时域分辨率降低，频域分辨率提高；若尺度参数a变小，基函数窗口时宽缩小，时域分辨率提高，频域分辨率降低，所以小波变换既能对信号的高频成分进行精确分析［3］，也可以对信号低频成分精确分析，小波变换的这种多分辨率特性使其在信号处理方面得到了广泛的应用，文中将小波变换应用于实时遥测数据野值剔除工作。

1.2 野值的判别与剔除

根据莱特准则，当观测数据服从正态分布时，残差落在3倍标准差［-3σ，3σ］的概率超过99.7%，落在此区域外的概率不超过0.3%，因此，可以认为残差落于该区域外的测量数据为野值［4］。假设1组观测序列为x（i）（i=1，2，…，N），在x（k）中存在野值数据点。利用莱特准则剔除野值首先要计算该组观测数据的算术均值［4］

再计算其标准差σ

根据原始观测序列x（i）和算术均值计算数据残差xb（i）

将残差xb（i）逐一与3倍标准差进行比较，进行野值检验。如果|xb（i）|≥3σ，则与xb（i）对应的观测数据x（i）为野值，应予以剔除，对于判定为野值的点，如果直接置零，可能会引入更大的误差，文中采用以野值前一个样本值替换野值的方法，循环检测并剔除野值，直至样本信号中所有野值被剔除。

1.3 小波去噪方法

小波去噪方法有3种。

1）强制去噪

该方法把小波分解中的高频分量强制为零，即丢弃所有高频分量的信息，再对信号进行小波重构，计算简单，而且得到的信号比较平滑，但是这种方法在消除噪声的同时有可能损失掉信号的重要细节。

2）阈值去噪

阈值去噪包含硬阈值去噪和软阈值去噪。

硬阈值去噪法：

软阈值去噪法：

其中x为高频系数，dm（x）为阈值量化后的高频系数，阈值，硬阈值去噪法针对每一层的高频分量都求得一个阈值，将绝对值小于等于阈值的高频系数置零，绝对值大于阈值的高频系数不做处理直接保留［5］。硬阈值去噪法操作简单，但容易引起伪吉布斯效应。软阈值去噪法将绝对值小于等于阈值的高频系数置零，绝对值大于阈值的正高频系数减去阈值，绝对值大于阈值的负高频系数加上阈值，使用软阈值量化后的高频系数对信号进行重构，得到的信号相对比较平滑。

3）模极大值去噪

模极大值去噪法利用李普希兹（Lipschitz）指数求出每个尺度上小波变换系数对应的模极大值点，不同尺度层的模极大值采用不同的阈值进行处理，根据保留下来的模极大值的位置重构小波系数，利用重构的小波系数进行小波反变换得到消除噪声的信号［6］。

2 理论分析与仿真

文中选取正弦信号作为原始信号，记为s（n），该信号幅度为2，角频率为0.03 rad/s，采样点数为1 000。向s（n）中加入高斯白噪声和野值点，作为待处理含噪声信号，记为sn（n），如图1所示，可以看出，该信号中包含随机噪声以及随机产生的野值。

2.1 直接使用小波软阈值去噪

对信号s（n）直接使用小波软阈值去噪法所得到的处理效果如图2所示，在不含有野值的区间，小波软阈值降噪效果良好，在出现野值的位置，虽然野值的幅度有所降低，小波软阈值去噪并没有消除野值，而且野值附近还存在波动，因此直接使用小波软阈值降噪法不能不能满足此类遥测信号处理要求。

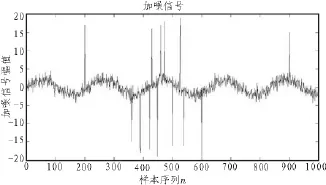
图1 加入白噪声和野值的信号

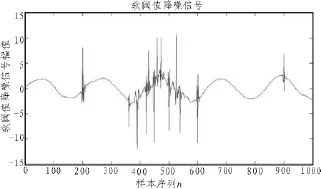
图2 直接使用小波软阈值降噪的处理效果

2.2 莱特准则剔除野值

针对图1中含有白噪声和野值的信号使用莱特准则进行野值判别，对于判定为野值的点，使用该样本点的前一个样本点替换野值，循环多次使用莱特准则判别并替换野值，直到莱特准则判定信号中无野值，经过莱特准则循环多次剔除野值后的信号如图3所示，可以看出较为明显的野值点已经被剔除，波形大体显示为正弦波，由于莱特准则只适用于野值判别，对信号中存在的大量的噪声则无能为力。

3 莱特准则和小波变换遥测数据处理方法

由以上仿真分析可知，莱特准则能够比较准确的判别野值，小波软阈值去噪能够有效的去除高斯白噪声，结合两种方法的特点，文中提出使用莱特准则与小波软阈值去噪相结合的方法对遥测数据进行处理，将该方法称为LW （Letts and Wavelet）遥测处理方法。

LW遥测处理方法分为4个步骤：

1）使用莱特准则对含噪声信号剔除野值；

2）对剔除野值的信号进行5层小波分解，得到近似分量和高频分量；

3）使用小波软阈值去噪法对1～5层高频分量进行降噪处理；

4）小波反变换重构信号。

图3为循环多次使用莱特准则剔除野值后的信号，可以看出幅值较大的野值点已经被剔除掉，图中所表现出的波动可以近似视为高斯白噪声，下一步可以使用小波多尺度分解，文中将图3中的信号进行5层分解，得到每层的近似分量和细节分量，如图4所示，有用信号包含在左侧的近似分量部分，噪声包含在右侧的细节分量部分，但细节分量还包含原信号中的高频信息，不可以直接将细节分量强制置零，否则会损失原始信号的细节，往往这些细节对数据分析工作至关重要，用小波软阈值去噪法对每个尺度上的细节分量进行降噪处理后，利用塔式重构算法进行小波重构即可得到剔除野值并去除噪声的近似原始信号［7］，LW遥测数据处理方法处理效果如图5所示。

从图5中可以看出，最终效果曲线比较平滑，逼近原正弦曲线，含噪声信号中的野值已经剔除，高斯白噪声也已经消除，处理效果能够满足数据分析要求。

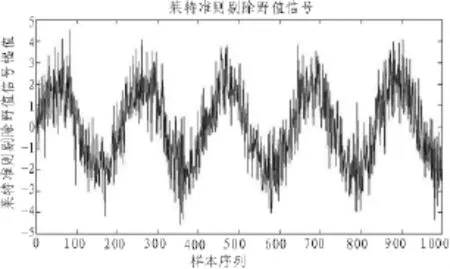
图3 莱特准则剔除野值的信号

图4 小波多尺度分解

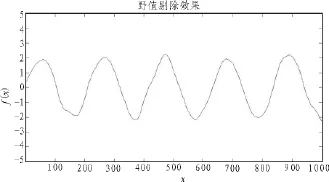
图5 LW方法处理效果

4 结束语

文中针对遥测信号含有噪声和野值的情况，对莱特准则判别野值的性能和小波软阈值去噪法进行MATLAB仿真分析，得出莱特准则具有出色的野值判别性能，小波软阈值去噪具有良好的白噪声消除性能［8］，提出了基于莱特准则和小波变换的遥测数据处理方法，并进行了理论分析和MATLAB实验仿真，证明了这一方法的有效性，该方法提高了遥测数据处理和分析的效率，可满足遥测数据事后处理要求。

［1］李保霖，赵建川，蔺文彬.小波分析在信号降噪中的应用［J］.电子设计工程，2015，23（6）:41-44.

［2］姜大治，常兴华.基于偏差估计的弹道异常值剔除方法［J］.战术导弹技术，2013（3）:71-75.

［3］Al Mutawa，J.Identification of errors-in-variablesmodel with observation outliers based on minimum-covariance-determinant［C］//Proceedings of the American Control Conference，Proceedings of the 2007 American Control Conference，2007．

［4］司祯祯.傅里叶变换与小波变换在信号去噪中的应用［J］.电子设计工程，2011，19（4）:155-157.

［5］徐利娜，陈俊彪，穆高超.靶场外弹道数据处理中的实时野值剔除算法［J］.应用光学，2012，33（1）:90-95.

［6］PARK JS，LEE SW.An example-based face hallucination method forsingle-frame，low-resolution facial images［J］.IEEE Transaction on Image Processing，2008，17（10）:1806-1816.

［7］卢元磊，何佳洲，安瑾，等.几种野值剔除准则在目标预测中的应用研究［J］.指挥控制与仿真，2011，33（4）：98-102.

［8］马志刚.基于小波分析的车辆噪声特征提取方法研究［J］.电子设计工程，2010，18（1）：3-7.

The processingmethod of telemetry data based on letts criterion and wavelet transform

SUN Yong-shuai1，WANG Shao-yun2
（1.College of Electronic and Information Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；2.UVA Research Institute，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Since noise and outliersare often contained in telemetry data，telemetry data processing is faced with the problem of Gaussian noise removing and outliers eliminating.The basic principle of wavelet transform and the application of wavelet transform in signal processing are introduced.The application of Letts criterion combined with wavelet transform in signal processing is introduced.The results show that themethod has good noise reduction effect and excellent outliers eliminating ability by using MATLAB software.

telemetry data；wavelet transform；outliers eliminating；noise reduction；threshold

TN911.72

A

1674－6236（2016）20-0082-03

2015-10-19 稿件编号：201510121

孙永帅（1989—），男，山东临沂人，硕士研究生。研究方向：遥控遥测。