基于可靠度的再生混凝土梁最小配筋率研究

张凯建， 肖建庄, 2， 丁　陶， 胡　博

(1.同济大学 土木工程学院，上海 200092； 2.同济大学 土木工程防灾国家重点实验室，上海 200092)



基于可靠度的再生混凝土梁最小配筋率研究

张凯建1， 肖建庄1, 2， 丁陶1， 胡博1

(1.同济大学 土木工程学院，上海 200092； 2.同济大学 土木工程防灾国家重点实验室，上海 200092)

为考察再生混凝土强度变异性对再生混凝土梁最小配筋率的影响，以普通混凝土梁最小配筋率为参照，保持规范目标可靠指标不变，分析了再生混凝土梁受弯时的最小配筋率和受剪时的最小配箍率，并将结果与普通混凝土梁进行了对比.分析结果表明，再生混凝土梁受弯时，由于钢筋的存在，再生混凝土强度的变异性对其受弯承载力变异性的影响较小，再生混凝土梁的最小配筋率提高很小.对于再生混凝土梁受剪，当再生混凝土强度变异系数为0.2时，C30再生混凝土梁的最小配箍率为0.17%，相比较普通混凝土梁约增加32.0%.通过合理增加配筋可以保证再生混凝土梁的受弯、受剪可靠指标与普通混凝土梁一致.

再生混凝土； 梁； 强度变异性； 最小配筋率； 最小配箍率； 可靠指标

再生混凝土相比较普通混凝土，最大的区别是再生骨料来源的不确定性导致的材料力学性能离散性有所增大[1-2].在构件层次，再生混凝土强度变异性的提高会导致再生混凝土构件的可靠度降低.为推动再生混凝土应用于实际工程，有必要对再生混凝土构件的设计参数进行研究.对于普通混凝土梁的最小配筋率，屈文俊等[3]对比分析了各国混凝土设计规范中在非抗震情况和抗震情况下混凝土受弯构件中受拉钢筋最小配筋率的规定及确定方法.何政等[4]对配有FRP(fiber reinforced polymer)筋的普通混凝土梁正截面受弯进行了分析，并给出了FRP筋的材料分项系数.Breccolotti等[5]对再生混凝土的抗压强度进行了试验研究，并对作用不同偏心矩的再生混凝土柱的受压可靠度进行了分析，给出了材料分项系数与再生粗骨料取代率的关系.但是，关于再生混凝土梁最小配筋率的研究还比较少.本文将基于可靠度理论对再生混凝土梁的最小配筋率和配箍率进行定量分析.

1　再生混凝土梁受弯最小配筋率

1.1钢筋及混凝土强度数据

对于普通混凝土受弯构件，屈服弯矩等于开裂弯矩时所对应的配筋率为最小配筋率，该数值可以通过力矩平衡的方法得到[3].现行《混凝土结构设计规范》[6]规定最小配筋率ρmin为

(1)

式中：ft为混凝土抗拉强度设计值；fy为钢筋抗拉强度设计值.若ρmin<0.2%，取ρmin=0.2%.由于按式(1)配筋时，梁的受弯破坏已经是延性破坏，因此在下面的计算中，按式(1)确定普通混凝土的最小配筋率.

对于再生混凝土，其强度的变异性要大于普通混凝土[7-8]，这会导致再生混凝土构件可靠指标降低，为使再生混凝土构件达到与普通混凝土构件相同的目标可靠指标，通常有以下几种方式：保持混凝土强度不变，提高配筋率；保持配筋率不变，提高混凝土强度值；同时提高配筋率和混凝土强度值.在配合比设计中，通过合理降低水灰比，再生混凝土强度(包括抗拉强度和抗压强度)的均值可以达到与普通混凝土相同的水平.因此，本文假定再生混凝土的强度均值与普通混凝土相同，分析再生混凝土梁最小配筋率和配箍率的变化.

表1,2分别列出了普通混凝土和钢筋的强度数据，包括强度均值、标准值、设计值及变异系数等.立方体均值是根据文献[9]确定的.本文假定再生混凝土抗压强度与抗拉强度的变异系数相同，进而可由普通混凝土抗拉强度的设计值计算得到其均值.

表1　普通混凝土强度数据Tab.1　Data of natural concrete strength

注：数据来源于文献[6,9].

表2　钢筋强度数据Tab.2　Data of reinforcement strength

注：数据来源于文献[6,10].

1.2极限状态方程的建立

《工程结构可靠性设计统一标准》[11]规定，按承载力极限状态设计时，普通混凝土梁发生延性破坏的目标可靠指标β=3.2.下面将基于再生混凝土和普通混凝土梁受弯时具有相同目标可靠指标这一标准进行再生混凝土梁受弯最小配筋率的计算，在计算过程中荷载效应保持不变.

混凝土梁的抗弯承载力可表示为

(2)

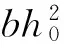
(3)

(4)

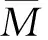
为保证采用不同强度等级混凝土(C20—C55)，配置不同强度钢筋的混凝土梁具有相同的可靠指标β=3.2，首先将最小配筋率ρmin，混凝土轴心抗压强度均值fcm，钢筋抗拉强度均值fym代入式(4)，计算受弯承载力均值，然后根据可靠指标等于目标可靠指标，进行迭代计算可以求出荷载效应均值.此处荷载效应均值的意义是，当在配置最小配筋率的梁内产生上述荷载效应时，梁的受弯可靠指标为3.2.因此，只需关注荷载效应值，而不必考虑再生混凝土梁上作用的恒载和活载的具体细节.普通混凝土和钢筋的强度设计值是固定的，可将荷载效应均值与规范设计抗力(用强度设计值计算得到的受弯承载力值)的比值计算出来，设为参数αb，如表3所示.

表3　参数αb取值表Tab.3　Value of αb

建立功能函数为

(5)

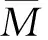
(6)

需要注意的是，外荷载并不取决于材料性能，此处只是用材料强度设计值来表示单位荷载效应的均值.

混凝土抗压强度和钢筋抗拉强度为独立变量，假定服从对数正态分布[5]，其均值与变异系数见表1和表2.

1.3数据计算及拟合

可靠指标采用JC法计算，计算过程如下：① 输入基本参数(如混凝土抗压强度均值和变异系数，钢筋抗拉强度均值及变异系数，最小配筋率，荷载效应变异系数等)；② 计算荷载效应并建立功能函数；③ 计算可靠指标；④ 判断计算可靠指标与目标可靠指标之差是否满足精度(2×10-4)要求；⑤ 若是，输出再生混凝土梁最小配筋率ρR,min=ρmin；⑥ 若否，则ρmin=ρmin+Δρ，返回到②.上述过程每完成一次，可以得到与混凝土抗压强度变异系数所对应的最小配筋率，直至计算得到所有的最小配筋率.程序框图如图1所示.

图1　最小配筋率计算程序框图Fig.1　Flowchart for calculating minimum reinforcement ratio

为使再生混凝土梁与普通混凝土梁的最小配筋率具有类似的表达形式，取再生混凝土梁最小配筋率表达式为

(7)

式中,ηb为配筋率系数，对应于普通混凝土的0.45，由于再生混凝土的设计值本文没有涉及，最小配筋率表达式中，ft为普通混凝土抗拉强度设计值.图2只列出了C30和C40混凝土梁分别配置HRB335和HRB400钢筋的拟合结果，HRB335-C30表示采用混凝土强度等级为C30、钢筋为HRB335的再生混凝土梁.图中点为计算得到的原始数据，曲线为拟合的结果.利用MATLAB进行数据拟合，采用以下表达式：

(8)

式中:a，b均为待定系数;δfc为再生混凝土抗压强度变异系数.

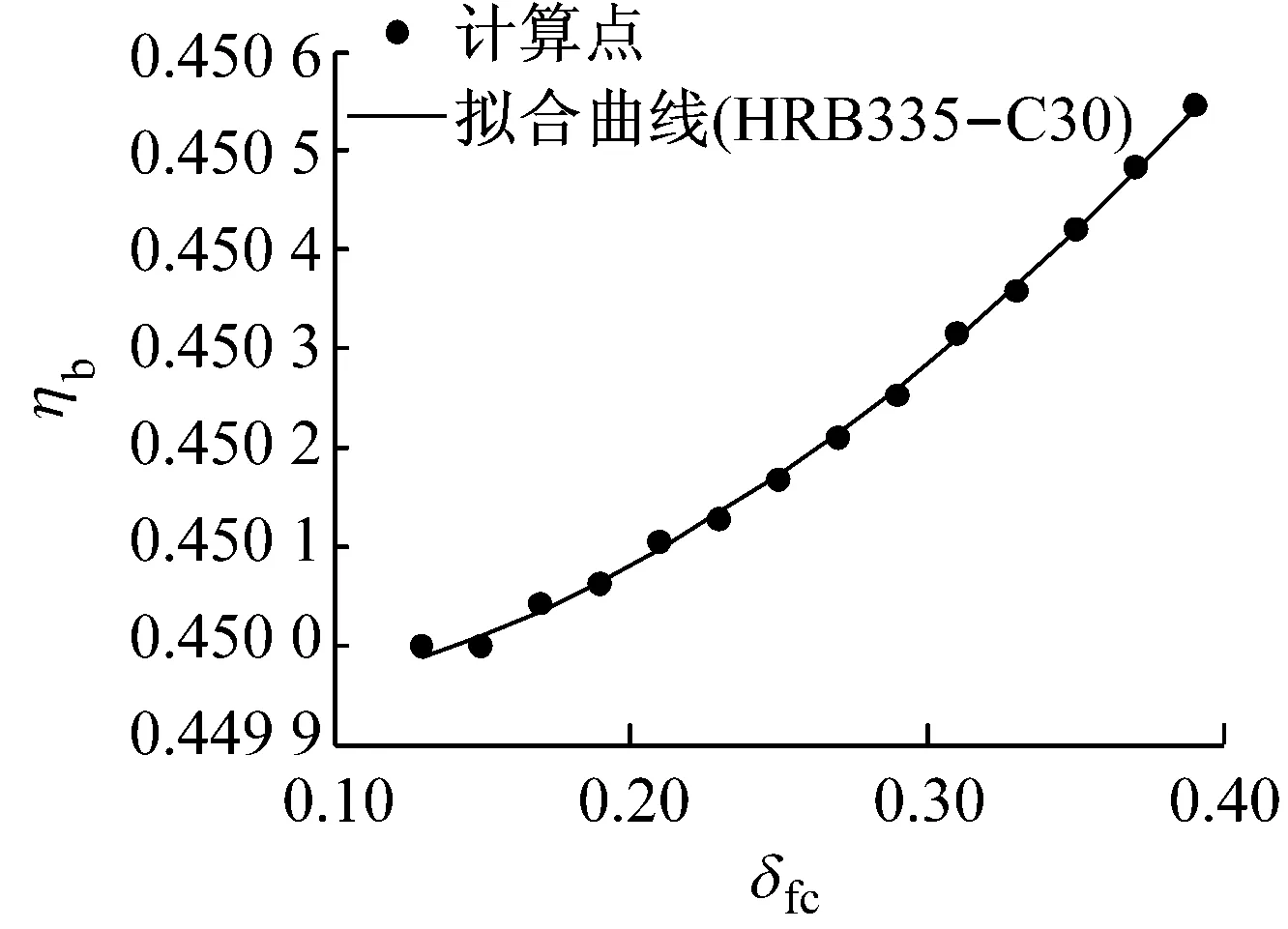
a HRB335-C30配筋率系数

b HRB400-C40配筋率系数图2　数据拟合曲线Fig.2　Fitting of data

混凝土强度等级为C20—C55，钢筋为HRB335和HRB400，共计对16根再生混凝土梁进行了分析.梁的最小配筋率拟合系数a，b及R2的计算结果见表4.

表4　系数a，b及R2的计算结果Tab.4　Calculation results of a，b and R2

通过表4可知，采用式(8)进行拟合的效果是比较好的，系数a约等于0.45，系数b变化较大.以计算的所有最小配筋率的数值进行拟合，取其上包络线，设γb=ηb/0.45，可以理解为配筋率放大系数.以下式进行拟合：

(9)

得到a1=1.0，b1=0.014.拟合的结果见图3.

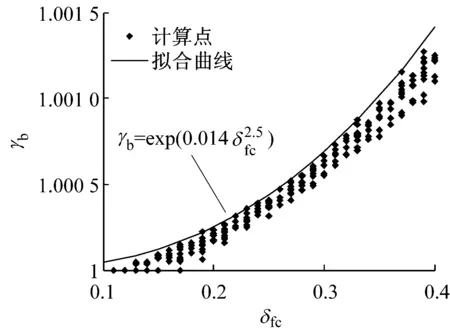
图3　再生混凝土梁最小配筋率放大系数Fig.3　Amplification coefficient of minimum reinforcement ratio of RAC beams

由图3可知，随着再生混凝土抗压强度变异系数的增加，配筋率放大系数以指数形式增长.极端情况下，当变异系数为0.35时，再生混凝土梁的最小配筋率相比较普通混凝土梁约增加0.1%.为考察其中的原因，以再生混凝土梁的配筋率和再生混凝土抗压强度的变异系数为变量，利用MATLAB软件产生混凝土强度和钢筋强度的随机数各100 000组，对梁的抗力参数进行计算，混凝土梁采用C30混凝土，配置HRB335钢筋.单位抗力的均值和变异系数如图4所示，图中Mu,max为受弯承载力最大值，δMu为受弯承载力变异系数.

通过对其他不同强度等级混凝土梁的抗力进行统计，得出的曲线和曲面类型与图4类似.图4a显示，梁的抗力随配筋率的增加呈抛物线增加，增加的速率在降低.统计结果表明，受弯承载力的变异系数小于再生混凝土抗压强度的变异系数.由图4b可知，当再生混凝土梁的配筋率为最小配筋率时，由于钢筋的存在，再生混凝土强度的变异性对抗力的变异性影响有限，因而导致再生混凝土梁的最小配筋率较普通混凝土梁提高很小.由于钢筋能够限制再生混凝土抗压强度的变异性对抗力变异性发挥作用，随着再生混凝土变异系数的增大，再生混凝土梁的可靠指标下降幅度有限，仅需增加少量的配筋就可以使再生混凝土梁的可靠指标达到普通混凝土梁的水平.当配筋率为1.0%时，梁的抗弯承载力的变异系数相比较最小配筋率时变化也不大.

a 受弯承载力与配筋率的关系曲线

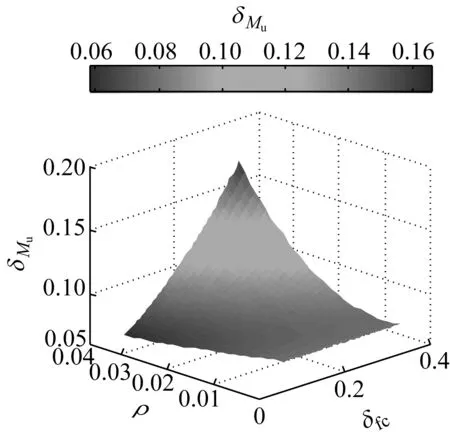
b 受弯承载力变异系数图4　受弯承载力统计参数Fig.4　Statistical parameters of flexural capacity

2　再生混凝土梁受剪最小配箍率

2.1极限状态方程的建立

对于普通混凝土梁受剪，《混凝土结构设计规范》[6]规定最小配箍率为

(10)

《工程结构可靠性设计统一标准》[11]规定，按承载力极限状态设计时，普通混凝土梁发生脆性破坏的目标可靠指标β=3.7.

考虑作用有均布荷载的混凝土梁，箍筋采用HPB300，其受剪承载力可表示为

Vu=0.7ftbh0+fyAsvh0/s

(11)

式中:Vu为梁受剪承载力；Asv为箍筋面积；s为箍筋间距.将公式两边同时除以bh0，得到

(12)

(13)

按照与计算再生混凝土梁受弯最小配筋率相同的思路进行计算.为保证采用不同强度等级混凝土(C20—C55)，配置HPB300钢筋的梁具有相同的可靠指标β=3.7，首先将最小配箍率ρsv,min，混凝土轴心抗拉强度均值ftm，钢筋抗拉强度均值fym代入式 (13)，计算受剪承载力均值，然后根据可靠指标都等于目标可靠指标，进行迭代计算可以求出荷载效应均值.经计算，可以得到荷载效应均值与规范设计抗力的比值，设为参数αs，如表5所示.

表5　参数αs取值表Tab.5　Value of αs

建立功能函数为

(14)

(15)

2.2数据计算及拟合

为保证再生混凝土梁与普通混凝土梁的最小配箍率具有类似的表达形式，取再生混凝土梁最小配箍率表达式为

(16)

式中,ηs为配箍率系数，对应于普通混凝土的0.24.图5给出了配置HPB300钢筋，混凝土等级为C30和C40梁的最小配箍率计算数据及拟合结果.HPB300-C30表示采用混凝土强度等级为C30，箍筋为HPB300的再生混凝土梁.采用以下二次多项式进行数据拟合：

(17)

式中:a2，b2，c2均为待定系数;δft为再生混凝土抗拉强度变异系数，取再生混凝土抗拉、抗压强度变异系数相等.

a HPB300-C30配箍率系数

b HPB300-C40配箍率系数图5　数据拟合曲线Fig.5　Fitting of data

混凝土强度等级为C20—C55，钢筋为HPB300，共计对8根再生混凝土梁进行了分析.梁的最小配箍率拟合系数a2，b2，c2及R2的计算结果见表6.

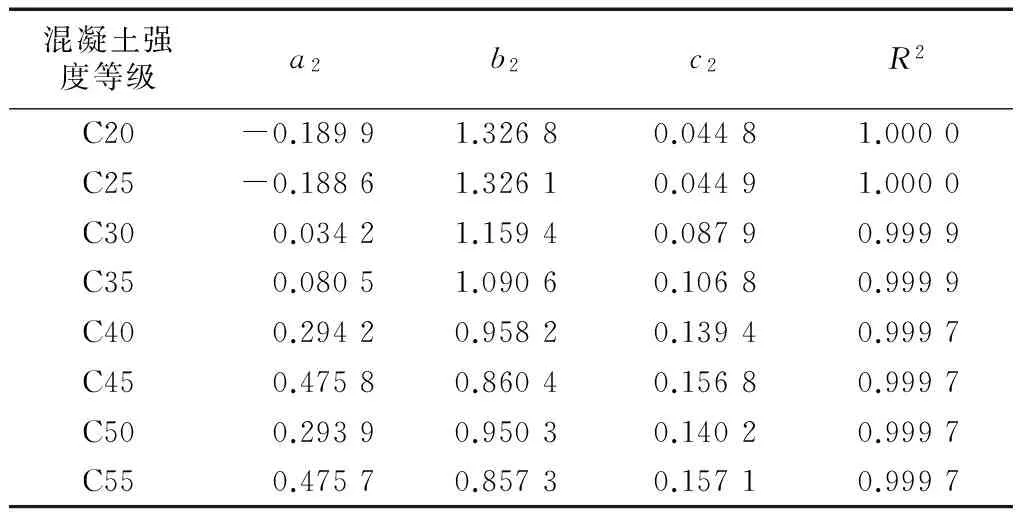
表6　系数a2，b2，c2及R2的计算结果Tab.6　Calculation results of a2, b2, c2 and R2

通过表6可知，采用式 (17) 进行拟合的效果是比较好的.参照再生混凝土梁受弯数据拟合的方法，以计算的所有最小配箍率的数值进行拟合，取其上包络线，设配箍率放大系数γsv=ηs/0.24，用下式进行拟合：

ρR,sv,min=γsv×0.24ft/fy=

(18)

得到a3=2.12，b3=3.55，c3=0.64.拟合结果见图6.

从图6可知，随着再生混凝土抗压强度变异系数的增加，最小配箍率放大系数γsv呈抛物线增长.梁的混凝土强度等级为C30，箍筋为HPB300，当变异系数为0.2时，再生混凝土梁的最小配箍率相比较普通混凝土梁约增加32.0%.以再生混凝土梁的配箍率和再生混凝土强度的变异系数为变量，同样，利用MATLAB软件产生混凝土抗拉强度和钢筋抗拉强度的随机数各100 000组，按照式(13)计算单位抗力的均值，对梁的受剪承载力参数进行统计计算.单位抗力的均值和变异系数如图7所示，Vu,max为受剪承载力最大值，δVu为受剪承载力变异系数.

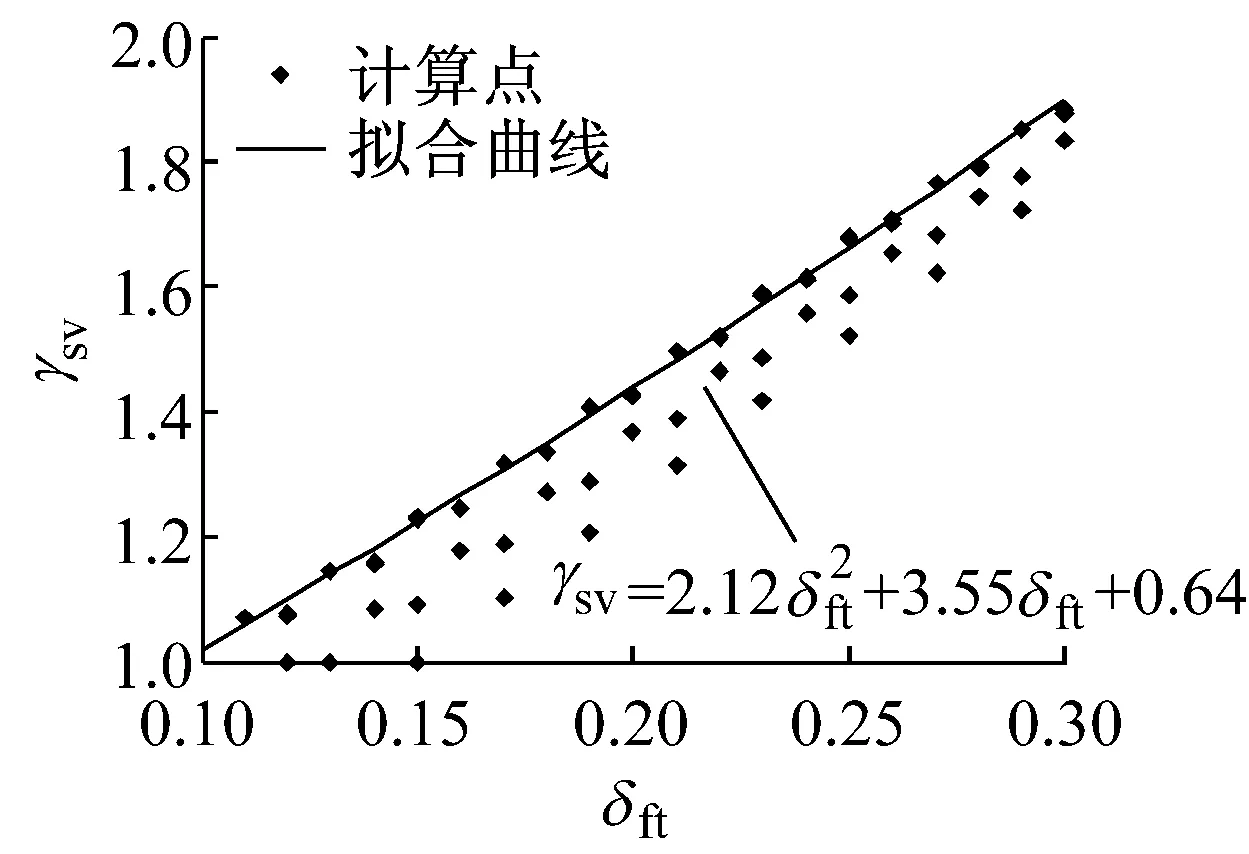
图6　再生混凝土梁最小配箍率放大系数Fig.6　Amplification coefficient of minimum stirrup ratio of RAC beams

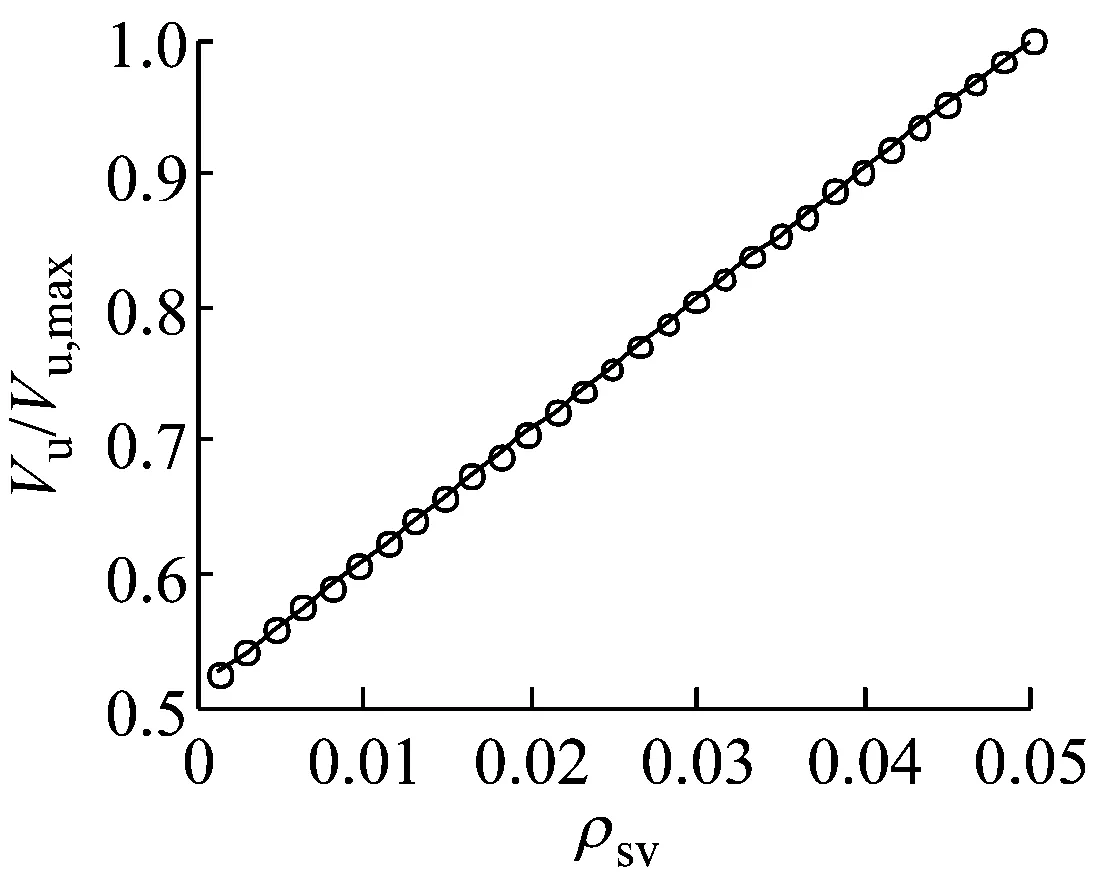
a 抗剪承载力与配箍率的关系曲线

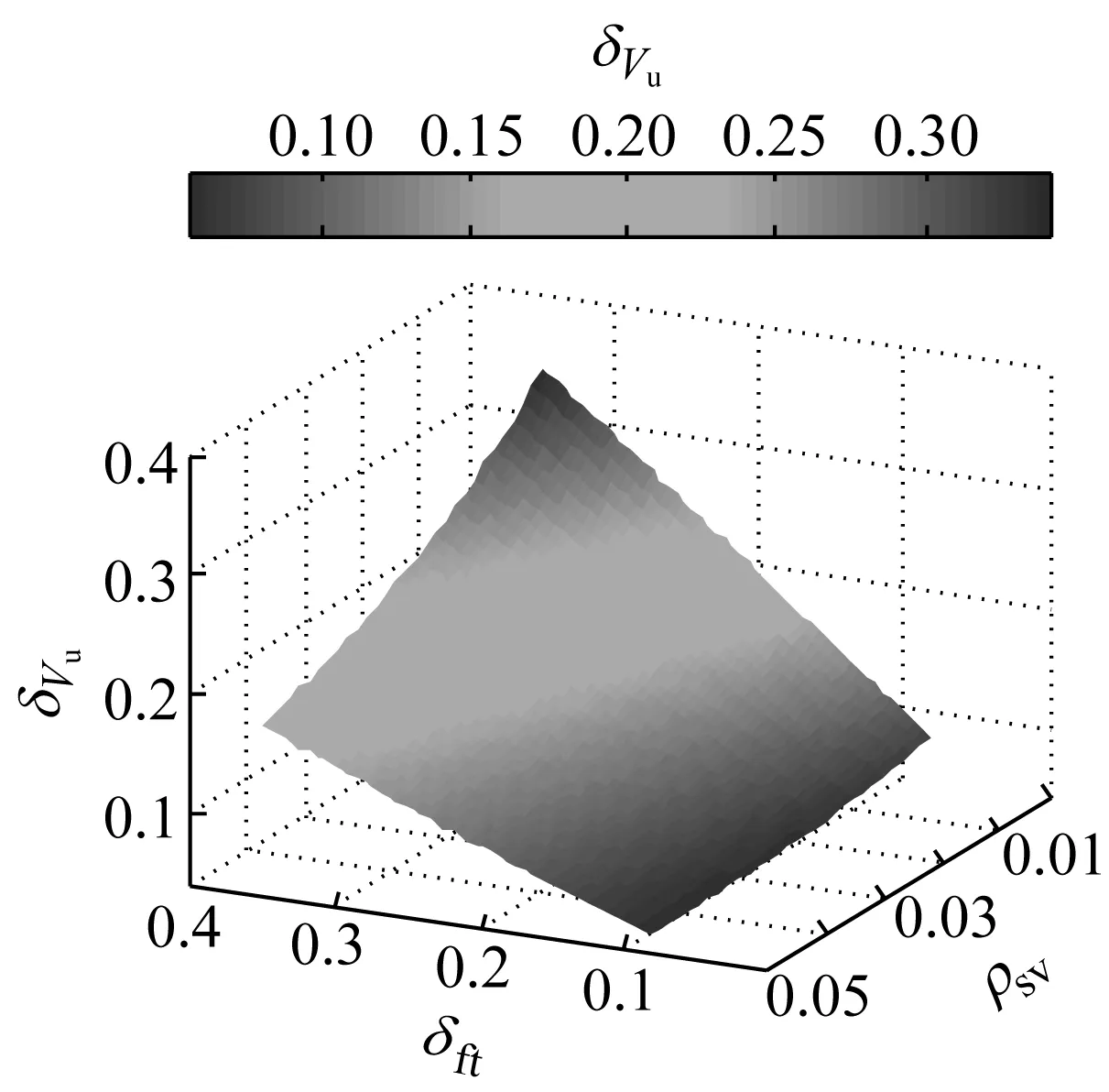
b 抗剪承载力变异系数图7　抗剪承载力统计参数Fig.7　Statistical parameters of shear capacity

由图7a可知，再生混凝土梁的受剪承载力随配箍率增长近似呈直线上升.图7b显示，在配箍率较小时，再生混凝土的抗拉强度变异性对梁的受剪承载力的变异性影响很大，这与再生混凝土梁受弯时是相反的.随着配箍率增长，这种影响呈下降趋势，尤其是在再生混凝土抗拉强度变异系数很高时，下降趋势更明显.这主要是由于箍筋对受剪承载力的贡献随配箍率的增长而增长，同时箍筋强度的变异系数较再生混凝土要低，最终导致受剪承载力的变异系数降低.

3　结论

(1) 再生混凝土梁受弯时，最小配筋率随再生混凝土强度的变异系数增长而缓慢增长.当变异系数为0.35时，再生混凝土梁的最小配筋率相比较普通混凝土梁仅增加约0.1%.随着配筋率的增长，再生混凝土强度变异系数对梁抗弯承载力的变异系数影响增大.

(2) 再生混凝土强度的变异系数对再生混凝土梁受剪(考虑均布荷载作用)时的最小配箍率影响显著，对于C30混凝土，当变异系数为0.2时，再生混凝土梁的最小配箍率为0.17%，相比较普通混凝土梁增加约32.0%.这主要是由于在最小配箍率情况下，梁中的剪力主要由混凝土承担，再生混凝土抗拉强度变异性对受剪承载力变异性影响很大，导致可靠指标降低，需要增加箍筋来保持可靠指标不变.

(3) 对于再生混凝土梁受弯，由于钢筋较混凝土对受弯承载力的贡献更大，钢筋的存在能够限制再生混凝土抗压强度的高变异性对抗力变异性的影响，再生混凝土更适用于受弯构件.

(4) 保持再生混凝土与普通混凝土强度均值一致，再生混凝土梁受弯或受剪时，通过合理提高再生混凝土梁的配筋率或配箍率，都可以保证再生混凝土梁达到现行规范规定的目标可靠指标.

(5) 本文仅讨论了再生混凝土梁受弯时的最小配筋率和受剪时的最小配箍率，有关再生混凝土的材料分项系数，值得今后进一步研究.

[1]肖建庄. 再生混凝土 [M]. 北京：中国建筑工业出版社, 2008.

XIAO Jianzhuang. Recycled concrete [M]. Beijing: China Architecture & Building Press, 2008.

[2]Gómez-Soberón J M V. Porosity of recycled concrete with substitution of recycled concrete aggregate [J]. Cement and Concrete Research, 2002, 32(8): 1301.

[3]屈文俊, 方瑾, 周国全. 混凝土受弯构件受拉钢筋最小配筋率 [J]. 建筑科学与工程学报, 2011, 28(1): 6.

QU Wenjun, FANG Jin, ZHOU Guoquan. Minimum reinforcement ratio of tensile reinforcement for concrete flexural members [J]. Journal of Architecture and Civil Engineering, 2011, 28(1): 6.

[4]何政, 李光. 基于可靠度的 FRP 筋材料分项系数的确定 [J]. 工程力学, 2008, 25(9): 214.

HE Zheng, LI Guang. Reliability-based calibration of material partial factor of fiber reinforced polymer (FRP) rod [J]. Engineering Mechanics, 2008, 25(9): 214.

[5]Breccolotti M, Materazzi A L. Structural reliability of eccentrically-loaded sections in RC columns made of recycled aggregate concrete [J]. Engineering Structures, 2010, 32(11): 3704.

[7]Ulloa V A, Garcia-Taengua E, Pelufo M, et al. New views on effect of recycled aggregates on concrete compressive strength [J]. ACI Materials Journal, 2013, 110(6): 687.

[8]肖建庄, 雷斌, 袁飚. 不同来源再生混凝土抗压强度分布特征研究 [J]. 建筑结构学报, 2008, 29(5): 94.

XIAO Jianzhuang, LEI Bin, YUAN Biao. Compressive strength distribution of recycled aggregate concrete derived from different origins [J]. Journal of Building Structures, 2008, 29(5): 94.

[9]中华人民共和国住房和城乡建设部. JGJ 55—2011普通混凝土配合比设计规程 [S]. 北京：中国建筑工业出版社，2011.

[10]常乐, 王淑丽,王紫轩. 钢筋强度标准值及其分项系数的校准研究 [J]. 工程质量, 2012, 30(4): 61.

CHANG Le, WANG Shuli, WANG Zixuan. Calibration of the steel strength standard value and the partial coefficient [J]. Construction Quality, 2012, 30(4): 61.

[11]中华人民共和国住房和城乡建设部. GB 50153—2008工程结构可靠性设计统一标准 [S]. 北京：中国建筑工业出版社，2008.

Reliability-based Study on Minimum Reinforcement Ratio of Recycled Aggregate Concrete Beams

ZHANG Kaijian1, XIAO Jianzhuang1, 2, DING Tao1, HU Bo1

(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

In order to investigate the influence of recycled aggregate concrete (RAC) strength variation on the minimum reinforcement and stirrup ratios of RAC beams, this paper analyzed and compared the ratios of RAC and natural aggregate concrete (NAC) beams subjected to bending moment and shear force with the same target reliability index. The results indicate that the RAC strength variation has limited influence on the flexural capacity variation with the existence of reinforcements. As a result, the minimum reinforcement ratio almost does not increase when the beams are subjected to moment. As for the beams subjected to shear force, when the coefficient of variation of RAC tensile strength is 0.2, the minimum stirrup ratio of RAC beam is 0.17% and increases about 32.0% compared with NAC (grade C30) beam. The reliability indexes of RAC and NAC beams can be equal by increasing the reinforcement and stirrup ratios reasonably.

recycled aggregate concrete (RAC); beam; strength variation; minimum reinforcement ratio; minimum stirrup ratio; reliability index

2015-03-18

国家自然科学基金(51325802)

张凯建(1989—)，男，博士生，主要研究方向为再生混凝土结构. E-mail:2013zkj@tongji.edu.cn

肖建庄(1968—)，男，教授，博士生导师，工学博士，主要研究方向为再生混凝土. E-mail: jzx@tongji.edu.cn

TU375.1;TU528

A