考虑剪胀效应的混凝土动态球形空腔膨胀理论

张欣欣,闫雷,武海军,黄风雷

(1.北京理工大学爆炸科学与技术国家重点实验室,北京100081; 2.山东特种工业集团有限公司,山东淄博255201)

考虑剪胀效应的混凝土动态球形空腔膨胀理论

张欣欣1,闫雷2,武海军1,黄风雷1

(1.北京理工大学爆炸科学与技术国家重点实验室,北京100081; 2.山东特种工业集团有限公司,山东淄博255201)

在考虑混凝土的压缩和扩容特性条件下,建立了动态球形空腔膨胀理论,其中完整的靶体响应为密实区-扩容区-开裂区-弹性区,在扩容区采用扩容方程。基于上述理论得到了空腔表面应力与膨胀速度的表达式,使用侵彻方程计算不同工况的侵彻深度并与试验值作对比,同时对混凝土强度参数和压缩系数对弹体侵彻深度的影响规律进行研究。结果表明:该模型可以较好预测侵彻深度,具有一定的合理性;混凝土强度参数中压力硬化系数对侵彻深度的影响较大,随着弹体初速度增大应考虑混凝土材料的剪切饱和性质;随着压缩系数不断减小,混凝土材料由压缩转为膨胀状态,导致空腔表面应力增加,侵彻深度降低。

兵器科学与技术;混凝土;球形空腔膨胀理论;剪胀效应;侵彻

DOI:10.3969/j.issn.1000-1093.2016.01.007

0 引言

空腔膨胀理论是一种最基本的理论方法用来求解侵彻过程中弹体表面的受力情况。空腔膨胀理论最初由Bishop等[1]提出,他们于1945年建立了准静态空腔膨胀理论,用于研究锥形头部冲杆的受力。之后Goodier[2]最先把该理论应用于弹体侵彻上,通过一系列合理的假设,对球形空腔膨胀理论进行修改,得到了球形弹体在靶体中总阻力,再由运动方程得到了侵彻规律。Forrestal等[3]对可压缩弹塑性靶体进行球形空腔膨胀分析,得到了空腔表面应力与膨胀速度之间的关系,其中靶体采用线性静水压力-体积应变关系以及Tresca屈服准则,靶体响应为塑性区-弹性区。Forrestal等[4]采用线性静水压力-体积应变关系及带拉伸破坏的Mohr-Coulomb屈服准则对混凝土的球形空腔膨胀进行研究,得到了可压缩及不可压缩情况下空腔表面应力和膨胀速度的关系式。Satapathy[5]在文献[3-4,6-7]的研究基础之上采用Mohr-Coulomb屈服准则对陶瓷材料进行了球形空腔膨胀分析。李志康等[8]在前人研究成果的基础上,基于简化后的Holmguist-Johnson-Cook三段式静水压力-体积应变关系以及Mohr-Coulomb Tresca-limit屈服准则建立了比较完备的空腔膨胀模型。

上述文献中描述混凝土的静水压力和体积应变的方程均为压缩方程,而在混凝土试件的三轴压缩试验中可观察到混凝土的剪切扩容现象,即随着静水压力的增大,混凝土体积呈现膨胀状态。

Thomas等[9]分别采用不同的加载路径(静水压加载,三轴加载,比例加载)对混凝土实际变形进行试验,由试验结果可得,混凝土材料在静水压加载情况下,所受各向应力均相等,材料一直呈现压缩状态,但在三轴加载时,随着偏应力的出现并逐渐增大混凝土材料会由压缩转向膨胀状态。Xuan等[10]分别对不同饱和度的混凝土进行三轴试验,结果显示,材料在偏应力的作用下会出现剪胀现象,并且压缩-扩容的转折应力点和材料的屈服极限相近。He等[11]和Guo等[12]分别建立了考虑混凝土剪胀效应的动态球形和柱形空腔膨胀模型,该模型采用弹性-开裂-密实分区,并且在密实区引入扩容方程,使用该模型计算得到的侵彻深度值和试验结果较符合,表明模型具有一定合理性。

由文献[13-14]可得,在较高静水压加载下,混凝土靶体扩容特性消失,只呈现压缩状态。因此本文在上述研究的基础上,同时考虑混凝土材料的压缩和扩容特性,建立了动态球形空腔膨胀模型,将靶体分为密实区、扩容区、开裂区以及弹性区,在扩容区采用扩容方程,在密实区采用压缩方程,得到空腔表面径向应力和膨胀速度的拟合表达式,利用侵彻公式对卵形弹体的侵彻深度进行计算并与试验值作对比,同时研究混凝土强度参数及压缩系数对侵彻深度的影响规律。

1 球形空腔膨胀理论

本文在前人研究的基础上,同时考虑混凝土的压缩及扩容特性,形成新的空腔膨胀理论。该模型具有弹性区、开裂区、扩容区以及密实区,空腔膨胀分区形式如图1所示。

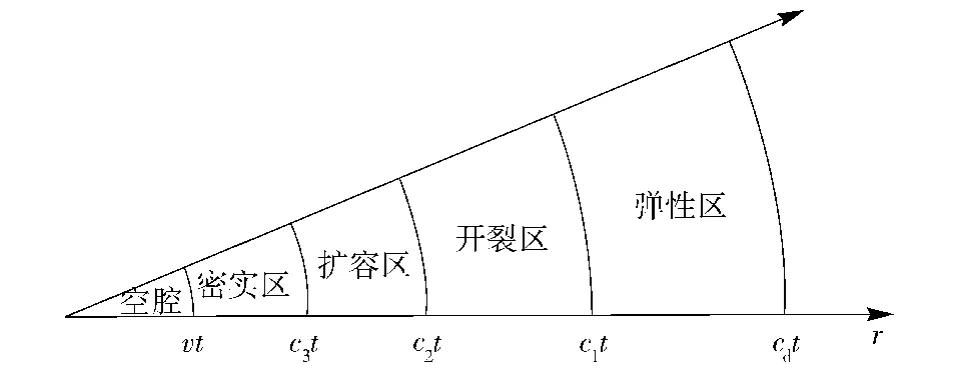
图1 动态球形空腔膨胀分区示意图Fig.1 The regions of dynamic spherical cavity expansion

在Euler坐标系下,球形空腔膨胀的质量守恒和动量守恒方程分别为

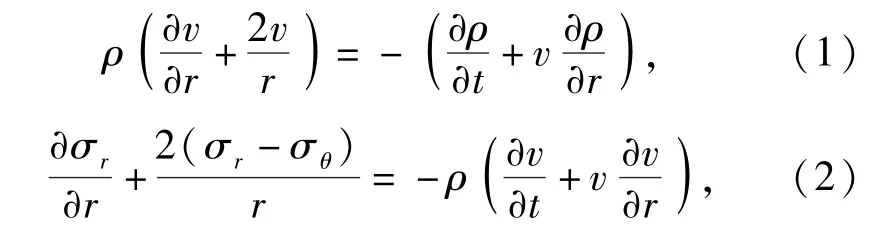
式中:ρ表示混凝土材料密度(混凝土为可压缩材料,密度可变);v表示质点速度;r表示径向坐标;t为时间。

在动态球形空腔膨胀的过程中,各个响应区域的交界面上需要满足Hugoniot间断条件。质量和动量守恒形式的Hugoniot间断条件为

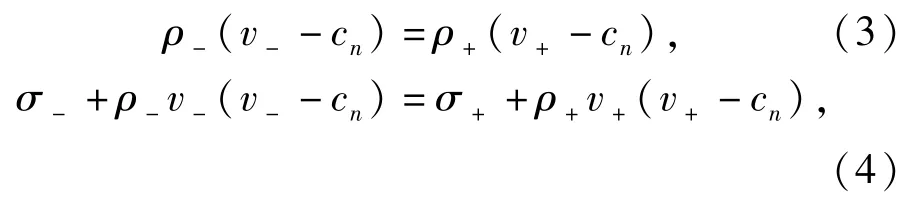
式中:ρ+、ρ-分别为波前、波后介质的密度;v+、v-分别为波前、波后介质的质点速度;cn为波阵面速度; σ+、σ-分别为波前、波后介质中的正应力。

1.1 弹性区

弹性区的混凝土材料可以用经典的Hooke定律描述,球坐标下径向和周向应力为

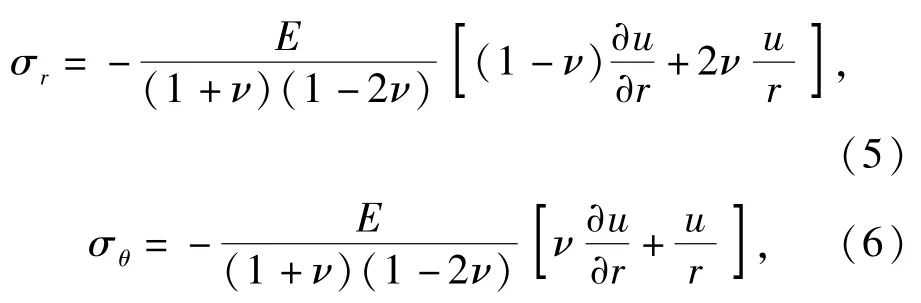
式中:E表示混凝土的杨氏模量;ν表示泊松比;u表示质点位移。将上面两式代入到方程(2)式中可得

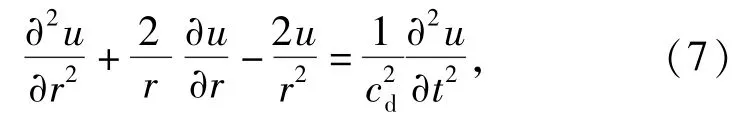
式中:cd是混凝土的弹性体积波波速,

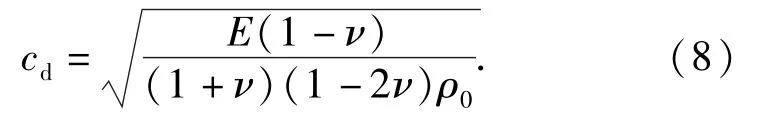
引入相似变换:

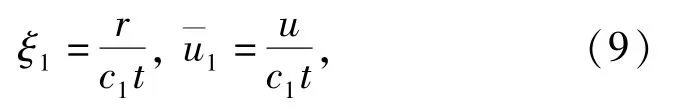
式中:c1表示弹性区与开裂区的界面传播速度。则(7)式可由(9)式变化为常微分方程

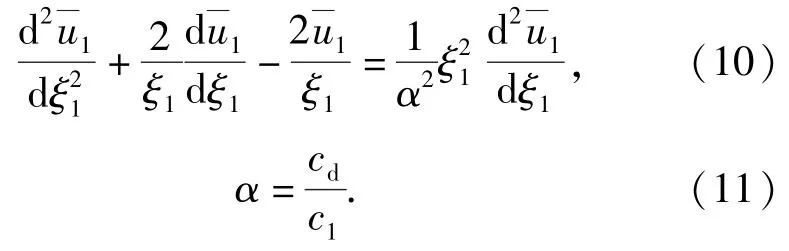
解上述常微分方程可得通解形式:

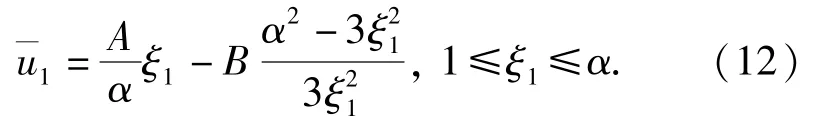
已知弹性波阵面处的质点位移为0,且弹性区与开裂区界面处的周向应力等于混凝土材料的抗拉强度-f,因此有

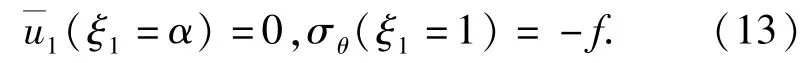
将边界条件(13)式代入(12)式和(6)式可解得

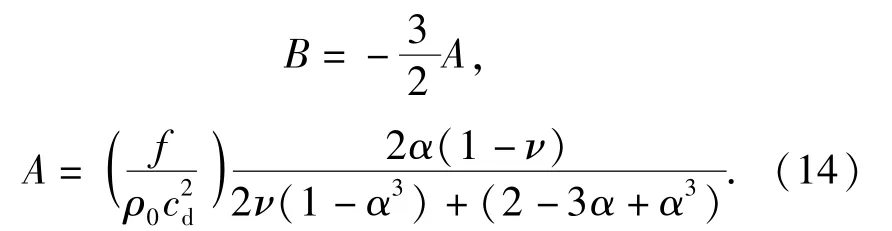
1.2 开裂区

在开裂区,混凝土材料处于周向应力为0的状态,可以认为混凝土材料在径向处于无围压压缩的弹性状态。则(2)式变为

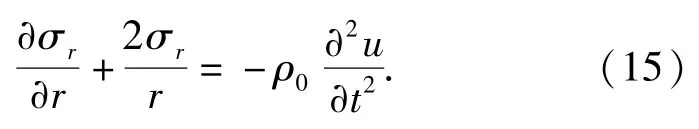
由于材料处于无围压弹性状态,径向应力可以表示为

代入(15)式可得到偏微分方程

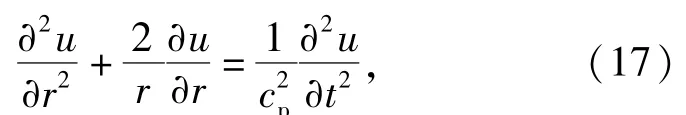
引入相似变换

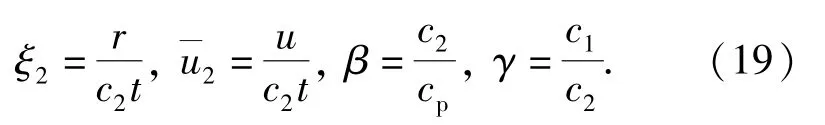
将(17)式变为常微分方程

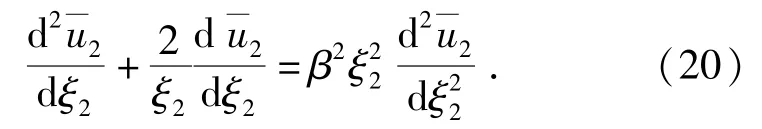
方程(20)式的通解为

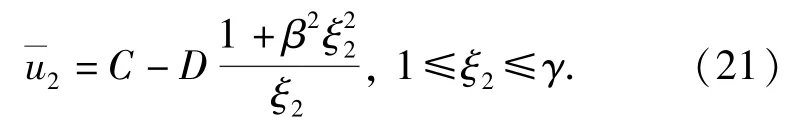
弹性区与开裂区在界面处有位移连续条件,无量纲位移关系如下:

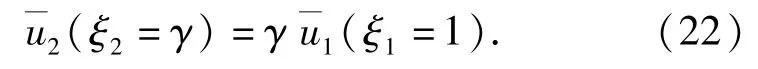
径向应力在开裂区与扩容区的界面处应当等于混凝土材料单轴抗压强度f＇c:

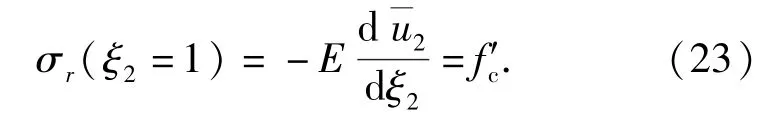
将边界条件(23)式代入到(21)式中可得

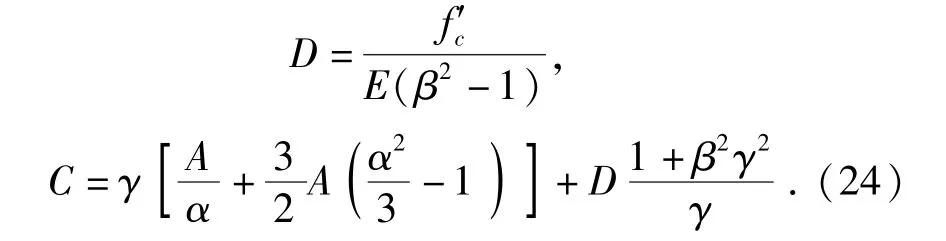
由(5)式,(12)式和(14)式可求得弹性区与开裂区界面处,位于弹性区一侧的质点速度、径向应力以及体积应变:

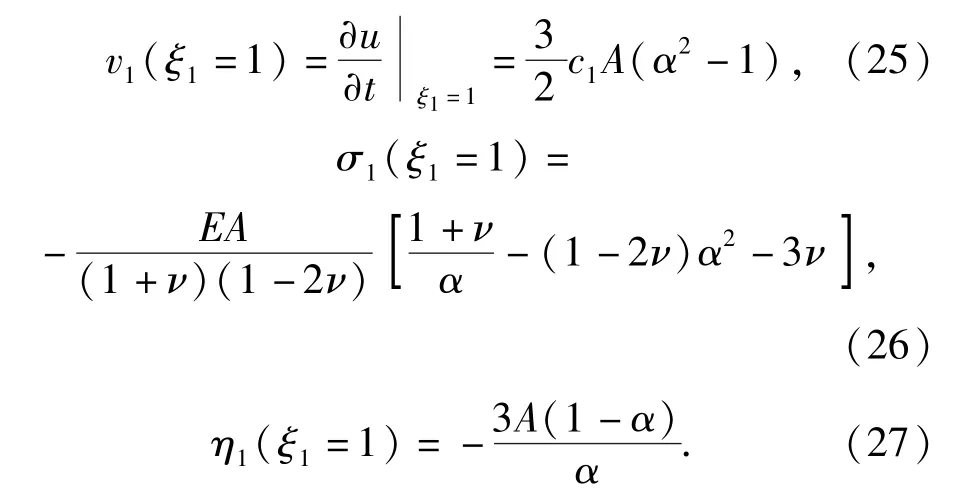
同理,由(16)式,(21)式和(24)式可以求得该界面开裂区一侧的径向应力与体积应变:

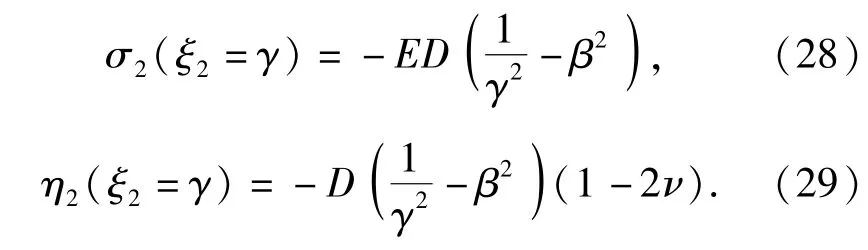
将上述界面处物理量代入弹性区与开裂区界面处的Hugoniot跳跃条件,可以得到如下等式

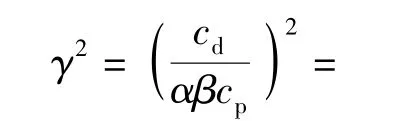
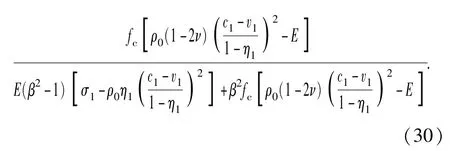
1.3 扩容区

在扩容区使用扩容方程[11,13]如下所示:

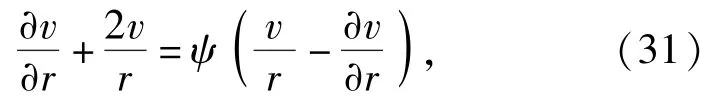
在扩容区材料满足Mohr-Coulomb屈服准则:

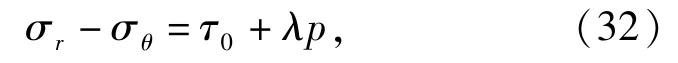
式中:τ0为混凝土的粘聚强度;λ为硬化系数;p=为静水压力。

积分(31)式,并且取边界条件v(c2t,t)=v3,可得

式中:v3为扩容区和开裂区交界处扩容区一侧的质点速度;k为压缩系数,由文献[13]可得,当k=2时,材料处于不可压缩状态;当k＞2时,材料处于压缩状态;当k＜2时,材料处于膨胀状态。因此在扩容区有k＜2.

将(33)式代入到(1)式中,可得

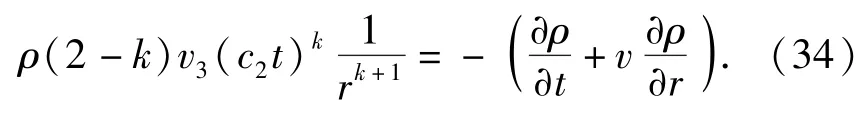
在扩容区有相似变换:

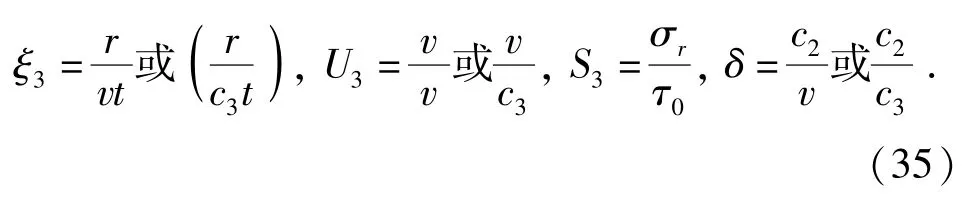
由(34)式、(35)式联立可得

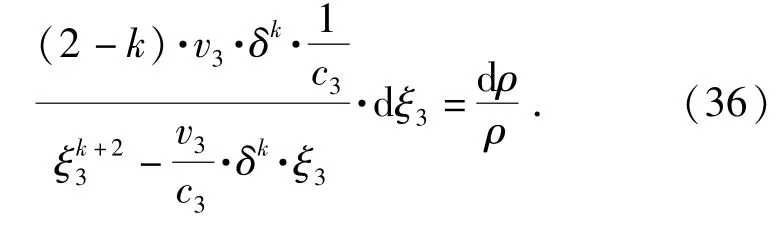
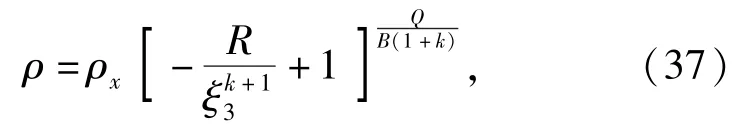
式中:ρχ为积分常数。当ξ3=δ时,ρ=ρ3;当ξ3=1时,ρ=ρ4.将此条件代入到(37)式中可得

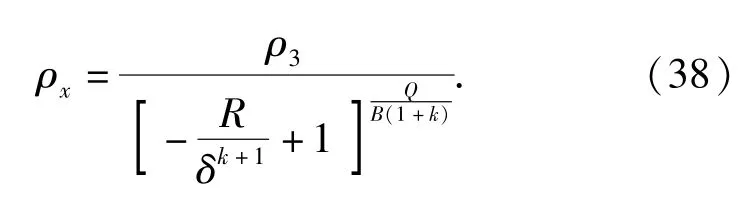
由(33)式可得

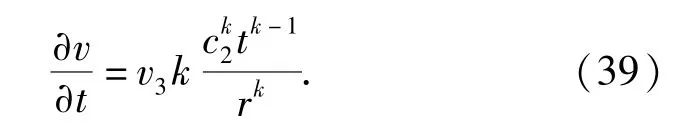
将(32)式和(39)式代入到(2)式中经化简可得

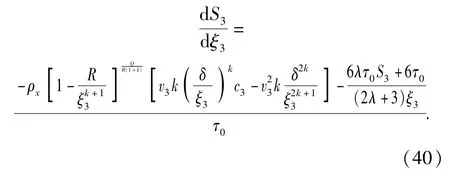
由(16)式,(21)式和(24)式计算可得,开裂区和扩容区交界处开裂区一侧的质点速度、径向应力、体积应变及密度分别为

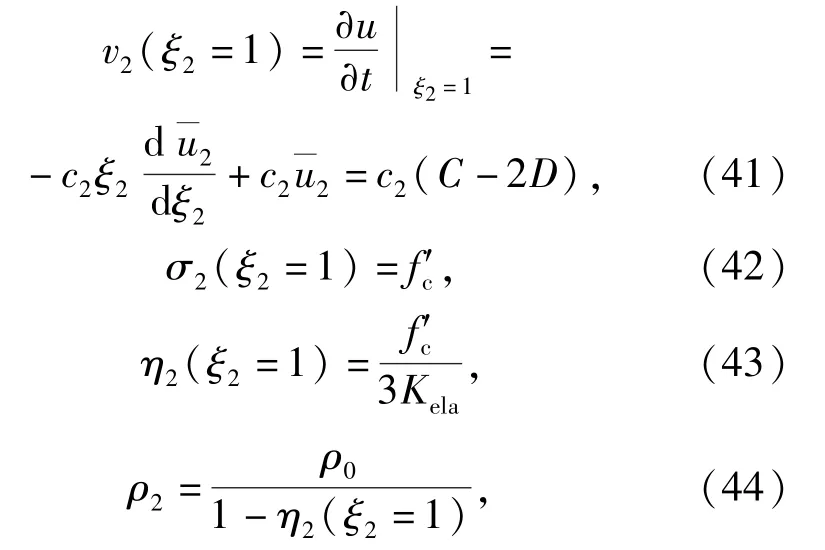
式中:ρ0为混凝土初始密度。

由Hugoniot间断条件可得,开裂区和扩容区交界处扩容区一侧的质点速度和径向应力分别为

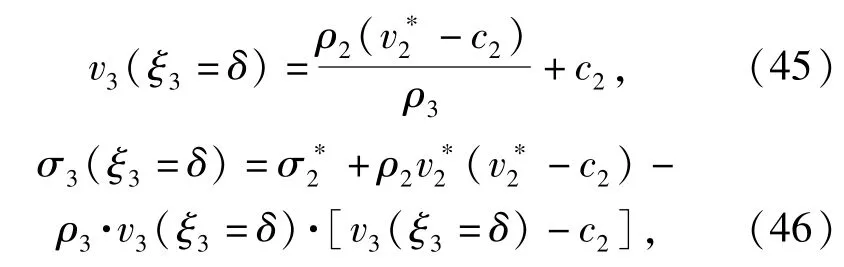
式中:v*2=v2(ξ2=1);σ*2=σ2(ξ2=1).

1.4 密实区

在密实区采用Tresca屈服准则:

在密实区的压缩方程为

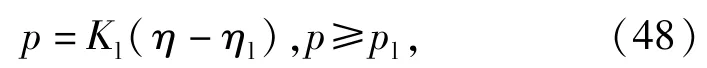
式中:η为体积应变;Kl为密实段体积模量;pl为密实区初始压力;ηl为密实区初始体积应变。

由(47)式和(48)式联立,并引入相似变换:

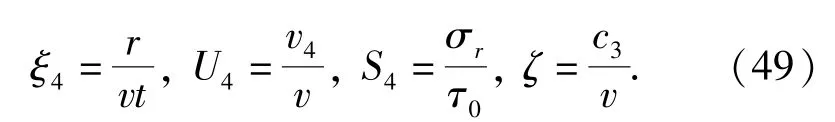
则质量守恒方程(1)式和动量守恒方程(2)式可以变换为

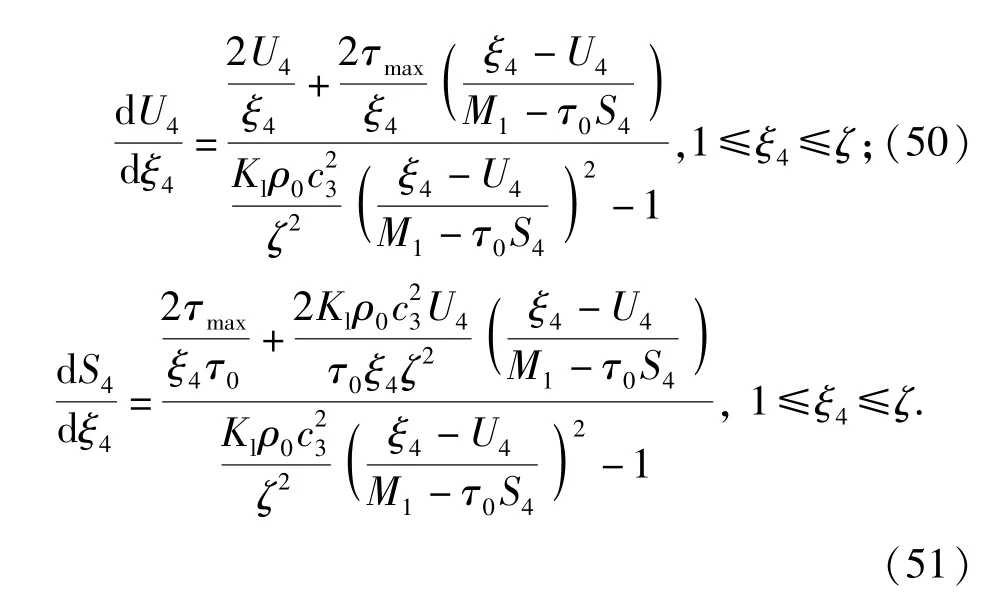
式中:

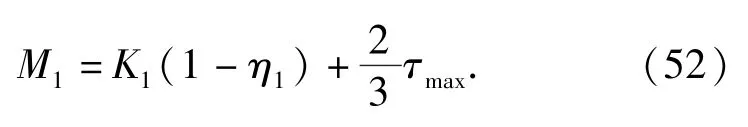
由Hugoniot间断条件可得,扩容区和密实区交界处密实区一侧的质点速度和径向应力分别为

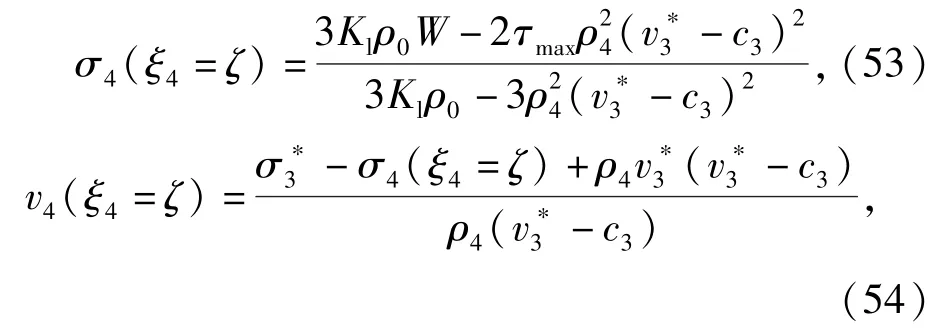
式中:

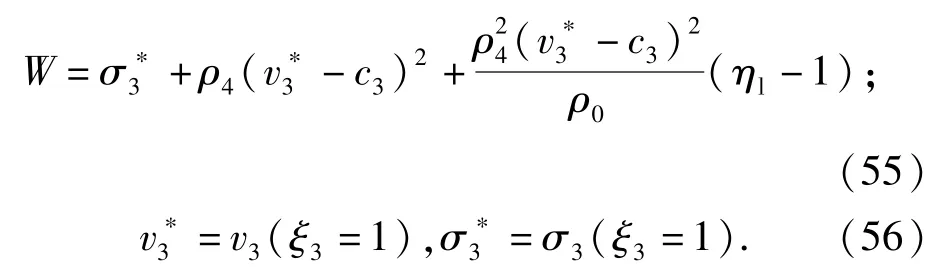
由于没有后续的区域出现,ξ4=1仅代表空腔边界,所以边界条件为

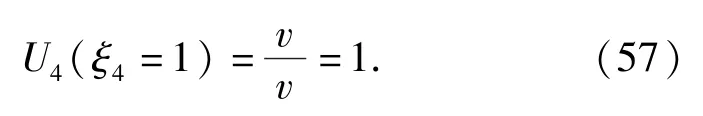
2 空腔表面径向应力及界面速度计算结果

由文献[14]可得,对于混凝土材料,扩容区内压缩系数取值范围为1.24＜k＜2,根据文献[11,13]本文计算k取1.8.对于无约束抗压强度为48 MPa的混凝土,采用文献[15]中所提出的混凝土本构模型参数,并根据本文推导的空腔膨胀理论公式,运用Matlab程序对空腔膨胀过程中的径向应力和膨胀速度的关系及区域界面速度进行数值计算,计算结果如图2和图3所示。

由图2可得,空腔表面径向应力随着压缩系数k值的减小而增大,当k值逐渐减小时,混凝土材料由压缩转为膨胀状态,因此空腔表面径向应力增大。

由图3可得,当空腔边界膨胀速度较低时,靶体响应为弹性-开裂-扩容分区,随着空腔边界膨胀速度逐渐增大,密实区出现,开裂区消失。

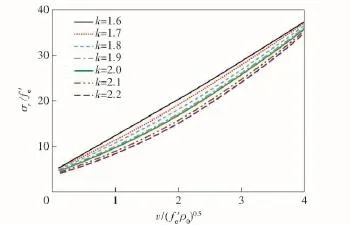
图2 无量纲空腔膨胀边界径向应力与膨胀速度计算结果Fig.2 The relation between dimensionless cavity stress and expansion speed

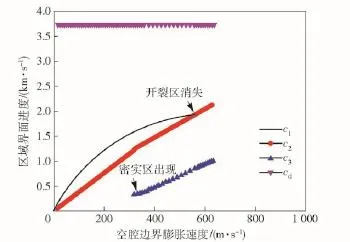
图3 动态球形空腔膨胀区域界面传播速度(k=1.8)Fig.3 The speed of region boundary in spherical cavity expansion(k=1.8)

采用二次多项式对图2中曲线进行拟合可得如下函数关系:

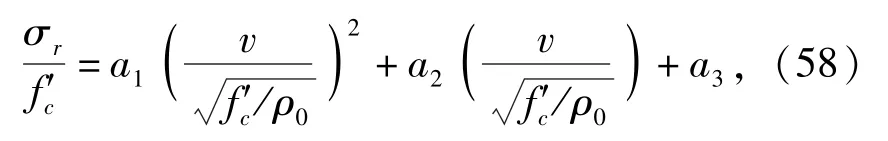
式中:a1,a2,a3为拟合参数。

3 刚性弹体侵彻计算等式的验证比较

图4为本文及文献[11]中理论计算值和文献[16]中试验数据对比,其中弹体质量为13 kg,直径为0.076 2 m,靶体参数参考文献[15]。由图4可得,两种理论计算结果较为接近,并均与试验数据吻合较好。对于头部卵形系数CRH=6的弹体,使用本文理论模型计算得到的侵彻深度更加接近试验值。

图5和图6分别为本文及文献[11]中理论计算值和文献[17-18]中试验数据对比,图5中弹体质量为0.9 kg,直径为0.269 m,图6中弹体质量分别为0.48 kg和1.60 kg,直径为0.203 m和0.305 m,弹体头部卵形系数CRH=3.0.靶体参数参考文献[15]。由图5、图6可得,两种理论计算结果均与试验数据吻合较好。当弹体初速较小时,靶体处于扩容状态,因此两种计算模型所得结果较接近。对于无约束抗压强度分别为36.2 MPa和51.0 MPa的混凝土靶体,随着弹体初速增大,本文理论计算值明显大于文献[11]中计算值,原因在于高速工况下靶体出现密实区,混凝土呈现压缩状态,从而导致空腔表面应力相比扩容状态有所下降,而强度为96.7 MPa混凝土的侵彻深度计算结果则较为接近,表明混凝土无约束抗压强度对侵彻深度计算有较大影响,和文献[11,19-20]中结果类似。相比文献[11]中理论模型,本文模型可以较好描述高速情况下混凝土侵彻机理,具有更广的适用性。

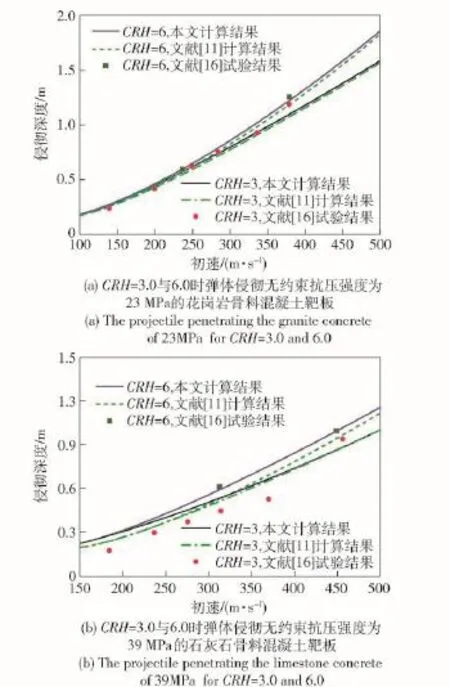
图4 侵彻深度等式计算结果与试验数据[16](k=1.8)Fig.4 The comparison of calculated and experimental penetration depths[16](k=1.8)

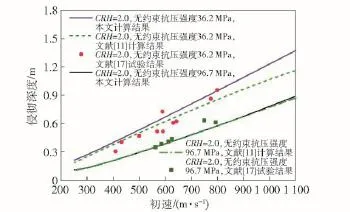
图5 侵彻深度等式计算结果与试验数据[17](k=1.8)Fig.5 The comparison of calculated and experimental penetration depths[17](k=1.8)

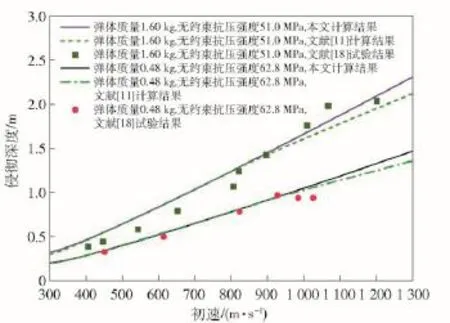
图6 侵彻深度等式计算结果与试验数据[18](k=1.8)Fig.6 The comparison of calculated and experimental penetration depths[18](k=1.8)

4 混凝土材料强度参数及压缩系数对刚性弹体侵彻深度的影响

以文献[15]中无约束抗压强度为48 MPa混凝土模型参数为参考,通过对混凝土强度参数和压缩系数分别取值来计算单个参量对弹体侵彻深度的影响规律,计算结果如图7所示。其中弹体长度为0.3 m,直径为0.03 m,弹体密度为7 850 kg/m3,头部卵形系数CRH=3.0.

由图7(a)～图7(c)可得,侵彻深度随着混凝土各强度参数的增大而减小。压力硬化系数和粘聚强度在整个速度范围内对侵彻深度均有影响,并且压力硬化系数影响较为显著。最大剪切强度在弹体初速较低时影响不大,随着初速增大,靶体出现密实区,应考虑混凝土材料的剪切饱和性质,与文献[5,8]中结论一致。

由图7(d)可得,侵彻深度随着压缩系数减小而减小,即随着压缩系数的减小,混凝土材料由压缩转为膨胀状态,增加空腔表面应力,从而减少侵彻深度。

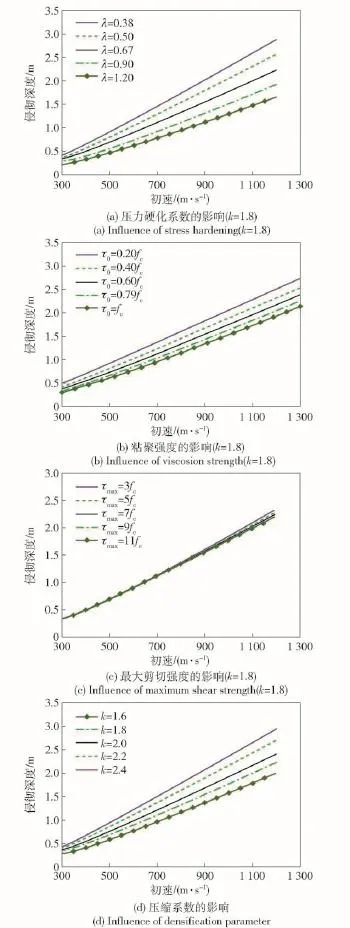
图7 混凝土材料强度参数及压缩系数对侵彻深度的影响Fig.7 The influences of concrete strength and densification parameter on the depth of penetration

5 结论

本文同时考虑混凝土的压缩和扩容特性,建立了动态球形空腔膨胀理论,其中完整的靶体响应为密实区-扩容区-开裂区-弹性区,基于上述理论得到了空腔表面应力与膨胀速度的表达式,使用侵彻方程计算不同工况的侵彻深度并与试验值作对比,最后对混凝土强度参数和压缩系数对弹体侵彻深度的影响规律进行研究。可得如下结论:

1)由计算结果可得,本文所提模型可以较好预测侵彻深度,具有一定的合理性。

2)混凝土强度参数中压力硬化系数对侵彻深度的影响较大,最大剪切强度在弹体初速较低时影响较小,随着弹体初速增大应考虑混凝土材料的剪切饱和性质。

3)随着k值的不断减小,混凝土材料由压缩转为膨胀状态,导致空腔表面应力增加,侵彻深度降低。

References)

[1]Bishop R F,Hill R,Mott N F.The theory of indentation and hardness[J].Proceedings of the Physical Society,1945,57(3): 147-155.

[2]Goodier J N.On the mechanics of indentation and cratering in solid targets of strain-hardening metal by impact of hard and soft spheres[C]//Proceedings of the 7th Symposium on Hypervelocity Impact.Tampa,FL,US:AIAA,1965:215-219.

[3]Forestal M J,Luk V K.Dynamic spherical cavity-expansion in a compressible elastic-plastic solid[J].Journal of Applied Mechanics,1988,55(2):275-279.

[4]Forrestal M J,Tzou D Y.A spherical cavity-expansion penetration model for concrete targets[J].International Journal of Solids Structure,1997,34(31/32):4127-4146.

[5]Satapathy S.Dynamic spherical cavity expansion in brittle ceramics[J].International Journal of Solids Structure,2001,38(32/33):5833-5845.

[6]Longcope D B,Forrestal M J.Penetration of targets described by a Mohr-Coulomb failure criterion with a tension cutoff[J].Applied Mechanics,1983,50(2):327-333.

[7]Forrestal M J,Luk V K.Penetration into soil targets[J].International Journal of Impact Engineering,1992,12(3):427-444.

[8]李志康,黄风雷.混凝土材料的动态空腔膨胀理论[J].爆炸与冲击,2009,29(1):95-100.LI Zhi-kang,HUANG Feng-lei.A dynamic spherical cavity-expansion theory for concrete materials[J].Explosion and Shock Waves,2009,29(1):95-100.(in Chinese)

[9]Thomas G,Yann M,Laurent D.Triaxial behaviour of concrete under high stresses:influence of the loading path on compaction and limit states[J].Cement and Concrete Research,2008,38(3):403-412.

[10]Vua X H,M Y,Daudevillea L,et al.Experimental analysis of concrete behavior under high confinement:effect of the saturation ratio[J].International Journal of Solids and Structures,2009,46(5):1105-1120.

[11]He T,Wen H M,Guo X J.A spherical cavity expansion model for penetration of ogival-nosed projectiles into concrete targets with shear-dilatancy[J].Acta Mechanica Sinica,2011,27(6): 1001-1012.

[12]Guo X J,He T,Wen H M.Cylindrical cavity expansion penetration model for concrete targets with shear dilatancy[J].Journal of Engineering Mechanics,2013,139(9):1260-1267.

[13]Nikolaevskij V N.Mechanics of porous and fractured media [M].Singapore:World Scientific,1990.

[14]Vermeer P A,de Borst R.Non-associated plasticity for soils,concrete and rock[J].HERON,1984,29(3):1-64.

[15]Holmquist T J,Johnson G R,Cook W H.A computational constitutive model for concrete subjected to large strains,high strain rates,and high pressures[C]//14th International Symposium on Ballistics.Quèbec,Canada:ADPA,1993.

[16]Forrestal M J,Frew D J,Hickerson J P,et al.Penetration of concrete targets with deceleration-time measurements[J].International Journalof Impact Engineering,2003,28(5):479-497.

[17]Forrestal M J,Altman B S,Cargile J D,et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J].International Journal of Impact Engineering,1992,15(4):395-405.

[18]Forrestal M J,Frew D J,Hanchak S J,et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].International Journal of Impact Engineering,1996,18(5): 465-476.

[19]Wen H M,Xian Y X.A unified approach for concrete impact [J].International Journal of Impact Engineering,2015,77: 86-96.

[20]Wen H M,Yang Y.A note on the deep penetration of projectiles into concrete[J].International Journal of Impact Engineering,2014,66:1-4.

A Note on the Dynamic Spherical Cavity Expansion of Concrete with Shear Dilatancy

ZHANG Xin-xin1,YAN Lei2,WU Hai-jun1,HUANG Feng-lei1
(1.State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China; 2.Shandong Special Industry Group Co.Ltd,Zibo 255201,Shandong,China)

Considering the compression and dilatation of the concrete,a model of dynamic spherical cavity expansion is constructed,where the complete response of target is densification region-dilatation regioncrack region-elastic region,and the dilatant-kinematic relation is used for the dilatation region.The expression of cavity stress and expansion speed is obtained with the theory above,and the depths of penetration in different conditions are calculated.The effects of the concrete strength and dilatation on penetration depth are analyzed.The results indicate that the proposed model is reasonable to predict the depth of penetration;the stress hardening parameter has a great influence on the depth of penetration,and the shear saturation should be considered with the increase in the projectile volecity;with the decrease in the densification parameter,the condition of the concrete turns into dilatation from compression,resulting in the increase in cavity stress and the decrease in depth of penetration.

ordnance science and technology;concrete;dynamic spherical cavity expansion;shear-dilatancy;penetration

O385

A

1000-1093(2016)01-0042-08

2015-06-24

国家自然科学基金项目(11390362、11572048);国防基础科研项目(B1020132071)

张欣欣(1987—),男,博士研究生。E-mail:xxwade2020@163.com;武海军(1974—),男,教授,博士生导师。E-mail:wuhj@bit.edu.cn