基于蒙特卡洛仿真和遗传算法的车辆装备保障运输网络优化

陈春良,齐鸥,魏兆磊,刘彦

(装甲兵工程学院技术保障工程系,北京100072)

基于蒙特卡洛仿真和遗传算法的车辆装备保障运输网络优化

陈春良,齐鸥,魏兆磊,刘彦

(装甲兵工程学院技术保障工程系,北京100072)

车辆装备保障运输网络优化是影响非战争军事行动任务效果的关键环节。传统方法描述随机且不连续装备保障需求的能力弱,应用于非战争军事行动车辆装备保障运输网络优化方面,会导致结果不稳定。为解决这些问题,提出了基于蒙特卡洛仿真和遗传算法的车辆装备运输网络优化模型。结合非战争军事行动特点,利用边界条件设定,保障资源调度优化函数及保障资源约束条件设置,构建了车辆装备保障运输网络优化模型;采用遗传算法,在路网和运输路径两个层次对车辆装备保障运输网络进行寻优,进一步提高了运算结果的稳定性。通过残差分析验证了该模型的有效性。

兵器科学与技术;蒙特卡洛仿真;遗传算法;车辆装备保障;运输网络优化

DOI:10.3969/j.issn.1000-1093.2016.01.018

0 引言

运输网络优化是物资调配优化的重要环节,该环节通过开辟或修复部分受损的道路,达到减少非必要运输时间的目的,是提高物资装备调配效率的重要手段[1]。

非战争军事行动爆发突然,时间和地域不确定性强,为了节省成本,平时存储装备较少,灾害爆发时临时筹措大量的车辆装备,是非战争军事行动保障装备的主体[2]。车辆装备具有以下特点[3]:1)装备多属临时征集的建制外装备,在恶劣自然条件下耗损规律未知;2)任务前期耗损强度大,保障压力大;任务后期耗损量急剧降低,行动后期装备动用量小;3)自然环境复杂多变,保障需求随机不连续。

车辆装备作为遂行非战争军事行动的主体装备,其运输网络效能高低对于非战争军事行动任务的遂行至关重要,车辆装备保障运输网络优化涉及保障人员、装备和指挥关系的协调,是一个复杂问题[4-5]。车辆装备型号不统一,平战管理差异大,给装备保障带来了很大压力,为了有效应对非战争军事行动任务,需要对装备保障系统进行优化,运输网络优化是装备保障系统优化的重要一环[6-7]。

国内外学者针对这一问题进行了大量研究。Ning等[8]针对轴-辐区域的运输问题,提出了以最大运输能力、单位运输成本和单位货物处理成本为优化目标的模糊交互规划模型,实现了始发站-枢纽站-目的地之间的运输优化问题,该模型仅能处理少数几个节点间的运输优化问题,随着运输节点的增加,该模型计算复杂度成级数增加,实用性差。周骞等[9]提出了基于畅通度的城市物流配送运输网络优化模型,该模型在网络畅通可靠度理论的基础上,给出了模型简化求解算法,大大拓展了节点处理能力,但该模型没有考虑到网络堵塞条件下道路的修复问题,不能处理野外道路堵塞-修复条件下的运输问题。文献[10]针对水路混合运输交通量分配问题,提出了基于标准网络平衡状态的交通量分配模型,借助时空拓展转换法和独特路段阻抗结构法,解决道路堵塞-修复条件下的运输问题,但该模型仅能使用于理想情况,对于背景复杂的运输网络实用性差。吴琼等[11]提出了基于列生成算法的集装箱班轮运输网络优化模型,该模型建立港口货物运量、船队运能和承运人船舶数量的混合整数规划模型,提高了算法的实用性,但该方法没有考虑到车辆装备型号多样,保障需求随机不连续的特点,直接应用于非战争军事行动领域,将会造成最优解搜索过程延长,稳定性不足,计算结果与实际偏差过大的问题。

为了解决该问题,以某基层部队遂行非战争军事行动车辆装备保障任务为研究对象,采用Anylogic软件对由非战争军事行动任务、军队人员、保障节点组成的系统进行分析,通过受损道路修复和最优路径选择,提高了保障资源配置效率,为车辆装备保障任务的遂行提供技术支持。

1 蒙特卡洛仿真和遗传算法

蒙特卡洛仿真是在不能得到变量精确分布或近似精确分布的条件下,利用统计学方法得到变量基本性质的一种方法。

考虑独立同分布随机变量χ1,χ2,…,χn,假设要检验F(·)=G(·,θ)是否成立,其中θ是未知参数,G(·)为已知函数。对这个检验的任何统计量,蒙特卡罗仿真就是从分布中独立产生参考数据χ＇1,χ＇2,…,χ＇n,计算相应统计量的特征值T(χ＇1,χ＇2,…,χ＇n)作为参考值。其中是θ的估计值,如果T的值小于显著水平α,说明假设成立,可以用该分布近似模拟未知变量分布,否则说明原假设不成立,拒绝原假设,同时对检验条件做调整。

记T(χ1,χ2,…,χn)=T0,T1,T2,…,Tm为由蒙特卡洛仿真得到的m个参考值,T的估计值为

式中:k是T0,T1,…,Tm大于或等于T0的个数。因此,给定显著水平α,如果,拒绝原假设。

蒙特卡洛仿真可以在变量分布未知且样本量较小的条件下,得到变量的近似模拟,实现变量性质的精确分析,适用于非战争军事行动爆发突然,先验数据少,且需求规律未知的情况。

遗传算法是模拟自然界生物进化过程的一类寻优算法,该方法根据实际优化需求,将变量进行编码,并在空间中生成多个进化个体,利用有限优化适应度函数,评估进化过程的优劣,利用解码算法将进化种群进行交叉、变异和重组,实现在复杂条件下的快速精确寻优。

遗传算法通过变量编码,避开了其他寻优算法难以处理的函数求导不连续问题,有效保证寻优结果的收敛,能够较好处理非战争军事行动中偶发事件引起的保障需求突变的情况。

2 蒙特卡洛仿真模型构建

设非战争军事行动任务爆发区域道路路线图为G=(V,A),V={v1,…,vn;vA,…,vm}为保障节点和资源需求节点集,v1～vn为保障节点,其余为资源需求节点。A={(i,j)|i≠j,i,j∈V}为路段矩阵。节点i与j之间的保障物资运输时间为tij,运输物资数量为Q;单次运输最大容量、行程为c、S;修复失效或开辟新路段l消耗物资数量为Rl.

节点i申请需求量由资源需求数量评估结果确定,实际需求中,各单位难以精确统计本单位物资需求数量,多会根据对单位总体实力的把握,给出一个近似值,该值具有一定的模糊性和随机性,为了降低物资需求不精确性对车辆保障的影响,采用先验概率模糊函数对其进行处理,将该单位上报物资需求数量i设为随机模糊变量ξi,则

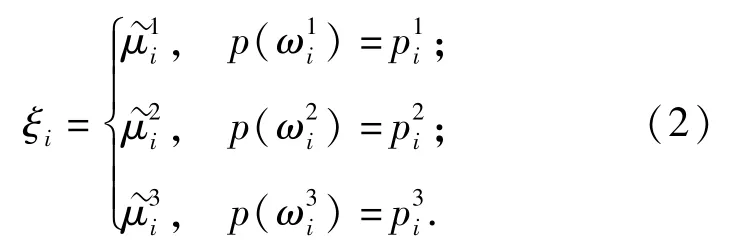
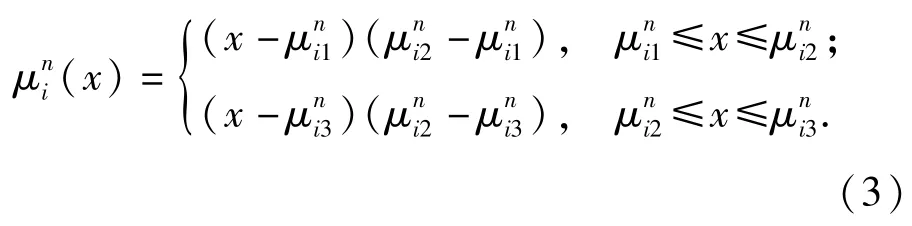
需求待满足节点需要一定数量的资源来支撑保障任务,该类资源需要在一定时限内配送到目标位置才能发挥保障作用,假定资源需求节点资源满足许可延时为

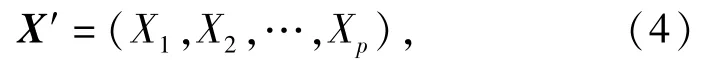
是p×1的随机变量,均值为

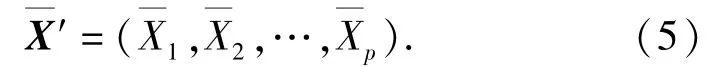
该模型可写成:

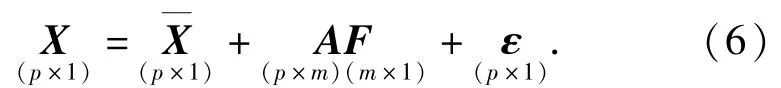
资源需求节点运输时间需求模型可以具体写成:

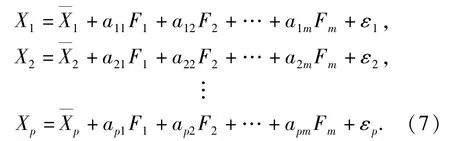
结合非战争军事行动实际,将优化目标设为受灾节点资源未满足数量最小且满足及时度最高。

2.1 边界条件设定

设不同车辆保障资源可以同时运输,失效路段修复和新路段开辟作业在运输优化开始前完成,除特殊路况外,所修复和开辟道路能允许两辆车并行通过,对非战争军事行动车辆装备保障边界条件(见表1)设定如下:

1)保障资源到达资源需求节点,立即发挥保障作用,不存在多项资源相互竞争排队等待的状况,所有保障装备一旦报废,及时停止使用,不考虑报废装备改变功能,代替其他保障物资器材,从而使保障资源部分节约的情况。

2)所有保障人员的知识、经验和保障能力具有同质性,各节点保障人员随机分配,在奔赴任务爆发区域前进行过专业的培训,不存在专业不对口造成配属装备不会使用,从而导致保障能力不能正常发挥的情况。由于非战争军事行动保障任务遂行时间相对于训练时间较短,大部分保障能力来源于平时组训、任务前集训和任务后总结,暂不考虑保障过程中保障人员技能逐渐娴熟带来保障器材装备节约的状况。

3)资源需求待满足节点资源到达时间超过给定最大延时后,其对非战争军事行动装备保障带来的保障效果降低用惩罚因子来描述,定义惩罚同延时时长和未满足资源数量积成正比,即惩罚为δki·rki.

4)上个周期未满足保障资源数自动传递到下个保障周期,不考虑由于保障资源缺乏造成非战争军事行动任务遂行装备过度耗损,从而导致保障资源需求量大幅度增加的情况。

表1 蒙特卡洛仿真模型边界条件Tab.1 Boundary conditions of Monte Carlo simulation model

假定装备保障各自变量相互独立,暂不考虑资源运输相互干扰,影响保障效率的因素。

2.2 仿真运算目标结果

1)失效路段修复和新路段开辟集合;

2)最优车辆保障资源运输路径集合;

3)资源未满足的状况。

2.3 保障资源调度优化函数设置

根据非战争军事行动任务装备保障的要求,在保障资源相同的条件下,尽可能提高保障效果。将优化目标设定为:同等资源供给条件下,资源需求节点资源未满足数最小,超过最大可承受延时时间最小,将需求函数模糊化,即

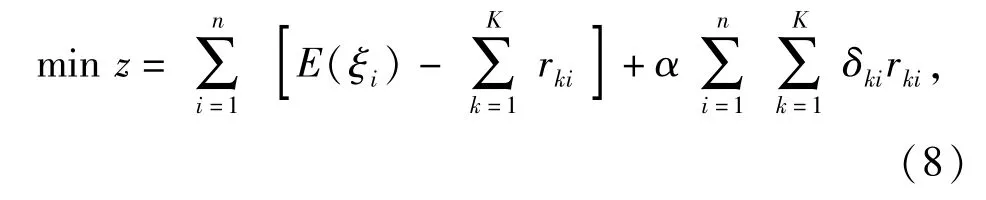
2.4 保障资源优化约束条件

1)运输容量约束

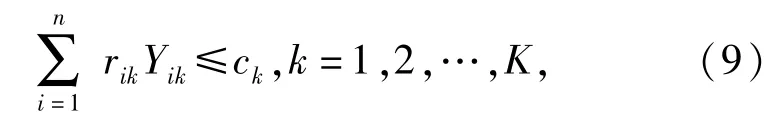
式中:i,j∈V,k∈K;rik是第k次运输中第i个节点的资源需求量;Yik是第k次运输中第i个节点的资源运输率;ck为单次最大运输容量。

2)运输行程约束

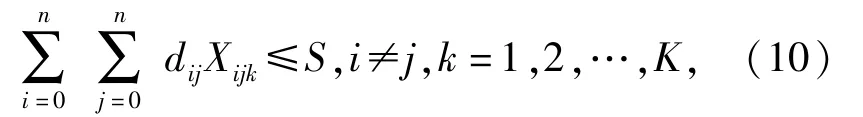
式中:dij为第i个节点到第j个节点之间的距离;Xijk为第k次运输中第i个节点到第j个节点的行驶次数;S为单次最大行程。

3)资源消耗约束

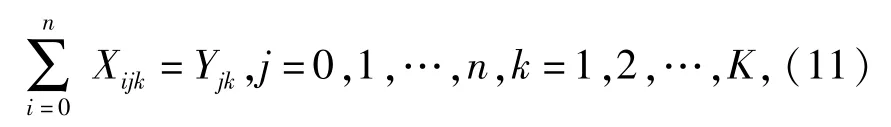
式中:Yjk第k次运输中第j个节点的最大延时。

4)资源数量约束

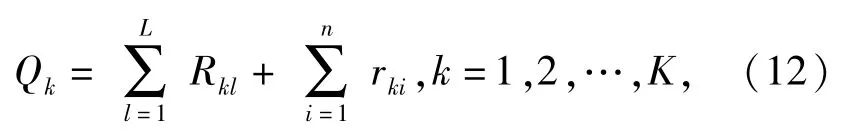
式中:Qk为第k次运输中资源需求量;Rkl为第k次运输中修复第l条道路的资源需求量。

5)延误时间约束

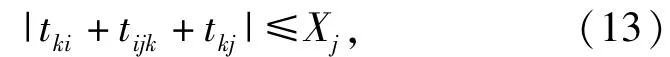
式中:tki为第i个节点出发资源准备时间;tijk为第k次运输中第i个节点到第j个节点所需的运输时间; tkj为第j个节点物质接收时间;Xj为第j个节点保障资源最大延时。

3 遗传算法寻优

3.1 路网寻优

当失效路段数量较多时,路网结构复杂度成几何级数增长,难以求解,为了保证优化结果收敛,做以下寻优设定:

1)车辆装备保障资源调度染色体编码。令车辆装备保障资源调度过程中待修复或开辟道路的数目和染色体结构相同,通过计算机随机发生器,生成非战争军事行动车辆装备保障运输网络路网层染色体,经过遍历算法遍历,生成待优化染色体。

2)车辆装备保障资源调度参数设定。参数设定的目的是使整个运输网络结构最优,即利用最小的资源消耗,实现资源需求节点总体未满足数最小,延时最小,初次寻优是大尺度搜索路网修复最优解的过程。由保障资源约束条件可知,路径层最优解即目标函数为最小值,为了强化寻优效果,设定适应度参数ξi为保障资源调度优化函数的倒数,即

步骤1 资源需求节点资源需求量j数据初始化,令E=0.

步骤2 采用随机-放回-有重复方式从样本空间中抽取样本,结合ξi的概率分布,生成资源需求节点资源需求向量

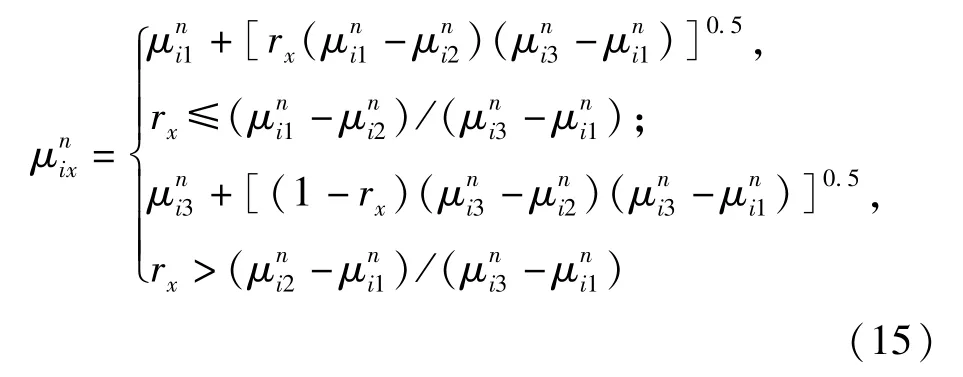
步骤4 重复步骤2～步骤3共MM次。

步骤5 E(ξi)=E/MM.

迭代次数影响路网寻优效果,为了保证寻优结果的可信性,设定第N次寻优和第N-1寻优结果差异小于显著水平5%,N≥5 000.

3)为了达到全局搜索能力,扩大数据选择量,提高算法的性能,采用轮盘赌策略实现最优种群的保留。

4)达到最大进化代数时,令算法终止。

3.2 运输策略寻优

在路网寻优结果的基础上,对运输策略寻优进行迭代,直到寻优结果不再发生明显变化:

1)运输策略寻优初始化。利用需求节点需求表示运输策略寻优染色体基因,染色体基因的排列表示单次运输具体行驶路线,随机不重复反复生成染色体,运用保障策略优化约束条件对初始种群进行可行性鉴定,不符合要求的初始种群予以去除,构成运输策略寻优初始种群,种群交叉变异过程如图1所示。

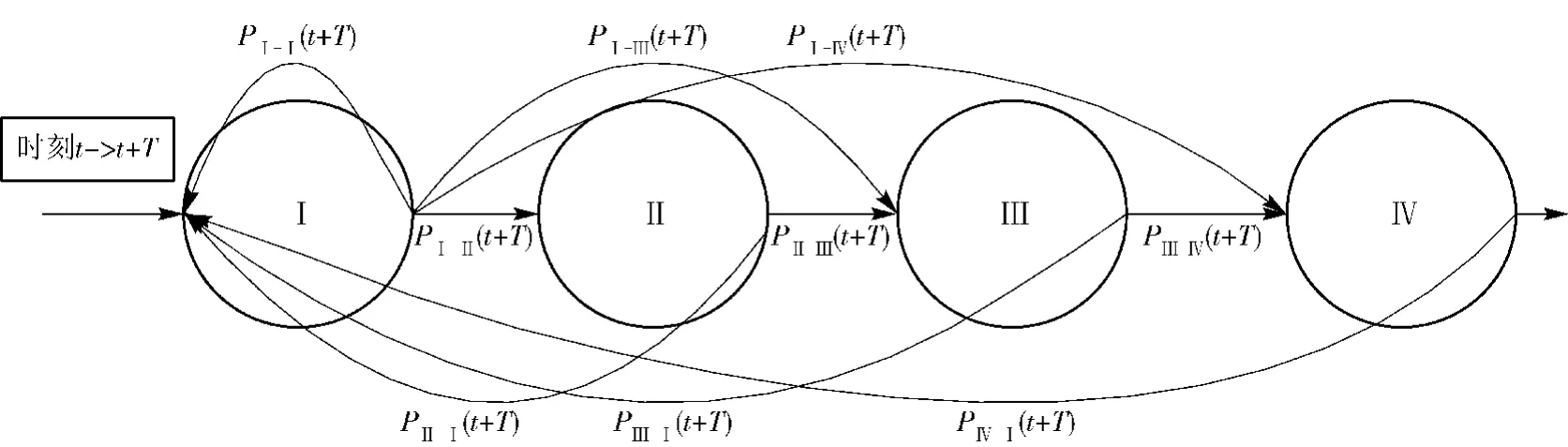
图1 运输策略寻优交叉变异示意图Fig.1 Schematic diagram of transport strategy optimization variation

图1中,Ⅰ、Ⅱ、Ⅲ、Ⅳ分别代表不同的种群,PX-Y(t+T)指的是X种群个体通过交叉、变异和重组,其染色体编码变为Y种群中个体染色体编码的概率。

2)动态寻优过程设定。为了实现寻优结果的快速收敛,对寻优过程进行设定。在初始寻优阶段,将族群中前N个优秀个体中直接复制到下一代族群空间,以此减少交叉变异过程,避免寻优结果在某一局部过久滞留,避免寻优算法陷入无限局部最优的死循环。在初始寻优的基础上,进行该点局部的精细化寻优,对每个寻优结果进行交叉变异,实现寻优结果的全局大尺度最优和局部精细化最优,并保证寻优结果收敛,其过程为:

①将寻优过程划分为两阶段。设ρ∈[0,1),最大进化代数为G,阶段控制点设为G1.全局寻优阶段为[0,G1],局部寻优阶段为[G1,G],G1= INT(ρG),INT取整函数。

②寻优策略设定。设 σ∈[0.5,1),取N= INT(σP),其中 P为种群规模,第一阶段若N＞INT(σP),则N=N-3,否则N=INT((1-σ)P);第二阶段若N＞INT((1-σ)P),则N=N-1,否则N=INT((1-σ)P).

3)控制参数设置。pc和pm随适应度值大小而变化,自动控制寻优精度。其表达式为

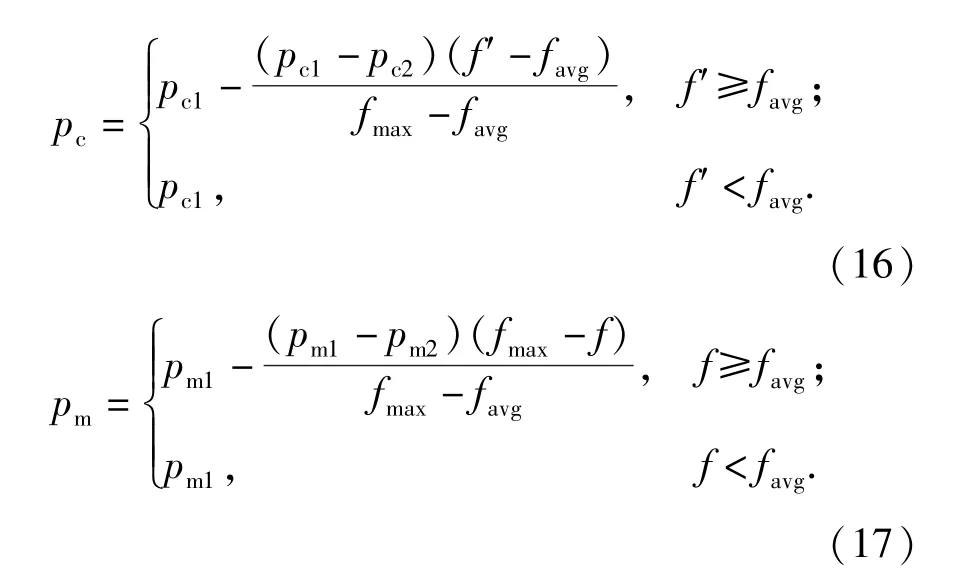
式中:pc1=0.9;pc2=0.6;pm1=0.1;pm2=0.001;f为族群进化代值。为了防止最优结果发生变异,将每次寻优最优结果直接复制入下一代,对次优结果进行交叉变异,当代间的解无明显变化时(经验值取显著水平＜5%),令寻优结束。

4 算例分析

假设我国四川某地区的某区域发生了比较严重的地震灾害,其受灾点有9处,分别用A～I表示,直线为现存交通连接情况,如图2所示。图2中A～I为资源需求节点,1～7为保障节点,为了降低模型复杂性,将地形起伏路段道路归一化,通过等耗时行驶方式,将起伏路段距离变换为平坦路段距离;在大量运输过程中,车辆载重近似服从正态分布,单次车辆载重的变化对整体优化效果的影响较小,暂不考虑单次车辆货物载重对平均行驶速度的影响,假定所有道路平均行驶速度相同,用v表示。

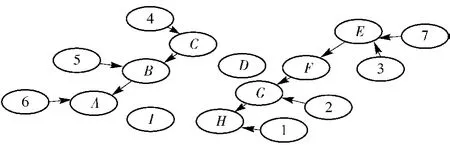
图2 原非战争军事行动任务区域道路情况Fig.2 Road condition of original military operation other than war mission region

灾区所需的保障力量包括器材、装备、人员、水、食物和设备。考虑到每个资源需求节点受类型、严重程度不同,利用随机数发生器,对所有资源需求节点进行[0-1]为中心的随机分布生成,模拟灾害发生时各节点的不同保障需求。

4.1 条件设置

为了使模型更好的反映车辆装备保障运输网络现实,对模型进行参数设置,得到受灾区域的受灾情况,通过运算,对提出的模型进行验证。为了便于模型运算,将保障资源需求、物资运行时间、运行距离、经费消耗等因素进行无量纲化处理,统一规划为单位资源、单位时间、单位距离和单位耗费。

通过计算机随机数生成器生成各资源需求节点资源需求如表2所示,A～I为9个资源需求节点的物质需求量,数据为经归一化后的物质单位运输空间需求量,各种物质混用性差,通过混搭运输节省空间利用效率低,由于非战争军事行动物资需求时效性要求高,混搭运输对时间要求依赖性高,计算中暂不考虑多种物资综合运输节省所占空间情况。

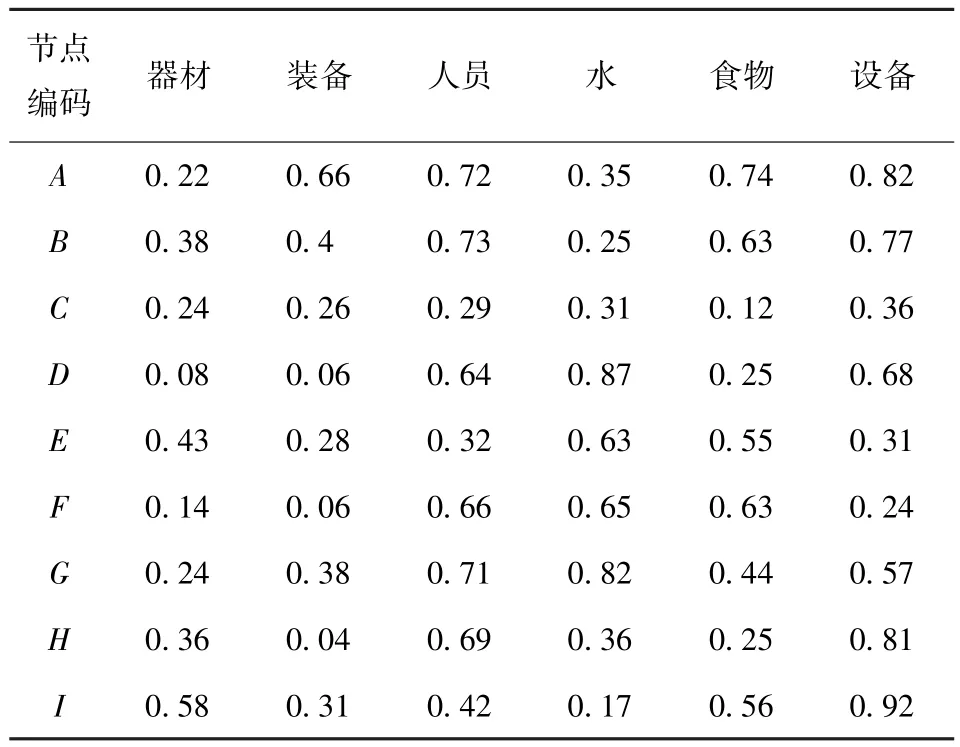
表2 各资源需求节点对资源的需求量Tab.2 Desired resource quantity of resource need nodes

实际运算中,资源需求节点的资源需求量、最高满足时限、失效路段修复、新路段开辟所需要资源量等初始数据,由计算机随机数发生器按照现实受灾情况模拟产生,如表2所示,道路交通情况、路网规划情况在初始数据的基础上通过模型计算生成。修复失效路段v2-v3、v3-v6、v4-v5、v7-v9、v9-v15、v0-v13、v11-v12和v20-v21所需的资源量分别为2、3、1、4、9、4、6和2.

在模型规划中,车辆行驶速度恒定,不同节点之间距离由路网中不同节点实际距离测得,不同节点间运输物资耗时不同,失效路段未完全修复前、新开辟路段施工结束前视为无效路段,不能运输保障资源,未修复路段不能运送资源,一个周期结束时各节点未满足保障资源数,转交给下一个周期。

4.2 运算结果分析

Anylogic软件是以UML-RT、Java和微分方程为基础开发的一款虚拟原型环境、离散连续混合系统仿真工具,支持混合状态编程,能够有效的描述随机不连续的问题[12]。因此选择Anylogic软件对所构建模型进行分析和实现。

在上述条件下,利用Anylogic中的UML仿真工具构建如图2所示原非战争军事行动任务区域道路交通情况模型,代入失效路段修复资源需求量数据和资源需求节点资源需求量数据,计算各节点需求期望、资源未满足数和最大延误时间,如表3所示。

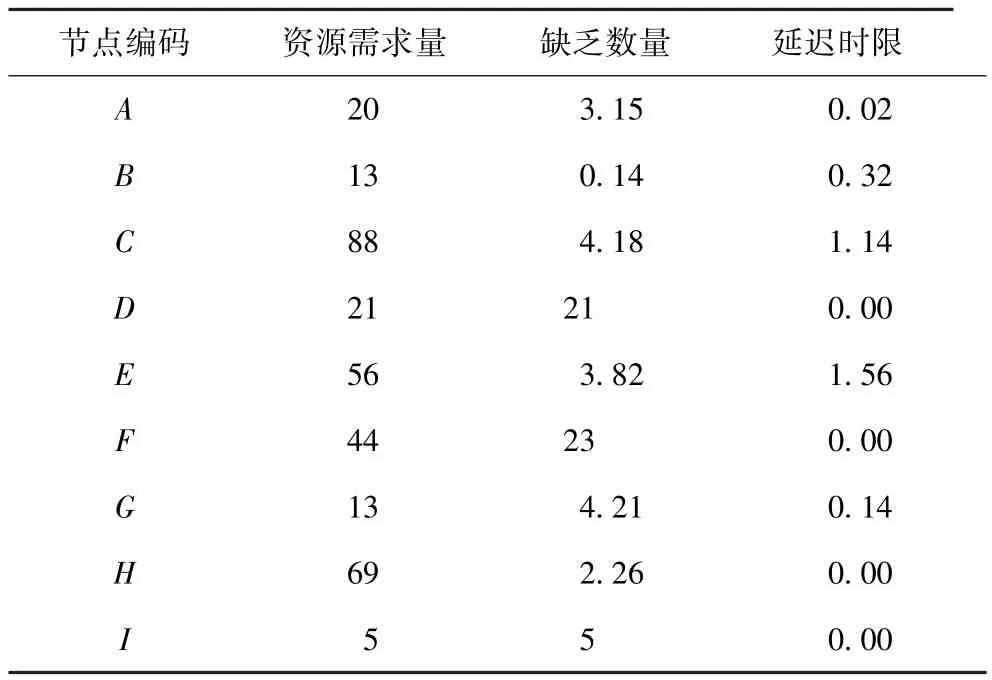
表3 资源待满足节点所需资源状况Tab.3 Resources status of resources to be meet nodes

经过路网优化,得到结果如图3所示,实线为爆发后,留存的可用路网交通情况,虚线为经过路网优化后修复和新开辟的道路情况。

经过运输策略优化后,得到不同染色体结构下,最优运输路径方案如表4所示,从表中可以看出,不同染色体结构下,最优运输路径不同。

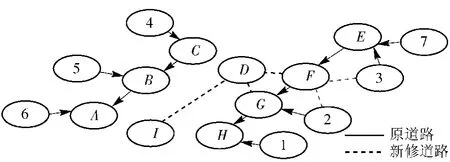
图3 修复后非战争军事行动任务区域道路情况Fig.3 Road condition of military operation other than war mission region after repair

表4 不同染色体结构下的最优路径Tab.4 The optimal paths under different chromosome structures

表4中最优路径为从保障节点到资源待满足节点之间,可供选择的最优运输路径,最优路径的第一个节点为保障节点,最后一个节点为资源待满足节点,中间的节点为转运节点。以v3→vF→vG→vH为例,指的是从节点3出发,经节点F、G转运,到达节点H的路径。

从表5中可以看出,随着延时惩罚因子α的取值不同,路网优化方案效益不同。当α取值较小(α=0.2)时,染色体1条件下minz值最小,说明惩罚因子较小时,部分修复关键道路对于整体效益最大效果最优,存在少修复道路,通过消耗时间转运多个节点,实现整体效益的最大化;当α取值较大(α=0.8)时,染色体3条件下的min z值最下,说明惩罚因子较大的情况下全部修复道路对于整体效益最大效果最优,存在通过消耗资源换取保障时间的情况。

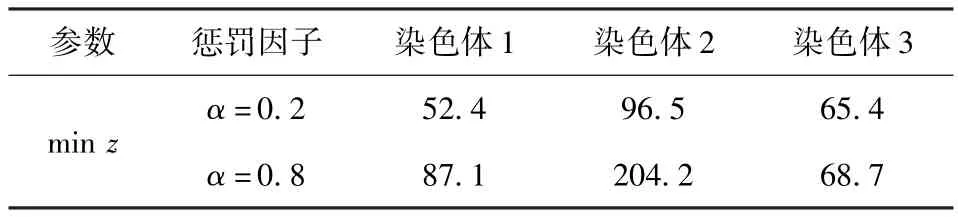
表5 不同染色体下min z值对比Tab.5 Different min z values under different chromosomes

最后利用残差分析,对模型描述8个资源需求节点需求进行分析,如表6所示。表中各资源需求累计解释方差为97.4%,大于经验值95%,说明模型能够较好的解释各资源需求节点的资源需求情况,模型具有合理性,合理性判断准则如表7所示。

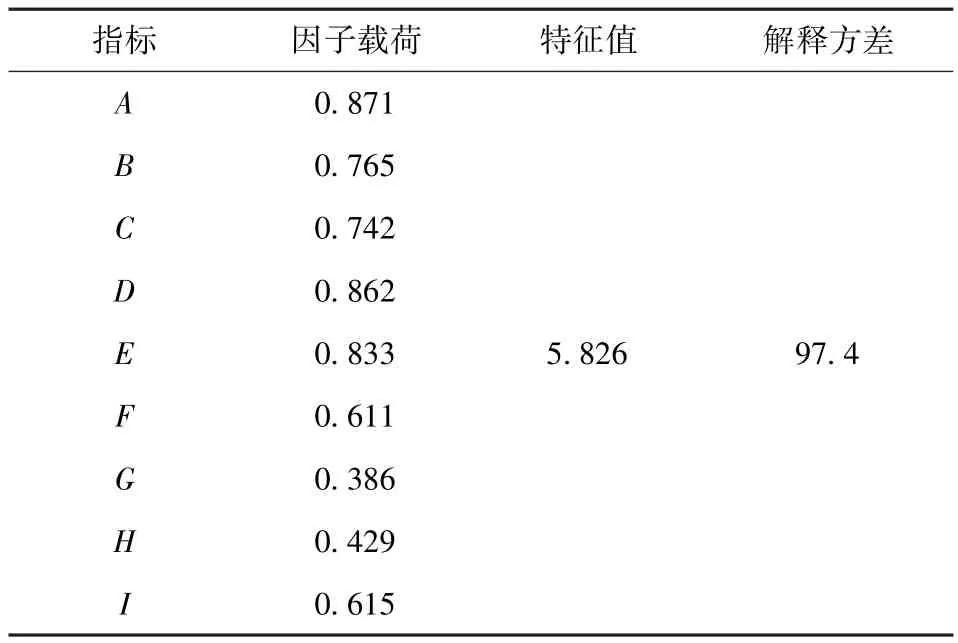
表6 车辆装备保障残差分析结果Tab.6 Residual analysis results of vehicle equipment support

表7 模型支撑性判断准则Tab.7 Model supportability judging criteria

5 结论

针对传统运输网络优化算法不适用于非战争军事行动车辆装备保障问题,提出了基于遗传算法和蒙特卡洛仿真的车辆装备运输网络优化算法,给出了路网修复方案和最优运输路径选择方案,增强了运输网络优化结果的稳定性,揭示了惩罚因子的选取是影响保障方案制定的关键因素,对抗震救灾和抗洪抢险等非战争军事行动车辆装备保障运输效果提升有理论指导意义和技术支撑价值。结合具体灾害类型的车辆装备保障运输网络优化是下一步研究方向。

References)

[1]殷凤军,叶茂,过秀成,等.综合运输网络上多货类流量最短路分配[J].交通运输工程与信息学报,2014,12(1):34-40.YIN Feng-jun,YE Mao,GUO Xiu-cheng,et al.Shortest path distribution of Multi-class cargo flow on a comprehensive transport network[J].Journal of Transportation Engineering and Information,2014,12(1):34-40.(in Chinese)

[2]Huang J,Wang Y G,Chen X B,et al.Current status of medical support in military operations other than war in domestic and overseas[J].Journal of Medical of Colleges of PLA,2012,27(6): 343-350.

[3]马燕,崔人伟,李海英.非战争军事行动装备器材集装化应急保障探析[J].包装工程,2011,33(23):76-83.MA Yan,CUI Ren-wei,LI Hai-ying.On materiel containerization emergency support in non war military operations[J].Packaging Engineering,2011,33(23):76-83.(in Chinese)

[4]任鑫,周碧松,孔衍,等.基于灰色预测模型的核事故医学应急装备使用保障费用分析[J].数学的实践与认识,2013,43(19):173-179.REN Xin,ZHOU Bi-song,KONG Yan,et al.Usage and guarantee expenses analysis of nuclear accident medical emergency equipment base on gray prediction model[J].Mathematics in Practice and Theory,2013,43(19):173-179.(in Chinese)

[5]陈春良,齐鸥,刘彦,等.基于因子分析和结构方程建模的应急装备保障能力指标优化[J].计算机测量与控制,2015,23(6):2037-2041.CHEN Chun-liang,QI Ou,LIU Yan,et al.Index optimization of emergency equipment support ability based on factor analysis and structural equation modeling[J].Computer Measurement&Control,2015,23(6):2037-2041.(in Chinese)

[6]熊云,李晓勇,李宏伟,等.非战争军事行动对我军军品包装发展的影响与对策[J].包装工程,2011,31(21):119-122.XIONG Yun,LI Xiao-yong,LI Hong-wei,et al.Impact of military operation other than war on the development of military packaging and countermeasure[J].Packaging Engineering,2011,31(21):119-122.(in Chinese)

[7]杨志谋,司光亚,刘德胜,等.战略模拟系统中计算机生成人口研究[J].计算机工程与应用,2011,47(18):212-214.YANG Zhi-mou,SI Guang-ya,LIU De-sheng,et al.Research on computer generated population in virtual global war space[J].Computer Engineering and Applications,2011,47(18):212-214.(in Chinese)

[8]Ning H,Shi Y B,Gao X J.Dynamic simulation of the equipment repair support system[J].Procedia Engineering,2011,23(2): 284-289.

[9]周骞,周霞,刘军,等.基于畅通可靠度的城市物流配送运输网络优化研究[J].公路工程,2011,36(2):38-42.ZHOU Qian,ZHOU Xia,LIU Jun,et al.Study on optimization of urban transportation logistics distribution network based on the analysis of unblocked reliability[J].Highway Engineering,2011,36(2):38-42.(in Chinese)

[10]陈康,杨忠振.基于用户平衡理论的水陆混合运输网络的交通量分配方法[J].大连海事大学学报,2012,38(2):33-36.CHEN Kang,YANG Zhong-zhen.A traffic assignment method for water and land mixed transportation network based on user equilibrium principle[J].Journal of Dalian Maritime University,2012,38(2):33-36.(in Chinese)

[11]吴琼,郑士源,朱太球.基于列生成算法的集装箱班轮运输网络优化[J].上海海事大学学报,2014,35(1):29-34.WU Qiong,ZHENG Shi-yuan,ZHU Tai-qiu.Container liner shipping network optimization based on column generation algorithm[J].JournalofShanghaiMaritimeUniversity,2014,35(1): 29-34.(in Chinese)

[12]吴中,施雯.基于Anylogic的行人换乘通道入口优化设计[J].贵州大学学报:自然科学版,2013,30(6):130-133.WU Zhong,SHI Wen.Optimization design of pedestrian transfer channel entrance based on anylogic[J].Journal of Guizhou University:Natural Sciences,2013,30(6):130-133.(in Chinese)

Vehicle Equipment Support Transport Net Optimization Model Based on Monte Carlo Simulation and Genetic Algorithm

CHEN Chun-liang,QI Ou,WEI Zhao-lei,LIU Yan
(Department of Technique Support Engineering,Academy of Armored Force Engineering,Beijing 100072,China)

The vehicle equipment support transport net is the key segment that impacts the mission completion of the military operation other than war.The tranditional method may result in the unstable results in its application in the optimization of vehicle equipment support transport net are obtained because of the poor ability of to describe the random and discontinuous support needs.An optimization model of vehicle equipment transport net is proposed based on Monte Carlo simulation and genetic algorithm.The boundary condition,support resource scheduling optimization function and support resource restraint condition are set according to the support feature of military operation other than war.An optimization model of vehicle equipment transport net is constructed.Finally,the efficiency of the proposed model is verified by residual analysis.

ordnance science and technoogy;Monte Carlo simulation;genetic algorithm;vehicle equipment support;transport net optimization

TB114.3

A

1000-1093(2016)01-0114-08

2015-04-06

总装备部预先研究项目(2015年)

陈春良(1963—),男,教授,博士生导师。E-mail:chenchunliang1963@gmail.com;齐鸥(1987—),男,博士研究生。E-mail:haikuotiankongru@163.com