样品选择结合分段直接校正法和偏最小二乘法用于近红外光谱分析模型传递研究

王菊香,孟凡磊,刘林密,崔伟成

(海军航空工程学院飞行器工程系,山东烟台264001)

样品选择结合分段直接校正法和偏最小二乘法用于近红外光谱分析模型传递研究

王菊香,孟凡磊,刘林密,崔伟成

(海军航空工程学院飞行器工程系,山东烟台264001)

为了实现近红外光谱分析模型在不同仪器间的共享,对分析模型的传递方法进行了研究。以混胺燃料的分析模型为例,采用马氏距离法对转换集样品进行选择,采用分段直接校正(PDS)法结合偏最小二乘(PLS)法,对从仪器光谱进行校正。对转换集样品数、PLS回归的主因子数、PDS的窗口宽度进行选择,当转换集样品数为12、主因子数为1、窗口宽度为39时,转换集样品的光谱校正率达到96.5%.混胺分析模型传递后,预测集样品的标准偏差远远好于校正前的结果,与主仪器的非常接近。研究结果表明:采用马氏距离法选择转换集样品,并结合PDS-PLS算法计算转换矩阵,可有效扣除不同仪器间的光谱差异,提高混胺分析模型的传递精度,实现三乙胺、二甲苯胺、水分、密度的准确分析。

光学;光谱分析;近红外光谱;模型传递;马氏距离法;分段直接校正法;偏最小二乘法;混胺

DOI:10.3969/j.issn.1000-1093.2016.01.014

0 引言

近红外光谱主要是含氢基团(C—H、N—H、O—H)的倍频和合频吸收产生的,波长范围在700～2 500 nm,具有光谱信息丰富,吸收强度较低、谱带重叠的特点。近红外光谱分析是借助于化学计量学方法提取信息,建立多元校正模型,完成对一个对象的多个组分或性质的同时分析,具有样品不用预处理、分析速度快、无污染等特点。目前近红外光谱分析已广泛用于石油、食品、医药等领域[1-4]。近几年,邢志娜等采用近红外光谱技术实现了多种液体推进剂质量的快速检测分析[2]。

但近红外光谱分析在实际应用中会出现这样的情况,在某一仪器或者某一种测量条件下建立的多元校正模型,用在另一台相同型号的仪器上或在其他测量条件下预测结果会产生较大偏差。这是因为测量的光谱不仅包含了样品组分信息,还包含了仪器、测量条件的特性。当仪器的响应函数(包括仪器老化、部件更换、新仪器使用以及测量环境的变化等)发生变化时,所建模型不再适用。解决该问题的方法:一是花费大量的人力和物力重新建立分析模型,这对分析模型种类多、仪器数量多的情况是非常不利的;二是通过数学方法进行模型传递,这是目前近红外光谱研究的热点之一[1]。模型传递就是通过数学的方法将一台仪器所建模型共享到另一台仪器上,实现利用主仪器上的模型准确预测从仪器上的光谱,当需要建模的仪器较多时,模型传递可节省对每台仪器新建模型的工作量。目前比较成熟且应用最为广泛的模型传递算法有Slope/Bias算法、DS算法等[5-6]。本文以液体推进剂混胺的近红外光谱分析为例,研究两台仪器间模型传递的方法。

1 实验过程

1.1 基础数据测定

采用标准分析方法对混胺试样中的密度、水分、三乙胺和二甲苯胺进行测定,多次测定结果取平均值。

1.2 光谱数据采集

NIR-3000近红外光谱仪两台(北京英贤仪器有限公司产,建有分析模型的仪器为主仪器,未建分析模型需进行模型传递的仪器为从仪器),配有5 cm玻璃样品池,CCD/2048像素检测器,波长范围700～1 100 nm(2002波长点)。对混胺试样以空气为参比分别在两台仪器上进行光谱扫描,扫描10次,取平均值。

2 基于马氏距离的转换集样品选择算法

在有标模型传递方法中,首先需要选取转换集样品。转换集样品一般从主仪器上的用于建模的样品集中选择。转换集必须包含足够的信息来校正仪器或测量条件变化造成的偏差,并包含一定的数量。

2.1 算法原理

为了保证不同吸收程度的光谱(即不同浓度或性质范围的样品光谱)都能很好的校正,保证模型传递的精度,需选择样品集中差异较大的光谱进行校正。欧氏距离法是一种计算样品的光谱差异来选择转换集样品的常用算法[7-8]。欧氏距离法便于分析和计算,但当变量多重相关造成信息重叠时,欧氏距离法会片面强调某些变量的重要性。近红外光谱是含氢基团的倍频吸收峰,呈馒头峰,基团的光谱信息重叠严重。此时欧氏距离法对计算光谱的差异是不利的。马氏距离法与欧氏距离法不同的是,它考虑到各种特性之间的联系[9]。它不仅不受量纲的影响,而且还可以排除变量之间相关性的干扰[10]。基于马氏距离的算法选择转换集样品的具体步骤如下:

步骤1 首先计算两两样本之间马氏距离,挑选出距离最大的两个作为第1个和第2个转换集样品。

步骤2 然后分别计算剩余样品与已选出两个样品之间的距离。

步骤3 对于每个样品,其与已选择样品之间的最短距离被选择,然后选择这些最短距离中相对最长的距离所对应的样本来作为第3个样品。

步骤4 重复步骤3,直到依次选择出的样品个数与事先预定样品个数相等为止。

2.2 转换集样品数量的确定

为了确定选择的转换样品集数量,采用分段直接校正(PDS)算法计算主、从仪器间的转换矩阵,对从仪器采集的光谱进行校正。采用光谱平均差异(ARMS)和光谱校正率Prc评价传递性能[10]。图1为ARMS随转换集样品数量变化曲线。由图1可见,随着转换集样品数的增多,ARMS逐渐下降,但采用马氏距离选择的转换样品集进行的模型传递效果比欧氏距离的要好。由表1可见,两种方法选择样品的顺序是不一样的。当图1中马氏距离法选择的转换集样品数增至12时,ARMS变化幅度趋于平稳,其光谱的校正率可达到96.5%(此时PDS-PLS算法中主因子数为1,窗口宽度39),如图2所示。因此,可选择此12个样品作为模型传递时的转换样品集。

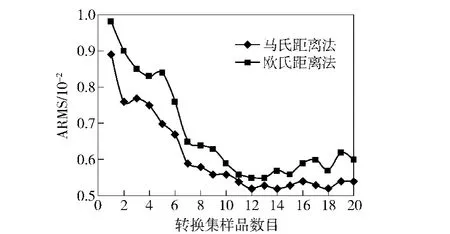
图1 ARMS随转换集样品数的变化图Fig.1 Change of the average of root mean square (ARMS)with the number of transfer sets

表1 基于欧氏距离和马氏距离的转换集样品Tab.1 Ttransfer set samples selected based on Euclidean and Mahalanobis distances

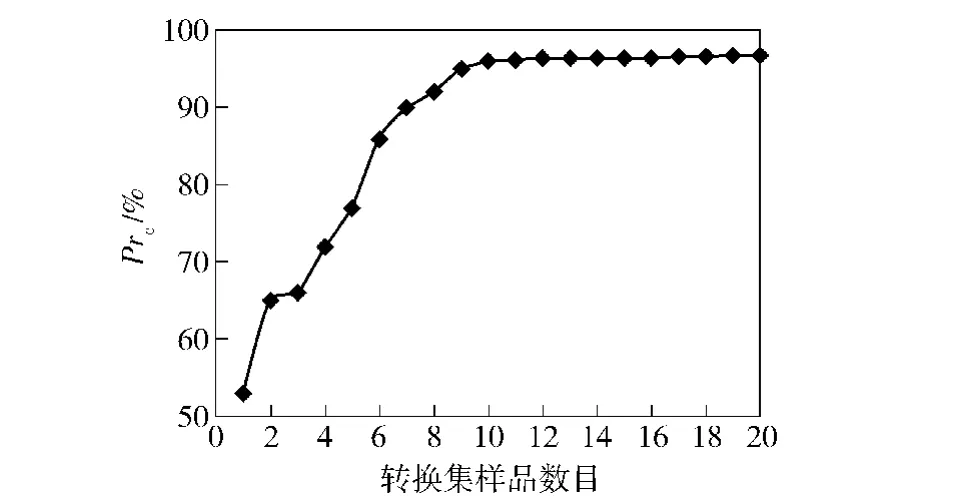
图2 光谱校正率Prc随转换集样品数的变化图Fig.2 Change of Prcwith the number of transfer sets

3 PDS-PLS模型传递算法

3.1 算法原理

PDS算法是一种通过建立主、从仪器间光谱的校正矩阵实现模型传递的多元全光谱标准化方法[11-12]。它的基本思想是主仪器上的光谱矩阵Xms,从仪器上的光谱矩阵Xss,二者在不同条件下和仪器下测定,所以存在一定的差异,通过转换矩阵F将Xss转换成Xms,使二者相匹配。

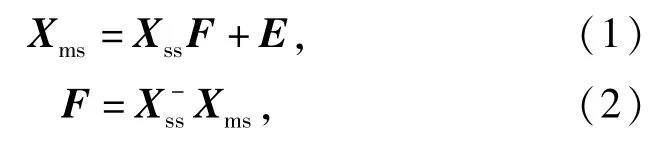
对于实际的光谱数据,波长点的漂移通常只局限于一个小的区域。因此,主仪器上的每个波长点只是与从仪器上相应波长点附近的波长关联大,并不是与全谱区的光谱点都关联。设与主仪器光谱的第i个波长点相关联的从仪器光谱区域为Zi,为了重构主仪器上的每一点,令Zi表示“从仪器"上从i-k到i+k共2k+1个点的吸光度矩阵。

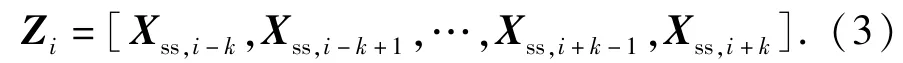
对主仪器上的每一个向量Xi,构造如下多元回归模型:

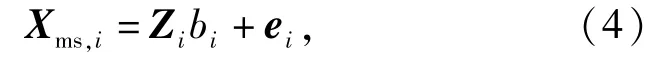
式中:bi为回归系数;ei为残差向量。

此方程由PLS[13]求解所有的回归系数bi,i=1,2,…,p.将所有的回归系数bi置于F的主对角线上,并将其他元素置为0,这样可得到一带状矩阵F:

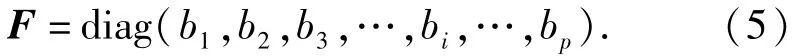
有了转换矩阵F,就可以将从仪器得到的未知样品的光谱Xsu转换成与主仪器光谱相匹配的光谱Xst:

3.2 主因子数选择

使用PLS计算转换矩阵时,主因子数的选择对校正效果的好坏有重要影响[14]。为了确定最佳主因子数,分别用1～10的主因子数对不同窗口w下转换集样品光谱依次计算校正参数,对从仪器的光谱进行校正,以校正后光谱与主仪器光谱的ARMS对主因子数作图,当ARMS最小时,对应的主因子数为当前窗口宽度下最佳主因子数。对在窗口范围3～71(间隔为2)的窗口分别进行主因子数挑选,计算得出在各个窗口宽度下ARMS值均为随着主因子数的增加而增加,且均为主因子数为1时ARMS的值最小,因此在PDS-PLS算法中主因子数确定为1.图3为窗口宽度为39时,不同主因子数下ARMS值的变化曲线,从中可以看出主因子数为1时,ARMS最小,校正效果达到最好。

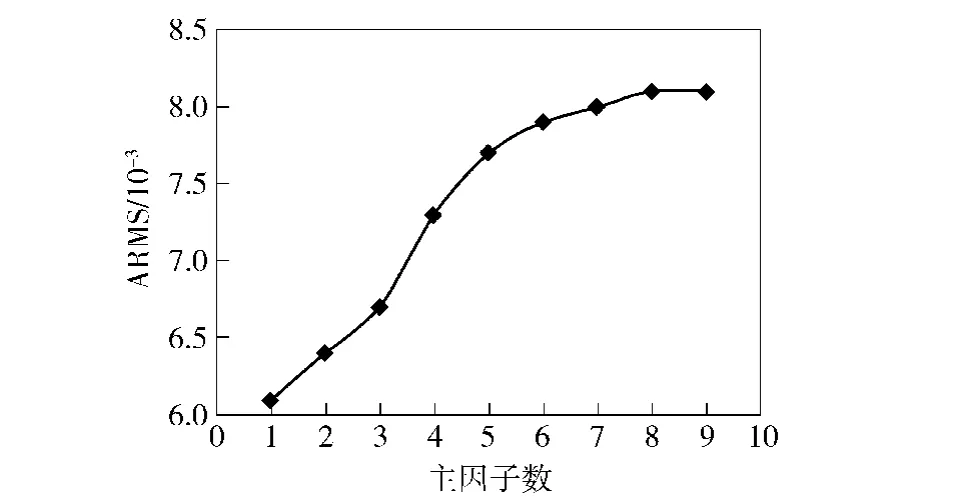
图3 ARMS随主因子数的变化图Fig.3 Change of ARMS with the number of prime factors

3.3 PDS窗口宽度选择

使用PDS算法进行模型传递时,如果窗口宽度w过小,则会出现选定的光谱数据会遗漏仪器之间差异信息,使得传递性能较差;如果窗口宽度w过宽,则选定的光谱数据将包含一些与仪器无关的信息,不仅计算量过大,而且会出现“过校正"的现象,最终使得传递性能变差。所以选择适当的窗口宽度在模型传递中起到重要的作用。图4为PDS-PLS算法校正光谱的ARMS随着窗口宽度w的变化曲线。当w为39时,ARMS最小,校正率最高,因此选定PDS-PLS算法的窗口宽度为39.

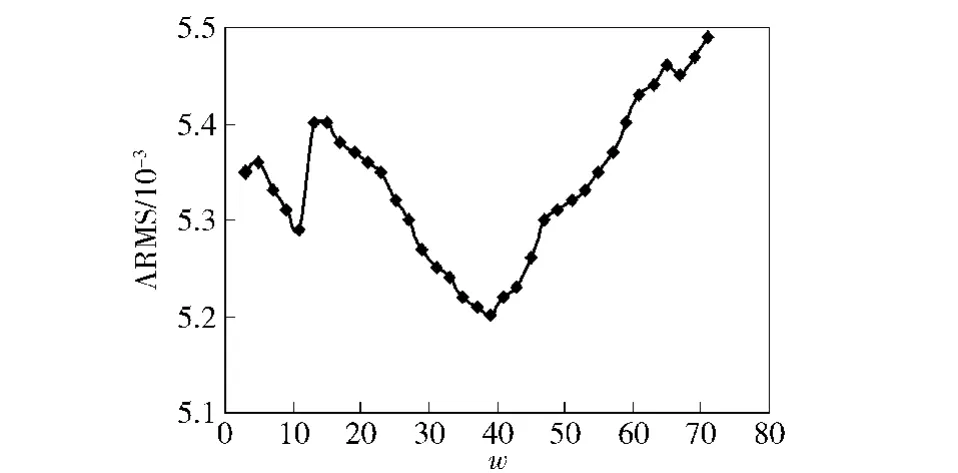
图4 ARMS随窗口宽度的变化图Fig.4 Change of ARMS with the width of window

4 结果分析

4.1 谱图分析

对马氏距离法选择的12个转换集样品,采用PDS-PLS算法在最佳主因子数为1、校正光谱窗口宽度为39的情况下建立转换矩阵。主、从仪器采集的光谱及校正后的光谱如图5所示。由图5可见,同一样品的从仪器光谱经过校正后基本与主仪器光谱重合。从谱图上来看,经过 PDS-PLS算法校正后,主、从仪器间的差异基本消除。

4.2 样品分析

为了进一步检验光谱校正的效果,用主仪器所建分析模型对从仪器采集并进行校正的一组混胺样品(称作预测集)光谱进行预测。对混胺样品的密度、三乙胺、二甲苯胺和水分的预测结果进行分析,通过模型对预测集预测结果的标准偏差(SEP)进行判断[1]。

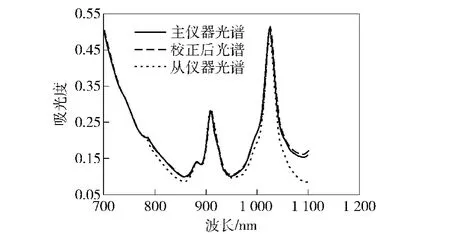
图5 主仪器、从仪器以及校正后的光谱图Fig.5 Spectra from reference and target instruments and calibrated spectra

在PDS-PLS算法的参数选为最佳参数的条件下,分别对预测集在从仪器上测得的光谱和经过PDS算法校正过后的光谱用主仪器的分析模型进行预测分析,并和主仪器本身的预测结果进行对比,如表2所示。结果表明,选择合适的转换集样品后,PDS-PLS算法实现了混胺组分和性质预测分析模型的传递。经 PDS校正后,三乙胺含量的 SEP由0.918降到0.552,二甲苯胺含量的SEP由0.675降到0.347,水分含量的SEP由0.123降到0.065,密度的SEP由0.005降到0.002.混胺各组成和性质的分析模型经PDS-PLS传递后,SEP大幅度地降低,预测精度提高十分明显,已经比较接近主仪器上模型的预测精度。图6～图9分别是经PDS传递前后各组分和性质的预测值与标准方法测定值的相关图。传递前后的相关图比较直观地说明了PDS的校正效果。

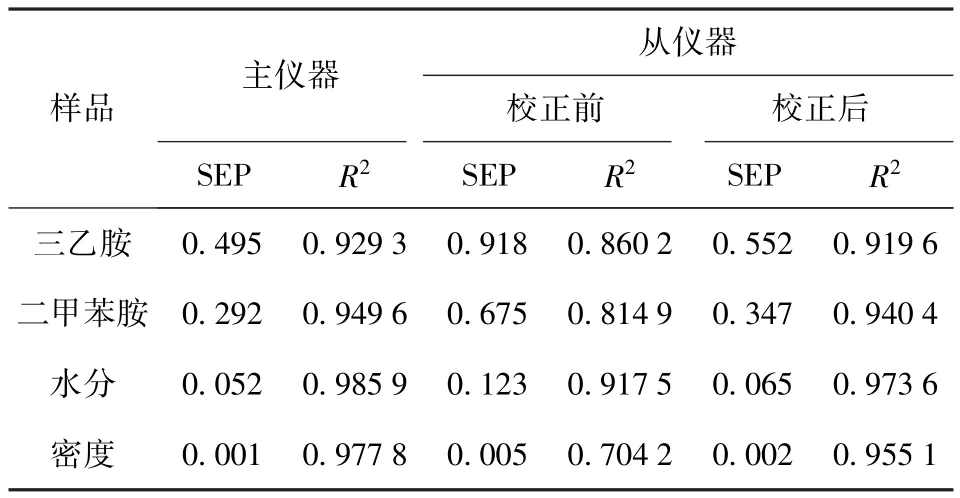
表2 PDS-PLS传递效果分析Tab.2 Results of calibration transfer based on PDS-PLS

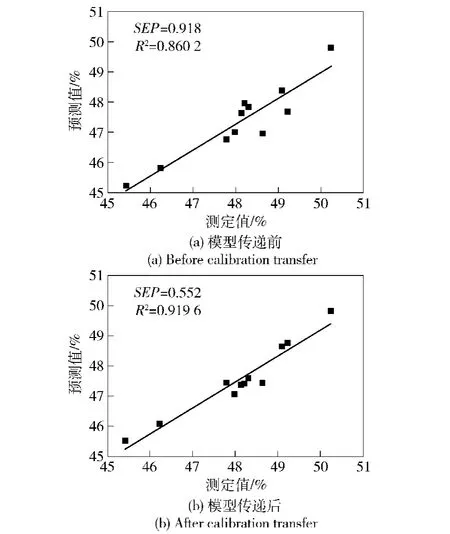
图6 模型传递前后的三乙胺含量的预测值与真实值的相关图Fig.6 Correlograms of measured and predicted triethylamine content

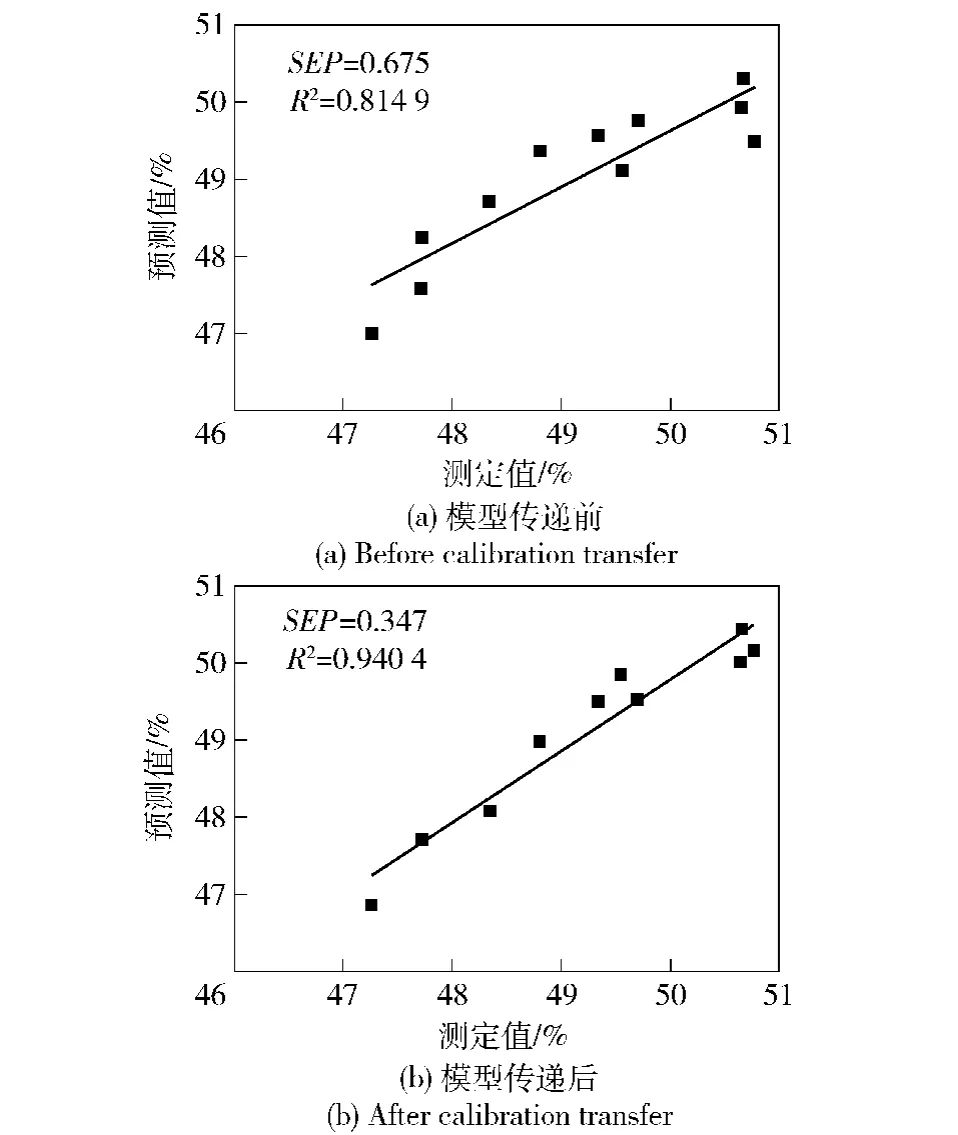
图7 模型传递前后的二甲苯胺含量的预测值与真实值的相关图Fig.7 Correlograms of measured and predicted xylidine content

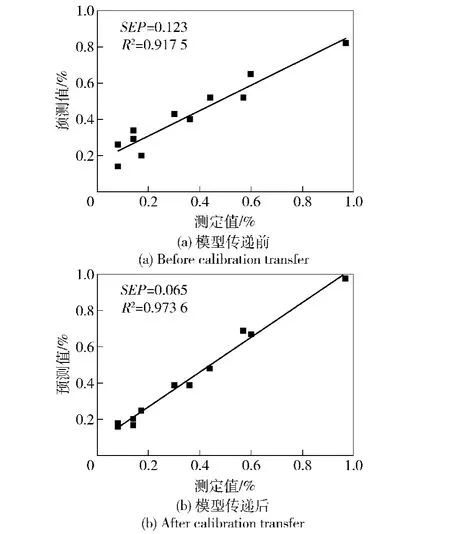
图8 模型传递前后的水分含量的预测值与真实值的相关图Fig.8 Correlograms of measured and predicted water content

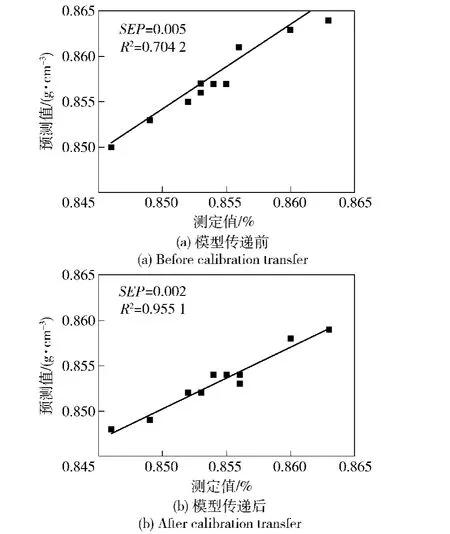
图9 模型传递前后的密度的预测值与真实值的相关图Fig.9 Correlograms of measured and predicted densities

5 结论

与欧氏距离法相比,马氏距离法可不受量纲影响,还可排除变量之间相关性的干扰,有效选择出更具代表性的模型传递转换集样品。PDS算法通过将全光谱分成一定的窗口宽度进行分段校正,可准确地计算光谱间的校正矩阵,结合PLS算法计算回归系数,可进一步消除光谱共线性干扰。对混胺的分析模型进行传递后,主仪器分析模型对从仪器的预测集的校正光谱进行分析,获得三乙胺、二甲苯胺、水分和密度的预测结果的SEP远远好于校正前,基本与主仪器的预测结果接近。混胺分析模型的传递结果表明:通过马氏距离选择合适的转换集样品,采用PDS-PLS算法可有效扣除不同仪器间的光谱差异,实现近红外光谱分析模型在主、从仪器间共享,为其他液体推进剂分析模型的传递提供了一种有效的途径,为近红外光谱分析技术在各部队液体推进剂质量检测中的广泛应用节省了大量资源。

References)

[1]陆婉珍.现代近红外光谱分析技术[M].北京:中国石化出版社,2007.LU Wan-zhen.Modern NIRS analysis technology[M].Beijing: China Petrochemical Press,2007.(in Chinese)

[2]邢志娜,王菊香,申刚.改进偏最小二乘法在航空煤油的近红外光谱分析中的应用[J].兵工学报,2010,31(8):1106-1109.XING Zhi-na,WANG Ju-xiang,SHEN Gang.Application of improved partial least squares method in near-infrared spectrum analysis for aviation kerosene[J].Acta Armamentarii,2010,31(8): 1106-1109.(in Chinese)

[3]Wu D,Chen X J,Shi P Y.Determination of α-linolenic acid and linoleic acid in edible oils using near-infrared spectroscopy improved by wavelet transform and uninformative variable elimination[J].Analytica Chimica Acta,2009,643(2):166-171.

[4]Jing M,Cai W S,Shao X G.Multiblock partial least squares regression based on wavelet transform for quantitative analysis of near infrared spectra[J].Chemometrics and Intelligent Laboratory Systems,2010,100(1):22-27.

[5]李庆波,张广军,徐可欣,等.DS算法在近红外光谱多元校正模型传递中的应用[J].光谱学与光谱分析,2007,27(5): 873-876.LI Qing-bo,ZHANG Guang-jun,XU ke-xin,et al.Application of DS algorithm to the calibration transfer in near-infrared spectroscopy[J].Spectroscopy and Spectral Analysis,2007,27(5):873-876.(in Chinese)

[6]Pereira C F,Pimentel M F,Galvao H K R.A comparative study of calibration transfer methods for determination of gasoline quality parameters in three different near infrared spectrometers[J].Analytica Chimica Acta,2008,611(1):41-47.

[7]Groot P,Melssen W,buydenss L,et al.Selecting a representative training set for the classification of demolition waste using remote NIR sensing[J].Analytica Chimica Acta,1999,392(1):67-75.

[8]Smith M,Jee R,Moffat A,et al.A procedure for calibration transfer between near-infrared instruments-a worked example using a transmittance single tablet assay for piroxicam in intact tablets[J].The Analyst,2004,129(9):806-816.

[9]Mahalanohis P C.On the generalized distance in statistics[J].Proceedings of the National Institute of Science India,1936,12(1):49-55.

[10]李华,王菊香,邢志娜,等.改进的K/S算法对近红外光谱模型传递影响的研究[J].光谱学与光谱分析,2011,32(2): 362-366.LI Hua,WANG Ju-xiang,XING Zhi-na,et al.Influence of improved Kennard/Stone algorithm on the calibration transfer in near-infrared spectroscopy[J].Spectroscopy and Spectral Analysis,2011,32(2):362-366.(in Chinese)

[11]田高友,褚小立,袁洪福,等.小波变换-分段直接校正法用于近红外光谱模型传递研究[J].分析化学,2006,34(7): 927-932.TIAN Gao-you,CHU Xiao-li,YUAN Hong-fu,et al.Application of wavelet transform-piecewise direct tandardization on the near infrared analysis model transfer[J].Chinese Journal of Analytical Chemistry,2006,34(7):927-932.(in Chinese)

[12]Griffiths M L,Svozil D,Worsfold P.The application of piecewise direct standardization with variable selection to the correction of drift in inductively coupled atomic emission spectrometry[J].Journal of Analytical Atomic Spectrometry,2006,21(10): 1045-1052.

[13]Haavisto O,Hyotyniemi H.Recursive multi-model partial least squares estimation of mineral flotation slurry contents using optical reflectance spectra[J].AnalyticaChimicaActa,2009,642(1):102-109.

[14]褚小立.化学计量学方法与分子光谱分析技术[M].北京:化学工业出版社,2011.CHU Xiao-li.Molecular spectroscopy analytical technology combined with chemometrics and its applications[M].Beijing: Chemical Industry Press,2011.(in Chinese)

Application of Sample Selection and PDS-PLS Algorithms in Near Infrared Spectra Analysis Model Transfer

WANG Ju-xiang,MENG Fan-lei,LIU Lin-mi,CUI Wei-cheng
(Department of Airborne Vehicle Engineering,Naval Aeronautical and Astronautical University,Yantai 264001,Shandong,China)

A transfer method of near infrared(NIR)spectra analysis model is studied in order to enable one instrument(reference instrument)and the other one(target instrument)to share the model.The transfer set samples are selected with Mahalanobis distances by taking an analysis model of mixed-amine fuel for example,and the algorithm of piecewise direct standardization(PDS)combined partial least squares(PLS)is used to set the spectral correction matrix between the reference and target instruments.The number of transfer samples,the number of prime factors of PLS regression and the window width of PDS are confirmed based on the average of root mean square(ARMS)of corrected spectra of transfer samples.The corrected rate of spectra of transfer samples reachs 96.5%with transfer sample number of 12 and prime factor number of 1 and window width of 39.Standard deviation of prediction set(SEP)of every analysis item on target instrument is near SEP on reference instrument after the analysis model of mixed-amine is transferred,the transferred model can predicate triethylamine content,xylidine content,water content and density accurately.The results indicate that the sample selection based on Mahalanobisdistances and PDS-PLS algorithms can deduct the difference of NIR spectra among instruments and improve the analytical accuracy of NIR model.

optics;spectral analysis;near infrared spectra;model transfer;Mahalanobis distance; piecewise direct standardization;partial least squares;mixed amine

O657.33

A

1000-1093(2016)01-0091-06

2015-04-21

王菊香(1971—),女,教授。E-mail:juxiangw@163.com