某型无人机三维空间航迹跟踪控制方法研究

管军,易文俊,常思江,梁振东,吕一品

(1.南京理工大学瞬态物理国家重点实验室,江苏南京210094;2.南京理工大学能源与动力工程学院,江苏南京210094)

某型无人机三维空间航迹跟踪控制方法研究

管军1,易文俊1,常思江2,梁振东1,吕一品1

(1.南京理工大学瞬态物理国家重点实验室,江苏南京210094;2.南京理工大学能源与动力工程学院,江苏南京210094)

研究某型无人机三维空间航迹跟踪问题,通过在理想航迹上选取一系列航迹点,将航迹跟踪问题转换为航迹点跟踪问题。建立了无人机的动力学模型,将无人机的速度坐标系对准航迹点所在的理想坐标系,使位置跟踪问题转化为姿态跟踪问题。推导了无人机的制导律,并利用滑模变结构控制理论和反步控制理论分别设计了姿态控制器和速度控制器,姿态控制器使飞行器的速度矢量方向对准航迹点所在的方向,然后利用速度控制器控制速度的大小使飞行器到达预定航迹点。对整个制导、控制系统进行了全系统仿真,仿真结果表明:所设计的控制器具有较高的跟踪精度,且具有较强的抗干扰能力。

控制科学与技术;反步控制;滑模变结构控制;无人机;航迹点跟踪;Lyapunov函数

DOI:10.3969/j.issn.1000-1093.2016.01.010

0 引言

无人机在军用和民用领域均有广阔的应用前景,如何更好地提高无人机的自主控制能力已经成为当前国内外研究的热点问题。

目前国内外很多学者已经对无人机的控制问题进行了广泛的研究。Enns等[1]在小型无人机控制律设计中应用了非线性动态逆控制,Sieberlin等[2]在整个飞行包线内将动态逆理论与增益调节控制方法相结合设计了控制律,并取得良好的效果,刘芳等[3]采用鲁棒动态逆方法对自旋导弹控制系统进行设计,陶冶等[4]设计了带死区变增益PID自适应控制律,刘重等[5]将反步法和非线性动态逆结合起来实现了某型无人机的航迹跟踪控制。除此之外,还有模型预测控制,H∞鲁棒控制,神经网络自适应控制,自适应模糊控制等[6-11]。

本文针对固定翼的小型无人机设计了相关的控制器来达到对飞行轨迹的准确跟踪。对于常规固定翼的小型无人机,其执行机构一般只有副翼舵、俯仰舵、偏航舵和推力装置,而无人机在三维空间的运动通常具有6个自由度,即独立控制变量的个数小于系统自由度的个数,所以固定翼无人机控制系统是典型的欠驱动控制系统。相比于完全驱动系统,欠驱动系统结构简单,便于进行整体的动力学分析和试验。但是由于系统的高度非线性、参数摄动、多目标控制要求及控制量受限等原因,欠驱动系统又足够的复杂。本文针对欠驱动系统提出了相关的控制方法。对于航迹跟踪问题,在给定飞行轨迹中选取一系列的航迹点,若能实现对飞行轨迹上的航迹点进行准确跟踪,则可认为能够对飞行轨迹进行跟踪。本文的控制思想可简单描述为:将无人机的速度坐标系对准航迹点所在的理想坐标系,通俗地讲,即控制无人机的速度方向指向航迹点,然后以一个理想速度去接近航迹点,根据该思想,无人机在有限的时间内一定能够到达航迹点所在的位置,从而实现对无人机航迹的跟踪。

1 系统建模

1.1 定义和相关说明

例:假设V1=[v1v2v3]T,则有

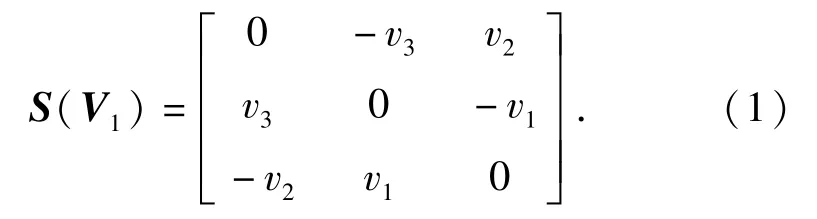
1.2 质心运动数学建模

根据文献[7],飞行器空中质心运动模型可表示为

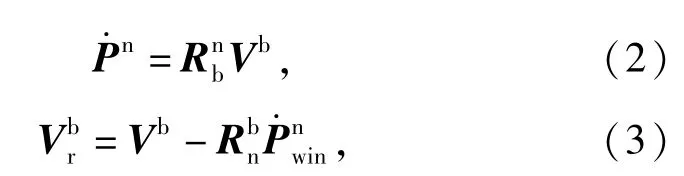
式中:Vb是飞行器质心的速度矢量;是机体速度;Vb相对于风速的相对速度;从机体系到速度坐标系的转换矩阵可表示为

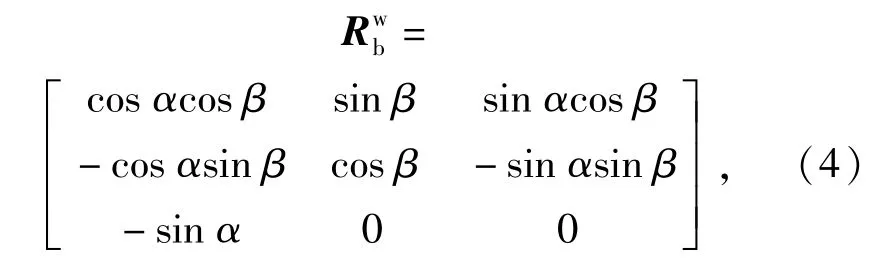
式中:攻角α和侧滑角β可分别表示为

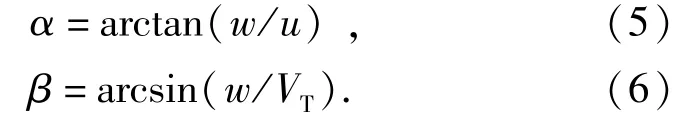
(6)式中:

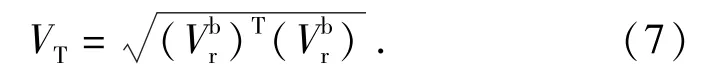
相对速度在速度坐标系下的投影可表示为

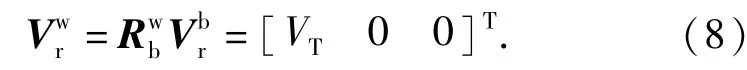
假设风速是常量或者变化很小,根据牛顿第二定律,机体系的相对加速度可表示为

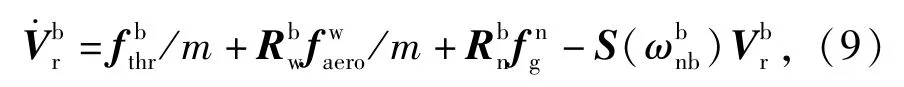
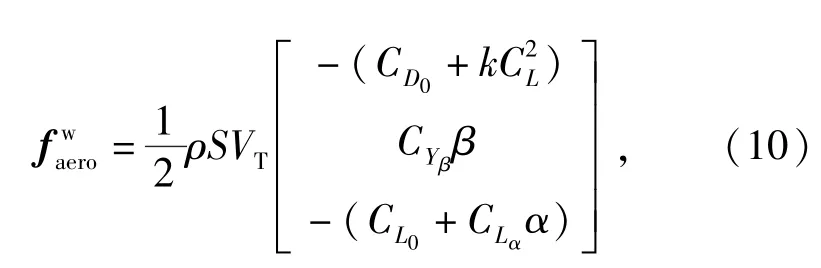
式中:ρ是空气密度;S是翼展面积;C(·)是气动力系数;CL=CL0+CLαα.

对(7)式求导,可得

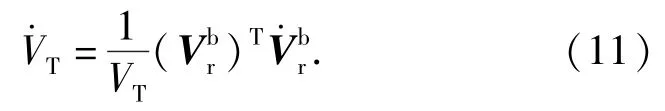
(9)式代入(11)式,可得

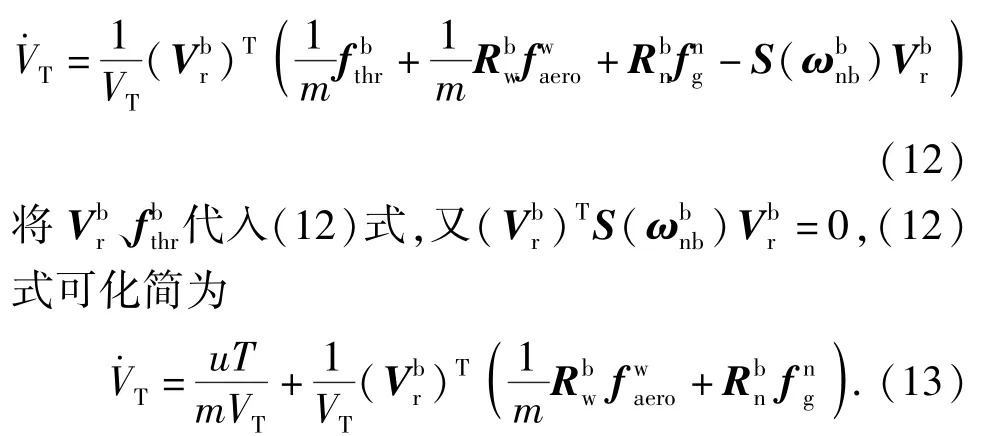
(13)式为速度变化的动力学模型,在后文设计速度控制器的时,只要通过改变推力的大小即可改变总速度的大小。

1.3 绕质心转动数学建模

本文利用机体系和地理系之间的转动四元数对无人机的姿态信息进行描述。单位四元数的数学模型可表示为

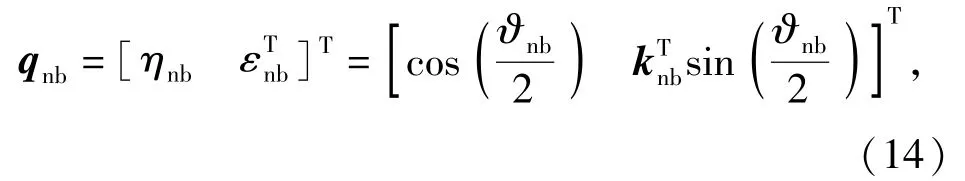
对姿态信息的描述同样还可以利用旋转矩阵进行描述,旋转矩阵(姿态矩阵)Rnb四元数之间的关系为

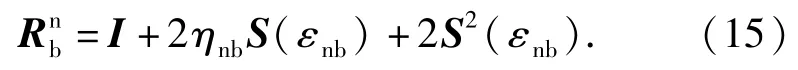
根据文献[3]基于四元数的转动动力学模型可表示为

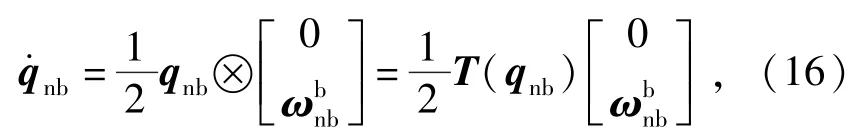
式中:

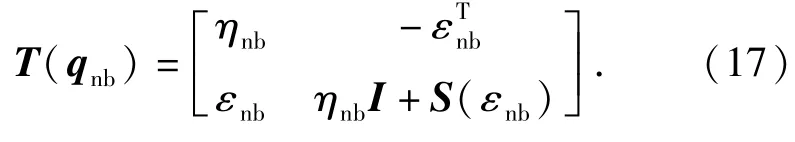
无人机角度动力学方程可以写为

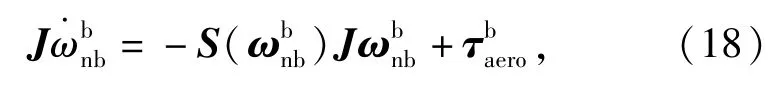
式中:

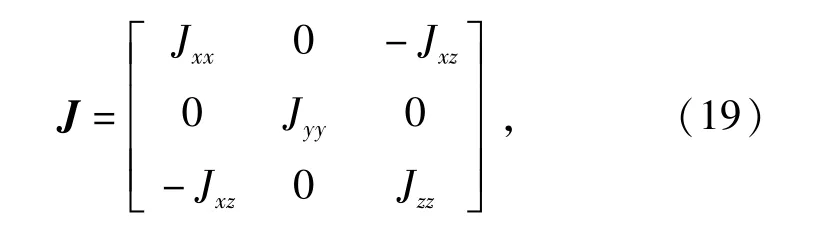
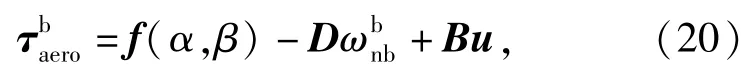
(20)式中u=[δaδeδr]T为飞行器的3个舵偏角,作为飞控系统的控制量。并有

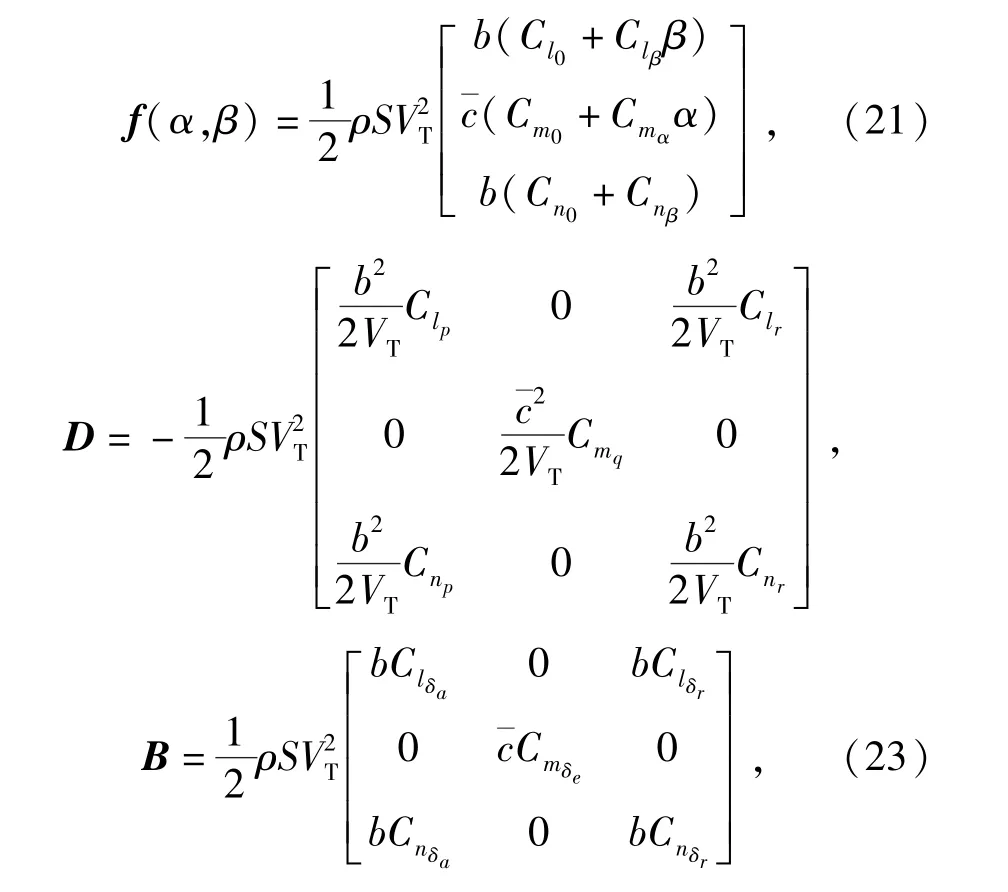
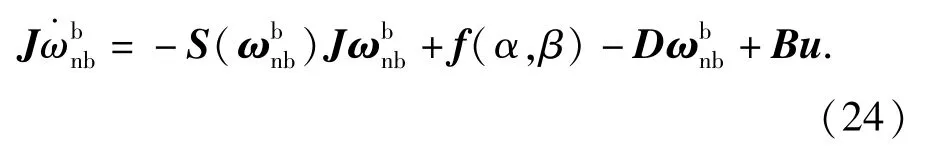
本文设计姿态控制器的目的是调整无人机的姿态信息使得其速度坐标系对准理想坐标系,理想坐标系是理想航迹点所在的坐标系,其定义及详细说明可见参考文献[9],定义速度坐标系和理想坐标系之间的转动四元数为qdw:

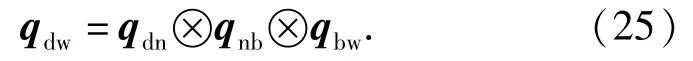
qdw有两个平衡点:这两个点虽然数学表达式不同,但具有完全相同的物理意义,即速度坐标系和理想坐标系的各个轴所指的方向完全相同,不需要任何转动就能使两个坐标系完全重合。根据文献[4],定义一个误差四元数:

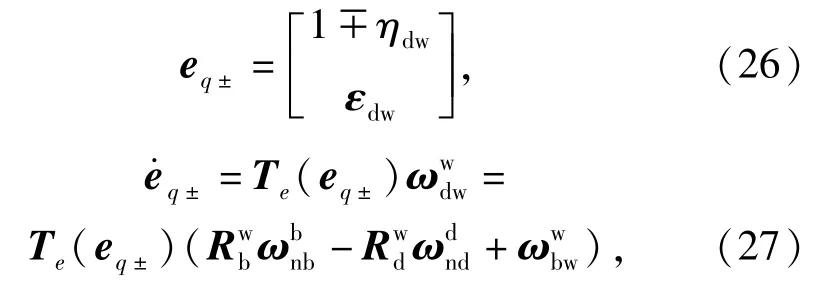
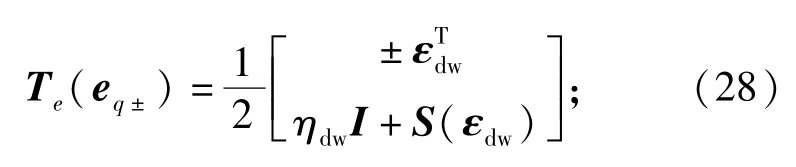
假设 ∀t,有sign(ηdw(t))=sign(ηdw(t)).该假设可以保证在推导控制器的过程中考虑任意一个平衡点其结果都是一样的。

引理 在假设1成立的情况下,下述不等式成立:

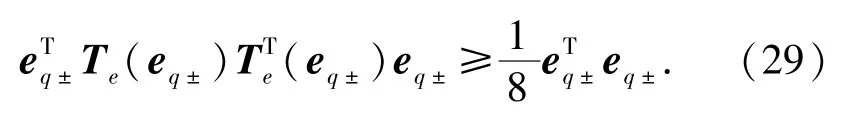
该证明过程详见参考文献[9-10]。

2 制导律设计

制导系统的目的是给后续的控制系统提供理想的参考信息。从本文整体的控制思路来讲,文中将位置误差投影到期望的姿态信息上,将速度误差投影到期望的角速度矢量上,所以推导出期望的姿态信息和期望的角速度信息是本节的任务。本文所述控制方法的基本思想是将位置和速度误差投影到Xd轴上,然后利用发动机推力使其到达预定航迹点。

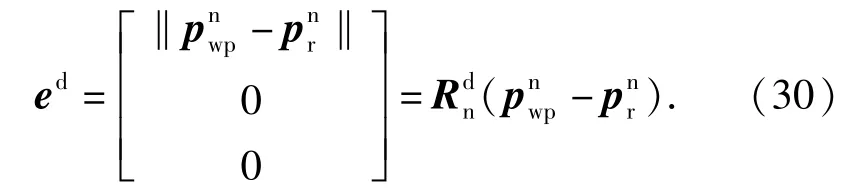
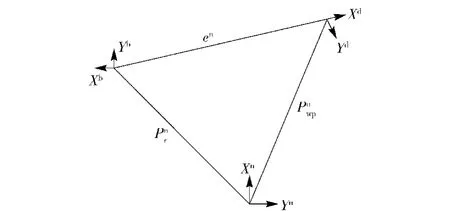
图1 地理坐标系、机体坐标系和理想坐标系的位置关系Fig.1 The relationship among geographic frame,body frame and desired frame

从(30)式可以看出:将地理坐标系中的位置误差投影到了理想期望的Xd轴上。定义建立地理系和理想坐标系之间的旋转四元数,根据四元数理论,其旋转角和旋转轴可分别表示为

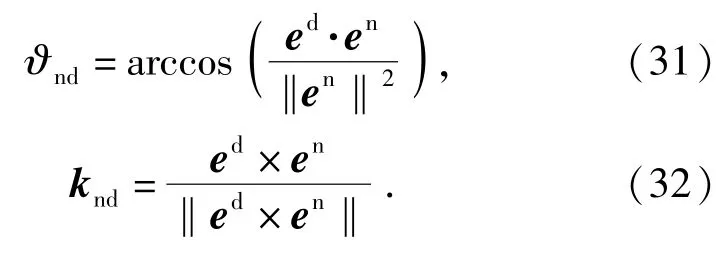
则期望的旋转四元数方程可以表示为

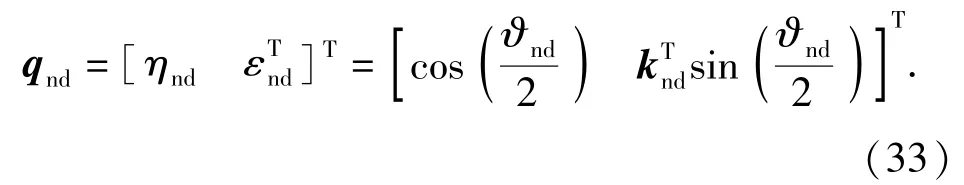
期望的旋转矩阵可表示为

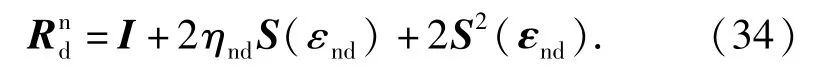
有了(33)式或(34)式,即可得到期望的姿态信息。

为了找到理想角速度,对(30)式求导,可推出:

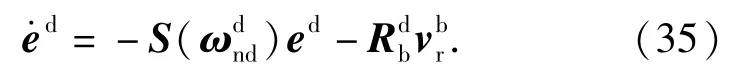
在理想坐标系中跟踪误差的导数亦可表示为

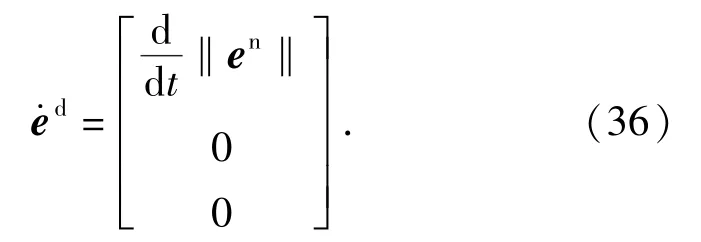
(36)式表明速度误差在Yd和Zd轴的分量为0.由于且

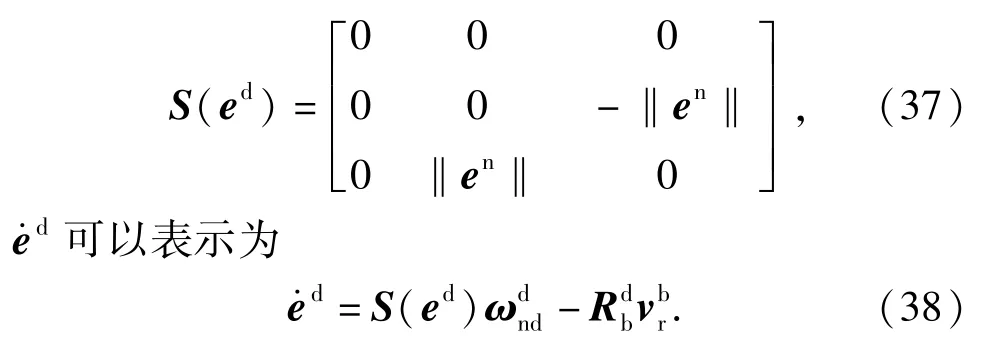
从(37)式可以看出,仅仅在Yd轴和Zd轴具有分量,其物理意义表明当求解理想角速度时,可以忽略Xd分量的值,且并不影响最终的结果。

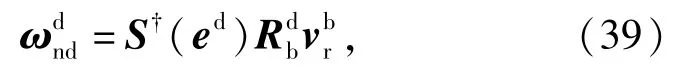
式中:†表示伪逆,且仅需要期望的俯仰和偏航角速度就能将速度指向期望的方向。通过对(39)式求导可以得到理想坐标系中的理想角加速度。如果无人机能够跟踪上述所推导的理想姿态、角速度和角加速度,那么跟踪误差就会投影到Xd轴上,且在推力矢量的作用下趋近于0,并穿梭在两个航迹点之间,从而实现对轨迹的动态跟踪控制。

3 速度控制器设计

在设计速度控制器的过程中,本文设计了反步控制器来对速度进行控制。记理想速度VTd＞0,速度误差为令VT-VTd,结合(13)式推导出

根据Lyapunov稳定性理论,(χ1,z)→(0,0),继而χ2→0,有 VT→VTd,从而实现了对速度的控制。

4 姿态控制器设计

本文设计姿态控制器的目的是,调整无人机的姿态使其速度矢量指向航迹点所在的位置。利用滑模变结构控制理论对姿态进行控制。为了不失一般性,设 eq=eq+,Te=Te(eq+).定义滑模面方程[12-13]为

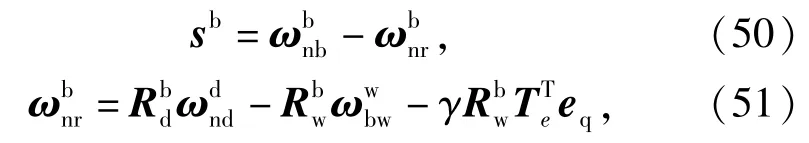
式中:sb是滑模变量;是参考坐标系相对于地理坐标系的转动角速度,该变量的引入可详见参考文献[14];γ是正增益系数。在(50)式左乘转动惯量矩阵J,并对其求导,将(24)式代入,又有可推导出

5 数值仿真

本文对无人机制导与控制系统进行了全系统仿真。仿真的初始条件;理想速度信息VTd=40 m/s;路径点矩阵选为

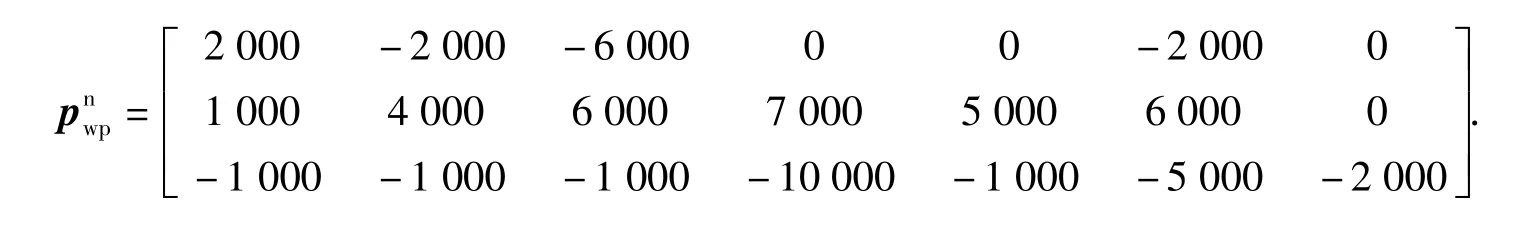
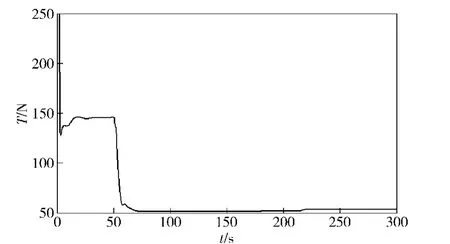
图2 推力变化趋势Fig.2 The change trend of thrust

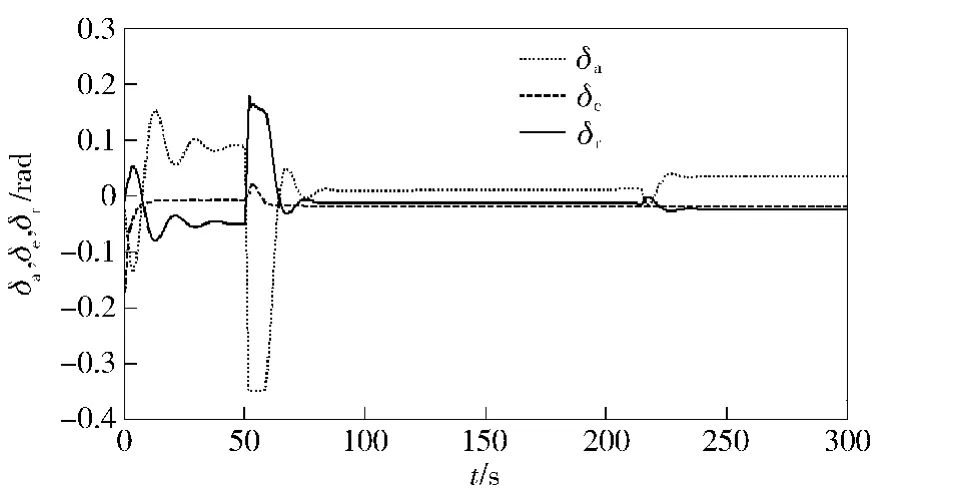
图3 3个舵偏角变化趋势Fig.3 The change trend of tree deflection angles

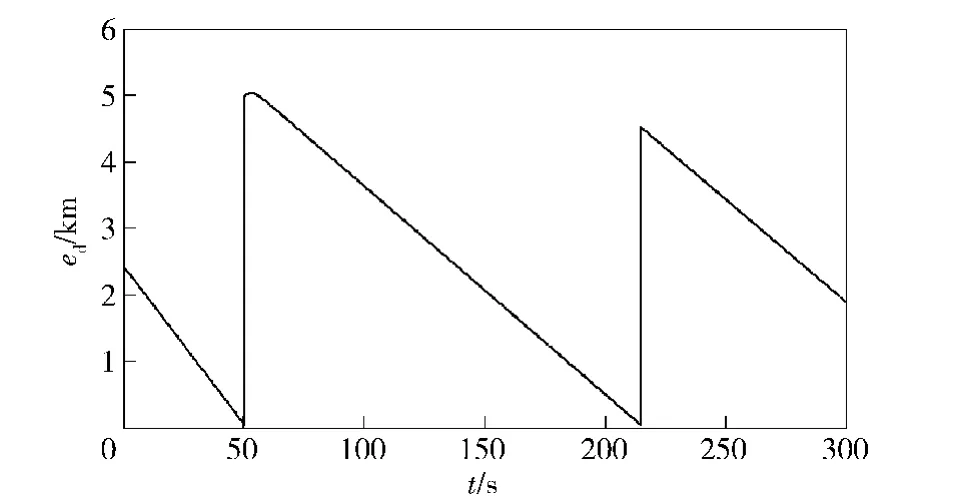
图4 位置跟踪误差Fig.4 The position tracking error

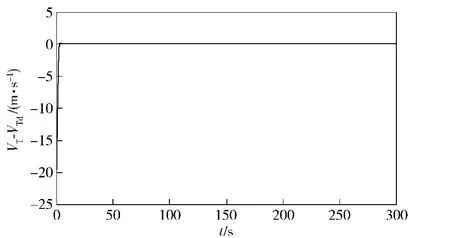
图5 速度跟踪误差Fig.5 The velocity tracking error

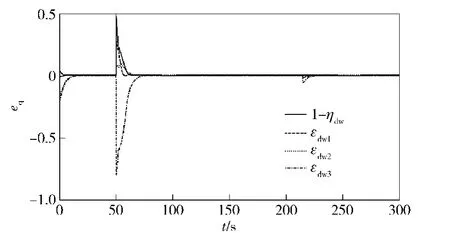
图6 角度跟踪误差Fig.6 The angle tracking error

当机体位置和路径点之间的距离小于5 m的时候切换到下一个参考点作为控制目标。图2和图3表示的是控制律随时间的变化关系,分别是推力T和舵偏角μ的变化曲线。图4和图5分别是位置ed和速度跟踪误差VT-VTd.分析图4的数据可以看出,在航迹点附近误差基本为0,即系统可以很好地跟踪目标航迹点。图6和图7分别是角度误差eq和角速度误差。从图6可以看出,角度误差很快收敛到0,大约在50 s左右的时候开始跟踪第一个航迹点,并大约在65 s左右时收敛到0,220 s左右的时候调整跟踪第二个航迹点,这时误差出现波动,但很快收敛到0.同理,角速度误差也表现出同样的特性。综上所述,本文所设计的控制器,跟踪精度较高,具有较强的鲁棒性,对实际工程应用和理论研究具有一定的参考价值。

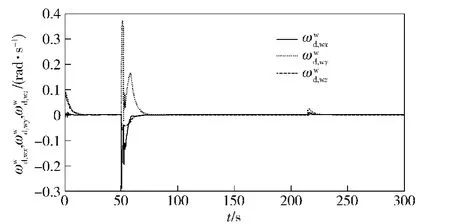
图7 角速度跟踪误差Fig.7 The angular velocity tracking error

6 结论

本文设计了无人机航迹跟踪控制器,基于路径点的轨迹跟踪,系统实现较简单,在工程实践中会表现出较大的优越性。针对于欠驱动系统,将不能被直接控制的状态量转化为其他可被直接控制的状态量,进而实现全状态控制。推导了制导律,基于Lyapunov稳定性理论设计了相关的控制器。仿真结果表明该系统具有较高的跟踪精度,具有较强的稳定性。

References)

[1]Enns D,Bugajski D,Hendrick R,et al.Dynamic invention-an evolving methodology for flight control design[J].International of Control,1994,59(1):71-91.

[2]Sieberling S,Chu Q P,Mulder J A.Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction[J].Jornal of Guidance,Control and Dynamics,2010,33(6):1732-1742.

[3]刘芳,陈万春.应用Lyapunov方法分析自旋导弹动态逆控制器鲁棒性[J].北京航空航天大学学报,2013,39(1):132-137.LIU Fang,CHEN Wan-chun.Spinning missile dynamic inversion controller robustness analysis using Lyapunov methods[J].Journal of Beijing University of Aeronautics and Astronautics,2013,39(1):132-137.(in Chinese)

[4]陶冶,房建成,盛蔚.一种小型无人机带死区增益PID自适应控制器设计与实现[J].自动化学报,2008,34(6):716-721.TAO Ye,FANG Jian-cheng,SHENG Wei.Design and realization of piecewise PID controller with dead zone for micro UAV[J].Acta AutomaticSinica,2008,34(6):716-721.(in Chinese)

[5]刘重,高晓光,符小卫,等.基于反步法和非线性动态逆的无人机三维航路跟踪制导控制[J].兵工学报,2014,35(12): 2030-2040.LIU Zhong,GAO Xiao-guang,FU Xiao-wei,et al.Three-dimensional path tracking guidance and control for unmanned aerial vehical based on back-stepping and nonlinear dynamic inversion[J].Acta Armamentarii,2014,35(12):2030-2040.(in Chinese)

[6]Khalil H K.Nonlinear systems[M].3rd ed.Upper Saddle River,NJ,US:Preentice Hall,2002.

[7]Wibowo S S.Aircraft flight dynamics control and simulation-using MATLAB and SIMULINK:cases and algorithm,apporach[M].Kuala Lumpur,Malaysia:University of Kuala Lumpur-Malaysian Institute of Aviation Technology,2007.

[8]Egeland O,Gravdahl J T.Modeling and simulation for automatic control[M].Norwegian:Marine Cybernetics,2002.

[9]Kristiansen R.Dynamic synchronization of spacecraft-modeling and coordinated control of leader-follower spacecraft formations [D].Norwegian:Norwegian University of Science and Technology,2008.

[10]Oland E,Kristiansen R.Adapative flight control with constrained actuation[C]//2014 American Control Conference.Portland,Oregon,US:the American Automatic Control Council,2014.

[11]Oland E,Schlanbusch R.Underactuated way point tracking of a fixed-wing UAV[C]//Proceedings of the 2nd IFAC Workshop on Research,Education and Development of Unmanned Aerial Systems.Compiegne,France:IFAC,2013.

[12]Shima T.Sliding-mode control for integrated missile autopilot guidance[J].Journal of Guidance,Control,and Dynamics,2006,29(2):250-260.

[13]Roberts A,Tayebi A.Adaptive position tracking of VTOL UAVs [J].IEEE Transactions on Robotics,2011,27(1):129-142.

[14]Slotine J E,Li W.Adaptive manipulator control:a case study [J].IEEE Transaction on Automatic Control,1998,33(11): 995-1003.

Study of Flight Path Tracking and Control of an UAV in 3D Space

GUAN Jun1,YI Wen-jun1,CHANG Si-jiang2,LIANG Zhen-dong1,LYU Yi-pin1
(1.National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China; 2.School of Power and Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

A flight path tracking problem is studied for underactuated UAV in 3D space.The question of flight path tracking is transformed into way-point tracking by choosing a serious point on flight path.A mathematic model is established.The speed frame is alined to the desired frame so that position tracking is converted into attitude tracking.The guidance law is also deduced,and the theories of sliding variable structure and back-stepping are used to design the attitude controller and velocity controller.The direction of velocity vector is aligned to the position of a way-point by using the attitude controller.The speed of UAV is controlled by the velocity controller to make the UAV closing to a way-point.The guidance and control systems are simulated.The result shows that the designed controller is perfect in tracking and have a strong robustness.

control science and technology;back-stepping;sliding variable structure;UAV;flight path tracking;Lyapunov function

V249.1

A

1000-1093(2016)01-0064-07

2015-04-16

国家自然科学基金项目(11472136、11402117);江苏省普通高校研究生科研创新计划项目(KYLX15-0419)

管军(1987—),男,博士研究生。E-mail:guanjun8710@163.com;易文俊(1970—),男,教授,博士生导师。E-mail:wjy@mail.njust.edu.cn