斜拉桥锚拉板足尺模型疲劳试验
2016-11-09王连华丁秉昊李立峰
王连华++丁秉昊++李立峰

摘要:为研究斜拉桥钢主梁与锚拉板采用对接焊形成的“上”字形索梁锚固结构的疲劳性能,进行了锚拉板足尺模型疲劳试验。通过全桥有限元分析确定了疲劳试验的模型设计;综合对比多种疲劳荷载计算方法,确定了试验的疲劳荷载;考虑平均应力对疲劳荷载的影响,确定了疲劳荷载的最大、最小峰值。结果表明:足尺模型历经300万次疲劳加载后,各部位均未发现疲劳裂纹,应力测试结果与有限元分析值吻合良好;“上”字形索梁锚固结构的疲劳性能满足工程要求。
关键词:斜拉桥;锚拉板;足尺试验;疲劳性能;疲劳荷载;平均应力
中图分类号:U448.27 文献标志码:A
0 引 言
锚拉板结构作为钢混叠合梁斜拉桥中常见的一种索梁锚固体系,通常由锚拉板、加劲板、锚拉筒、承压板及加强板组成[16],具有构造简单、传力明确、便于安装和日常检修维护的特点,应用较为广泛。传统的锚拉板结构通常与钢主梁顶板直接焊接,锚拉板与钢主梁顶板的焊缝验算属于单边V形坡口焊,如湛江海湾大桥、丰都长江二桥、厦漳跨海大桥等。各国对这种传统形式的锚拉板式锚固结构研究相对完善,任伟平等[7]通过湛江海湾大桥锚拉板足尺试验,对锚拉板的结构特点、制造工艺、传力机理进行了研究;骆炜然[8]通过丰都长江二桥锚拉板足尺疲劳试验,探讨了传统形式锚拉板疲劳试验的试验方法;姚建军等[1]对厦漳跨海大桥锚拉板结构进行了受力计算,分析了锚拉板主要构件尺寸、厚度等参数对结构受力的影响;孟云[9]对江津观音岩长江大桥锚拉板采用1∶4缩尺模型分析了其静力与疲劳性能。上述试验研究表明,对于传统形式的锚拉板结构,锚拉板与锚拉筒焊接圆弧处存在应力极值,锚拉板与钢主梁顶板焊缝内侧圆弧过渡处有应力集中,也是疲劳可靠性的验证重点。关于锚拉板与主梁腹板采用对接焊缝形成的“上”字形索梁锚固结构疲劳性能的理论分析和试验研究相对较少,有必要开展相关研究,探究其疲劳性能。
1 试验概况
1.1 模型设计
拟建于贵州省内的乌江大桥主桥为一座主跨360 m的双塔双索面混合式叠合梁斜拉桥,全长610 m。主跨钢主梁采用“上”字形截面,主梁腹板高出主梁顶板20 mm,主梁与锚拉板焊接处高出主梁顶板120 mm,锚拉板与边主梁腹板顶缘之间采用对接焊缝连接,乌江大桥锚拉板示意如图1所示,其中t为板件厚度。相比传统形式锚拉板,受力必定有所不同。因此,为确保本桥锚拉板与主梁腹板对接焊缝的疲劳可靠性,对该种锚拉板形式设计足尺模型进行疲劳试验,验证其可靠性。
运用MIDAS/Civil建立全桥有限元模型(图2),静力分析表明,拉索M14处索力值最大;得到每根拉索影响线后,分别按照《公路桥涵设计通用规范》(JTG D60—2015)公路Ⅰ级荷载加载,计算对比得拉索M14索力增量最大,大小为640 kN。综合考虑得出,此处锚拉板受力最不利,容易发生疲劳破坏,因此本文选取拉索M14处锚拉板结构进行研究,依据实桥锚拉板的尺寸制作试验模型。疲劳试验以足尺最佳,选定模型相似比为1∶1。通过有限元试算对比,最终试验模型边主梁尺寸为8.2 m×0.8 m×1.7 m,腹板厚40 mm,锚拉板厚50 mm,边主梁截面布置和长度以不影响结构疲劳受力为原则进行适当简化。乌江大桥试验模型的锚拉板构造、关键测点布置和边主梁截面形式如图1所示,试验模型的制造与实桥结构一致,焊接工艺相同。模型出场前进行无损探伤检测,没有发现焊接裂缝。
1.2 疲劳荷载幅确定
对于锚拉板疲劳试验,首先需要确定锚拉板承受的疲劳荷载大小。本文对比《公路钢结构桥梁设计规范》(JTG D64—2015)[10]、美国AASHTO规范[11]和英国BS 5400规范[12]以及中国现有锚拉板疲劳试验荷载确定方法计算得到的疲劳荷载,最终确定本文疲劳试验的加载模式。
1.2.1 按照《公路钢结构桥梁设计规范》计算
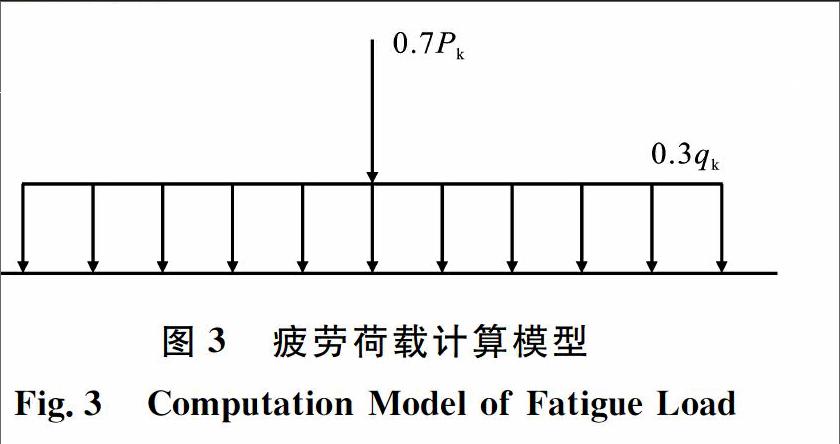
《公路钢结构桥梁设计规范》(JTG D64—2015)规定,疲劳荷载计算模型采用等效的车道荷载(图3),集中荷载为0.7Pk,均布荷载为0.3qk,Pk和qk分别为集中荷载标准值和均布荷载标准值,按公路Ⅰ级车道荷载标准取值;应考虑多车道的影响,横向车道折减系数应按现行《公路桥涵设计通用规范》的相关规定选取。
采用影响线加载,按照《公路钢结构桥梁设计规范》规定,采用等效车道荷载对拉索M14影响线进行最不利加载,计算得出等效车道荷载下拉索M14的索力增量为212.2 kN。
1.2.2 按照AASHTO规范计算
按照AASHTO规范规定,取一辆325 kN标准疲劳车分别加载在6个车道,得到各车道下拉索M14的轴力历程,根据每条索的轴力历程,采用雨流法算出索力值[13],结果如表1所示。
乌江大桥的设计寿命为120年,其设计交通量偏安全取6车道高速公路平均车速80 km·h-1的最大日交通量上限值ADT=60 000 veh·d-1[14],认为桥梁建成即达到饱和交通量。根据AASHTO规范,单车道日平均货车交通量ASL为
ASL=pA
(1)
式中:p为单车道货车交通量所占的比例,3车道及以上取为0.8;A为设计寿命期限内平均每天的单车道货车数,A=kADT/2=6 000 veh·d-1,k为货车占总交通量的比例,按照AASHTO规定,货车在交通量中所占比例为0.1~0.2,本文保守取为0.2。
通过计算可得ASL=4 800 veh·d-1。对应的单车道应力循环次数N=210 240 000,则相应各车道的换算荷载循环次数Ni为
Ni=C5iN
(2)
将表1中Ci代入式(2),6车道总等效循环次数NT=677 231 849。根据Miner线性累积损伤理论,以49.08 kN作为疲劳荷载,循环677 231 849次没有破坏即认为结构满足疲劳强度要求。
进行200万次循环的荷载换算倍数n=(677 231 8492 000 000)13=6.97,动荷载冲击系数取0.15,考虑冲击叠加作用的动荷载冲击系数为1.15,则疲劳荷载幅ΔP=6.97×1.15×49.08 kN≈393 kN。
1.2.3 按照BS 5400规范计算
按照BS 5400规范的规定,标准疲劳车重为320 kN,疲劳车辆只布置在慢车道及相邻车道上,且相邻车道与慢车道的年交通量比例为1.5∶2=0.75。因此,对于乌江大桥车道1,6的循环次数为210 240 000,同样可以求得车道2,5的循环次数为0.75×210 240 000=157 680 000,则总的循环次数为
NT=KF∑C5iN
(3)
式中:KF为应力修正系数。
根据BS 5400规范,影响线长度L>200 m时,KF=2.95,则NT=1 306 906 312。
同上,换算倍数n=(1 306 906 3122 000 000)13=8.678,则ΔP=8.678×49.08 kN=426 kN。
1.2.4 中国通用做法
调研中国已有斜拉桥锚拉板疲劳试验,疲劳荷载幅一般取50%~60%活载下最大索力增量。根据整体分析,公路Ⅰ级荷载下中跨尾索的索力增量为640 kN,其60%的索力增量为384 kN。
对比上述4种疲劳荷载幅计算方法,按照BS 5400规范计算所得疲劳荷载幅最大,更为保守,故为方便加载,本文试验疲劳荷载幅取为450 kN。
1.2.5 考虑平均应力的影响
对于疲劳试验,确定合理的试验应力幅对于疲劳试验非常重要。反映材料疲劳性能的疲劳强度疲劳寿命曲线(SN曲线)是在给定应力比R下得到的,R=-1对称循环时的SN曲线是基本SN曲线。通常情况下,规范给定的SN曲线均是基本SN曲线。在给定寿命N下,研究循环应力幅Sa与平均应力Sm的关系可知,平均应力Sm越大,对应的应力幅Sa越小,但均不会大于材料极限强度Su。对SaSm曲线拟合,可得Sa/S-1+Sm/Su=1(其中,S-1为R=-1时材料的疲劳极限,Su为材料的极限强度),即Goodman直线(图4)[1516]。
乌江大桥拉索M14在服役状态下的索力范围为5 184~5 634 kN,试验模型有限元分析中将索力直接加在相应位置,得到疲劳荷载作用下乌江大桥锚拉板控制点的循环应力最大值Smax和最小值Smin,从而计算出对应的应力幅Sa和平均应力Sm,代入Goodman直线方程求出相应的S-1,记为S1。实际疲劳试验中疲劳荷载最小值Pmin=67 kN,最大值Pmax=517 kN,同样运用有限元分析计算出对应的Sa和Sm,按照Goodman直线方程计算出其对应的S-1,记为S2。
遵循损伤等效原则,n1/N1=n2/N2,则n1/n2=N1/N2=(S1/S2)m。目前中国疲劳试验的通用加载次数为200万次,即认为按照实际疲劳应力幅循环200万次产生的疲劳损伤与实桥120年内的疲劳累积损伤相等,故n1=2×107,从而可得n2=2.32×107。因此,按照试验荷载Pmin=67 kN,Pmax=517 kN进行循环加载232万次产生的损伤与实桥120年内疲劳车通过产生的损伤相等,故疲劳试验加载次数、疲劳荷载的确定均需考虑平均应力的影响。
综上分析,本文疲劳试验的动载加载幅值为450 kN,其中Pmin=67 kN,Pmax=517 kN。
1.3 试验方案
1.3.1 试验系统
在实桥结构中边主梁水平放置,拉索M14中心线与水平方向成27.183°。如果试验模型按照实桥中锚拉板的方位摆放,疲劳机需要模拟拉索施加斜向拉力,这种试验形式不利于疲劳加载。为方便试验加载,将钢主梁斜置,保证斜拉索中心线竖直向下。钢主梁一端锚固在地面上,一端采用工字钢做立柱支撑。另外设计加载横梁系统,加载横梁中部开孔与锚拉筒用钢绞线锚固,并以钢绞线模拟斜拉索传递拉力,且加载横梁一端铰支,另一端放置疲劳机作动器利用杠杆原理进行加载。疲劳试验总体布置、加载装置及试验现场如图5所示。
1.3.2 试验工况
加载系统就位后,首先采用电液式脉动疲劳机预加载67 kN静力后卸载,消除加载系统之间的间隙,然后按照Pmin=67 kN,Pmax=517 kN进行疲劳加载,加载频率为2.0 Hz。试验模型经历0次、50万次、100万次、150万次、200万次、250万次、300万次疲劳加载后均停机进行静载测试。静力测试采用逐级加载的方式,每级增量为90 kN,依次记录每个荷载工况下各测点的应变值。2 有限元分析
2.1 模型建立
为保证试验模型能反映实桥结构受力特征,并对试验模型的应力分布情况有全面的了解,增强试验针对性,采用有限元软件ANSYS对试验模型进行有限元分析[1718],有限元模型如图6所示。钢结构板件均采用壳单元Shell181模拟,弹性模量取2.06×105 MPa,立柱和主梁底部均采用固接约束,荷载取上峰值517 kN垂直于锚垫板均布加载,以模拟斜拉索的拉力[1920]。
2.2 有限元计算
选取试验模型锚拉板进行分析,得到如图7所示的等效应力云图。由图7可知:锚拉板与锚拉筒连接焊缝圆弧过渡处存在应力集中,最大等效应力为50.34 MPa;锚拉板其他位置等效应力偏低,在10 MPa左右,由上往下随拉板宽度增大而减小;锚拉板与主梁腹板焊缝最大等效应力出现在内侧圆弧过渡处,为16.47 MPa。
本文试验采用足尺模型,测点较多,仅列举部分关键区域测点数据,对关键测点等效应力进行对比,结果见表2。
对比得出,有限元计算值与试验测量值最大等效应力均出现在锚拉板与锚拉筒连接焊缝圆弧过渡处(测点A51),锚拉板与边主梁腹板对接焊缝处最大等效应力都出现在内侧圆弧过渡处(测点A26),有限元计算值与试验测量值吻合较好。3 疲劳试验结果分析
3.1 疲劳幅值为450 kN
按照疲劳幅值为450 kN加载200万次后,开展静力加载试验,测试应力结果分析表明:5次静载数据显示锚拉板的最大等效应力为37.21 MPa,出现在锚拉板与锚拉筒圆弧过渡处(测点A51),与有限元分析位置一致;随着垂直斜拉索中心线方向锚拉板面积增大,锚拉板中下部应力水平降低,大部分测点应力在10 MPa左右;锚拉板与主梁腹板对接焊缝整体应力较低,但在内侧圆弧过渡处(测点A26)出现应力集中,等效应力为19.35 MPa,主拉应力为22.28 MPa;4个测点等效应力和静力荷载呈线性关系(图8),结构处于弹性工作阶段。
3.2 疲劳幅值为640 kN
200万次加载结束后,为探究结构处于超长服役期内的疲劳性能,增大疲劳幅值为640 kN,加载至300万次。加载结束后测得517 kN静载作用下的应力数据与疲劳试验前数据的对比见表3,测点应力变化不大,试验模型焊缝部位没有疲劳裂纹出现,表明结构的疲劳性能可靠。
次加载后测点在静载作用下的应力。4 疲劳验算
中国《公路钢结构桥梁设计规范》(JTG D64—2015)、美国AASHTO规范和英国BS 5400规范均针对各种典型的焊接或者非焊接连接细节给出了对应的疲劳容许应力,因此可按照相关规范来验算锚拉板与主梁腹板对接焊缝的疲劳可靠性,该焊缝最大主拉应力取测点A26处主拉应力22.28 MPa。
按照《公路钢结构桥梁设计规范》验算,锚拉板与主梁腹板焊缝为两板中心对齐的不同厚度横向对接焊缝,此类构造细节的常幅疲劳临界值σ=70.0 MPa>22.28 MPa,故该构造疲劳可靠性满足《公路钢结构桥梁设计规范》要求。
按照AASHTO验算,锚拉板与主梁腹板对接焊缝的构造细节等级属于C类,此类构造细节的常幅疲劳临界值σ=69.0 MPa>22.28 MPa,因此该构造疲劳可靠性满足美国AASHTO要求。
按照BS 5400验算,锚拉板与主梁腹板对接焊缝的构造细节等级属于E类[21],此类构造细节的常幅疲劳临界值σ=80.41 MPa>22.28 MPa,所以该构造疲劳可靠性满足BS 5400要求。5 结 语
(1)对比4种对疲劳荷载幅的确定方法,结果表明按照BS 5400计算所得疲劳荷载幅值最大,最为保守。疲劳试验荷载的确定应综合考虑各国相关规范、试验研究成果及平均应力的影响。
(2)有限元分析与试验结果均表明,锚拉板与主梁腹板对接焊缝区域应力水平较低且分布均匀,采用锚拉板与主梁腹板对接焊形成的“上”字形索梁锚固构造较合理,可为同类工程设计提供参考。
(3)乌江大桥锚拉板足尺模型历经300万次疲劳试验加载后,钢结构和焊接细节均未出现疲劳开裂现象。疲劳试验表明,“上”字形索梁锚固结构疲劳性能良好,满足工程要求。
参考文献:
References:
[1] 姚建军,李 军.厦漳跨海大桥北汊主桥锚拉板锚下区域受力分析[J].桥梁建设,2013,43(4):3943.
YAO Jianjun,LI Jun.Force Condition Analysis of Zone Under Anchor Tensile Plate of North Main Bridge of Xiazhang Seacrossing Bridge[J].Bridge Construction,2013,43(4):3943.
[2]朱劲松,肖汝诚,曹一山.杭州湾跨海大桥索梁锚固节点模型试验研究[J].土木工程学报,2007,40(1):4953,59.
ZHU Jinsong,XIAO Rucheng,CAO Yishan.Model Test on the Cable Anchorage of the Main Girder of the Hangzhou Bay Bridge[J].China Civil Engineering Journal,2007,40(1):4953,59.
[3]刘庆宽,王新敏,强士中.南京长江二桥南汊桥索梁锚固足尺模型试验研究[J].土木工程学报,2001,34(2):5054.
LIU Qingkuan,WANG Xinmin,QIANG Shizhong.Full Scale Model Test on Anchorage Zone of the Second Yangtze River Bridge at Nanjing[J].China Civil Engineering Journal,2001,34(2):5054.
[4]刘小渝,刘秀伟.斜拉桥钢锚拉板区域焊接应力消除试验研究[J].公路交通科技,2008,25(11):8286,91.
LIU Xiaoyu,LIU Xiuwei.Experimental Study on Releasing Welding Residual Stress in Steel Tensile Anchor Plate Area of Cablestayed Bridges[J].Journal of Highway and Transportation Research and Development, 2008,25(11):8286,91.
[5]夏培华,张若钢.斜拉桥锚拉板空间有限元分析与模型试验[J].中外公路,2012,32(6):181184.
XIA Peihua,ZHANG Ruogang.Spatial Finite Element Analysis and Model Test of Tensile Anchor Plate in Cablestayed Bridge[J].Journal of China & Foreign Highway,2012,32(6):181184.
[6]曾永平,陈克坚,袁 明,等.双锚拉板锚箱索梁锚固结构设计研究及疲劳试验[J].桥梁建设,2013,43(6):4550.
ZENG Yongping,CHEN Kejian,YUAN Ming,et al.Design Study and Fatigue Test of Cabletogirder Anchorage Structure of Double Tensile Anchor Plates and Anchor Box[J].Bridge Construction,2013,43(6):4550.
[7]任伟平,强士中,李小珍,等.斜拉桥锚拉板式索梁锚固结构传力机理及疲劳可靠性研究[J].土木工程学报,2006,39(10):6873,91.
REN Weiping,QIANG Shizhong,LI Xiaozhen,et al.Mechanical Behavior and Fatigue Reliability of Tensile Anchor Plate Structure in the Cablebeam Anchorage Zones of Cablestayed Bridges[J].China Civil Engineering Journal,2006,39(10):6873,91.
[8]骆炜然.斜拉桥索梁锚固区疲劳性能试验与研究[D].成都:西南交通大学,2013.
LUO Weiran.Tests and Research About Fatigue Property of the Cablegirder Connection for Cable Stayed Bridge[D].Chengdu:Southwest Jiaotong University,2013.
[9]孟 云.斜拉桥锚拉板式的锚固结构模型试验与研究[D].重庆:重庆交通大学,2009.
MENG Yun.Model Test on the Cablebeam Anchorage Structure with Tensile Anchor Plate of Cablestayed Bridges[D].Chongqing:Chongqing Jiaotong University,2009.
[10]JTG D64—2015,公路钢结构桥梁设计规范[S].
JTG D64—2015,Specifications for Design of Highway Steel Bridge[S].
[11]AASHTO,LRFD Bridge Design Specifications[S].
[12]BS 5400101980,Steel,Concrete and Composite Bridges.Part 10:Code of Practice for Fatigue[S].
[13]郑万山,唐光武,郑 罡.大跨度斜拉桥拉索疲劳参数分析中移动荷载的选定[J].公路交通技术,2010(5):5255.
ZHENG Wanshan,TANG Guangwu,ZHENG Gang.Selection of Moving Loads in Design of Cable Fatigue Parameters in Largespan Cablestayed Bridge[J].Technology of Highway and Transport,2010(5):5255.
[14]JTG B01—2003,公路工程技术标准[S].
JTG B01—2003,Technical Standard of Highway Engineering[S].
[15]SCHILLING C G.Stress Cycles for Fatigue Design of Steel Bridges[J].Journal of Structural Engineering,1984,110(6):12221234.
[16]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社,2002.
CHEN Chuanyao.Fatigue and Fracture[M].Wuhan:Huazhong University of Science & Technology Press,2002.
[17]李立峰,王连华.ANSYS土木工程实例详解[M].北京:人民邮电出版社,2015.
LI Lifeng,WANG Lianhua.Civil Engineering Example Explanation by ANSYS[M].Beijing:Posts & Telecom Press,2015.
[18]李立峰,张东波,袁卓亚,等.正交异性钢桥面板中弧形缺口的受力分析[J].公路交通科技,2012,29(4):5561.
LI Lifeng,ZHANG Dongbo,YUAN Zhuoya,et al.Stress Analysis of Arcshaped Cutouts in Steel Orthotropic Deck Plates[J].Journal of Highway and Transportation Research and Development,2012,29(4):5561.
[19]LERTSIMA C,CHAISOMPHOB T,YAMAGUCHI E.Threedimensional Finite Element Modeling of a Longspan Cablestayed Bridge for Local Stress Analysis[J].Structural Engineering and Mechanics,2004,18(1):113124.
[20]JAYARAMAN H B,KNUDSON W C.A Curved Element for the Analysis of Cable Structures[J].Computers & Structures,1981,14(3/4):325333.
[21]BS 540010C1980,Steel,Concrete and Composite Bridges.Part 10:Charts for Classification of Details for Fatigue[S].
