斜拉桥单向预应力体系索塔锚固区足尺模型试验研究
2016-06-07崔楠楠贾布裕余晓琳麦梓浩杨铮颜
崔楠楠+贾布裕+余晓琳+麦梓浩+杨铮+颜全胜
摘 要:为研究布置单向预应力的混凝土索塔锚固区的传力机理,明确该类新型索塔锚固区的实际受力状况,以广中江高速公路西江水道桥为工程背景,进行了索塔节段足尺模型试验和有限元数值分析,试验中特制了与实桥一致的平行钢丝索短索,并设计了斜向加载反力梁,以模拟斜拉索的大吨位斜向荷载;试验过程中观测结构的应力、变形以及裂缝发展.研究结果表明:理论分析与试验结果吻合较好,结构在1.2倍设计荷载下仍处在弹性受力状态,主要受力部位未发现裂缝;推算抗裂安全系数为2.04,布置在顺桥向塔壁的单向预应力能够提供足够的压应力储备.
关键词:斜拉桥;预应力混凝土;试验研究;索塔锚固区;单向预应力;有限元分析
中图分类号:TU378 文献标识码:A
文章编号:1674-2974(2016)05-0061-09
Abstract: In order to study the mechanism of new one-way pre-stressed tendons applied to cable-pylon anchorage zone, as well as to clarify the actual stress distribution of the tendons, a full-scale model test and finite element analysis were conducted. As the construction background, Xijiang River Bridge of Guangzhou - Zhongshan - Jiangmen highway was considered. To simulate the large-tonnage inclined load of the cable, four short parallel wire cables and a reaction beam were designed and manufactured. Strains, displacements, and cracks of the structure were measured. The predictions by the finite element analysis agreed well with the test results. The linear strain distributions of the structure were measured even at 1.2 times of designed load, and cracks did not occur in the main load-resisting members. In addition, the safety coefficient 2.04 was estimated to prevent cracks, and enough prestress reserve was provided by the one-way pre-stressed tendons placed in the longitudinal direction wall.
Key words:cable-stayed bridge; prestressed concredte; experiments; pylon anchorage zone; one-way prestressing tendons; FEA
斜拉桥索塔锚固区应力集中且分布复杂,是关系到斜拉桥结构安全的关键部位.对于斜拉索侧壁锚固的箱型截面混凝土索塔,目前大多采用U型、井型或混合型预应力布置形式,但其普遍存在施工困难,永存预应力不能保障以及预压应力与斜拉索产生的应力分布不吻合等缺陷[[1-3[];且U型预应力的摩阻损失规律难以掌握,其形状使得锚固区应力场更加复杂,在我国几乎每一座采用此种型式的大跨度斜拉桥都要进行模型试验,造成极大的浪费.为避免上述缺陷,提出一种新型的单向预应力布置形式,仅在顺桥向塔壁布置单向预应力,横桥向依靠厚壁混凝土抗剪来抵抗斜拉索水平分力.这种单向布束方式具有受力明确、施工简单等显著优点,广中江高速公路三座大跨度斜拉桥均将采用此方案,然而目前国内外鲜有类似案例,缺乏设计和施工经验,因此有必要通过模型试验研究其受力性能.
在相关试验研究方面,文献[4-5]中采用水平加载的方式进行足尺模型试验,研究了U型预应力锚固区的受力性能;文献[6]采用斜向加载的试验方式研究了井型预应力锚固区的受力性能;文献[7-9]采用斜向加载的方式对U型或混合型预应力锚固区进行了研究.文献[10-11]进一步对锚固区的受力机理和设计方法进行了研究.可以看出,目前国内外已积累了多个实际斜拉桥锚固区足尺模型试验的可靠数据,但试验结果往往仅适用于该相关工程,而且部分采用水平加载,与实际不符,斜向加载时用钢绞线代替平行钢丝索,导致索孔尺寸加大,削弱了结构;并且对于单向预应力布置形式的索塔尚未见相关研究,初步有限元分析表明,其受力模式以及开裂敏感区的位置与传统预应力布置形式的混凝土索塔有所不同.因此,本文针对这种新型的单向预应力体系索塔锚固区进行了足尺模型试验,试验中定制与实桥一致的短束平行钢丝索,采用实际角度的斜向加载,结合有限元分析,研究了不同荷载阶段下结构的应力,变形和裂缝发展情况,为单向预应力体系索塔锚固区的设计和施工提供依据.
本文依托工程为广中江高速公路西江水道桥,该桥为独柱双塔中央索面半飘浮体系斜拉桥,跨径布置为57.5 m+172.5 m+400 m+172.5 m+57.5 m.
1 足尺模型试验方案
1.1 试验节段选取与模型设计
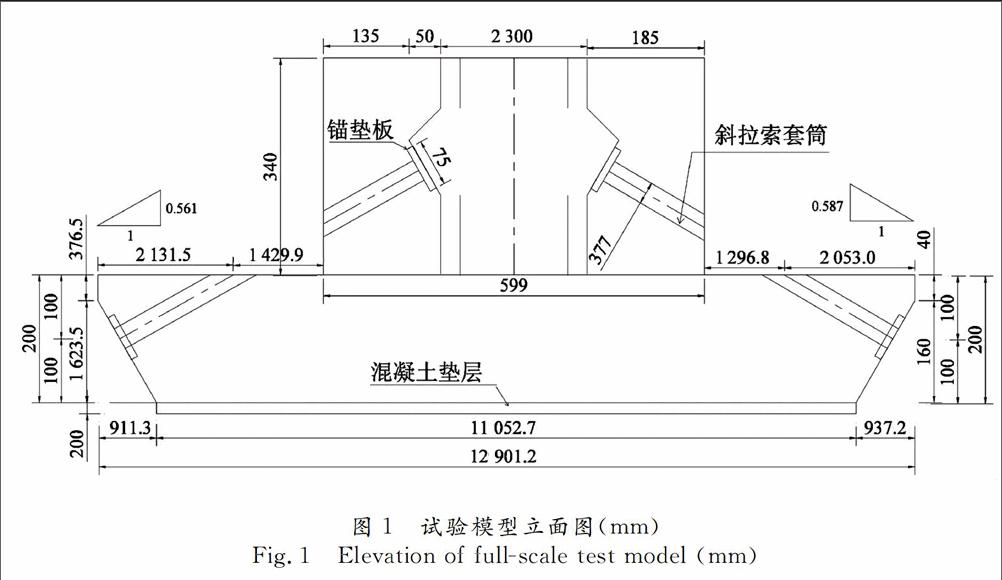
西江水道桥索塔采用“方圆结合”造型,整个索塔由底部的正方形截面逐渐变化到顶部的圆形截面.通过建立整个桥塔的有限元模型,得到各节段的应力分布,据此选择截面面积相对较小,索力较大的18号索节段(全桥共31对索)作为试验节段.根据圣维南原理,将2.5 m的标准节段分别向上向下延伸一定长度,以减少边界条件对于所选节段受力的影响,通过对3.2 m、3.4 m、3.6 m和3.8 m的试验模型进行有限元分析,最终确定的试验模型高度为3.4 m,此高度范围内有7对单向预应力筋.根据应力等效原则将原桥塔的不规则变截面转换为方形的常截面,截面尺寸为5.9 m×5.9 m.为了实现斜拉索的斜向加载,本试验在模型底部设计了预应力混凝土梯形台座,作为张拉斜拉索的反力梁.试验模型的立面图见图 1,索塔截面预应力布置的具体尺寸见图 2,模型试验现场照片见图 3.
试验模型采用C50混凝土(与原桥一致),预应力采用公称直径15.2 mm的钢绞线,抗拉强度标准值fpk=1 860 MPa,弹性模量Ep=195 GPa,每束16根,预应力孔道采用D104/90 mm的塑料波纹管.
1.2 加载方案
将特制的平行钢丝索短索的一端固定于台座,另一端用最大吨位900 t的千斤顶张拉. 依托工程施工顺序为先建造完成整个索塔,再建主梁,每建一节段主梁,安装相应的斜拉索.因此根据实际结构施工和运营阶段不同的受力状态,试验分为以下3个工况:
工况1:单向预应力单独作用.预应力钢束采用单端张拉,控制张拉力3 124.8 kN,所有预应力钢束全部完成张拉.
工况2:正常使用状态.斜拉索索力与预应力共同作用,Z18设计索力P为7 454.4 kN,B18为6 503.9 kN.加载顺序为0→0.4P→0.6P→0.8P→0.9P→1.0P→0.7P→0.5P→0.
工况3:1.2倍超载状态.斜拉索索力与预应力共同作用,Z18超载索力1.2P为8 945.3 kN,B18为7 804.7 kN.加载顺序为0→0.6P→0.8P→1.0P→1.1P→1.2P→0.7P→0.5P→0.
在正式加载前,进行0.3P的预载,检查各仪表、传感器工作情况,消除各种非线性初始影响.
1.3 测点布置
1)应变测量.为方便描述,斜拉索锚固块所在的塔壁称为“前墙”,布置有预应力的塔壁称为“侧墙”.混凝土内部应变通过在普通钢筋上绑扎钢筋计和埋入式振弦传感器来测量.混凝土表面应变通过粘贴表面式振弦传感器测量.测点沿模型高度方向从上至下分6层布置,编号方式采用:层号+点号+测试元件种类,表面式振弦传感器用E表示,埋入式振弦传感器用M表示,钢筋计用N表示;例如4-1E代表第4层1号位置的测点,其用表面式振弦传感器测量.测点的平面布置点位如图4所示(图中仅标注了点号+测试原件,层号未标出).分层示意见图5.前墙外表面索孔附近的测点编号如图6所示(其中层号8表示不规则层,其测点编号也不再遵循图4所示的规则层编号顺序),括号内的编号为另一面前墙对称位置的测点编号.
2)变形测量和裂缝观测.在模型顶部和中部布置电子百分表,共两层,每层4个,布置平面图见图7.在试验模型的表面,按50 cm×50 cm方格画出方格线,试验过程中用读数显微镜观测每级荷载下有无裂缝产生及裂缝分布、宽度和发展情况.
2 有限元数值模拟
有限元数值模拟的结果可为试验设计提供依据,而试验数据又可反观数值模拟的可靠性,因此有限元数值模拟对试验与分析都具有重要意义[[12-13].本文用ANSYS有限元软件按模型的实际尺寸和加载情况建立三维有限元模型(见图8),进行线弹性计算.模型采用solid45弹性单元模拟混凝土实体;link8单元模拟预应力钢筋,通过初应变施加预应力,考虑预应力损失;shell63单元模拟斜拉索套筒.模型忽略普通钢筋的影响.混凝土和预应力钢筋的材料性质按试验中预留试件的实测各项指标取值.
在台座的底面约束模型的竖向位移(Y方向),并在底面的对称轴位置约束顺桥向(Z方向)和横桥向(X方向)的位移.模型顶面自由.按照试验方案先后进行3种工况的计算.
3 试验与有限元计算结果的对比分析
3.1 单向预应力束单独作用
有限元计算的应力云图见图 9.
图9所示的有限元计算结果表明:在单向预应力作用下,模型侧墙内表面预压应力约为-5.83~-3.72 MPa,塔柱底部受台座影响,压应力稍小.侧墙外表面压应力较小,约为-0.88~ -0.50 MPa.模型前墙内表面应力均表现为拉应力,锚块以上达2.53~ 3.75 MPa,锚块及以下部分为0.94~2.53 MPa.前墙外表面中部存在-1.31~-0.37 MPa的压应力,角部及斜拉索索孔下方为0.5~1.5 MPa的拉应力.
将具有代表性的一部分测点的计算值和实测值列于表 1,二者虽有差异,但整体上较吻合,某些测点(如3-6N,2-10N)偏差百分比较大是因为应力绝对值很小,传感器稍有扰动即引起很大百分比误差,但其绝对误差值是很小的.测点2-13E,5-13E位于前墙内表面拐角部位,实测值表现出异常大的拉应力,经检查该部位出现细裂缝,裂缝宽度很小,约为0.05~0.08 mm,裂缝分布见图 10.文献表明此处细裂缝非本文研究的新型单向预应力体系索塔锚固区所独有,U型预应力体系亦无法避免前墙内侧出现高拉应力区[[1,14],然而张拉大吨位斜拉索力之后,此拉应力将被抵消,在桥梁的使用过程中将不会存在高拉应力区.为避免施工阶段产生局部细裂缝影响混凝土结构的耐久性,建议局部增加防裂钢筋网或局部构造优化,同时控制预应力施工程序.
实测值和计算值均表明,在单向预应力作用下,桥塔侧墙出现了较大的压应力增量,压应力由内表面向外表面逐渐减小,模型内表面中部的传感器测得压应力为-6.0~ -4.0 MPa左右,预应力作用效果明显.前墙内表面的中部出现较大的拉应力,并有细裂缝出现,其他部位未发现裂缝,大部分测点计算值与实测值吻合良好,实测值略小于计算值.
3.2 正常使用状态
有限元计算的应力云图见图11,计算结果表明:在单向预应力和1.0倍工作索力的共同作用下,模型侧墙仍存在-3.5~ -2.5 MPa左右的压应力.张拉预应之后在前墙内表面产生的高拉应力区,施加索力后有所改善.前墙外表面斜拉索套筒附近存在较大拉应力.
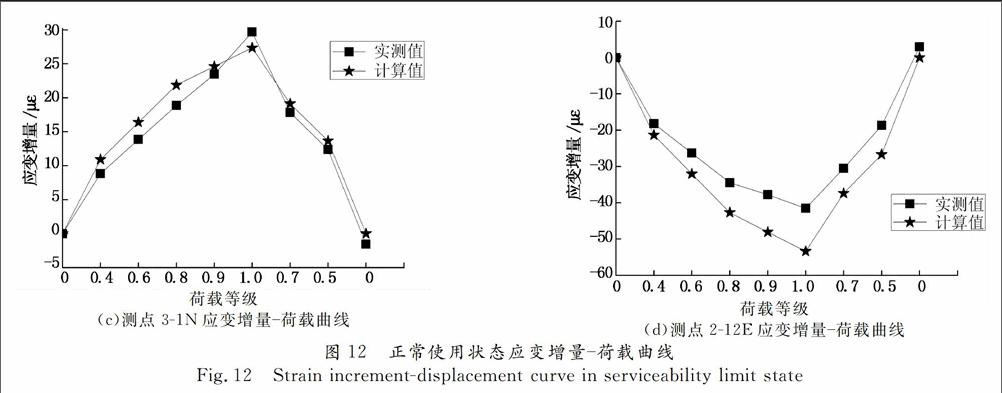
限于篇幅,仅将塔壁具有代表性的部分测点的应变增量荷载曲线绘于图12.
图 12(a)中各测点的荷载应变关系基本呈线性关系,可以看到前墙内表面的测点(2-21E)在设计索力下出现较大的压应变增量,这将抵消预应力施工时出现的拉应力.前墙的关键区域为外表面中部,此位置的测点3-23E出现拉应变增量,在1.0P为55.3 εμ,叠加上一工况应力之后,此区域会出现0.66 MPa的拉应力,小于C50混凝土的容许拉应力2.64 MPa.侧墙的关键区域为内表面的拐角部位,测点2-18E的拉应变增量在1.0P为92.2 εμ,与预压应力叠加之后仍存在-3.26 MPa的压应力.侧墙的拉应变增幅大于前墙,说明侧墙受力较大,单向预应力体系是合理的.
图 12(b)中的测点位于索孔附近,当加载至0.6P时,应变陡然增大,经检查在前墙外表面4个索孔下方均出现细裂缝,但随着荷载的增加裂缝几乎不增长,宽度为0.05 mm左右,加载1.0P时长度为15 cm左右.在文献[14-15]等布置U型预应力混凝土索塔的足尺模型试验中也观测到了类似裂缝,认为此处细裂缝虽较早出现,但应力能够有效地进行重分布,裂缝随荷载增加开展缓慢,不致于过早地危及整体结构的安全,且通过增加防裂钢筋网等构造措施可以有效地避免.有限元分析及文献表明索孔对于前墙应力规律的影响不大,只对索孔附近混凝土应力分布有影响[[16],裂缝不随荷载规律增长说明此处裂缝属于局部应力集中引起的裂缝,随着局部应力重分布具有自限性.
模型其他部位未发现裂缝.
图12 (c),(d)给出了计算值与测试值的对比结果,二者变化趋势吻合较好,计算值普遍稍大于实测值.
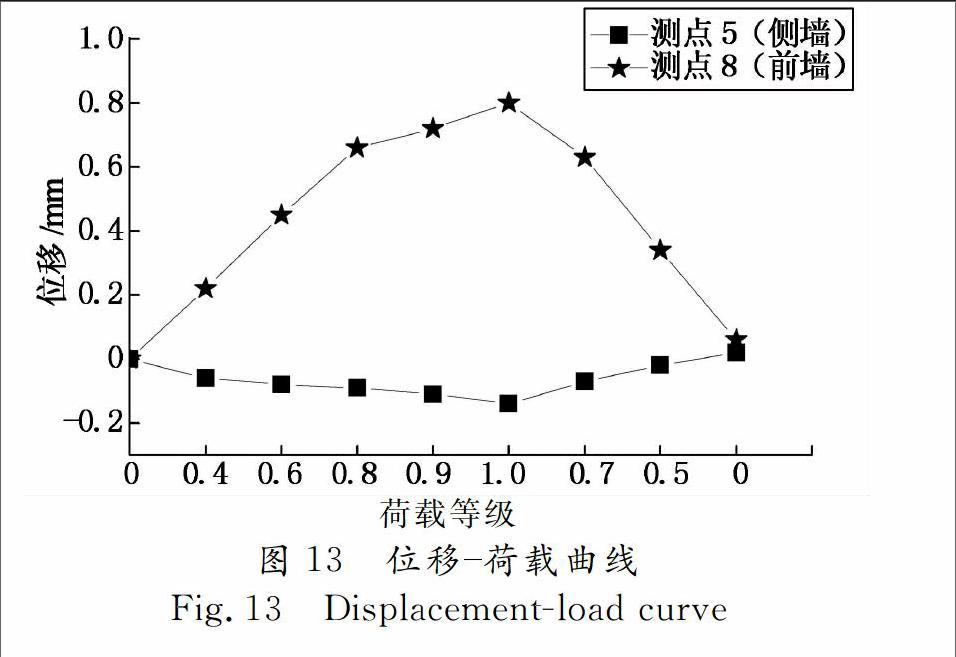
图13给出塔顶2个测点的位移,模型前墙外凸,侧墙内凹,前墙变形大于侧墙.
3.3 倍超载状态
模型试验中一些关键测点的应变增量荷载曲线如图 14所示,大部分测点的变化规律是同上一工况(正常使用状态)相似的,应变与荷载的比例基本不变,说明索塔在超载状态下仍处于弹性工作状态.上一工况中索孔附近出现的裂缝几乎未增长,其他主要受力区域未发现裂缝.
由于索塔模型仍处于弹性工作状态,将该工况实测应力增量与预应力作用下的实测应力叠加,得到超载状态下索塔关键位置的应力状态,列于表2.侧墙仍存在-3~ -2 MPa的预压应力,前墙外表面有拉应力存在,超载状态下结构的主要受力部位是安全的,不会开裂.
3.4 抗裂安全系数的推算
根据有限元及试验结果分析,索塔的危险区域主要为前墙外表面中部以及侧墙内表面拐角处,因此以上述二者为控制区域近似推算索塔的抗裂安全系数,推算数据采用实测值[17].在1.0倍工作索力的作用下,中跨前墙外表面中部测点3-23E测有1.91 MPa的拉应力增量,侧墙内表面拐角处测点2-18E测有3.18 MPa的拉应力增量;而在单向预应力束作用下,前墙测点3-23E处有-1.25 MPa的压应力,侧墙测点2-18E处有-6.44 MPa的压应力.若以2.64 MPa拉应力作为开裂临界值[18],则开裂荷载计算如下:
前墙开裂荷载:pqcr=2.64+1.251.91×1.0p=2.04p.
侧墙开裂荷载:pccr=2.64+6.443.18×1.0p=2.86p.
侧墙与前墙开裂荷载比值:q=pccrpqcr=2.86p2.04p=1.40.
因此,前墙的抗裂安全系数为2.04,侧墙为2.86,整个结构的抗裂安全系数由前墙控制,取为2.04,可见单向预应力束布置使得索塔有足够的安全储备来抵抗斜拉索力,但前墙与侧墙的抗裂安全度不均衡,前墙先于侧墙开裂,建议通过优化分析确定更加合理的预应力位置.
4 结 论
1) 索塔在张拉单向预应力之后,侧墙存在较大的压应力储备,前墙内表面有高拉应力区出现,施加索力可以抵消该区域的拉应力.
2) 在单向预应力和工作索力的共同作用下,侧墙全截面受压,前墙内表面受压,外表面有较小的拉应力出现.1.2倍超载状态下,结构仍处于弹性受力状态.
3) 前墙外表面索孔附近在施加0.6P索力之后出现细裂缝,随着荷载增加裂缝几乎不增长,这是由于局部应力集中引起的,随着局部应力重分布裂缝具有自限性,建议通过加防裂钢筋网等构造措施来改善.
4) 索塔的抗裂安全系数为2.04,单向预应力束布置使其具有足够的安全储备来抵抗斜拉索力;前墙与侧墙的抗裂安全度略有不均衡,前墙先于侧墙开裂,建议通过优化分析确定更加合理的预应力位置.
5) 在弹性受力阶段,实测值和计算值吻合较好,说明建立的有限元模型可以较为准确地反映实际结构,因此,有限元模型可用于索塔的进一步参数分析.
试验和有限元计算表明,单向预应力体系混凝土索塔受力明确合理,并且有效地避免了U型和井型预应力布置施工困难、应力分布不均衡、截面削弱大等缺点,可以在进一步优化后推广其应用.
参考文献
[1] 叶华文,徐勋,李翠娟. 大跨斜拉桥混凝土索塔锚固结构形式比较[J]. 重庆交通大学学报:自然科学版, 2014,33(3): 11-15.
[2] 申卫. 郑州黄河公铁两用大桥索塔锚固区受力特性试验研究[D].长沙:中南大学土木建筑学院, 2010:5-6.
[3] 傅强,张泽鹏,严学寨. 斜拉桥结构优化设计初探[J]. 湖南大学学报:自然科学版,2001,28(3): 109-115.
[4] 王锋君,项贻强. 斜拉桥索塔节段足尺模型试验与分析研究[J]. 桥梁建设,2001,14(2): 8-11.
[5] YU X, JIA B, WANG W, et al. Full-scale model test for anchorage zone of pylon of cable-stayed bridge[C]// Applied Mechanics and Materials. Switzerland:Trans Tech Publications, 2012,238:728-732.
[6] 刘世建. #字型预应力体系在索塔锚固区的应用及试验研究[D].重庆:重庆交通大学土木工程学院, 2008:14-16.
[7] 叶华文,李翠娟. 独斜塔斜拉桥预应力索塔锚固区模型试验研究[J]. 西南交通大学学报,2014,49(1): 52-58.
[8] 洪彧,何锋,勾红叶,等. 曹娥江大桥主桥索塔锚固区节段足尺模型试验方案与空间受力性能研究[J]. 土木工程学报,2013,46(S1): 214-219.
[9] 李跃,朱宏平. 斜拉桥异形截面索塔锚固区足尺模型试验与应力分析[J]. 桥梁建设,2011,22(1): 30-34.
[10]陶齐宇. 大跨度斜拉桥预应力混凝土索塔关键问题研究[D].成都:西南交通大学土木工程学院, 2012:7-8.
[11]叶华文,肖林,李翠娟,等. 大跨斜拉桥预应力索塔锚固区受力机理及试验[J]. 哈尔滨工业大学学报,2013,45(12): 78-85.
[12]刘腾喜,罗松南. 斜拉桥拉索锚区箱梁的空间应力分析[J]. 湖南大学学报:自然科学版,1996, 23(4): 42-45.
[13]戴公连,粟淼,刘文硕,等. 槽型断面梁斜拉桥塔梁墩固结区受力特性研究[J]. 湖南大学学报:自然科学版, 2014,41(1): 27-32.
[14]张晋,杨小敬,张建设,等. 索塔节段足尺试验及其全过程仿真分析[J]. 土木工程学报,2010,43(S2): 158-163.
[15]郭凡,杨永清,周厚斌,等. 斜拉桥索塔锚固区节段足尺模型试验与分析[J]. 建筑结构,2012,42(10): 71-74.
[16]吉林. 润扬长江公路大桥建设:第2册,科研、试验与勘测[M]. 北京: 人民交通出版社, 2005:582-585.
[17]JO B, BYUN Y, TAE G. Structural behavior of cable anchorage zones in prestressed concrete cable-stayed bridge[J]. Canadian Journal of Civil Engineering,2002, 29(1): 171-180.
[18]JTG D62-2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京: 人民交通出版社, 2004: 10-11.
