基于不规则三角网的等值线填充算法
2016-11-08李英娜
杨 玺 吴 晟 李英娜 李 川
(昆明理工大学信息工程与自动化学院 云南 昆明 650500)
基于不规则三角网的等值线填充算法
杨玺吴晟李英娜李川
(昆明理工大学信息工程与自动化学院云南 昆明 650500)
现有基于不规则三角网的等值线填充算法较少,且不能精确判断区域颜色。对此给出一种通过不规则三角网快速填充等值线图的算法,搜索出所有开区域轮廓,通过围成区域等值线属性值与不同颜色的对应关系确定区域颜色,采用深度优先的方法对开区域及其内部的多级封闭区域进行矢量填充。对不同数据源运行该算法,并与其他算法进行比较,根据对比结果可知该算法比现有算法更适合于基于三角网生成的等值线图精确填充。
等值线图颜色填充三角网对应关系深度优先
0 引 言
利用规则矩形网格和不规则三角网TIN(Triangulation Irregular Network)方法可以生成等值线,对等值线围成的区域进行颜色填充能够使等值线图更直观地反映区域的属性值范围。为了使等值线图准确反映数据分布情况,需要找到一种合理的算法生成并填充等值线。
传统的等值线生成与填充通常采用规则网格法,但很多时候需要在一个不规则空间内生成等值线,即离散数据点坐标分布没有规律性。此时,如采用规则矩形网格方式绘制等值线,首先需要采用插值法将不规则离散点集变为规则网格离散点集,但等值线的走向往往与实测有一定偏差。而采用三角网方法生成的等值线能很好地解决这一问题。
郑元满等[1]通过样本点与等值线属性值比较来填色,简化了填色过程,但是采用矩形网格追踪算法生成等值线,偏离原始数据分布情况。张登荣等基于等值线的拓扑关系实现等值线填充[2],通过拓扑树可以矢量填充等值线区域,但是没有给出颜色确定方法。韩丽娜[3]等采用双属性法来进行区域的颜色确定,通过围成区域的等值线平均值确定区域颜色,方法简单,但是颜色与区域属性值有一定偏差。李强等[4]针对温度分布等值线利用围成区域的属性值变化趋势来判断区域颜色,对于由显著趋势的等值线图可以准确填色,但是不能适应复杂趋势情况。刘冬韡等[5]通过等值线分类确定填色顺序,引入格点数据进行颜色确定,填色准确,但是对于含大量闭合区域的等值线图填充过程较慢。
为此,本文给出了一种基于不规则三角网的等值线图填充方法,采用逐点插入法生成TIN的方式绘制等值线,无需对离散数据网格化,更能精确反映离散数据分布情况。并通过两点属性值比较与深度优先搜索的方法确定填充区域颜色,填色准确,效率较高。
1 算法原理与数据结构定义
生成等值线图并填充颜色,主要是在原始离散数据的组成的空间点集上用逐点插入法建立TIN[6],采用线性插值法生成所有等值线[7,8],确定填充区域的轮廓与颜色,再进行矢量填充。
等值线图中的填充区域可以分为开区域和封闭区域两类,其中,开区域由一条或几条等值线与等值线图边界的子线段确立,闭合区域由一条封闭的等值线确立。等值线图可以既含有开区域也含有闭区域,也可以只含有开区域或者只含有闭区域,需要分情况进行填充。
这里定义一条等值线即为单等值线,则未填充颜色的等值线图G拥有n种具有不同Z值(属性值)的等值线,且每种等值线有mi(mi≥ 1)条单等值线。则:
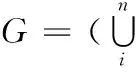
(1)
Contourline_Si={SingleLinej|Z(SingleLinej)=Zi}j≤mi
(2)其中,Contourline_Si为Z值为Zi的等值线集合,BoundaryLines为边界线集合,SingleLinej为Contourlines_Si中的第j条单等值线。
算法采用C++实现,具体数据结构定义如下:
数据结构1单等值线集数据结构
class Contourline_S
{
public:
float Z;
//等值线属性值
list
//Z值相同的等值线集合
};
其中,SINGLELINE为自定义的一个具有属性的单条等值线的数据结构:
数据结构2单等值线数据结构
typedef struct _SINGLELINE
{
list
//具有具体属性值的单条等值线
}SINGLELINE;
其中,Cline为一个线段类。
2 填充算法
对于等值线图的填充,关键是要确定开区域或封闭区域的颜色,这需要建立一张颜色表,通过等值线属性值与颜色的对应关系来确定填充区域颜色。
2.1颜色表的建立
具有n+1种颜色的等值线图应包含n种具有不同Z值的单等值线集。据此,可以为等值线图建立一个具有n+1个颜色值的并且按所表示Z值大小升序排列的颜色表ColorTable(即一个颜色数组Color[n+1])。ColorTable与按属性值升序排列分类的单等值线集数组Contourline[n]的构成及对应关系如图1所示。
具体颜色值Color[i]、Color[i+1]与属性值为Zi的单等值线集合Contourline[i]具有对应关系,可以表述为:在属性值为Zi的单条等值线两侧的区域颜色为Color[i]和Color[i+1]。通过这种关系,便可以确定由等值线围成区域的颜色。
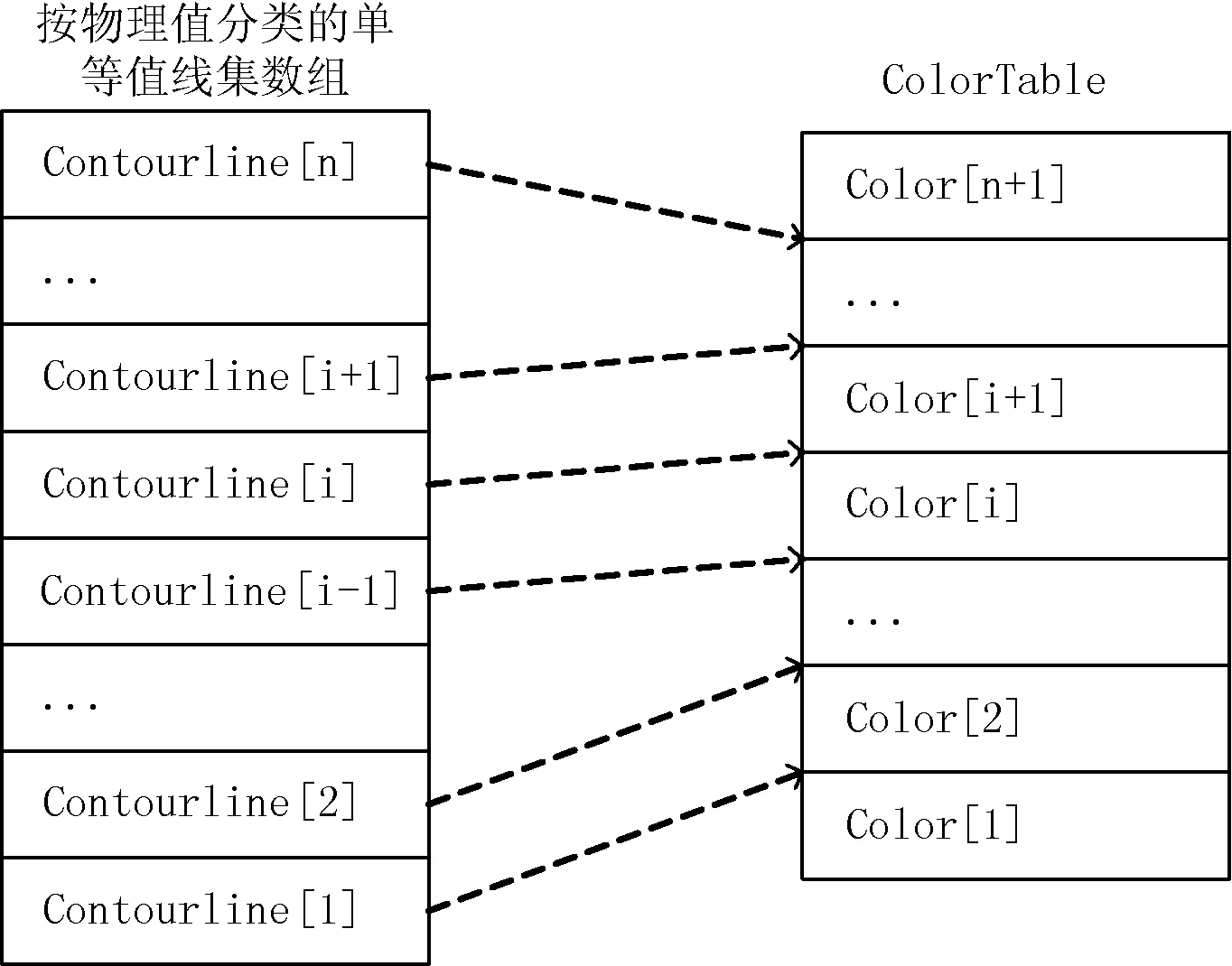
图1 单等值线集与颜色对应关系
2.2含有开区域的等值线图填充
首先,利用线性插值法可以绘制出所有等值线。基于TIN中三角形边采用线性插值法生成等值线的公式为:
(3)
(4)
其中,(x1,y1)、(x2,y2)分别为三角网一边两个端点的坐标,z1、z2为该边两个端点的属性值,x、y为在该边上插入等值点的坐标,z为该等值点的属性值。生成的单等值线集数组为Contourlines[n]。
然后,找到TIN的边界点集,把所有单等值线端点插入到该点集中,对新点集逆时针排序,利用边界点追踪算法生成一个新的开区域轮廓[9],采用深度优先策略对开区域及其内部的封闭区域进行颜色的确定与填充。
对所有开区域及其内部的封闭区域都按上述方法进行操作,便完成了整个等值线图的填充。流程如图2所示。
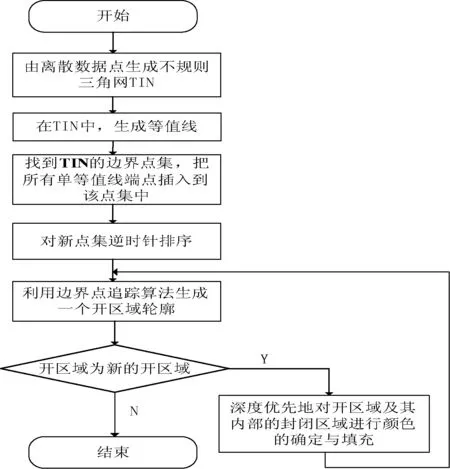
图2 含有开区域等值线图的填充流程
2.2.1边界点集合的生成
对TIN内的每个三角形存储三个边的邻接三角形信息。如果一个三角形的某条边没有邻接三角形,则该条边即为TIN的边界子线段。此时,TIN的边界由在原始数据点集中并且在边界子线段上的点连接而成,设该点集为ST。
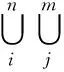
S={Pi|Pi∈ST}∪{LPi|LPi∈SL}
(5)
如图3所示,将该点集按空间关系逆时针排序,并存储在有序边界点列表S′中。
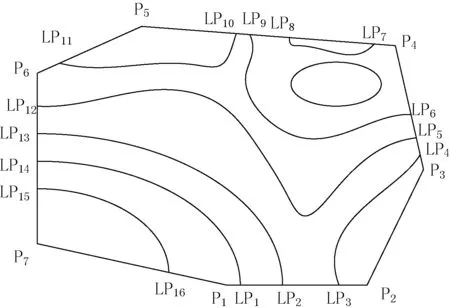
图3 边界点集分布
2.2.2开区域的填充1) 确定开区域轮廓
利用边界点追踪填充区域的方法,确立一个由非闭合等值线和边界线段组成的开区域Ri。并设该区域轮廓点集中的第一个在S′中并且是单等值线端点的点为A。然后,找到S′中排在点A前面的一个点,设为A′(若A为S′中第一个点,则A′为S′中的最后一个点)。
2) 确定开区域颜色并填充
开区域包括两种模式:
模式1由Z值为zi的等值线组中的一条单等值线和边界中的线段围成(如图4中单等值线L1和边界线段Lc1、Lc2围成的区域R1);
模式2由Z值为zi和zi±1的两个等值线组中的一条或多条单等值线和边界线段围成(如图4中单等值线L1、L2、L3和边界线段Lc3、Lc4、Lc5围成的区域R2)。
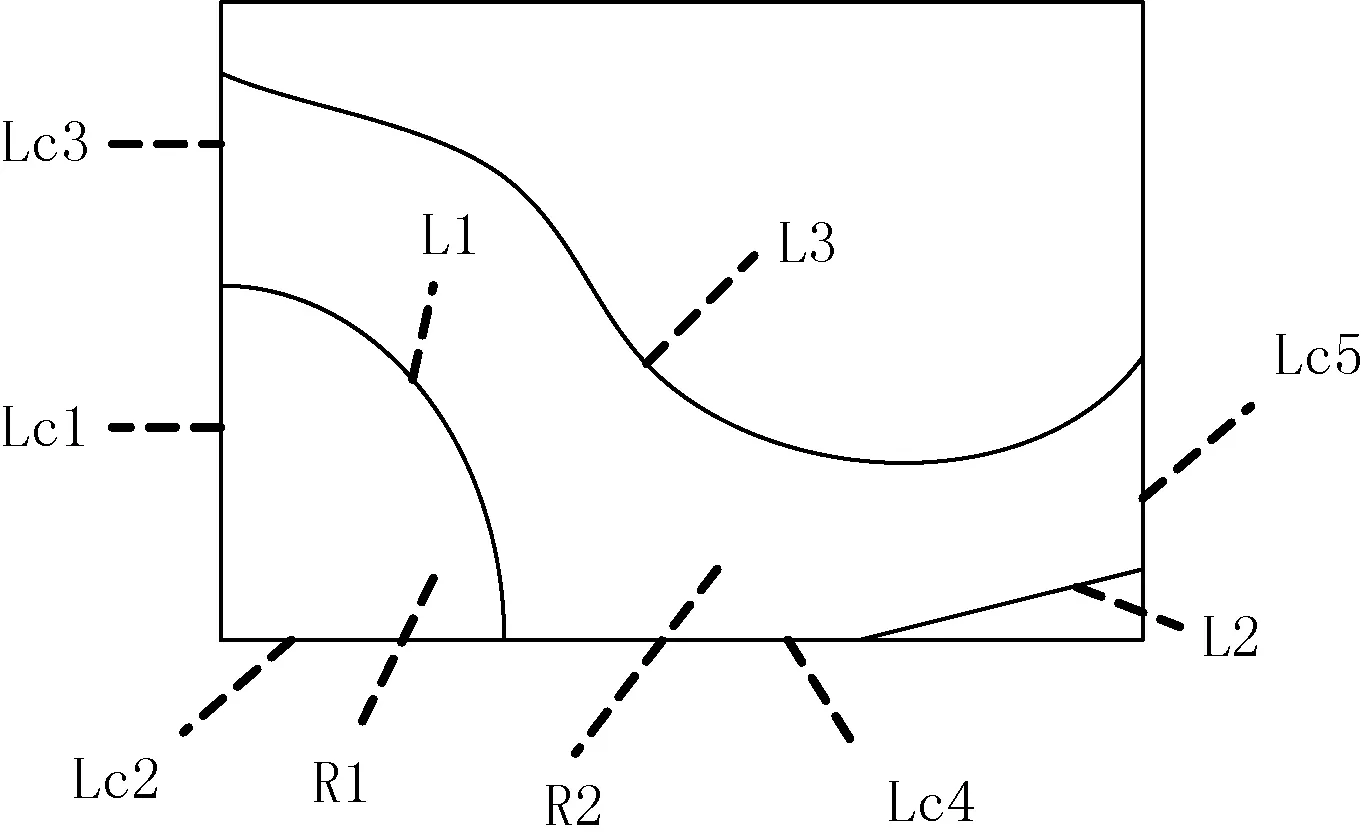
图4 开区域分类
文献[10]通过围成开区域等值线属性值个数与大小确定颜色,需要知道区域轮廓所有等值线的属性值,计算量大,为此,本文通过两点比较法来确定开区域颜色。 方法如下:
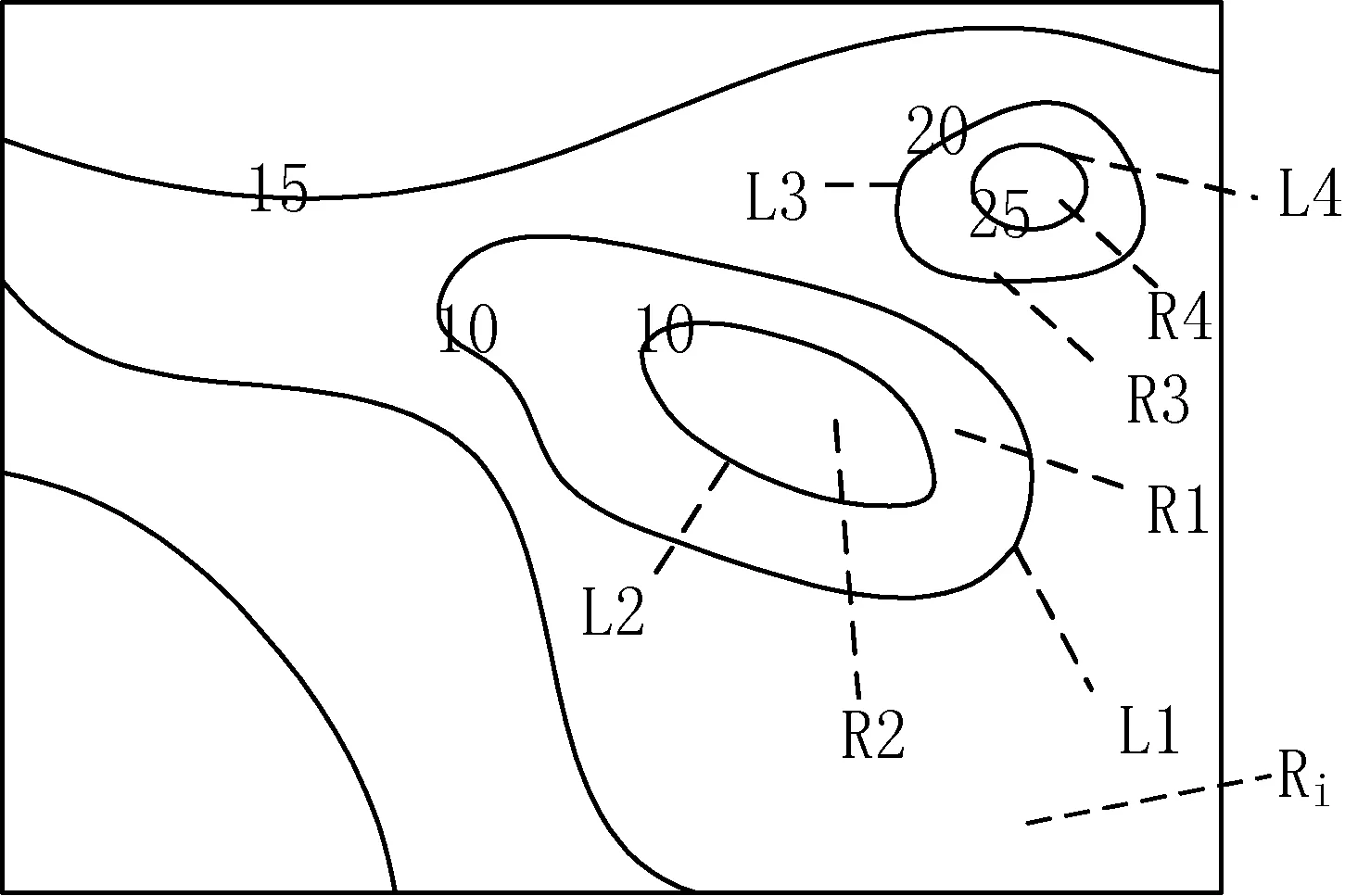
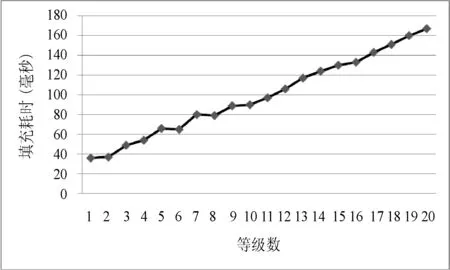
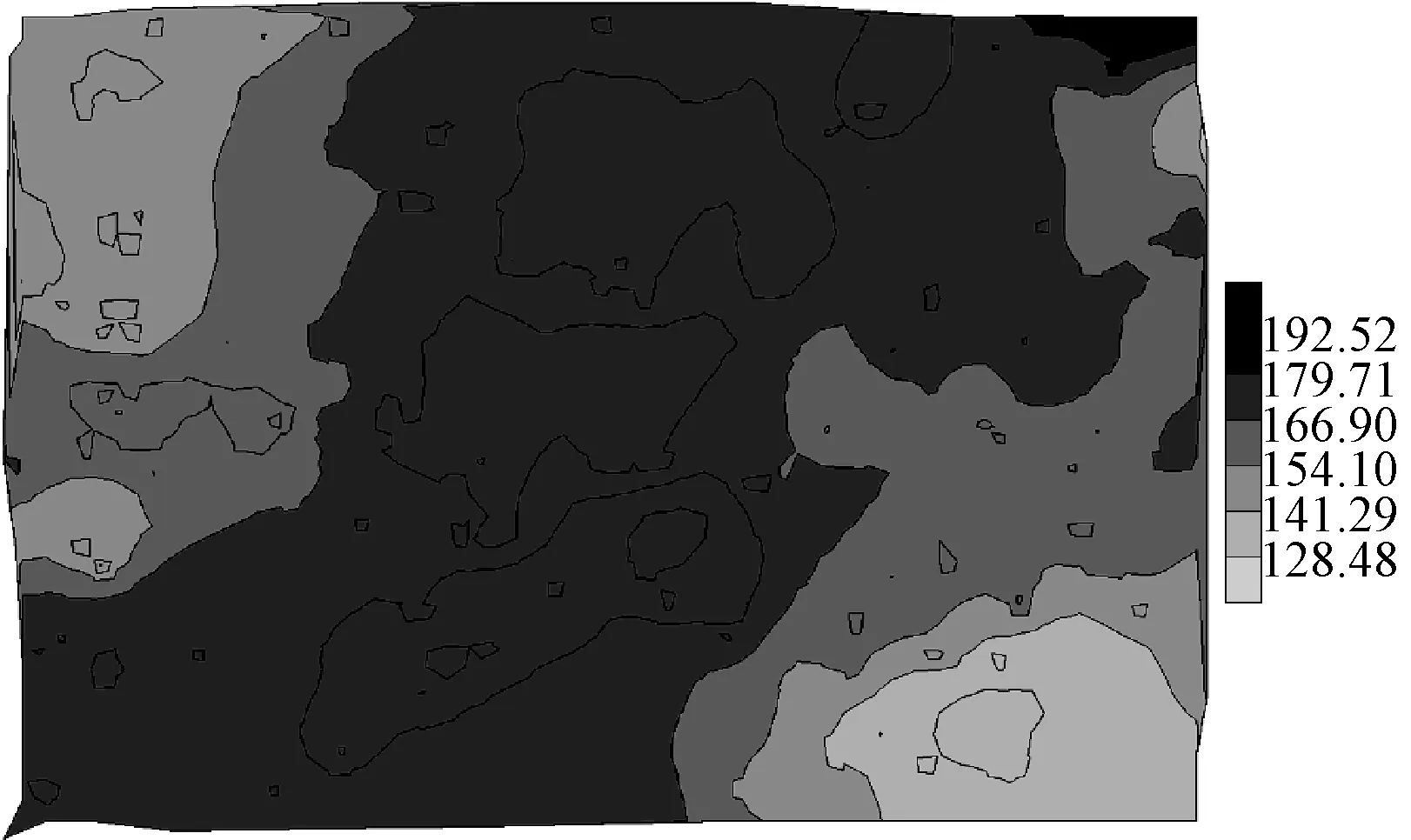
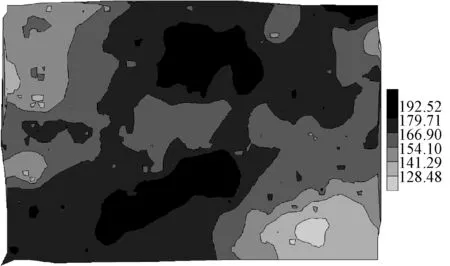
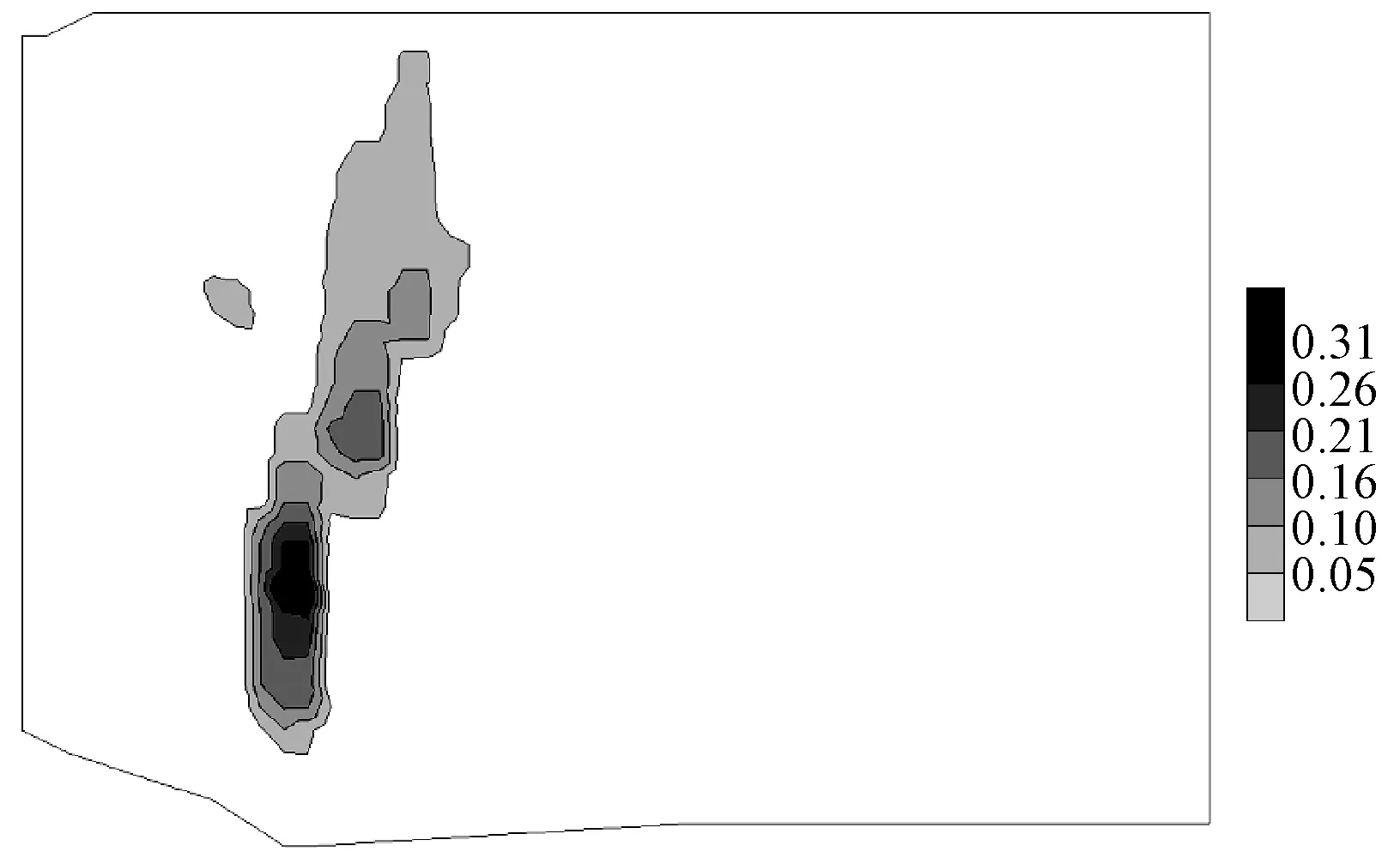
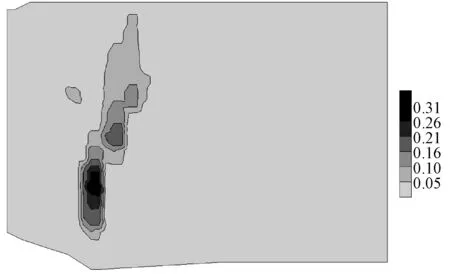
(1) 如图5(a)所示的区域Ri,A′∈ST,即点A′不是等值线端点,而是三角网点。此时,由于A′在填充区域Ri的内部,如果设点A所在单等值线的索引比较Z(A′)与Z(A)的大小,如果Z(A′)>Z(A),则Color(Ri) =Color[i+1],如果Z(A′) 算法1 if(ContourlineIndex(Z(A)) == i) if Z(A′)>Z(A) set Color(Ri) = Color[i+1]; else if Z(A′) set Color(Ri) = Color[i]; Fill(Ri,Color(Ri)); 其中,ContourlineIndex(Z(A))为A点所在单等值线集在Contourline[n]中的索引,Fill(Ri,Color(Ri))为填充区域函数。 (2) 如图5(a)中的Ri′所示单等值线与边界线段围成开区域情况。由式(3)、式(4)可知,单等值线两头必然落在两条不同的三角网边上,所以Ri′轮廓中,必然有一个以上的集合ST中的点。所以单等值线围成区域的颜色值可以由算法1确定。 (3) 如图5(b)所示,A′∈SL,即点A′为单等值线端点。此时,A′为单等值线上的点,但是,如果在线段AA′上取一个虚拟的点A″,则A″的Z值有两种情况:一是Z(A″)>Z(A),二是Z(A″) 图5 开区域颜色确定方法 上述方法(1)-方法(3)中,Z(A)>Z(A′)或Z(A) 如果如图5(a)所示,A′∈ST(即A′为原始数据点)或者如图5(b)所示,A′∈SL(即A′为等值线上的点),则A、A′必然在TIN中同一个三角形的同一条边上(如果A、A′在TIN中三角形的两条不同的边上,则A、A′之间必定有一个三角形边的顶点属于集合ST)。此时,由于采用的等值线生成算法为线性插值法,则该边上的任意两点属性值必然不等,即点A、A′的属性值必然不相等。 这样即使不知道围成开区域所有等值线的属性值也能确定开区域颜色。 2.2.3封闭区域的填充 对于封闭区域的填充,无论是文献[3]提出的双属性算法还是文献[4]提出的趋势判断法,都无法对内部不包含子封闭区域的封闭区域的颜色进行准确判断。为此,本文给出一种利用已填充区域颜色值,逐级进行深度遍历填充子封闭区域的方法。 如图6所示,L1或L3围成的封闭区域R1、R3被区域Ri所包围,如果两个区域之间只隔着一条单等值线即为相邻区域,则区域R1、R3与Ri是相邻的,并R1、R3为Ri的一级子封闭区域。同样的,R2与Ri不相邻,与R1相邻,为R1的一级子封闭区域,且说R2为Ri的二级子封闭区域,R4与R2类似。一个开或闭区域的多级子封闭区域的定义以此类推。由于含有开区域的等值线图中的封闭区域一定是由某一个开区域包含的,所以只要对所有开区域的一到多级子封闭区域逐级填充便可以完成整个等值线图的填充。下面结合图6给出的具有代表性的示例,对一个开区域及其内部所有子封闭区域逐级填充的具体方法。 设图6中的开区域Ri为当前已填充区域R,并设Color(Ri)的颜色表索引为i,即Color(Ri)==Color[i]。由图1所示单等值线与颜色的对应关系可知,R的一级子封闭区域颜色为Color[i+1] 或者Color[i-1]。如果一级子封闭区域的颜色为Color[i+1],则其轮廓为单等值线集Contourline[i].SingleLines[mi]中的一条单等值线,如果颜色为Color[i-1],则其轮廓为Contourline[i-1].SingleLines[mi-1]中的一条单等值线。找到单等值线集Contourline[i].SingleLines[mi]和Contourline[i-1].SingleLines[mi-1]中被Ri的轮廓包含且围成区域与R相邻的封闭单等值线即为R的一个一级子封闭区域轮廓。 判断Contourline[i].SingleLines[mi]或者Contourline[i-1].SingleLines[mi-1]中的一条单等值线Lt围成区域Rt与R相邻与否的具体方法为:如果Lt(图6中的L1、L3)不被其他同属性值的封闭单等值线包含,则Rt为R的一级子封闭区域(图6中的R1、R3)轮廓,对Lt围成的区域Rt进行填充;如果Lt(如图6中的L2)被其他同属性值的一条封闭单等值线(图6中的L1)包含,而且包含Lt的这条同属性值单等值线围成的区域(设为图6中的R1)没有被填充,则代表Lt围成区域Rt与R不相邻,暂不对其进行填充。 在对图6中Ri的二级子封闭区域R2、R4填充时,可以递归地将当前区域R由Ri换为R1及R3,再对R的一级子封闭区域进行填充操作即可,同样地,Ri的多级子封闭区域也采用类似方法进行填充,直到当前区域R没有相邻子封闭区为止。 图6 封闭区域分布情况 2.3不含开区域的等值线图填充 有时等值线图中只包含封闭区域,如图7所示。这种情况下,由于等值线图边界上没有等值点,需要把边界当做一个特殊的开区域RS进行填充。由于边界中必然包含一个三角网点PS,由图1可知,只需比较PS的属性值Z(PS)与单等值线集数组Contourline[n]中的Contourline[i]属性值Z(Contourline[i])大小即可确定RS的颜色。例如,如果Z(PS) >Z(Contourline[i])且Z(PS) 图7 不含开区域的等值线图示例 2.4复杂度分析 本文算法对开区域的填充采用两点属性值比较方法,在等值线图由t个开区域,且每个开区域由k条非封闭等值线围成的情况下,仅需进行属性值的t次比较就能确定开区域颜色,时间复杂度为O(t)。对于封闭区域的填充,算法采用深度优先搜索方式确定区域颜色与填充,填充一个封闭区域需对其在属性值上相邻的单等值线集进行遍历。如果等值线图含有n种属性等级,每种等级有m条封闭等值线,算法对封闭区域填充的时间复杂度应为O(nm2)。算法的总时间复杂度为O(t) +O(nm2)。但经过大量数据分析发现,当n线性增长时,t也呈线性增长且速率与n一致,但k、m往往保持在常量水平,故算法的实际时间复杂度为O(n)+O(n)即O(n)。 文献[10]对开区域的填充须记录所有等值线属性值,时间复杂度为O(kt),对封闭区域的填充通过三角网中线段与等值线的空间关系及属性值比较来确定区域颜色,时间复杂度为O(nm),总时间复杂度为O(kt)+O(nm),由上述分析可知,实际时间复杂度应为O(n)+O(n)亦即O(n)。但三角网生长方法效率较低[6],已经很少有人使用,本文算法采用逐点插入法生成三角网,故本文算法在实用性上更高。 采用C++与OpenCV编程实现上述算法。图8为通过对一组数据20种不同属性等级的等值线图进行本文算法实现的耗时曲线,从中可以看出算法时间复杂度为O(n)这与2.4节分析的一致。 图8 算法耗时曲线 图9为采用边界扫描算法填充的包含开区域等值线图,该算法不能对闭区域进行填充。图10为利用本文给出方法对包含开区域等值线图的填充结果。可以看出,本文方法准确地填充了封闭区域。 图11为采用文献[10]提出的基于逆生长三角网算法填充的不含开区域等值线图,可见不能对等值线图的边界围成的区域进行填充。图12为采用本文方法填充的不含开区域的等值线图。通过对比可以看出,本文方法对于包含或者不包含开区域的等值线图均能进行较好的填充。 图9 含开区域等值线图的边界扫描算法填充结果 图10 含开区域等值线图的基于本文算法填充结果 图11 不含开区域等值线图的基于逆生长三角网算法填充结果 图12 不含开区域等值线图的基于本文算法填充结果 本文先采用逐点插入法生成TIN,再生成等值线,充分发挥了TIN方式生成等值线更忠实于原始离散数据分布情况的特点,确保了等值线图的精确性。同时,采用两点属性值比较法判断开区域颜色,采用深度优先遍历方式,根据当前等值线的属性值逐层对包含的封闭区域进行颜色判断。对于一些颜色走势不显著与走势复杂的情况也能够进行很好的填充,且能够对不含开区域的等值线图进行填充。本文实现了对基于TIN生成的等值线图的精确绘制。 通过程序实现,证明了该方法简单、可靠,为等值线图的填充算法研究提供了一个有效参考,且能在地理信息系统开发中得以较好应用。此外,本方法应用在了瞬变电磁探测数据的成图与识别系统中。 [1] 郑元满,姚长利,张晨,等.基于等值线拓扑走向的快速区域填充算法[J].石油地球物理勘探,2010,45(6):899-908. [2] 张登荣,刘绍华,毛天露,等.等值线自动建立拓扑关系算法与快速填充应用[J].中国图象图形学报,2001,6(3):264-269. [3] 韩丽娜,石昊苏,张群会.基于边界点追踪的等值线图区域填充算法[J].计算机工程与科学, 2006,28(11):66-67. [4] 李强,李超,甘建红.基于三角网的等值线填充算法研究[J].计算机工程与应用,2013,49(5):185-189. [5] 刘冬韡,戴建华,林红,等.基于等值线分类的区域填充算法[J].气象科技, 2009,37(5):597-600. [6] 余杰,吕品,郑昌文.Delaunay三角网构建方法比较研究[J].中国图象图形学报,2010,15(8):1158-1167. [7] 付晓东,赵俊三,马绍雄.不规则区域内基于D_TIN的等值线生成算法[J].昆明理工大学学报:理工版,2006,31(6):46-50. [8] 陈宏文,曾繁彩,王刚龙,等.改进Delaunay 三角网格等值线提取方法[J].热带海洋学报,2013,32(4):92-96. [9] 康建荣.不规则区域等值线拓扑关系的建立及充填算法[J].测绘通报,2004(9):7-9. [10] 张道军,李瑞雪,席振铢,等.基于逆生长三角网的等值线图自动填充算法[J].地球物理学进展,2014,29(3):1458-1462. THE CONTOUR FILLING ALGORITHM BASED ON TRIANGULATED IRREGULAR NETWORK Yang XiWu ShengLi YingnaLi Chuan (FacultyofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650500,Yunnan,China) Currently, there are little contour filling algorithm based on triangulated irregular network, and have trouble in judging color regions accurately. In this case, an algorithm of filling contour map rapidly by triangulated irregular network is proposed to search for outlines of all open regions. Then the region color is confirmed by the corresponding relationship between the attribute value of isograms and different colors, and the multistage closed region of open regions and its inside is filled with vectors by using the method of deep optimization. After running the algorithm on different data sources and comparing with other algorithms, it is learned that the proposed algorithm is more suitable to fill contour map generated by triangulated network accurately than other existing algorithms. Contour mapColor fillingTriangulation networkCorresponding relationsDepth-first 2015-07-04。云南省应用基础研究计划项目(2013FZ 021)。杨玺,硕士生,主研领域:地理信息系统。吴晟,教授。李英娜,副教授。李川,教授。 TP391 A 10.3969/j.issn.1000-386x.2016.10.059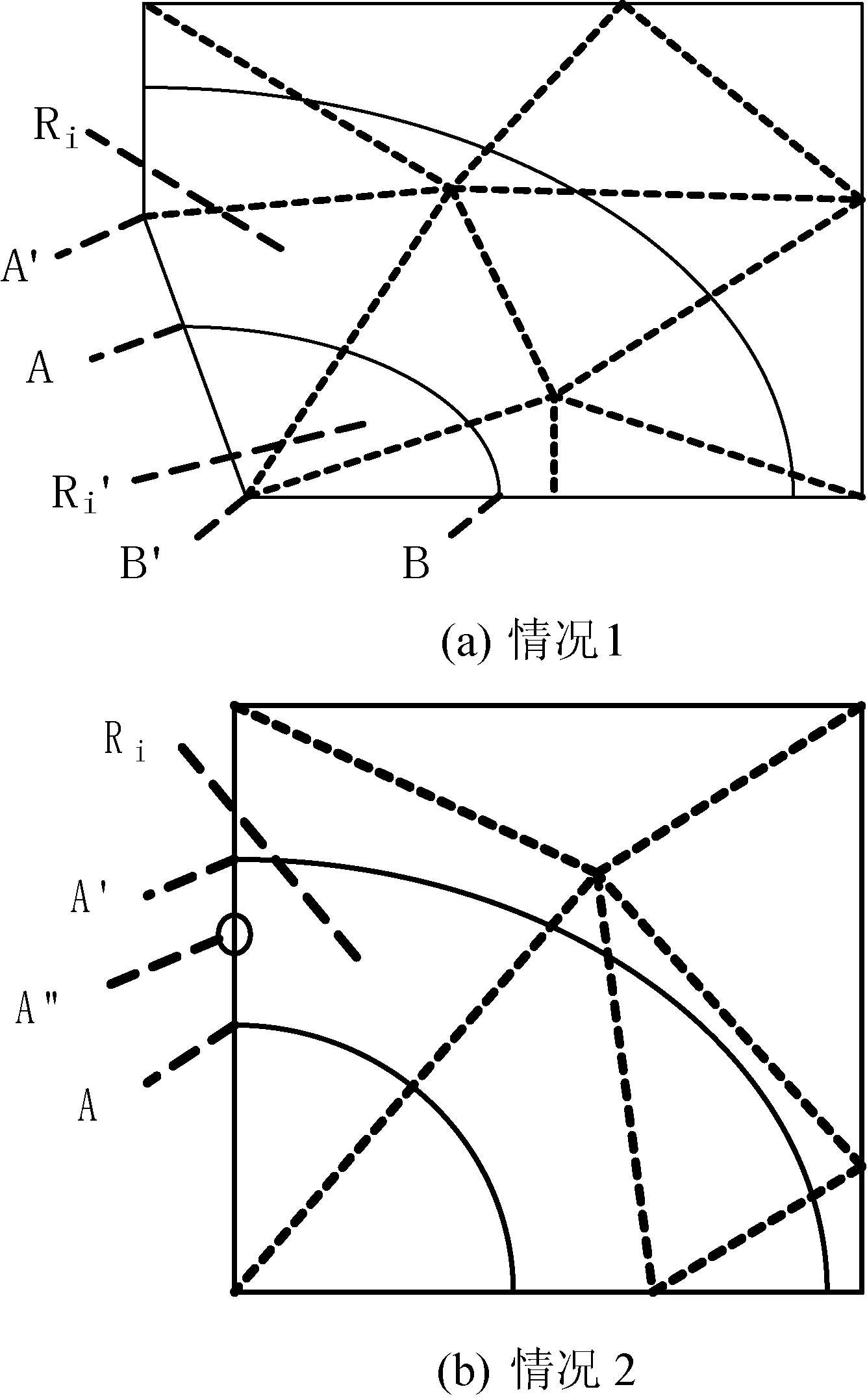
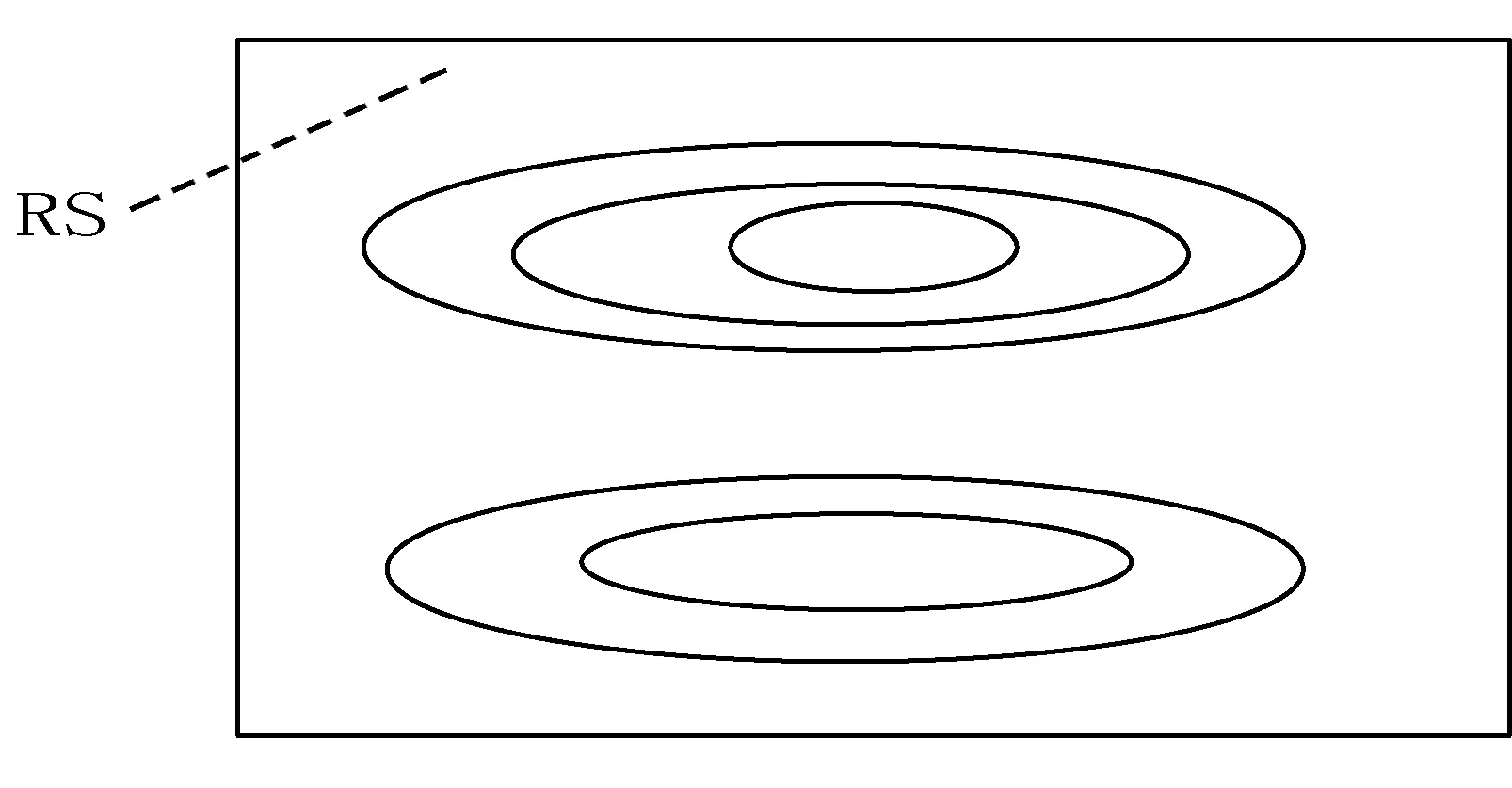
3 实 验
4 结 语
