一种基于极限学习机的缺失数据填充方法

杨　毅　卢诚波

(丽水学院工程与设计学院　浙江 丽水 323000)



一种基于极限学习机的缺失数据填充方法

杨毅卢诚波

(丽水学院工程与设计学院浙江 丽水 323000)

数据处理过程中经常会遇到不完备数据需要填充的问题，寻求简单有效的缺失数据填充方法非常重要。针对该情况，提出一种基于极限学习机ELM(Extreme Learning Machine)的缺失数据填充方法，通过极限学习机网络建模，建立需要填充的缺失属性与其他属性的非线性映射模型。实验结果表明：该方法具有非常好的填充效果。

极限学习机缺失数据填充UCI机器学习数据库

0　引　言

在信息处理过程中，经常会遇到数据集不完整的情况，通常称之为缺失数据。数据缺失产生原因很多，如人为疏忽被遗漏、信息属性值不存在和客观条件难以采集等，数据缺失普遍发生在各个研究领域。处理缺失数据最常用的方法是丢弃数据中不完整的点，只采用数据中完整的点，用减少样本量换取信息的完备，但这样会浪费大量的采集资料，遗漏了隐藏在丢弃数据中的信息。特别是当样本容量较小时，丢弃数据会严重影响到数据的客观性和多样性。因此对缺失数据进行填充是一项非常重要的工作。

对缺失数据进行填充的传统方法有零填充、均值填充、热卡填充、回归填充和多重填充等[1-3]。零填充指的是将缺失值用零替代，但只有当缺失值近似为零时，零填充才能有较好的效果。均值填充指的是将缺失值用已知数据的平均值替换，这种方法也会产生有偏估计。热卡填充指的是在数据集中找到一个与它最相似的值，将缺失值用这个近似值替代，该方法比较耗费时间。K近邻填充是热卡填充的一种方法，它是找到数据集中与缺失数据的欧氏距离最小的K个点，用这K个点的平均值替换缺失值。回归填充指的是将缺失值用缺失数据的条件期望替代。多重填充是用一组近似值替换每个缺失值，再用标准的统计分析过程对多次替换后产生的若干数据进行分析、比较，得到缺失值的估计值。

极限学习机ELM是一种单隐层前馈神经网络(SLFN)学习算法，网络的输入权为随机给定，输出权则通过最小二乘法计算得到。整个训练过程一次完成，不需要迭代过程。与已知的BP算法和支持向量机等算法相比，具有执行过程简单、运行速度快且泛化性能好等特点。该算法已被广泛地应用到模式分类、回归问题[7]、图像识别[8,9]、高维数据的降维算法[10]等各个领域，均取得了非常好的效果。本文基于极限学习机提出一种新的缺失数据填充方法。

1　基于极限学习机的缺失数据填充方法

2004年，黄广斌等提出极限学习机算法[4-6]，该算法只需要设置单隐层前馈神经网络的隐层节点个数，在算法执行过程中不需要调整网络的输入权和隐元的偏置，并产生唯一的最优解。

给定样本容量为N的样本(xi,yi)，其中i≤N，xi∈Rn且yi∈Rm，xi是输入的样本值，yi是输出的期望值。隐层节点数为L的单隐层前馈神经网络可表示如下：

(1)

其中βi=(βi1,βi2,…,βim)T是输出外权，f(x)是激活函数，ωi和xj的内积，oj是输出的真实值，如图1所示。式(1)可表达成矩阵的形式如下：

Hβ=O

(2)

其中 O=(o1,o2,…,oN)T。

(3)

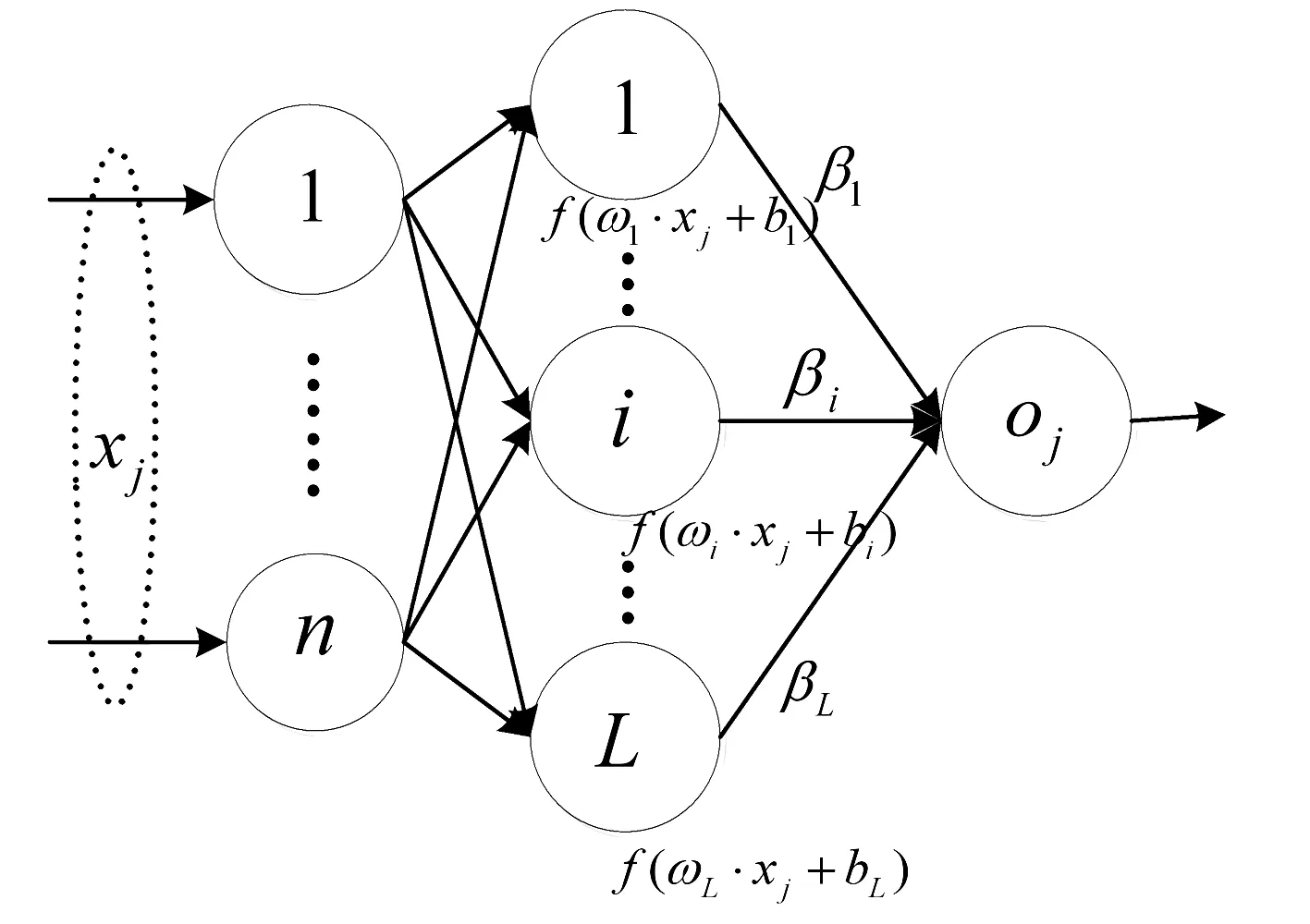
图1　输入权和隐层偏置随机给定的单隐层前馈神经网络

令O=y，其中y=(y1,y2,…,yN)T，则式(2)可表达成：

Hβ=y

(4)

极限学习机算法的基本思想是：随机选取ωi和bi，然后利用β=H†y计算输出外权，其中H†表示H的广义逆。利用正交投影法求H的广义逆可得：

H†=(HTH)-1HT

为了权衡经验风险和结构风险，进一步提高网络的泛化性能，文献[11-14]研究了正则极限学习机,其数学模型为：

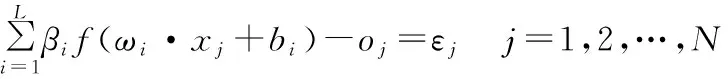
(5)

式中，误差‖ε‖2代表经验风险，‖β‖2代表结构风险，它来自于统计学中边缘距离最大化原理；而γ是两种风险的比例参数，用来权衡这两种风险。

求解上述模型，可得:

(6)

本文设计的基于极限学习机进行缺失数据填充的主要思想是：利用样本集中完备的样本进行极限学习机网络建模，建立需要填充的缺失属性与其他属性的非线性映射模型。例如，若需填充样本的缺失属性为第1个属性，则将第2个属性至第n个属性的值构造成输入向量，将第1个属性的值作为输出向量，利用数据集中的完备样本训练网络的外权矩阵β。最后，将缺失样本的数据代入网络，获得属性1的估计值。

该算法的具体步骤如下：

第1步根据完备样本的数目确定合适的隐层节点个数；

第2步利用完备样本，将缺失属性值作为输出值，其他属性的值作为输入值，通过极限学习机建立缺失样本中的缺失属性与其他属性的非线性映射模型，计算式(6)中的β；

第3步利用缺失样本的剩余属性值计算H, 最后利用式(4)计算缺失属性值。

2　仿真实验

实验将本文的填充方法与零填充、均值填充、K近邻填充方法在广义平均绝对误差和聚类纯度两个指标上进行比较。

广义平均绝对误差(GMAD)可表达如下：

(7)

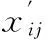
聚类纯度(Purity)[15]表示如下：

其中S={s1,s2,…,sk}表示数据集真实的聚类，s1表示落入s1中的样本数据，C={c1,c2,…,ck}表示人为给予的分类，c1表示落入c1中的样本数据，N为样本数据的数量。显然，聚类纯度越大意味着填充后的数据有效性越高。

本文所用的数据集来自UCI机器学习数据库的鸢尾属植物数据集、乳腺癌数据集、种子数据集、精液活力数据集和僧侣问题数据集。

(1) 鸢尾属植物数据集由Fisher于1936年提供，数据集包含3个类别的鸢尾属植物，每个类别有50个数据。其中，第一类与第二、三两类是线性可分的，而第二类与第三类是非线性可分的。

(2) 种子数据集由波兰科学院的农业研究所提供，该数据集包含3类小麦内核几何结构的测量值。实验者用X射线技术扫描种子内核，把成像图记录在13×18厘米的X射线柯达板上，并获取相关数据。

(3) 乳腺癌数据集是由Ljublijana大学医学中心肿瘤研究所的Matjaz Zwitter和Milan Soklic提供。数据集包含2类：良性肿瘤和恶性肿瘤，每类分别为201个数据和85个数据。

(4) 精液活力数据集是根据WHO 2010标准对100个志愿者的精液分析得到的数据，精液样本被分为正常与不正常两类。该数据集由Alicante大学计算机系的David Gil和生物系的Jose Luis Girela提供。

(5) 僧侣问题数据集由Carnegie Mellon 大学计算机学院的Sebastian Thrun提供给UCI机器学习数据库，通常被用于测试归纳算法。

实验中采用5-折交叉验证[16]，数据集平均分成5份，其中4份作为训练数据集，另外1份作为测试数据集，轮流让其中的1份作为测试样本，其余4份作为训练样本，实验结果取平均值。

实验中依次将测试样本中的前若干个属性作为缺失属性；然后由完备样本(即训练样本)，利用极限学习机算法建立缺失属性与其他属性之间的非线性映射关系；最后利用这个映射关系对测试样本进行填充。通过比较填充数据与真实数据的广义平均绝对误差和聚类纯度两个指标来评价填充数据的效果。

使用的仿真软件为Matlab R2013a，聚类算法采用Matlab 模式识别工具箱中的kmeans函数。该实验环境为：Windows XP操作系统，AMD Athlon(tm)II X2 250 Processor 3.01 GHz，2 GB内存。

表1给出了四种填充方法在5个数据集上的广义平均绝对误差比较和实验数据的细节。由表1可见，对于鸢尾属植物数据集和种子数据集，在四种填充算法中，极限学习机填充方法得到的广义的平均绝对误差最小；对于乳腺癌数据集、精液活力数据集和僧侣问题数据集，极限学习机填充方法在多数情况下得到的广义的平均绝对误差最小，这意味着利用极限学习机填充方法得到的填充数据更接近真实值。

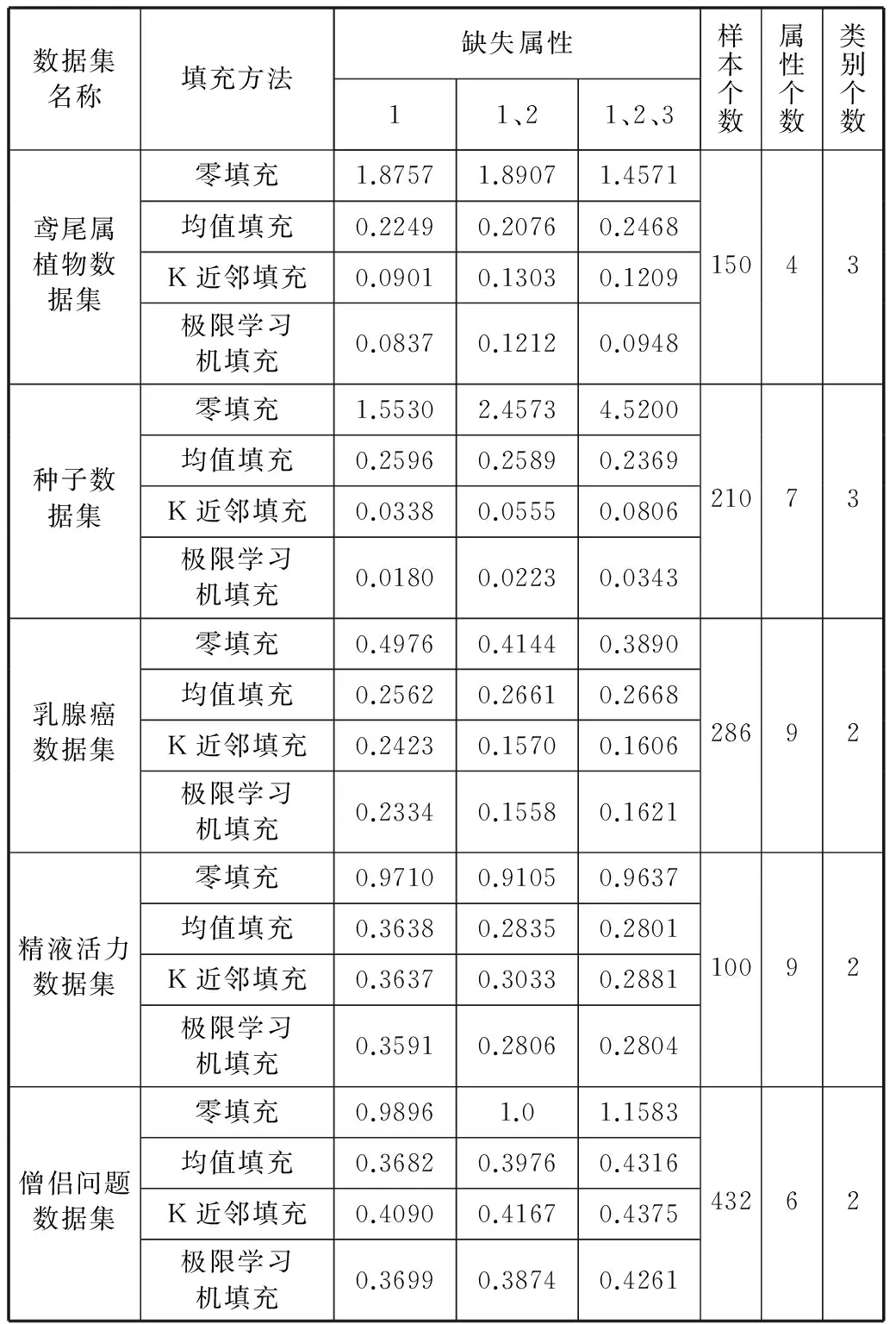
表1　四种填充方法在5个数据集上的广义平均绝对误差比较和实验数据的细节

图2-图6给出了四种填充方法在5个UCI数据集上的聚类纯度比较。可以看出，对于鸢尾属植物数据集、种子数据集和乳腺癌数据集，在四种填充算法中，极限学习机填充方法得到的聚类纯度最高；对于精液活力数据集，四种方法取得的聚类纯度几乎相同；对于僧侣问题数据集，极限学习机填充方法在多数情况下得到的聚类纯度最高，这意味着利用极限学习机填充方法得到的填充数据更具有使用价值。综上所述，本文提出的极限学习机填充方法在多数情况下能取得比其他三种经典的填充方法更好的填充效果。

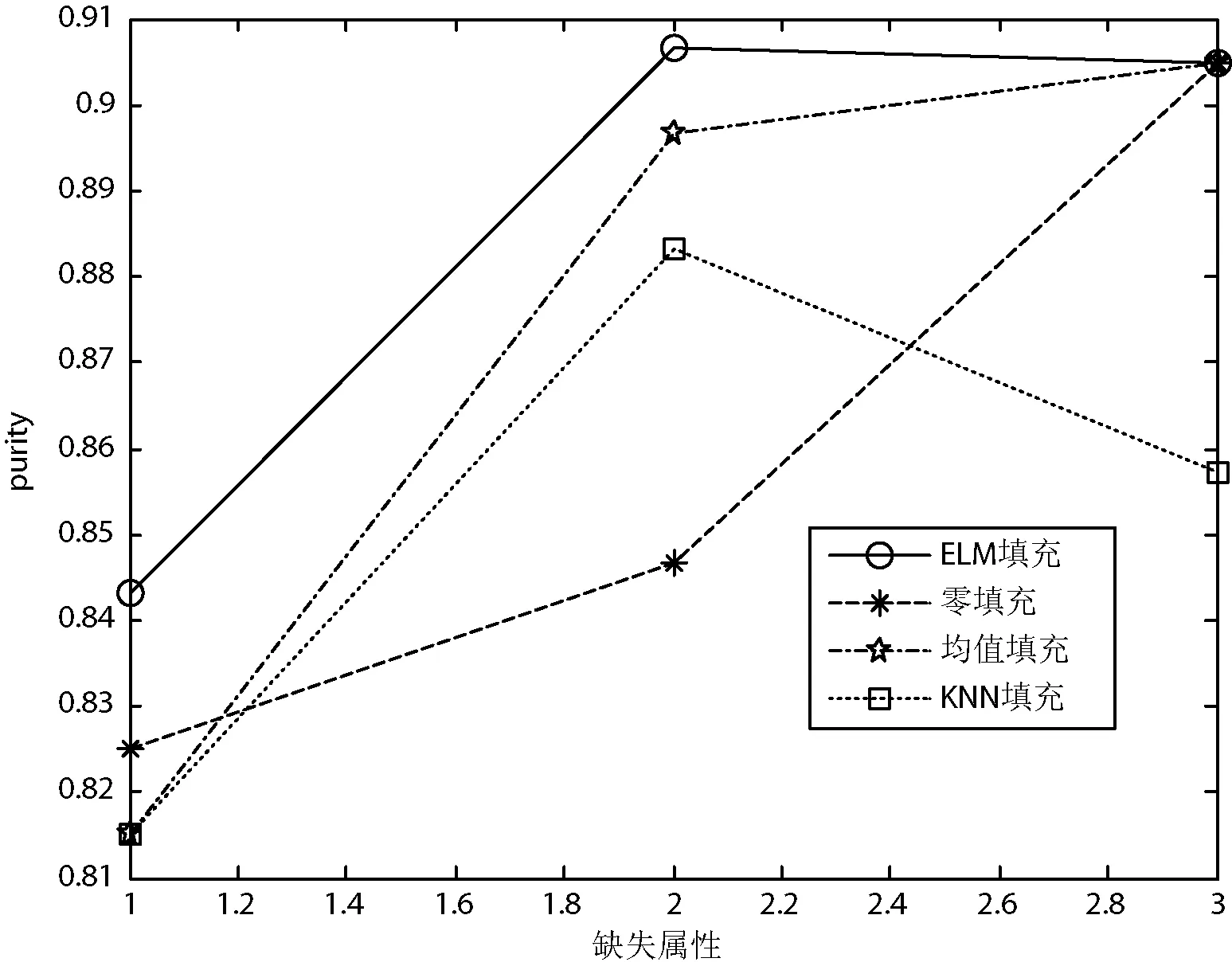
图2　四种填充方法在鸢尾属植物数据集数据集上的聚类纯度比较

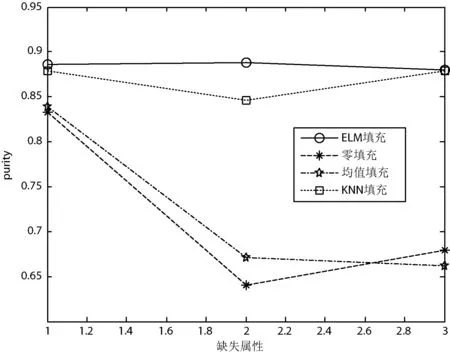
图3　四种填充方法在种子数据集上的聚类纯度比较

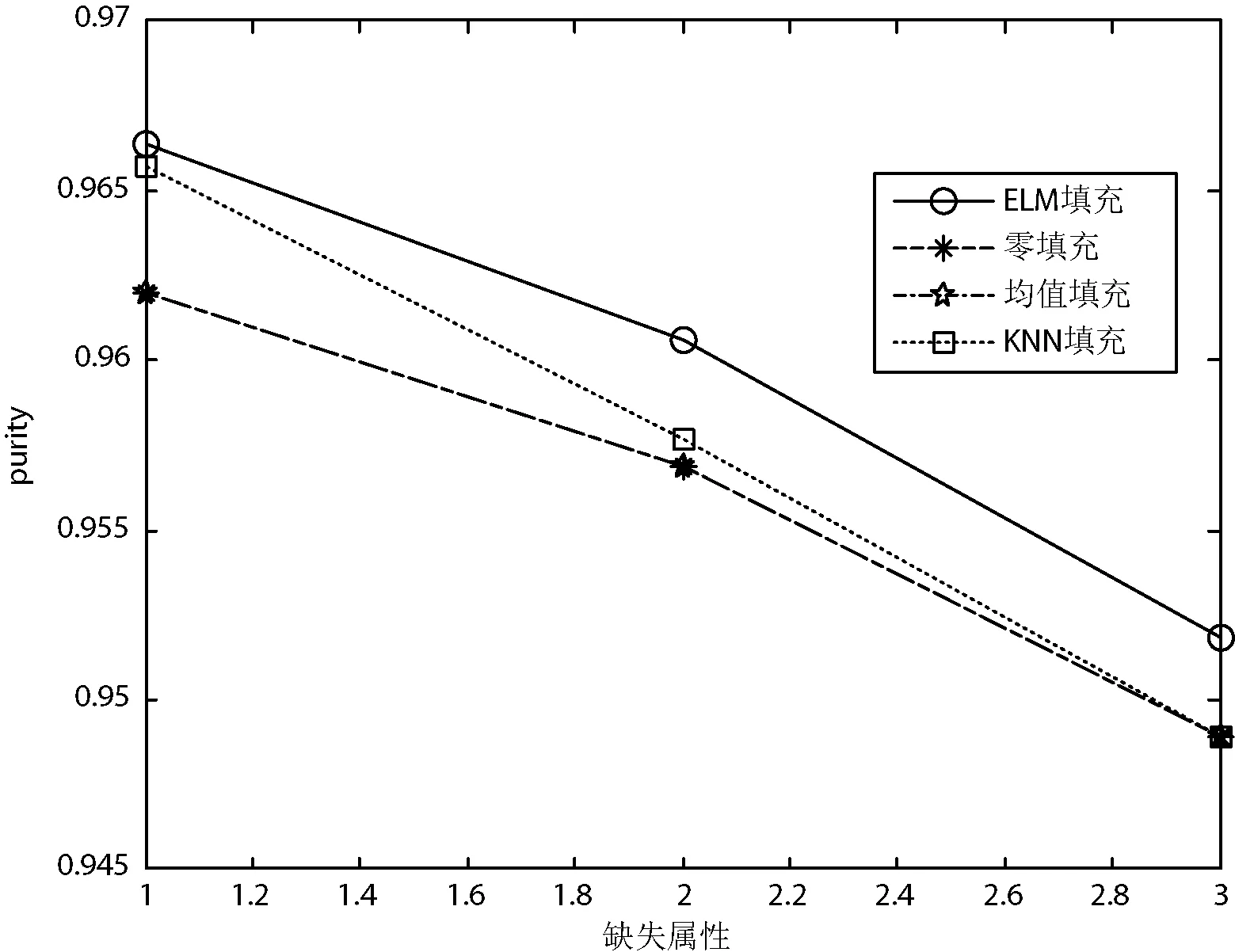
图4　四种填充方法在乳腺癌数据集上的聚类纯度比较

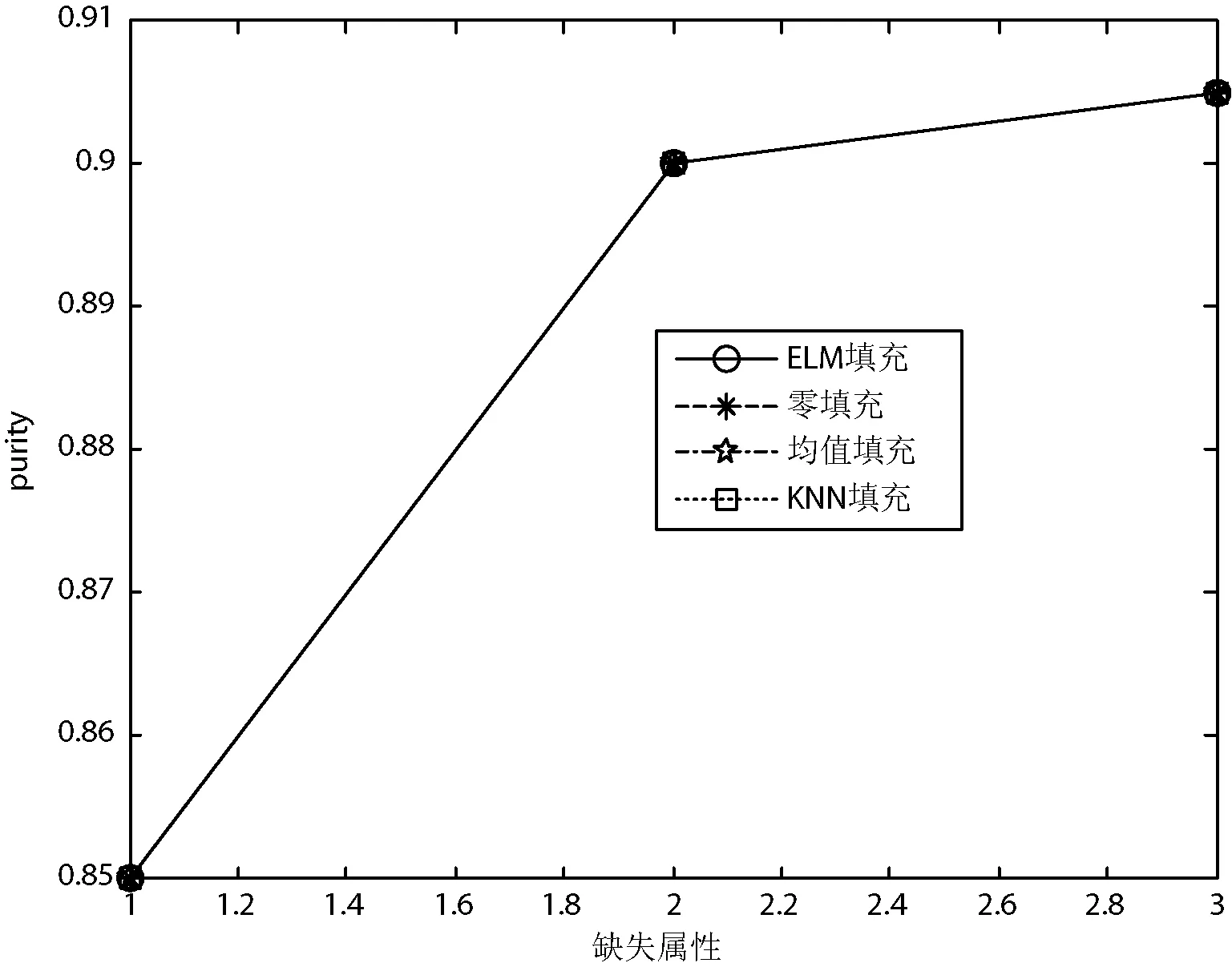
图5　四种填充方法在精液活力数据集上的聚类纯度比较

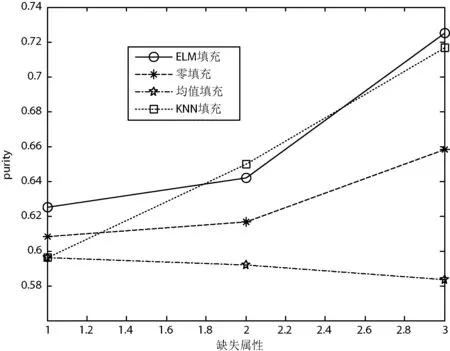
图6　四种填充方法在僧侣问题数据集上的聚类纯度比较

3　结　语

本文提出了一种基于极限学习机的缺失数据填充方法，利用极限学习机建立缺失属性与其他属性之间的非线性映射关系，并利用这种映射关系进行缺失属性填充。 零填充和均值填充执行过程简单、速度较快，但执行过程中没有进行充分的学习，填充效果较差。K近邻填充比零填充和均值填充的填充效果要好，但当样本容量较大时，由于要计算缺失样本中每个样本点与完备样本中每个样本点的欧氏距离，运算量很大，严重影响其运算速度。实验表明，新的填充方法是有效的。

[1] 庞新生.缺失数据处理方法的比较[J].统计与决策,2010(24):152-155.

[2] 金勇进.缺失数据的插补调整[J].数理统计与管理,2001，20(5):47-53.

[3] 何凯涛,陈明,张治国，等.用人工神经网络进行空间不完备数据的插补[J].地质通报,2005，24(5):476-479.

[4] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1-3):489-501.

[5] Huang G B,Chen L.Convex incremental extreme learning machine[J].Neurocomputing,2007,70(16-18):3056-3062.

[6] Ding S F,Zhao H,Zhang Y N,et al.Extreme learning machine:algorithm, theory and applications[J].Artificial Intelligence Review,2015,44(1):103-115.

[7] Huang G B,Zhou H M,Ding X J,et al.Extreme learning machine for regression and multiclass classification[J].Systems, Man & Cybernetics, Part B: Cybernetics, IEEE Transactions on,2012,42(2):513-529.

[8] Zhang L,Zhang Y,Li P.A novel Bio-inspired image recognition Network with Extreme Learning Machine[C]//Proceedings of ELM-2014:Algorithms and Theories,2015,1:131-139.

[9] Dwiyasa F,Lim M H.Extreme learning machine for active RFID location classification[C]//Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems,2015,2:657-670.

[10] Feng L,Wang J,Liu S L,et al.Multi-label dimensionality reduction and classification with Extreme learning machines[J].Journal of Systems Engineering & Electronics,2014,25(3):502-513.

[11] Deng W Y,Zheng Q H,Chen L.Regularized extreme learning machine[C]//IEEE Symposium on Computational Intelligence and Data Mining,2009:389-395.

[12] 邓万宇,郑庆华,陈琳，等.神经网络极速学习方法研究[J].计算机学报,2010,33(2):279-287.

[13] Martínez-Martínez J M,Escandell-Montero P,Soria-Olivas E, et al.Regularized extreme learning machine for regression problems[J].Neurocomputing,2011,74(17):3716-3721.

[14] Yu Q，Miche Y,Eirola E,et al.Regularized extreme learning machine for regression with missing data[J].Neurocomputing,2013,102:45-51.

[15] He Q,Jin X,Du C Y,et al.Clustering in extreme learning machine feature Space[J].Neurocomputing,2013,128:88-95.

[16] Zhao Y P,Wang K K.Fast cross validation for regularized extreme learning machine[J].Journal of Systems Engineering & Electronics,2014,25(5):895-900.

A METHOD FOR MISSING DATA IMPUTATION BASED ON EXTREME LEARNING MACHINE

Yang YiLu Chengbo

(FacultyofEngineeringandDesign,LishuiUniversity,Lishui323000,Zhejiang,China)

In data processing process the problems of having to impute incomplete data are often encountered, so it is important to look for a simple and effective missing data imputation method. In view of this, the paper presents an extreme learning machine-based method for missing data imputation. Based on extreme learning machine modelling it builds a nonlinear mapping model of missing attributes with the need of imputation as well as other attributes. Experimental result shows that the new algorithm has excellent performance in imputation.

Extreme learning machineMissing data imputationUCI machine learning database

2015-04-27。国家自然科学基金项目(11171137)；浙江省自然科学基金项目(LY13A010008)。杨毅，讲师，主研领域：人工神经网络与机器学习。卢诚波，副教授。

TP181TP183

A

10.3969/j.issn.1000-386x.2016.10.054