装备维修过程中备件布局的多目标优化决策

郭　璐　杨　云　王　崴　刘晓卫

(空军工程大学防空反导学院　陕西 西安 710051)



装备维修过程中备件布局的多目标优化决策

郭璐杨云王崴刘晓卫

(空军工程大学防空反导学院陕西 西安 710051)

为保证在装备维修过程中能精确、及时、高效地取用备件，提出备件车装载布局优化问题。针对该问题建立备件布局优化数学模型，以备件车承载容积、载重量及重心等为约束条件，综合考虑备件车空间利用率、备件合重心对行车安全性的影响和备件取用效率为目标函数。根据备件布局模型的特殊性，基于模拟退火算法的思想，将其与带压缩因子的粒子群优化算法结合，应用于实例中求解布局方案，并将此混合算法的计算结果与基本粒子群优化算法的计算结果进行了比较。结果表明，使用混合粒子群优化算法可以获得较好的装载布局优化方案，达到充分利用备件车装载空间、安全性好和取用效率高的目的。

备件车布局粒子群算法模拟退火算法压缩因子

0　引　言

备件车是专门用来装载备件的车辆，其用途主要是给在户外作业发生故障的设备提供维修所需工具及零件，保证其能及时地恢复正常工作[1]。在现代战争环境下，决定战争胜负的因素之一是装备的保障能力。对于导弹装备而言，保障工作的核心就是维修，而装备维修保障的关键就在于保障备件的及时供应[2]。因此，在有限空间内，如何对备件进行布局，能否精确、迅速地取用备件决定着装备的维修保障能力，这是装备维修保障工作的重难点[3]。

备件车装载布局是将复杂繁多的备件装载到备件车有效空间内以及将备件存放位置在此空间内布置。此问题属于NP[4]难问题，约束条件复杂，目标函数多，采用确定性优化算法求解时不易获得理想的结果甚至有时得不到结果。鉴于此，对于NP

难问题，很多学者采用群智能优化算法求解。文献[5]采用空间分割方法建立了三维布局模型，运用蚁群算法对三维混合布局优化问题优化进行求解，得到了最优解。随着智能算法越来越受到广大学者关注与研究，部分学者将多种智能算法混合求解装载布局问题。文献[6]为解决设备布局这一典型的NP难问题，提出将模拟退火方法与粒子群算法有机结合，使算法全局搜索能力增强。也有很多学者对群智能算法进行改进，以弥补部分算法较易陷入局部最优的缺陷或者使算法收敛速度更快。文献[7]针对面积不同但形状固定的设备的布局问题，提出了改进的遗传算法，实现了算法参数的非线性自适应调整，实例仿真表明，此算法可以较快地获得所求问题的近似最优解。

本文提出了混合粒子群优化算法PSO(particle swarm optimization)解决备件车装载布局问题。PSO算法[8]凭借其操作流程简单、收敛速度快等特点在组合优化问题上独树一帜，但其缺陷也是不容忽视的，即其在寻优过程中全局搜索能力不强，较易陷入局部极值。为此，本文在已有算法及各种改进算法的启发下，将有突跳能力、能够有效避免搜索过程陷入局部最优的模拟退火SA(simulated annealing)算法[9]与PSO算法很好地融合在一起来求解备件车布局优化问题。

国内外研究备件车的文献比较少，在类似问题上已有不少相关研究成果。主要的研究关注对布局空间利用率的提升上，对于待布备件重心的约束与优化较少，鲜有考虑提高待布备件取用效率的问题。根据备件车装载的一般性及特殊性，对于备件车装载布局的研究既要参考一般货物装载布局设计又要借鉴人机工效。因此，本文充分考虑备件车空间利用率、备件车行车安全性和备件取用效率，对备件建立多目标布局优化模型，采用混合粒子群优化算法求解数学模型，得到备件装载布局的优化方案。

1　备件布局优化模型

本文采用提取备件最小组合包络矩形块的方法对备件进行简化处理。处理完成后，备件即为大小各异的矩形块。设有N个待布备件，pi表示第i个备件，i=1,2,…,N，qi和vi分别为备件pi的重量和体积；L、W和H为备件车的长、宽和高；Q和V分别表示备件车最大载重量和最大可用空间。进行布局前，先建立笛卡尔坐标系，以备件车内左前下角为坐标原点，X轴从原点出发，沿备件车底板侧边，平行于备件车底板纵中心线；Y轴从原点出发，沿备件车端，平行于备件车底板横中心线；Z轴从原点出发，垂直于备件车底板平面。如图1所示。

图1　备件车坐标系

基于此，分别考虑备件车空间及载重约束、备件车行车安全性及备件取用效率这三方面因素建立布局优化数学模型。

1.1基于备件车空间及载重约束的数学模型

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

i=1,2,…,Nj=1,2,…,Ni≠j

(10)

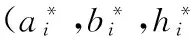
目标函数表示使备件车空间利用率最大。约束条件中，式(2)—式(4)为备件布局的不干涉约束，表示备件在布置时互不重叠；式(5)—式(7)为备件车的边界约束，表示备件布局时不允许超出备件车的边界；式(8)为载重约束，表示装载备件的总重量不允许超过备件车的最大载重量；式(9)为容积约束，表示装载备件的总体积不允许超过备件车的有效容积。

1.2基于备件车行车安全性的数学模型

(11)

(12)

(13)

(14)

式(11)—式(14)中，(Cx,Cy,0)为车底板纵横中心线交叉点坐标；Δy为备件合重心的横向容许偏移量；Δx为备件合重心的纵向容许偏移量；Δz为备件合重心的最大允许高度(以备件车底板为起始面)。

目标函数表示使备件的合重心偏移量最小。约束条件中，式(12)—式(14)为合重心约束，表示备件车中的备件的合重心偏移量必须在规定的范围内。

1.3基于备件取用效率的数学模型

人机工效布局原则是进行布局设计的依据，本文依照备件布局的特殊性，选取备件的重要性、使用频率、以及备件相关性等设计原则对基于备件取用效率的备件车进行布局研究。根据人在备件车内手部的操作范围、人眼的视野范围及人存取备件需要行走的距离(备件距离备件车门的距离)，来评判备件位置的优劣，并对备件进行排序。综合考虑这三个因素，将人手操作最舒适、人眼最易注意到且距离车门最近的位置的备件排列在最前面，位置次之的备件接连排列，直到位置最次的备件排列完成。对于N个需要布局的备件，可组成有序序列X={x1,x2,…,xn}，x1,x2,…,xn∈pi，i=1,2,…,N。本文结合以下人机工效布局原则，建立备件取用效率评价的数学模型。

(1) 重要性原则

重要性原则是指根据备件的重要程度大小，把重要的备件布置在备件车内易于取用的位置。对于取用者来讲，重要度高的备件应该布置在操作者手部最适宜存取区域内或者操作者视野的最佳范围内或者存取所需移动的距离最短的位置。

在备件的布局序列中，重要性越高的备件则在布局序列中越靠前。备件pi的重要性权值用Pmi表示，由此构造备件重要性子目标函数：

(15)

由式(15)意义可知，f1(X)值越大表示序列X={x1,x2,…,xn}越符合重要性原则。

(2) 使用频率原则

使用频率原则是指将维修过程中使用次数多的备件布置在便于寻找和存取的位置，提高取用的速度和准确性，并减轻维修人员的生理和心理负担。

对于使用频率的量化可采用统计方法，备件pi的使用频率权值用Fri表示。使用频率越高的备件在布局序列中的位置越靠前，由此得使用频率子目标函数：

(16)

由式(16)可知，f2(X)值越大表示序列X={x1,x2,…,xn}越符合使用频率原则。

(3) 相关性原则

在维修过程中，有些备件需要与其他备件协同使用来完成维修任务，这些备件具有相关性，相关性是备件布局中需考虑的重要原则。备件pi与pj的相关性大小用Rexixj表示，相关性参数进行归一化处理，数值越大表明备件相关性越大。备件间相关性系数如表1所示。

表1　备件相关性

两备件间相关性越大，在布局序列中的位置越靠近，由此可得相关性子目标函数：

(17)

由式(17)可知，f3(X)值越大表示序列X={x1,x2,…,xn}越符合相关性原则。

(4) 目标函数

综合考虑上述三种布局原则及各原则之间的关系，通过加权法将以上三个子目标函数组合，可构建如下备件布局优化目标函数：

maxF(X)=ω1f1(X)+ω2f2(X)+ω3f3(X)

(18)

式(18)中，ωi(i=1,2,3)为各子目标函数的权重系数，可根据维修任务及待装备件的特点对子目标权重值加以调整，以适应实际的需求。

1.4备件车装载布局优化的数学模型

本文所研究的备件车装载布局优化问题属于多目标优化问题，因此先根据不同的约束或者原则对各目标函数进行分步设计，最终采用加权法确定最终目标函数。综合考虑备件车空间及载重约束、备件车行车安全性及备件取用效率这三方面因素，可建立约束条件为式(2)—式(9)及式(11)—式(13)、目标函数如式(18)的布局优化数学模型：

(19)

式(19)中的权重系数α为备件车空间利用率权重系数，β为备件合重心位置偏移量权重系数，γ为备件存取效率权重系数。目标函数中，第1项为备件车空间利用率，第2项为备件合重心位置偏移量，第3项为备件存取效率。

2　备件布局的混合粒子群算法求解过程

2.1基于模拟退火的粒子群优化算法

基于模拟退火SA的粒子群算法中的粒子群算法采用带压缩因子的粒子群优化算法CFPSO(Constrict Factor Particle Swarm Optimizer)，CFPSO算法通过选取合适参数，可确保算法的收敛性。算法中速度和位置更新公式如下：

vi,j(t+1)=χ[vi,j(t)+c1r1(pi,j(t)-xi,j(t))+

c2r2(pg,j(t)-xi,j(t))]

(20)

xi,j(t+1)=xi,j(t)+vi,j(t+1)j=1,2,…,d

(21)

vi,j(t+1)=χ[vi,j(t)+c1r1(pi,j(t)-xi,j(t))

(22)

(23)

2.2应用混合粒子群算法的备件车布局

(1) 粒子群初始化

在备件车布局优化过程中，假设备件车要装载D个矩形块备件，一个微粒表示一种布局方案，则每个微粒的编码是一个3D维向量P=(x1,…,xd,y1,…,yd,z1,…,zd)，前面、中间及后面D维分别表示备件重心的X坐标、Y坐标及Z坐标；每个粒子的行进方向和飞行速率也是一个3D维向量V=(vx1,…,vxd,vy1,…,vyd,vz1,…,vzd)，前面、中间及后面D维分别表示备件在X方向、Y方向及Z方向的移动速度。每个微粒的位置根据式(20)和式(21)进行变换。

(2) 适应度函数

针对此备件车布局，适应度函数可表示为F=maxZ。由此可知，适应度值越大，目标函数值越大，求得的布局方案越满足要求。

(3) 停止规则

算法运行之前会设定一个迭代次数，若算法运行到最大迭代次数，则迭代结束，退出程序；或者算法运行到一定程度，适应度函数值连续迭代30步保持平稳，则停止循环，退出程序。退出后即可得到适应度值最优的布局结果。

2.3问题求解和算法流程设计

SA-PSO算法寻优步骤如下：

步骤1随机初始化微粒的位置和速度。

步骤2计算种群中每个微粒的适应度fitness，并寻找粒子的pbest和gbest。

步骤3重复执行以下步骤。

① 对粒子的pbest进行SA邻域搜索，初始化退火温度Tk(k=0)。

③ 退火操作：Tk+1=CTk,k←k+1，其中C∈(0,1)。若满足收敛判据，则退火过程结束；否则，转②。

步骤4根据改进的更新方程式(22)和式(21)来调整粒子的速度和位置，并更新粒子的pbest。

步骤5执行最优选择操作，更新种群gbest。

步骤6判断gbest是否满足算法终止准则，若满足，则输出全局最优解；若不满足，返回到步骤3。

3　算例分析

本文以备件车为背景，求解备件的3维正交布局方案，抽取16组待布备件，备件重要性权值、使用频率权值及其相关性系数如表2和表3所示。设定备件布局优化数学模型中重要性权重系数w1=0.2，使用频率权重系数w2=0.5，相关性权重系数w3=0.3；设定优化算法种群规模sizepop=50，学习因子c1=c2=2，最大迭代次数M=1000；退火初始温度退火温度T0=1000，衰减因子C=0.5。

表2　待布备件重要性及使用频率权值

表3　待布备件相关性

由于对备件进行布局设计需综合考虑备件车空间利用率、备件合重心对行车安全性的影响和备件取用效率，故在维修任务及外界环境因素不同的情况下备件布局优化数学模型参数设置不同。若备件繁多，备件车空间有限，需重点考虑备件车空间利用率的问题，则权重系数α取值较大；若备件车行车路况恶劣，需保证备件车行车安全性，则权重系数β取值较大；若备件车空间较大，行车路况良好，在维修过程中需精确、快速地取用备件，则权重系数γ取值较大。下面设计三种备件布局模型：(1)侧重考虑备件车空间利用率，取权重系数α=0.6，β=0.2，γ=0.2；(2)侧重考虑备件车行车安全性，取权重系数α=0.2，β=0.6，γ=0.2；(3)侧重考虑备件取用效率，取权重系数α=0.2，β=0.2，γ=0.6。采用SA-PSO算法求解布局模型，进行了10次计算，对求解结果取平均值如表4所示。由表4可以看出，方案一的布局结果备件车空间利用率最大；方案二的布局结果备件合重心偏移最小，备件车行车安全性最高；方案三的布局结果备件取用效率最高。三种布局结果均符合外界环境及维修任务的需求。

采用标准PSO算法求解布局模型，进行了10次计算，选取布局模型三的一次求解过程如图2所示。由图2可知，本文的SA-PSO算法能搜索到全局最优点，且找到最优解的速度更快。观察10次平均求解过程及结果如表5和表6所示。根据SA-PSO算法求得的布局结果，画出备件最优布局位置如图3所示。

图2　SA-PSO算法与PSO算法迭代过程

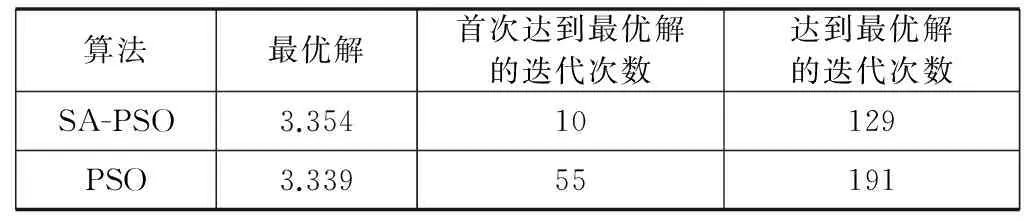
算法最优解首次达到最优解的迭代次数达到最优解的迭代次数SA-PSO3.35410129PSO3.33955191

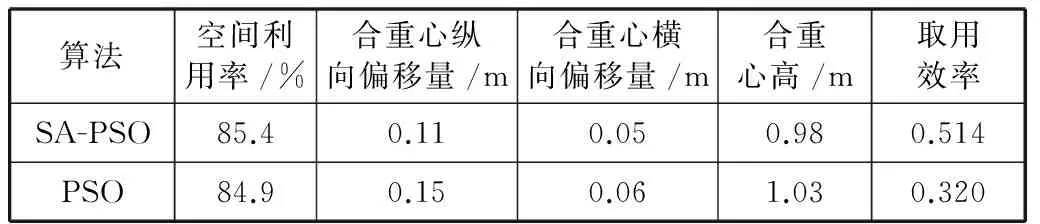
表6　SA-PSO算法与PSO算法结果对比

图3　备件布局位置

4　结　语

本文提出一种SA-PSO算法用于求解备件车装载布局优化问题。由于基本PSO算法容易陷入局部最优，故采用了CFPSO算法，压缩因子能有效地避免所以粒子均飞向局部极值点，增强了算法的局部寻优能力，这种调整方式只需选取合适的参数，就可保证PSO算法收敛。SA算法在寻优过程能有效地避免陷入局部极值，在一定条件下一定能收敛于全局最优解。SA-PSO算法在优化过程中以依照突跳概率接受接近全局极值的次优解，避免陷入局部极值，实现了全局寻优。从理论分析及布局优化实例结果可以看出，本文提出的SA-PSO算法用来解决备件车布局问题时，能综合考虑备件车空间利用率、备件合重心对行车安全性的影响和备件取用效率，得到较好的布局结果。

[1] 张蕊，袁立峰，汪凯蔚.备件优化理论分析与应用研究[J].装备环境工程，2012，9(5)：52-55.

[2] 王明亮，余勃彪.装甲装备器材仓库备件库存优化方法[J].兵工自动化，2013，32(8)：21-24.

[3] 田继亮.设备维修过程中备件管理多目标优化技术研究[D].西安：西安电子科技大学，2013.

[4] Garey M R，Johnson D S.Computer and Intractability：A guide to the Theory of NP-Completeness[M].New York：Freeman，1979：16-20.

[5] 张泓，李爱平，刘雪梅.基于多目标改进蚁群算法的三维混合布局方案设计[J].农业机械学报，2010，41(7)：191-197.

[6] 祝恒云，叶文华.模拟退火粒子群算法在动态单元布局中的应用[J].中国机械工程，2009，20(2)：181-185.

[7] 周娜，宓为建，徐子奇，等.基于改进型自适应遗传算法求解设备多行布局问题[J].上海交通大学学报，2013，47(12)：1924-1929.

[8] Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proc of IEEE Int’l Conf Neural Networks.Los Alamitos，CA：IEEE Computer Society Press，1995：1942-1948.

[9] Szykman S，Cagan J.A simulated annealing-based approach to three-dimensional component packing[J].Transaction of ASME，1995，117：308-314.

[10] 王正元,曹继平,朱昱,等.考虑维修能力的战时备件资源配置方法研究[J].兵工学报,2014,35(5)：719-724.

[11] 杨仕美,石忠义,翟旭升,等.基于重要度的航材备件库存综合优化模型[J].火力与指挥控制,2014,39(8)：109-113.

[12] 郭源源，王谦，梁峰.基于粒子群优化算法的车间布局设计[J].计算机集成制造系统，2012，18(11)：2476-2484.

[13] 刘衍民.一种求解约束优化问题的混合粒子群算法[J].清华大学学报:自然科学版，2013，53(2)：242-246.

[14] 范文,余隋怀,王文军,等.蚁群算法求解人机布局优化问题[J].机械科学与技术,2013,32(7)：955-962.

[15] Wu Hao，Zuo Hongfu.Using genetic /simulated annealing algorithm to solve disassembly sequence planning[J].Journal of Systems Engineering and Electronics，2009，20(4)：906-912.

[16] 王帅旗.船舶驾驶室布置人机工程设计及其应用[D]哈尔滨：.哈尔滨工程大学，2013.

MULTI-OBJECTIVE OPTIMISATION DECISION FOR SPARE PARTS LAYOUT IN EQUIPMENT MAINTENANCE PROCESS

Guo LuYang YunWang WeiLiu Xiaowei

(SchoolofAirDefenseandAnti-missileInstitute,AirForceEngineeringUniversity,Xi’an710051,Shaanxi,China)

In order to ensure accurate,timely and efficient spare parts access in equipment maintenance process,we put forward the problem of loading and layout optimisation for spare parts car.In light of this issue we built the mathematical model of spare parts layout optimisation,took the bearing volume,load capacity and gravity centre of the spare car as the constraint conditions,and took into account comprehensively the space utilisation of spare parts car,the influence of spare parts’ combined gravity centres on driving safety and the spare parts’ access efficiency as the objective functions.According to the particularity of spare parts layout model and based on the idea of simulated annealing algorithm,we combined them with the particle swarm optimisation with constrict factor and applied it in actual example to calculate the layout solution.We also compared the calculation result of this hybrid algorithm with that of the basic particle swarm optimisation algorithm.Results showed that to use hybrid particle swarm optimisation algorithm can obtain better loading and layout optimisation scheme,it achieves the goals of making full use of spare car’s loading space,good in safety and high access efficiency.

Spare carLayoutParticle swarm optimisationSimulated annealing algorithmConstrict factor

2015-07-03。国家自然科学基金项目(51075395);国家高技术研究发展计划项目(2013AA040604)。郭璐，硕士生，主研领域：机械结构优化设计。杨云，副教授。王崴，副教授。刘晓卫，讲师。

TP311

A

10.3969/j.issn.1000-386x.2016.10.052