二级推理在图像去噪中的应用
2016-11-08胡晓辉
方 政 胡晓辉 陈 永
(兰州交通大学电子与信息工程学院 甘肃 兰州 730070)
二级推理在图像去噪中的应用
方政胡晓辉陈永
(兰州交通大学电子与信息工程学院甘肃 兰州 730070)
对图像去噪的方法进行了研究,针对传统去噪方法对所有像素点进行去噪处理造成的图像模糊化问题,提出一种基于贝叶斯决策的二级推理模型。首先建立基于贝叶斯决策的二级推理模型,通过图像的灰度直方图,获得贝叶斯决策所需要的参数。首次推理判断之后,对获得的分类进行第二次推理判断,最终获得噪点与非噪点的分类。再将二级推理模型与三种去噪算法进行结合,对图像进行去噪测试。通过实验验证,提出的算法能有效地在尽可能去除图像噪声的情况下,最大程度地保留原图像的细节,改善了以往图像去噪算法中去噪后图像模糊化较为明显的情况。
图像去噪二级推理贝叶斯决策模糊化
0 引 言
现实中的数字图像[1]在数字化和传输过程中常受到成像设备与外部环境噪声干扰等影响,形成带有噪声的图像。而图像去噪就是将数字图像中噪声减少乃至去除的过程。传统的去噪方法都是直接对待处理的图像进行去噪等操作,这使得很多图像中的非噪点也经过了去噪处理,造成了图像细节的丢失,图像的模糊化较为明显。因此,需要一种较为有效的方法,在对图像进行去噪处理之前,对非噪点和噪点进行区分,使得后续的去噪处理更有针对性,从而获得更具有细节、更为清晰的去噪图像。贝叶斯决策的特点正好符合以上要求。
已经有不少学者对于贝叶斯决策理论在图像处理中的应用进行了一些工作:包晓敏等[2]提出了一种基于最小风险贝叶斯决策的图像分割方法,将目标图像和非目标图像作为两个类别进行判别,得到了较为准确的图像分割结果;杨会云等[3]结合Bayes理论和邻域平均法,提出一种基于均值滤波和最小错误率贝叶斯决策的去噪方法,实现了去噪同时保留图像细节;胡觉亮[4]提出了基于贝叶斯决策理论的织物图像自动分类的新方法,通过提取织物图像的形态结构参数作为特征向量, 并计算出分类结果;葛琦等[5]提出了基于贝叶斯分类模型的双水平集分割算法,提高了分割效率,实现了大脑图像的分割;张鑫等[6]提出一种基于正态反高斯模型的贝叶斯图像去噪方法,以正态反高斯模型为先验模型,对图像小波系数的稀疏分布统计建模,并用最大后验概率估计法对小波系数进行估计,可以提高图像的峰值信噪比值;郭小燕等[7]提出基于多级推理的专家系统,采用多级推理机制,降低推理结果的数量,提高了推理的准确性。
本文提出一个基于贝叶斯决策的二级推理模型。利用该模型对三种传统图像去噪算法进行改进,即在图像去噪前,利用基于贝叶斯决策的二级推理模型,将噪点与非噪点进行初步划分,之后再结合去噪方法,对图像进行去噪处理。
1 基于贝叶斯决策的二级推理模型
1.1二级推理
推理是由一个或几个已知的前提,推导出一个未知结论的思维过程。二级推理是利用对同一事物,在进行初次推理之后,再次对其进行推理获得结论的过程。进行推理时,根据初期获得的证据作出初次推理。由于用于初次推理的证据较少,出现差错的偶然性误差较大,可以采用后期获得的证据进行二级推理,从而提高推理所得到的结果的准确性。
贝叶斯决策[8,9]指的是在情况不完全掌握的条件下,采用主观概率估计的方法,对部分未知的状态进行推测;然后再利用贝叶斯公式对事件发生的概率进行修正;最后再利用期望值和修正概率来做出最优决策。
贝叶斯决策主要是通过以下三步来实现:
1) 已知类条件概率密度参数表达式和先验概率。
2) 利用贝叶斯公式转换成后验概率。
3) 根据后验概率大小进行决策分类。
本文采用的二级推理方法,主要是利用贝叶斯决策理论来进行推理的。首先根据已知类条件概率密度参数表达式和先验知识进行初次推理;然后利用贝叶斯公式转换成后验概率,利用后验概率进行决策分类;而第二次推理时,对第一次划分的两个分类中的目标再次利用贝叶斯决策进行推理,最终得到更为准确的结果。
1.2基于贝叶斯决策的二级推理模型的建立
去除噪声过程中,一般来说,总是希望去除尽可能多的噪点,但在尽量去噪的同时又存在着去噪过度的可能性,这就出现了二者之间的一个矛盾点。为了将误差值降到最小,可以在去噪之前,利用二级推理对像素进行分类,提高像素点中噪点和非噪点的分类准确度,最大化算法处理像素点是噪点的概率。本文所提出的二级推理模型是建立在贝叶斯决策理论的基础上,利用先验知识和后验知识进行两次推理,得到最终的结论。
贝叶斯决策是利用贝叶斯公式的特点,针对各类问题,以概率的大小作为依据,对目标进行分类,最大程度减少错误的分类,得出分类规则。
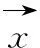
在获得了观测向量的各种参数之后,就可以依据这些参数,进行一次基于概率的推理:
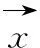
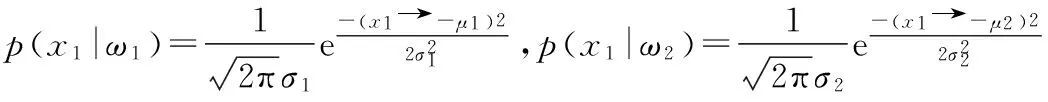
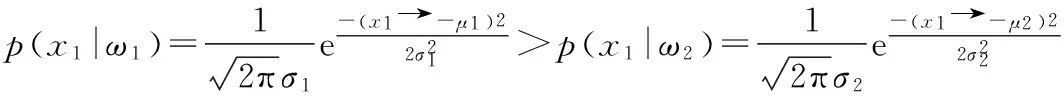
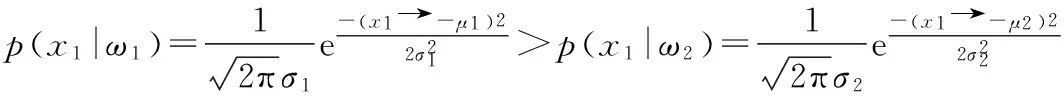
ω1类为噪点类,ω2类为非噪点类。
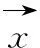
其中:
(1) ω1类中依然划分为噪点的记为ω11;
(2) 初次划分为ω1,而第二次划分为非噪点的记为ω12;
(3) ω2类中初次划为非噪点而第二次划分为噪点的记为ω21;
(4) 两次均划分为非噪点的记为ω22。
由于ω21和ω12都有经过推理被划分为噪点的经历,为防止遗漏噪点,因此将它们并入ω1,都利用中值去噪算法进行处理。
根据上述规则,如果出现:
p(ω11|x2)>p(ω12|x2);
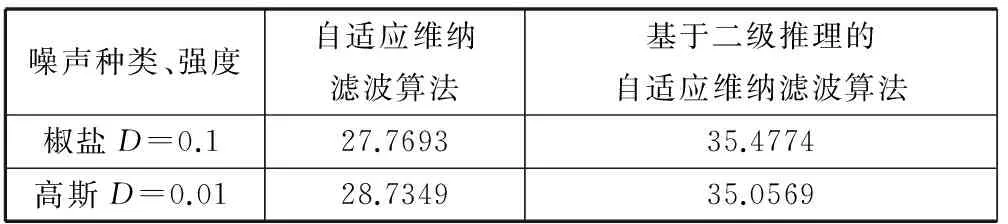
p(ω11|x2) p(ω21|x2)>p(ω22|x2); 以上这三种情况,则统一把该像素点归类为ω1;若有p(ω21|x2) 第二次推理时的条件概率密度计算方法与第一次推理的计算方法相一致。结合两次推理的分类情况,就可以在对图像去噪之前,将噪点与非噪点基本上分离开来,在提高去噪准确度的同时,也可以提高对图像的处理效率。 本文将二级推理模型分别与三种经典去噪算法相结合,应用到图像去噪中,并进行测试和分析。 2.1基于二级推理和中值滤波的去噪算法 中值滤波[10]是一种经典滤波算法,其核心思想是对每个像素的邻域像素进行排序后取中值。而基于二级推理和中值滤波的去噪算法,只对判定为噪声的点进行排序处理,这样就可避免使图像整体变模糊。算法基本步骤如下: (2) 利用贝叶斯决策对噪点和非噪点进行首次推理判断。 若存在: 同理,若存在: (3) 再次利用贝叶斯决策准则对首次分类后的噪点和非噪点进行第二次推理判断。 (4) 对判定为噪声的点,使用中值滤波法进行处理。 2.2基于二级推理和均值滤波的去噪算法 均值滤波[12]是一种典型的线性滤波算法,其核心思想是在图像上对目标像素给出一个包括了其周围的临近像素模板,再以模板中全体像素的平均值来代替原来像素值,从而达到滤波的目的。将基于贝叶斯决策的二级推理模型与均值滤波的去噪算法,通过两次贝叶斯决策推理,确定出噪点和非噪点。然后对判定为噪声的点进行均值滤波处理,可以在最大程度保留图像细节的同时进行去噪。 算法的具体步骤中,前三步与2.1节中基于二级推理和中值滤波的去噪算法的步骤(1)-步骤(3)步一样,只有第四步改用均值滤波算法进行处理,在此不再赘述。 2.3基于二级推理和自适应维纳滤波的滤波算法 自适应维纳滤波[13]也是一种典型的线性滤波算法,其核心思想是以均方误差最小为准则,以图像的局部方差作为参数,调整滤波器的输出,局部方差越大,平滑效果越好。采用基于贝叶斯准则的二级推理模型与其相结合,可以得到新的自适应维纳滤波算法。算法的具体步骤中,前三步与2.1节中基于二级推理和中值滤波的去噪算法的步骤(1)-步骤(3)步一样,只有第四步改用自适应维纳滤波算法进行处理,在此也不再赘述。 2.4测试 以数字图像处理领域中的经典图像莱娜图作为测试图像,分别进行算法测试: (1) 对莱娜图添加不同强度的椒盐噪声,通过中值滤波算法以及基于二级推理的中值滤波算法分别进行滤波,方差D=0.05、D=0.1的椒盐噪声得到的结果分别如图1和图2所示。 图1 D=0.05时,对椒盐噪声的处理结果 图2 D=0.1时,对椒盐噪声的处理结果 (2) 对莱娜图添加不同强度的高斯噪声,通过传统均值滤波算法以及基于二级推理的均值滤波算法分别进行滤波,方差D=0.005、D=0.01的高斯噪声,得到的结果分别如图3和图4所示。 图3 D=0.005时,对椒盐噪声的处理结果 图4 D=0.01时,对椒盐噪声的处理结果 (3) 分别对添加了D=0.1的椒盐噪声和D=0.01的高斯噪声的莱娜图,利用自适应维纳滤波算法、基于二级推理的自适应维纳滤波算法分别进行滤波,得到的结果分别如图5所示。 2.5结果分析 考虑人眼视觉的差异性,本文采用视觉评判和信噪比定量分析来对结果作出分析。本文采用图像评判标准中常用的峰值信噪比[14]PSNR作为评判标准。 峰值信噪比是一种评价图像的客观标准,该方法的原理是通过计算原始图像以及经过处理的图像之间的均方误差,相对于(2n-1)2的对数值(信号最大值的平方,n是每个采样值的比特数),峰值信噪比的单位为dB。 峰值信噪比的计算公式为: (1) 其中,MSE为原始图像与经过处理图像之间的均方误差。 2.4节中,三种去噪算法所得结果的PSNR经过测定,分别如表1-表3所示。 表1 中值算法和改进中值算法信噪比 表2 均值算法和改进均值算法信噪比 表3 自适应维纳滤波算法和改进自适应维纳滤波算法信噪比 从视觉效果上看,基于二级推理的算法与传统算法相比较,图像细节保留效果更好。 而在信噪比方面,通过表1-表3可以看出:无论是椒盐噪声还是高斯噪声,经过改进的算法的处理所得到的信噪比,比传统算法的信噪比均有了一定的提升。 综合看来,本文提出的算法,在图像的细节保留、信噪比等方面,都获得了较好的效果。无论对于椒盐噪声,还是高斯噪声,本文的二级推理模型与具体算法相结合得到的新算法的去噪效果,都优于传统算法。 通过以上实验和分析可以看出,在图像去噪之前,采用二级推理的方法对图像进行预处理,可以有效地将像素中的噪点和非噪点分离开来。之后再采用去噪算法进行去噪处理,能够保证去除噪点的同时,绝大部分非噪点的像素不受影响。本文提出的基于贝叶斯决策的二级推理模型与具体去噪算法相结合,能够在去噪的同时最大程度地保留原图像的细节,图像去噪后图像模糊化的情况得到了改善,说明了算法的有效性。 同时,在利用二级推理对图像进行预处理时,尽管可以保证大部分非噪点不受影响,但是仍然存在误分类的情况,导致图像去噪效果并不是特别好。这是因为参数的选取是从直方图中通过估计所得到的,存在一定的误差,从而导致最后的推理结果出现了传递误差。因此需要在不同情况下根据实际情况进行修改和调整,进一步提高分类的准确性。 [1] 冈萨雷斯,伍兹.数字图像处理[M].3版.阮秋琦,等译.北京:电子工业出版社,2011. [2] 包晓敏,汪亚明.基于最小风险贝叶斯决策的织物图像分割[J].纺织学报,2006,27(2):33-36. [3] 杨会云,张有会,霍利岭,等.Bayes理论和邻域平均法在图像去噪中的应用[J].计算机工程与应用,2010,46(9):149-151. [4] 胡觉亮.基于贝叶斯方法的织物分类研究[J].纺织学报,2004,25(1):48-49. [5] 葛琦,张建伟.基于贝叶斯分类模型的双水平集算法的大脑图像分割[J].计算机应用与软件,2009,26(8):64-66,72. [6] 张鑫,井西利.一种基于正态反高斯模型的贝叶斯图像去噪方法[J].光学学报,2010,30(1):70-74. [7] 郭小燕,王联国.基于多级推理的玉米病虫害专家系统[J].自动化与仪器仪表,2013(6):134-137. [8] Stirling W C,Morrall D R.Convex Bayes decision theory[J].IEEE Transactions on Systems,Man and Cybernetics,1991,21(1):173-183. [9] Marc Lebrun,Antoni Buades,Jean-Michel Morel.Implementation of the “Non-Local Bayes” (NL-Bayes) Image Denoising Algorithm[J].Image Processing On Line,2013,3:1-42. [10] 周华.基于动态窗口的自适应中值滤波算法[J].计算机应用与软件,2011,28(7):141-143,166. [11] 周奇,张永光,徐健健.基于直方图特性的图像去噪方法[J].电子测量技术,2007,30(1):40-42. [12] 朱士虎,游春霞.一种改进的均值滤波算法[J].计算机应用与软件,2013,30(12):97-99,116. [13] 易三莉,贺建峰.基于BEMD与自适应维纳滤波的图像降噪[J].计算机工程与应用,2013,49(10):156-158,231. [14] 王敏,周磊,周树道,等.基于峰值信噪比和小波方向特性的图像奇异值去噪技术[J].应用光学,2013,34(1):85-89. APPLYING TWO-LEVEL INFERENCE IN IMAGE DENOISING Fang ZhengHu XiaohuiChen Yong (SchoolofElectronicandInformationEngineering,LanzhouJiaotongUniversity,Lanzhou730070,Gansu,China) In this paper we research the method of image denoising. For the problem of image blurring of traditional denoising method caused by executing denoising process on all pixels, we proposed a Bayesian decision-based two-level inference model. First, we built a Bayesian decision-based two-level inference model, and obtained the parameters required by Bayesian decision through greyscale histogram of image. After the first inferring, we carried out secondary inference on the obtained classification, and finally acquired the classification of noise and non-noise points. Then we combined the two-level inference model with three kinds of denoising algorithms to test the ability of image denoising. It is verified through experiments that the algorithm proposed in this paper can effectively retain the details of original image to maximum extent under the condition of removing image noise as much as possible, this improves the situation in previous image denoising algorithm that the image blurring becomes rather significant after denoising. Image denoisingTwo-level inferenceBayesian decisionBlurring 2015-03-19。国家自然科学基金项目(61163009);甘肃省科技支撑计划项目(144NKCA040);甘肃省教育厅科研项目(1104 05)。方政,硕士生,主研领域:图像处理,智能信息处理。胡晓辉,教授。陈永,博士。 TP391 A 10.3969/j.issn.1000-386x.2016.10.0432 基于二级推理模型的去噪算法
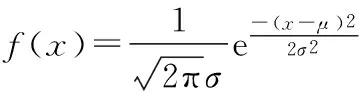
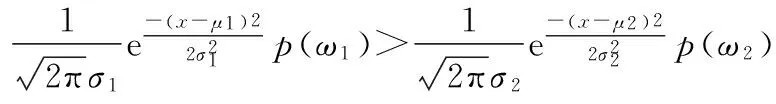
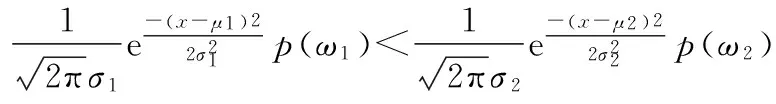






3 结 语
