基于Curvelet变换的压缩传感超分辨率重建
2016-11-08叶坤涛郭振龙贺文熙
叶坤涛 郭振龙 贺文熙
(江西理工大学理学院 江西 赣州 341000)
基于Curvelet变换的压缩传感超分辨率重建
叶坤涛郭振龙贺文熙
(江西理工大学理学院江西 赣州 341000)
为了在无训练集的情况下,改善单帧退化图像的分辨率,实现了一种基于Curvelet变换和快速迭代收缩阈值法(FIST)的压缩传感超分辨率重建算法(Curvelet-FIST)。算法首先对低分辨率图像建立伪星形采样的采样方式,利用压缩传感理论,在Curvelet变换域,通过快速迭代收缩阈值法由采样值恢复出高分辨率图像。仿真实验表明,此超分辨率重建算法比传统的插值算法以及基于Wavelet变换和FIST的压缩传感重建算法(Wavelet-FIST)有更高的峰值信噪比。
压缩传感超分辨率Curvelet变换快速迭代阈值法星形采样
0 引 言
图像超分辨率重建,也称为图像放大,即通过一幅低分辨率图像或图像序列恢复出高分辨率图像的技术。它目前在医学成像、视频监控、遥感、高清电视等领域广泛应用。单帧图像的超分辨率重建大致可分为有训练样本集的基于学习的超分辨率重建和无训练样本集的图像增强超分辨率重建[1]。有训练样本集的超分辨率重建是从大量的训练样本集中获取先验知识作为超分辨率的依据,然后重建高分辨率图像。该类方法重建效果较好,但对所设定的训练样本集有依赖[2]。无训练样本集的图像增强是通过建立图像的物理退化模型,假定低分辨率图像是通过原始高分辨率图像经过几何变形、模糊和降采样得到的结果,利用算法反演高分辨率图像,该类方法操作简单,易于实现,例如插值法。传统的插值法包括最邻近插值、双线性插值、立方插值等,算法复杂度低,但因为没有针对图像的边缘和纹理特征进行特殊处理,所以导致重建的图像出现不同程度的边缘模糊、锯齿或块效应等问题[3]。
2006年以来,Candes等提出的压缩传感理论经常被应用到单帧图像的超分辨率重建领域。其中有压缩传感理论应用于无训练样本集的情况,如2006年,Sen等人在测量前引入高斯低通滤波过程,使得传感矩阵满足等距约束性RIP条件,然后利用正则化正交匹配追踪算法ROMP实现图像在小波域的压缩传感超分辨率重建[4];也有将该理论应用于有训练样本集的情况,例如2015年,Sun等人先对低分辨率图像双边滤波,然后通过对训练样本集实行K奇异值分解K-SVD算法,得到冗余字典并对图像稀疏表示,最后实现压缩传感超分辨率重建[5]。一般而言,无训练样本集的方法与有训练样本集的学习方法相比,具有不需要设定训练集、节省前期存储空间和数据运算量的优点。
压缩传感的实现与采用的恢复算法以及信号的具体稀疏方式有关[6]。同样,压缩传感理论应用到图像超分辨率重建时,恢复算法、稀疏方式也会影响超分辨率重建质量。
贪婪恢复算法一般都会面临产生巨大稀疏矩阵和测量矩阵的问题,对计算内存配置要求高,而凸优化算法中的迭代收缩阈值算法IST[7,8]可以避免生成维数很大的稀疏矩阵和测量矩阵。
常见稀疏方式有Wavelet和离散余弦(DCT),但它们缺点明显。DCT的时频分析性能不佳,Wavelet方向选择性差,不能很好地表示图像边缘的信息。而曲波(Curvelet)变换,融合了Wavelet变换的多尺度和脊波变换的各向异性特点,在细尺度下能更优地逼近曲线或直线,对图像的边缘细节和曲线等特征有更好的描述[9,10]。2014年,叶慧等实现了基于Curvelet变换的压缩传感[11],但并没有实现此框架下的图像超分辨率重建。
压缩传感理论应用到图像超分辨率重建的重要障碍是采样测量方法的建立。因为超分辨率重建要求的采样测量方法和压缩传感要求的采样随机性不同。
本文建立了对低分辨率图像的伪星形采样方法,并在Curvelet变换域,采用快速迭代收缩阈值算法FIST[7,12]恢复出高分辨率的图像,即实现了一种基于Curvelet变换和FIST的压缩传感(Curvelet-FIST)超分辨率重建算法。实验表明,与传统插值算法、基于Wavelet变换和FIST的压缩传感超分辨率重建算法(Wavelet-FIST)相比,具有更好的超分辨率重建效果。
1 稀疏方式与恢复算法
1.1压缩传感理论
在压缩传感理论中,设某个可稀疏化的长度为N的信号X的稀疏度为K,压缩传感的采样压缩过程可描述为:
y=ΦX=ΦΨα=Θα
(1)
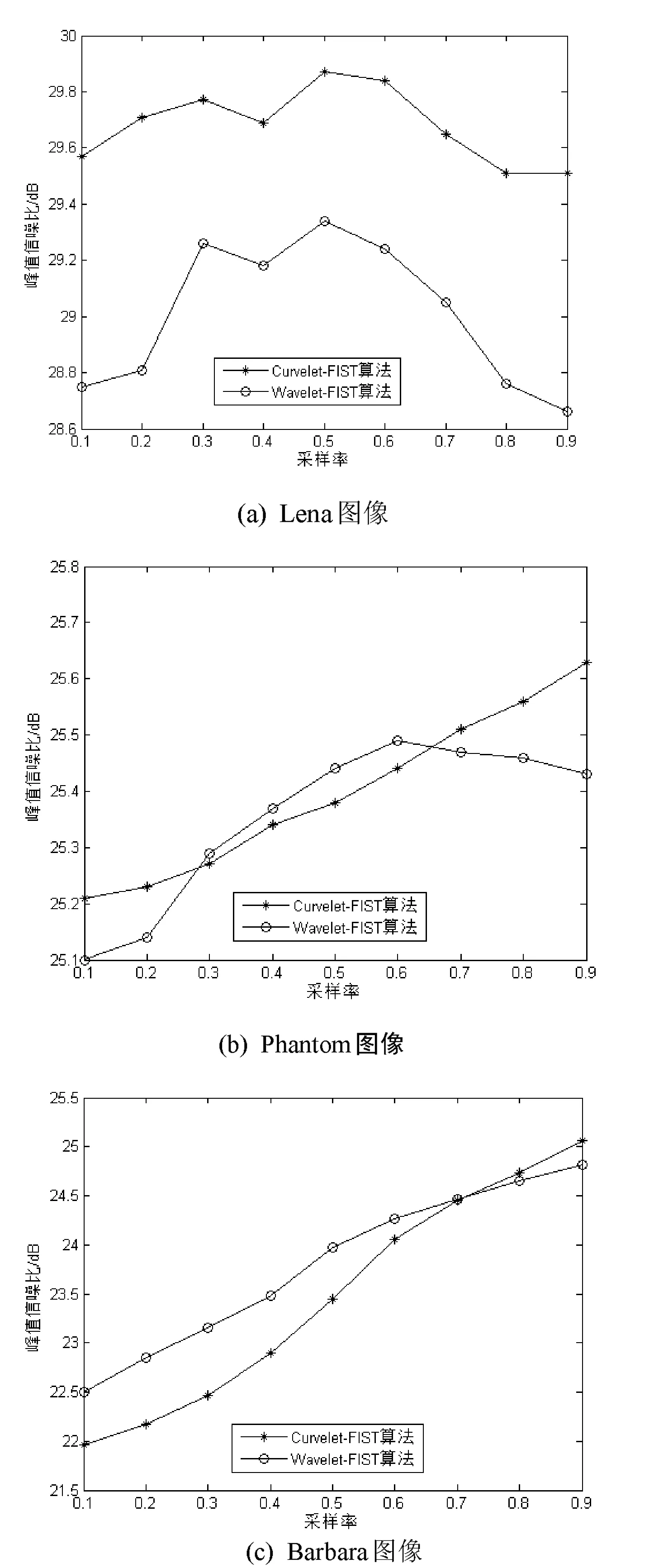
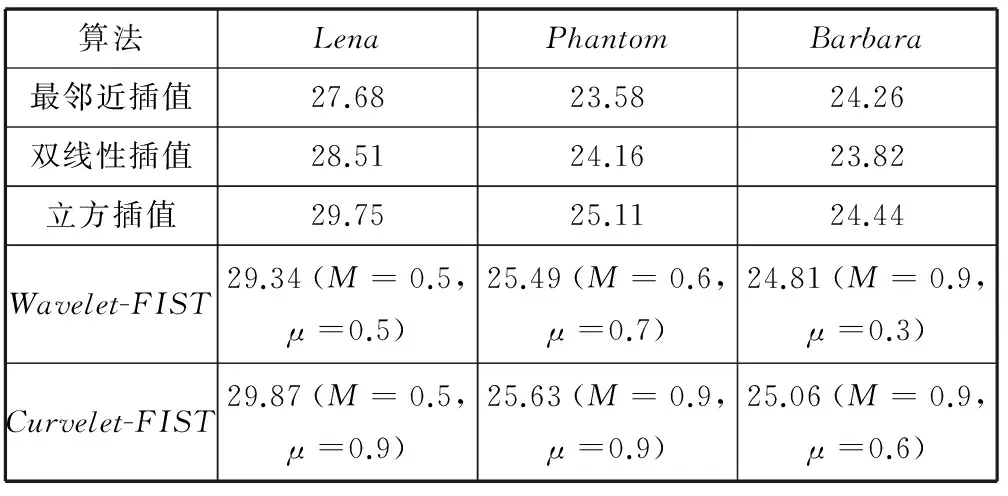
其中,Ψ与Φ分别是稀疏矩阵、测量矩阵;Θ=ΦΨ称为传感矩阵;y是长度为M(M (2) (3) 这是一个典型的凸优化问题,可以将其转化为一个线性规划问题求解。构造优化目标函数f(x),如式(4)所示: (4) (5) 式(5)构成了一个通过y、Φ和Ψ恢复出X的压缩传感数学模型。由该模型可知恢复出的X的质量好坏取决于测量矩阵Φ、代表稀疏方式的稀疏矩阵Ψ和恢复算法三个重要因素。 实际上,稀疏矩阵、测量矩阵分别抽象表示信号X的稀疏方式和采样测量方式,而精确重建信号X的具体方法即是恢复算法。 1.2稀疏方式 因为Curvelet变换是在单尺度脊波变换或局部脊波变换的基础上构造的,综合了脊波擅长表示直线特征和Wavelet适于表现点状特征的优点,能够克服DCT的时频分析性能不佳、Wavelet的方向选择性差的缺点,所以本文用Curvelet变换来实现图像的稀疏。 另外,实现第二代Curvelet变换的两种快速离散算法分别是基于不均匀采样的快速傅里叶变换USFFT(UnequisedFFT)和基于特殊选择的傅里叶采样的绕叠[15]。两种算法都是先通过FFT变换到频域,再在频域中进行局部化,然后对局部化后的结果做二维FFT逆变换,得到离散Curvelet变换系数;区别在于不同尺度和方向下空间网格的选择方法不同。由于USFFT算法比Wrapping算法计算量更大、速度更慢,因此,本文的Curvelet变换用Wrapping算法实现。 1.3恢复算法 求解式(5)的恢复算法主要包括最优化算法和贪婪算法。常用的最优化算法有凸优化算法、非凸优化算法及光滑l0范数算法等[16]。常用的贪婪算法有正交匹配追踪算法(OMP)、正则化正交匹配追踪算法ROMP、压缩采样匹配追踪算法(CoSaMP)等[17]。 Curvelet是一个多尺度几何变换,变换后的系数数据量大,用贪婪算法重建经常产生维数很大的稀疏矩阵和测量矩阵,对计算内存配置要求高,采用快速迭代收缩阈值算法可解决此问题。 迭代收缩阈值法的核心是对前一次的估计值进行阈值收缩处理从而来获得新的估计值[7,8]: (6) (7) Sc(X)具体实现步骤描述如下: 1) 在Ψ域中对X进行变换,得到变换系数α; 2) 确定阈值,对α软阈值处理,即执行阈值σ>0定义的软收缩函数Tσ(α): (8) 3) 对软阈值处理后的α进行Ψ域的逆变换,得到更新值X。 而FIST算法主要改进了Sc(X)函数,在原Sc(X)的实现步骤2)之前结合前两次的迭代系数值αk、αk+1,并引入参数t,对α进行更新,然后对更新后的α继续实现步骤2)、步骤3)。更新方法描述如下[7,12]: (9) 其中参数t的更新方法为: 基于Curvelet变换和IST法的压缩传感方法还未见用于图像的超分辨率重建,为了提高收敛速度本文用FIST算法代替IST算法,实现Curvelet-FIST算法,并通过设计采样方式测量矩阵,将此方法应用于图像的超分辨率重建。 应用sbar交班模式前,所检查的501例交班患者中存在交班缺陷者81例,缺陷率为16.17%,实施后所检查的504例交班患者中存在交班缺陷者19例,缺陷率为3.76%,两组间缺陷率对比组间比较差异存在统计学意义,X2=43.0999,P<0.05。 2.1超分辨率的采样测量方式 普通的图像压缩传感重建是将空域内的图像在某个变换域中稀疏表示,利用一个与变换基不相关的测量矩阵对稀疏图像随机测量,这样同时完成数据的采样和压缩两个过程,然后通过求解最优化问题可由少量的稀疏投影高概率的重建出原始图像。常见的采样测量矩阵在时域有高斯随机矩阵、局部傅里叶矩阵、置乱哈达玛矩阵等,也可以在图像的二维傅里叶变换域生成随机采样矩阵。Wan等在文献[18]中给出了傅里叶变换域的三种随机采样方法,它们分别是星形采样、双星形采样和星环采样[18]。星形采样过程先将图像的二维傅里叶变换系数中的低频信息移动到频谱图中心,然后与星形采样矩阵相乘来完成采样。星形采样矩阵的元素由0和1组成,如图1(a)所示。图1(a)为一个维数256×256,采样率M=0.3的星形采样矩阵实例,其中黑色位置为0,白色位置为1,显然白色射线条表示用于构造压缩测量值的频率位置,射线条数决定采样率M。 普通压缩传感中的采样测量方式必须做适当修正,才能用于单帧图像的超分辨率重建。首先由低分辨率图像按照新的采样方法构造出高分辨率图像的测量采样信号y,然后将高分辨率图像视为原信号X,通过压缩传感过程由测量值y恢复出原信号X。新的采样测量方法由星形采样改进而成,称为伪星形采样。伪星形采样的具体实现过程描述如下: (1) 经过立方插值将低分辨率图像XL放大一定倍数变成高分辨率估计图像XH; (2) 对XH进行二维快速傅里叶变换(FFT2),并重排傅里叶系数,把低频信息移动到频谱图中心; (3) 对XL进行FFT2,并重排傅里叶系数,把低频信息移动到频谱图中心; (4) 将步骤(2)中的频谱图中心,维数与XL相同的区域,用步骤(3)中的低频频谱图取代,得到XHN; (5) 按照XHN的维数建立星形采样矩阵; (6) 将星形采样矩阵的中心,维数与XL相同区域置为1,构造出新的采样矩阵,称为伪星形采样矩阵;图1(b)为在图1(a)基础上构造的伪星形采样矩阵,中间白色矩形部分的维数为128×128; (8) 对上述(7)的处理结果逆重排后,进行逆快速傅里叶变换得到高分辨率图像的测量值y。 图1 星形采样矩阵和与之对应的伪星形采样矩阵 这个新的采样测量方法,保留了低分辨率图像完整频率信息作为高分辨率图像的低频信息,同时也合理估计了高频信息,使重建出的高分辨率图像更符合视觉要求。实验发现,不同采样率的星形采样矩阵的重建效果也有所不同。 2.2Curvelet-FIST超分辨率算法 将基于Curvelet-FIST算法的压缩传感中的测量采样方法,修正为伪星形采样,得到基于Curvelet-FIST算法的图像超分辨率重建算法,其具体实现步骤详述如下: 1) 初始化:设定迭代停止参数ε,迭代步长γ,阈值σ=max_e×η(max_e是对低分辨率图像立方插值后图像的Curvelet变换系数的最大值,稀疏化阈值η>0),收缩因子μ(0<μ<1),迭代次数k=0。 2) 本文Curvelet-FIST算法的压缩传感的图像超分辨率重建: (1) 采用伪星形采样方法对低分辨率图像测量得到y,初始化Xk=y; (2) 对测量图像Xk进行Curvelet变换αk=ΨXk; (3) 计算残差Residual=αk-αk-1; (4) 迭代更新:αk+1=αk+γ×Residual; (5) 利用FIST方法更新tk+1与αk+1; (6) 软阈值处理:αk+1=Tσ(αk+1); (7)Curvelet逆变换:Xk+1=ΨTαk+1; (8) 软阈值松弛:σ=σ×μ; 3) 迭代重建过程停止判断条件:当σ<ε时,则停止迭代;否则,重复步骤2),直到满足阈值条件,输出Xk+1,得到重建的超分辨图像。 将前述基于Curvelet-FIST算法的图像超分辨率重建算法步骤中的Curvelet变换替换成Wavelet变换,还可实现基于Wavelet变换和FIST的压缩传感重建算法Wavelet-FIST。 实验平台搭建在内存为32GB的台式机上,使用工具及版本为Matlab2014a。为了客观描述超分辨率算法的优劣,首先用邻域平均插值法[19]从256×256的Lena、Barbara标准图像和Phantom医学高分辨率图像获得对应的128×128的低分辨率图像,然后分别采用最邻近插值、双线性插值、立方插值、Wavelet-FIST(sym8小波)、Curvelet-FIST算法对128×128的低分辨率图像进行256×256的超分辨率重建,并计算重建后图像与原256×256图像的峰值信噪比(PSNR),PSNR越大代表重建效果越好。 对每幅图像的Wavelet-FIST、Curvelet-FIST算法分别仿真81次。各次实验的参数在固定ε=10-3,γ=1.0,η=1.0的前提下,对介于0.1至0.9间隔0.1的每个M值,改变μ(从0.1开始以间隔0.1变化到0.9),并记录与每个M值对应的最大PSNR,如图2所示,图中的横坐标为M,纵坐标是与M对应的最大PSNR。在图2中可以明显看出,对Lena图像,Curvelet显然在不同的M值上,都比Wavelet的重建效果好;而对Phantom图像,在低M值和高M值的两端,Curvelet取得比Wavelet更好的重建效果;而对于Barbara图像,只在高M值的一端,Curvelet取得比Wavelet更好的重建效果。这是因为Curvelet变换的高度各向异性的特点,具有很强的表示图像中“沿”边缘信息的能力。Lena图像包含的光滑和边缘信息较多,适合Curvelet稀疏表示;Phantom图像显然在低M值和高M值的采样时,光滑边缘信息比重多,导致Curvelet稀疏效果好;而对于纹理信息丰富的Barbara图像,光滑边缘信息随M值增加,Curvelet变换的优点在高M值时才得以体现。 图2 不同图像的Wavelet-FIST、Curvelet-FIST算法效果对比图 虽然对于不同图像,不同M值,Curvelet-FIST与Wavelet-FIST相比重建效果不同,但是无论针对边缘信息比较多的Lena图像还是纹理信息比较多的Barbara图像和医学Phantom图像,Curevlet-FIST的81次超分辨率重建实验中的PSNR的最优值总是比Wavelet-FIST的高,而且Curvelet-FIST的超分辨率重建效果又都比传统的插值算法好,如表1所示。 表1 不同算法的峰值信噪比对照 表1记录了针对三幅图像,用传统插值算法超分辨率重建的PSNR以及Wavelet-FIST和Curvelet-FIST的超分辨率重建的PSNR最优值;括号中是算法最优值对应的μ和M取值。对Lena图像,Curvelet-FIST算法超分辨率重建的最优PSNR比最邻近插值、双线性插值、立方插值、Wavelet-FIST最优值依次提高了2.19、1.36、0.12、0.53dB;对Phantom图像,分别提高2.05、1.47、0.52、0.14dB;对Barbara图像,分别提高0.8、1.24、0.62、0.25dB。 为了使超分辨重建结果可视化,以Lena图像为例,除整体效果图外,选择细节信息特征较丰富的帽沿和肩部进行比较。实验结果如图3所示,每幅图中的左下角与右上角分别是帽沿和肩部的局部放大图。 图3 Lena图像效果图 在图3中,从整体上看,采用双线性插值方法使得图像整体较暗;从细节方面看,最邻近插值产生的锯齿现象十分明显,双线性插值图像虽然锯齿现象得到改善,但图像在细节处比较模糊。Wavelet-FIST算法虽然在细节处得到了很好的改善,但是边缘处不够平滑,Curvelet-FIST算法的重建图像在帽沿边缘和纹理细节等处更加平滑和清晰。 本文实现了一种基于Curvelet变换和快速迭代收缩阈值法的压缩传感超分辨率重建算法Curvelet-FIST,其核心思想是通过改进的星形采样,从低分辨率图像直接构造出高分辨率图像的采样值,然后按照压缩传感理论,将采样值在Curvelet变换域通过快速迭代阈值法重建出高分辨率图像。仿真实验结果表明,Curvelet-FIST对不同信息(光滑、纹理等)图像的超分辨率重建的效果,比传统插值及Wavelet-FIST算法均有提高。这一方面体现出压缩传感超分辨率重建与插值算法相比的优点,另一方面也体现出Curvelet变换与Wavelet变换相比在图像表示方面的优势。不足之处是该算法针对信息分布不同特点的图像,需要调整算法参数才能得到最理想的重建效果。以后的研究方向可从解决这个问题入手。 [1] 苏衡,周杰,张志浩.超分辨率图像重建方法综述[J].自动化学报,2013,39(8):1202-1213. [2]TaiYW,LiuS,BrownMS,etal.Superresolutionusingedgepriorandsingleimagedetailsynthesis[C]//Proceedingsof2010IEEEConferenceonComputerVisionandPatternRecognition(CVPR2010),SanFrancisco,USA,2010:2400-2407. [3] 樊博,杨晓梅,胡学姝.基于压缩感知的超分辨率图像重建[J].计算机应用,2013,33(2):480-483. [4]SenP,DarabiS.Compressiveimagesuper-resolution[C]//ConferenceRecordofthe43rdAsilomarConferenceonSignalsSystemsandComputers,California,USA,2009:1235-1242. [5]SunY,GuG,SuiX,etal.Singleimagesuper-resolutionusingcompressivesensingwitharedundantdictionary[J].IEEEPhotonicsJournal,2015,7(2):1-11. [6]BaraniukRG.Compressivesensing[J].IEEESignalProcessingMagezine,2007,24(4):118-121. [7]BeckA,TeboulleM.Afastiterativeshrinkage-thresholdingalgorithmforlinearinverseproblems[J].SiamJournalonImagingSciences,2009,2(1):183-202. [8] 焦淑红,唐琳,齐欢,等.迭代收缩阈值雷达前视成像方法[J].航空学报,2014,35(12):3384-3391. [9]CandesEJ,DonohoDL.Curvelets-asurprisinglyeffectivenonadaptiverepresentationforobjectswithedges[C]//CurvesandSurfaceFitting,Saint-Malo,France,1999:105-120. [10] 文奴,杨世植,崔生成.基于Curvelet-Wavelet变换高分辨率遥感图像降噪[J].浙江大学学报:工学版,2015,49(1):79-86. [11] 叶慧,孔繁锵.基于Curvelet变换的图像压缩感知重构[J].计算机工程,2014,40(2):233-236. [12]WangS,HuangTZ,LiuJ,etal.Analternatingiterativealgorithmforimagedeblurringanddenoisingproblems[J].CommunicationsinNonlinearScience&NumericalSimulation,2014,19(3):617-626. [13]CandesEJ,RombergJ,TaoT.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509. [14]DonohoDL,EladM,TemlyakovVN.Stablerecoveryofsparseovercompleterepresentationsinthepresenceofnoise[J].IEEETransactionsonInformationTheory,2006,52(1):6-18. [15]CandesEJ,DemanetL,DonohoD,etal.Fastdiscretecurvelettransforms[J].SiamJournalonMultiscaleModeling&Simulation,2005,5(3):861-899. [16] 练秋生,王艳.基于双树小波通用隐马尔可夫树模型的图像压缩感知[J].电子与信息学报,2010,32(10):2301-2306. [17]ZhangL.VideocodingbasedoncompressivesensingviaCoSaMP[J].JournalofDonghuaUniversity:englishEdition,2014,31(5):727-730. [18]WanT,CanagarajahN,AchimA.Compressiveimagefusion[C]//Proceedingsof15thIEEEInternationalConferenceonImageProcessing(ICIP2008),SanDiego,USA,2008:1308-1311. [19] 张莎,田逢春,谭洪涛.基于下采样的快速块匹配搜索算法及降噪应用[J].计算机应用,2010,30(10):2819-2822. COMPRESSEDSENSINGSUPER-RESOLUTIONRECONSTRUCTIONBASEDONCURVELETTRANSFORM YeKuntaoGuoZhenlongHeWenxi (CollegeofScience,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China) Inordertoimprovetheresolutionofsingle-framedegradedimagesundertheconditionofnoanytrainingset,weimplementedacompressedsensingsuper-resolutionreconstructionalgorithm,calledCurvelet-FIST,whichisbasedonCurvelettransformandfastiterativethreshold-shrinkage(FIST)algorithm.First,thealgorithmsetsupasamplingmodeofpseudo-star-shapesamplingonlow-resolutionimages.Thenbymakinguseofthetheoryofcompressedsensing,andinCurvelettransformdomain,itrestoresthehigh-resolutionimagefromsamplingvaluesthroughFISTalgorithm.Simulationexperimentshowedthatthissuper-resolutionreconstructionalgorithm,comparedwithtraditionalinterpolationalgorithmandthecompressedsensingreconstructionalgorithmbasedonWavelettransformandFIST(Wavelet-FIST),hashigherpeaksignal-to-noiseratio(PSNR). CompressedsensingSuper-resolutionCurvelettransformFastiterativethreshold-shrinkageStar-shapesampling 2015-09-02。国家自然科学基金项目(61368004);国家高层次留学人才回国资助项目([2011]481)。叶坤涛,博士,主研领域:MEMS,光谱测量与仪器。郭振龙,硕士生。贺文熙,硕士。 TP ADOI:10.3969/j.issn.1000-386x.2016.10.013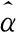
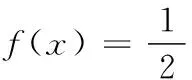
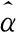
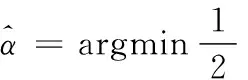
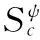
2 超分辨率重建实现

3 实验结果与分析

4 结 语
