基于三维构造张量的位场边界识别滤波器

周帅， 黄大年， 焦健

吉林大学地球探测科学与技术学院， 长春　130026



基于三维构造张量的位场边界识别滤波器

周帅， 黄大年*， 焦健

吉林大学地球探测科学与技术学院， 长春130026

地质体构造边界位置的确定是位场数据解释中的一项重要工作，现有很多基于位场梯度张量数据的边界检测滤波器，但存在识别边界位置模糊且无法均衡深浅地质体异常的缺点.本文定义了位场数据的三维构造张量，并提出基于位场构造张量的边界滤波器.为了同时显示不同振幅异常的边界位置，对新定义的滤波器进行归一化处理.在高阶均衡滤波器的计算中需要计算位场的垂向高阶导数，本文引入一种计算的稳定算法，基于拉普拉斯方程利用位场水平导数求解垂向导数，可减小垂向导数计算中产生的误差.将定义的滤波器应用到合成的重磁数据中证明了新方法相比传统的滤波器能更加清晰、准确地圈定边界位置，而且针对同时含有正负异常的地质情况，可避免产生额外的错误边界.最后将新的滤波器应用到实测的重磁数据的解释中，结果显示基于构造张量的滤波器可更准确清晰地划分出断裂的边界位置，发现更多的构造细节.

构造张量； 边界识别； 位场

1　引言

位场数据的边界检测是地球物理勘探中广泛应用的方法，它可以圈定地质体的水平位置，指导下一步的解释工作.目前，有很多方法用于地质构造边界的检测和拾取中.Cordell(1979)利用总水平导数的最大值圈定地质体的边界.Hood 和Teskey(1989)发现位场垂向导数的零等值线与地质体的边界相对应.Nabighian(1972)提出构造边界的位置可用解析信号振幅的最大值描述，后来，Hsu等(1996)利用高阶解析信号圈定的磁性体的边界位置更加清晰，提高了分辨率.但是上述方法均无法同时清晰地识别深部和浅部的重磁异常体的边界.为了解决这一问题，人们开始致力于均衡边界滤波器的研究，主要通过导数间的比值实现.Wang等(2010)分析了简单规则形体重力异常垂向导数零值位置的空间变化规律，垂向导数可圈定地质体的边界位置，且可用于均衡强弱振幅地质体异常.Cooper和Cowan(2006)、马国庆等(2012)利用垂向导数定义均衡滤波器，极大值位置对应地质体边界位置.Miller和Singh(1994)利用位场总水平导数与垂向导数的比值定义了均衡边界识别滤波器倾斜角(tilt angle).Verduzco和Fairhead(2004)计算倾斜角滤波器的总水平导数，并定义了新的高阶边界识别方法Thdr.Wijns等(2005)利用解析信号振幅均衡总水平导数，定义了新的滤波器Theta图，它的最大值位置可有效的同时圈定深浅地质体的边界位置.王万银等(2010)对位场边界识别的方法进行综述，指出位场倾斜角法和Theta图法边界检测结果与垂向一阶导数结果一致，且存在“解析奇点”的缺点.Ma(2013)利用不同阶导数的比值定义了新的边界识别器，使得圈定的边界位置更加清晰.Zhou等(2013)基于重力梯度张量矩阵的特征值定义了新的边界识别器，解决了含正负重力异常的复杂地质条件的边界识别问题，避免产生错误的边界.

构造张量被广泛应用于图像处理与特征拾取中.Weickert(1999)提出构造张量可用于确定图像的边界和角点位置.三维构造张量可有效地描述视频中的局部运动细节，并被广泛应用于视频的剪切中(Wang and Ma, 2003).Jeong 等(2006)将构造张量应用到地球物理解释中，利用构造张量实现地震图像断层的识别.Sertcelik和Kafadar(2012)将高斯函数卷积二维构造张量的特征值应用于重力数据的边界识别中，但此方法无法均衡深浅地质体异常.Ma等(2015)利用构造张量的水平和垂直方向导数定义新的均衡滤波器，解决了无法识别深部异常的问题.Yuan等(2014)指出与高斯函数进行卷积而定义的基于构造张量的边界识别器会模糊圈定的边界位置，他们定义新的滤波器，可更清晰地显示地质体位置.

本文定义了基于三维构造张量的边界识别滤波器，可清晰准确地显示不同振幅大小的边界.而且针对同时含正负异常的复杂地质情况，本文方法可避免产生多余的干扰边界.

2　基于三维构造张量的滤波器

2.1三维构造张量(ST)

Sertcelik和Kafadar(2012)定义了含高斯函数的二维构造张量，其表达式为：

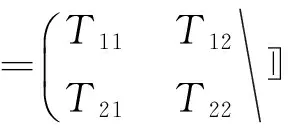
(1)

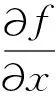
(2)

(3)

位场三维构造张量矩阵与位场梯度张量矩阵有相似的表达形式，现在有很多基于位场梯度张量的边界识别方法(Pedersen and Rasmussen，1990；Hansen and deRidder，2006；Beiki and Pedersen，2010；Beiki et al.，2012；Pilkington and Beiki，2013).本文对位场的构造张量进行分析，并定义了基于位场构造张量的边界识别滤波器.

2.2新提出的边界识别滤波器

我们利用位场构造张量(公式(3))的每一列定义表达式：

(4)

(5)

(6)

其中，STx和STy最大值位置分别描述地质体的N—S和E—W方向边界，STz极小值位置与地质体的边界位置对应，我们建立一棱柱体模型说明其效果.图1i所示为棱柱体产生的重力异常，虚线为棱柱体的水平位置，棱柱体顶部埋深1 km,厚度0.5 km，剩余密度100 kg·m-3.图1a—1b显示STx和STy可圈定出N—S和E—W方向的边界位置，STz的局部极小值位置描述出地质体的边界位置.利用STx和STy定义一种基于构造张量的边界滤波器：

(7)

SED的最大值对应地质体的边界，如图1g所示.对位场数据求垂向导数可提高分辨率(Hsu et al.，1996)，我们对公式(3)中的原始位场数据f求垂向一阶导数，并定义对应的边界滤波器：

(8)

(9)

(10)

图1　基于构造张量的边界滤波器效果(a) 异常的STx结果; (b) 异常的STy结果; (c) 异常的STz结果; (d) 异常的FSTx结果; (e) 异常的FSTy结果; (f) 异常的FSTz结果; (g) 异常的SED结果; (h) 异常的FSED结果; (i) 合成的重力异常.Fig.1　Results of edge detectors based on structural tensors(a) STx of anomaly; (b) STy of anomaly; (c) STz of anomaly; (d) FSTx of anomaly; (e) FSTy of anomaly; (f) FSTz of anomaly; (g) SED of anomaly; (h) FSED of anomaly; (i) Synthetic gravity anomaly.

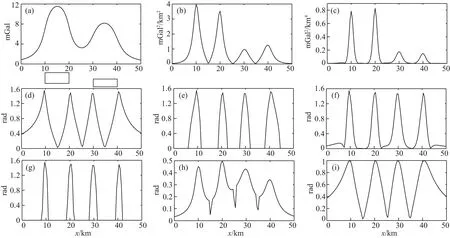
图2　不同方法边界识别结果的剖面图(a) 合成的重力异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果.Fig.2　Profiles showing edge detecting results using different methods(a) Synthetic gravity anomaly; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly.

图3　不同方法边界识别结果(a) 模型1合成的重力异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果.Fig.3　Edge detecting results using different methods(a) Synthetic gravity anomaly of model 1; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly.

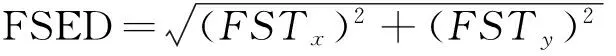
(11)

图1d—1f分别为FSTx、FSTy、FSTz边界识别效果，FSTx和FSTy相比低阶的STx和STy可更清楚地圈定出N—S和E—W方向的边界位置，对应的边界识别滤波器FSED(图1h)相比SED具有更高的边界识别分辨率.

2.3均衡的边界识别滤波器

建立如图2a所示的模型，埋深分别为1 km和2 km.图2b和2c分别为新提出的边界识别滤波器SED和FSED结果，利用垂向导数定义的滤波器FSED相比SED具有更高的分辨率，可更清晰地显示边界位置，但两种方法均存在无法均衡深浅模型异常的缺点.为了同时清晰地识别不同振幅的地质体异常，我们提出改进的基于位场构造张量的边界识别滤波器.STz的局部极小值与边界位置对应，我们采用STz对新定义的滤波器SED进行归一化处理，表达式为：

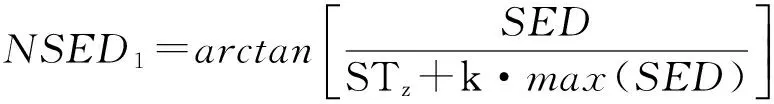
(12)

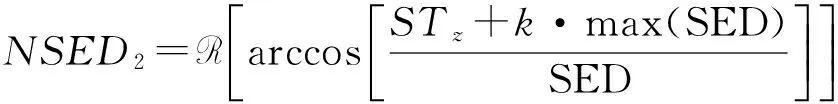
(13)

其中，R表示取实部运算；常数k用于避免在正负异常同时存在情况下产生额外错误的边界，取值一般为0到0.1，当只存在正异常或者负异常时，k取0，正负异常同时存在时，选择一定数值的k可消除假异常边界.k取值较大时会降低强弱振幅异常的均衡效果，对弱异常具有一定的压制作用，造成识别的弱异常边界位置不清晰；k取值较小时无法有效地消除在正负异常同时存在时带来的错误边界信息.实际计算中需要解释人员尝试不同的k值完成边界识别滤波器的计算，进而确定最优的边界识别结果.图2d和2e分别为NSED1和NSED2的边界识别结果，SED和FSED滤波器均可平衡深浅地质体异常.而且NSED2相比NSED1具有更高的分辨率，更清晰地显示边界位置.

边界识别滤波器FSED的均衡的边界滤波器表达式为：

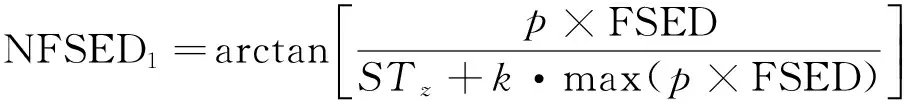
(14)

NFSED2=

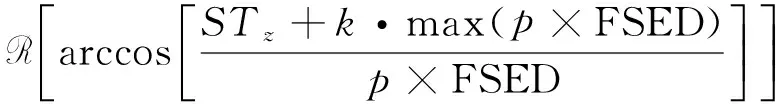
(15)

其中,

(16)

p用于平衡不同阶导数间的强度，使均衡的边界滤波器满足数学运算法则.为了说明本文方法的有效性，选择常用的倾斜角总水平导数Thdr和Theta图方法进行效果对比.Verduzco和Fairhead(2004)定义了倾斜角的总水平导数，表达式为：

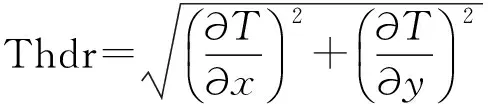
(17)

其中，

(18)

Wijns等(2005)利用解析信号的振幅均衡总水平导数，定义了均衡的边界滤波器Theta图：

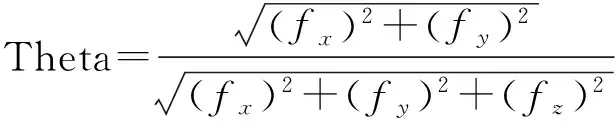
(19)

其中，f表示原始位场异常.图2h和2i分别为Thdr和Theta图滤波器边界识别效果，图2f—2g表明NFSED1和NFSED2最大值显示模型体的边界.相比传统的边界识别器，新定义的方法具有更高的水平分辨率.

在均衡边界识别器的计算中，需要计算位场f的高阶导数，频率域内的导数计算会放大噪声的干扰.为了减小噪声干扰，f的各阶水平导数在空间域采用有限差分的方式计算，而各阶垂向导数采用下列变换进行计算：

(20)

(21)

(22)

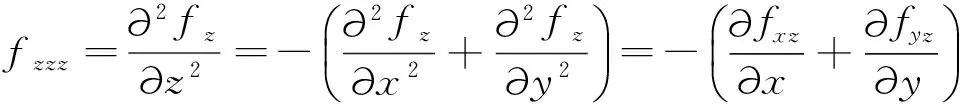
(23)

其中，fz的计算分两步进行，首先通过频率域内积分计算得到原始重磁异常f 的标量位U，进而利用空间域方法得到位U的二阶水平导数Uxx和Uyy，然后利用拉普拉斯方程求得fz(FediandFlorio,2002).频率域内积分和空间域水平导数计算不会放大噪声干扰，fz计算的表达式为：

(24)

3　理论模型试验

为了验证方法的有效性，建立如图3a所示的模型1，虚线标识地质体的真实水平位置，棱柱体1和3的顶面埋深为1km，棱柱体2和4的埋深为0.5km，剩余密度均为100kg·m-3.采用上述的方法对该模型重力异常进行处理，得到如图3b—3i的边界识别结果.SED和FSED滤波器可清晰地显示浅部棱柱体的边界位置，圈定的深部地质体边界位置模糊.传统的滤波器Theta图可均衡深浅异常，但是相比本文提出的均衡滤波器NSED1和NSED2，识别的边界位置比较发散.对比同阶导数的传统滤波器Thdr和NFSED1、NFSED2，传统的高阶导数滤波器Thdr识别的边界位置模糊，而本文新提出的方法可清晰准确地显示深浅异常，且NFSED2比NFSED1具有更高的边界识别分辨率.

位场实测数据中不可避免的含有噪声干扰，我们对模型2对应的重力异常中加入3%的高斯噪声.图5a为加入噪声后的重力异常，虚线为真实的地质体位置.图5h和5i所示传统滤波器Thdr和Theta图受噪声影响较大，无法显示棱柱体的边界位置.SED和FSED受噪声干扰影响较小，但无法均衡深浅地质体异常.利用高阶导数定义的滤波器NFSED1、NFSED2相比NSED1、NSED2放大了噪声干扰，但可更清晰地显示边界位置，具有一定的抗噪性.并且NFSED2相比同阶的NFSED1抗噪能力强，更加准确地圈定出地下不同埋深异常体的水平边界位置.在均衡滤波器计算中，因子k选择为0.01.

为了检验本文提出的均衡滤波器NSED1、NSED2、NFSED1、NFSED2在场源埋深差异较大情况下的边界识别效果，我们将图3a中的1和3号棱柱体的顶部埋深增大为2km，2和4号棱柱体顶部埋深仍为0.5km，剩余密度均为100kg·m-3，得到图6a—6d所示四个均衡滤波器的边界识别结果.改变1和3号棱柱体的剩余密度为-100kg·m-3，棱柱体其他参数不变，图6e—6h为对应的NSED1、NSED2、NFSED1、NFSED2边界识别效果.结果显示当深浅场源埋深四倍差别时，正负异常同时存在时可获得可靠的边界识别结果.继续增大1和3号棱柱体的顶部埋深为3km，剩余密度均为100kg·m-3，四个边界识别器在只存在正密度异常时可圈定出清晰的边界位置，可见图6i—6l.但是由于1和3号棱柱体埋藏较深，识别的边界位置与实际位置有一定的偏移.保持1和3号棱柱体的顶部埋深为3km，剩余密度改变为-100kg·m-3，图6m—6n显示NSED1和NSED2滤波器无法清晰地均衡深浅地质体异常.NFSED1和NFSED2识别的1和3号棱柱体的边界位置间断，如图6o和6p所示.当场源埋深差异较大时，针对只存在正异常或负异常的地质情况，均衡滤波器可获得清晰的场源边界位置，但圈定的边界位置与真实位置有一定偏差.对于正负异常同时存在的地质情况，新提出的边界识别器在六倍场源埋深差异时，圈定的边界位置出现间断，场源之间的空间位置临近关系也影响滤波器的边界识别结果.

图4　不同方法边界识别结果(a) 模型2合成的重力异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果.Fig.4　Edge detecting results using different methods(a) Synthetic gravity anomaly of model 2; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly.

图5　不同方法边界识别结果(a) 模型2加入3%高斯噪声合成的重力异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果.Fig.5　Edge detecting results using different methods(a) Synthetic gravity anomaly of model 2 with added 3% Gaussian noise; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly.

图6　不同场源埋深均衡滤波器边界识别结果埋深为2 km正异常时： (a)NSED1; (b) NSED2; (c) NFSED1; (d) NFSED2. 埋深为2 km负异常时：(e)NSED1; (f) NSED2; (g) NFSED1; (h) NFSED2. 埋深为3 km正异常时：(i)NSED1; (j) NSED2; (k) NFSED1; (l) NFSED2. 埋深为3 km负异常时：(m)NSED1; (n) NSED2; (o) NFSED1; (p) NFSED2.Fig.6　Edge detecting results using balanced filters with different source buried depthsPositive gravity anomaly with buried depth 2 km: (a) NSED1; (b) NSED2; (c) NFSED1; (d) NFSED2. Negative gravity anomaly with buried depth 2 km: (e) NSED1; (f) NSED2; (g) NFSED1; (h) NFSED2. Positive gravity anomaly with buried depth 3 km: (i) NSED1; (j) NSED2; (k) NFSED1; (l) NFSED2. Negative gravity anomaly with buried depth 3 km: (m) NSED1; (n) NSED2; (o) NFSED1; (p) NFSED2.

图7　吉林某地区重力异常边界识别结果(a) 实测重力异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果; (j) 异常的ETHD结果; (k) 异常的N_E结果; (l) 异常的N_HE图结果.Fig.7　Edge detecting results of gravity anomalies in an area of Jilin using different methods(a) Measured gravity anomaly; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly; (j) ETHD of anomaly; (k) N_E of anomaly; (l) N_HE of anomaly.

图8　朱日和地区化极磁异常边界识别结果(a) 化极后磁异常; (b) 异常的SED结果; (c) 异常的FSED结果; (d) 异常的NSED1结果; (e) 异常的NSED2结果; (f) 异常的NFSED1结果; (g) 异常的NFSED2结果; (h) 异常的Thdr结果; (i) 异常的Theta图结果; (j) 异常的ETHD结果; (k) 异常的N_E结果; (l) 异常的N_HE图结果.Fig.8　Edge detecting results of magnetic anomalies reduced to the pole in the Zhurihe area(a) Magnetic anomaly reduced to the pole; (b) SED of anomaly; (c) FSED of anomaly; (d) NSED1 of anomaly; (e) NSED2 of anomaly; (f) NFSED1 of anomaly; (g) NFSED2 of anomaly; (h) Thdr of anomaly; (i) Theta of anomaly; (j) ETHD of anomaly; (k) N_E of anomaly; (l) N_HE of anomaly.

4　实测数据应用

我们将本文所述方法应用到实测的重力和磁异常数据中验证方法的实际应用效果，对吉林某地区铁矿的剩余重力异常和朱日和地区的磁异常数据进行边界识别.图7a为吉林某地区的重力异常，采样间距0.1km，同时包含正负密度异常，该区主要以中心位置磁铁矿及黄铁矿化的矽卡岩引起的正异常为主，图中白线为根据前期工作划定的成矿带的大致范围.Zhou和Huang(2015)基于张量矩阵特征值定义了均衡的边界识别滤波器N_E和N_HE.王赛昕和刘林静(2011)提出了均值归一总水平导数边界识别方法ETHD，可同时显示深浅地质体异常的边界位置.我们引入N_E、N_HE和ETHD三种滤波器进一步对比分析本文方法的边界识别效果.从图7b—7l不同方法的边界识别结果可以看出，SED和FSED非均衡滤波器无法反映深部异常，识别的边界位置模糊.在计算均衡的滤波器NSED1和NSED2时，选择因子k等于0.0005，它们可同时显示深浅异常的边界位置，但分辨率差.高阶导数定义的NFSED1和NFSED2可清晰准确地圈定不同剩余密度的地质体构造边界，在计算中因子k选择为0.0005.传统滤波器Thdr识别效果差，无法清晰显示边界位置，Theta图可均衡深浅异常，但由于引入了额外的错误边界，造成边界相互连接，给解释带来了很大的误导.N_E和ETHD可稳定地圈定出异常体的边界位置，但相比本文提出的均衡滤波器，它们识别的边界位置模糊.当数据中含有一定噪声干扰时，高阶滤波器N_HE由于需要计算位场的垂向高阶导数，造成计算结果的不稳定.

由于磁异常受磁化方向的干扰，为了获得可靠的解释结果，在应用本文方法进行磁异常处理时，需要对原始磁异常进行化极处理.图8a为朱日和地区化极后的磁异常图，采样间隔为20m，测量区域为新元古代层序，主要由大陆沉积物构成，除一些含铁的沙堰堤坝外基本不含铁磁性物质.磁异常数据主要由堤坝产生的近线性异常和铁异常构成.本文提出的均衡的边界滤波器相比传统的滤波器Thdr和Theta图具有更高的分辨率，且可避免产生由正负异常存在时的错误边界.N_E、N_HE和ETHD可大致显示出构造的边界位置，但识别的边界位置不清晰.其中，利用公式(12)—(15)计算时，k选择为0.0001.

5　结论

本文定义了位场的构造张量矩阵，对矩阵进行分析并建立了新的边界识别滤波器.为了克服滤波器无法均衡深浅异常的缺点，对其进行归一化处理，定义了均衡的边界识别滤波器.在同时含有正负异常的复杂情况下，传统的滤波器会产生错误的干扰边界信息，通过引入因子k消除了这一干扰，但当场源埋深差别较大时会造成识别的深部场源边界间断.将基于位场构造张量的边界识别滤波器应用到合成的和实测的重磁异常中，新定义的均衡滤波器相比传统滤波器Thdr和Theta图在均衡深浅异常的同时，更清晰准确地圈定构造边界的水平位置，发现更多的小构造信息，更有利于指导下一步的勘探工作.

致谢感谢吉林大学地球探测科学与技术学院马国庆副教授提供的实测数据及在论文写作中给予的帮助.感谢审稿专家及编辑对本文提出的宝贵的修改意见.

Beiki M, Pedersen L B. 2010. Eigenvector analysis of gravity gradient tensor to locate geologic bodies.Geophysics, 75(6): 137-149.

Beiki M, Clark D A, Austin J R, et al. 2012. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data.Geophysics, 77(6): J23-J37. Cooper G R J, Cowan D R. 2006. Enhancing potential field data using filters based on the local phase.Computers&Geosciences, 32(10): 1585-1591. Cordell L. 1979. Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin, New Mexico∥Ingersoll R V ed. Guidebook to Santa Fe Country, 30th Field Conference. New Mexico Geological Society Guidebook. Virginia, USA: 59-64.Fedi M, Florio G. 2002. A stable downward continuation by using the ISVD method.GeophysicalJournalInternational, 151: 146-156. Hansen R O, deRidder E. 2006. Linear feature analysis for aeromagnetic data.Geophysics, 71(6): L61-L67. Hood P J, Teskey D J. 1989. Aeromagnetic gradiometer program of the geological survey of Canada.Geophysics, 54(8): 1012-1022. Hsu S H, Sibuet J C, Shyu C T. 1996. High-resolution detection of geologic boundaries from potential-field anomalies: An enhanced analytic signal technique.Geophysics, 61(2): 373-386.

Jeong W K, Whitaker R, Dobin M. 2006. Interactive 3D seismic fault detection on the Graphics Hardware.∥Proceedings of the 2006 International Workshop on Volume Graphics. Boston, USA: 111-118.

TCP采用网络服务器和客户端的方式进行通信。服务器主要负责发送数据至多个客户端或者从多个客户端读取数据，同样，客户端可以向所对应的服务器发送请求并获取所需数据。服务器与客户端传输是双向的，区别在于服务器可同时连接多个客户端。

Ma G Q, Huang D N, Yu P, et al. 2012. Application of improved balancing filters to edge identification of potential field data.ChineseJournalofGeophysics(in Chinese), 55(12): 4288-4295, doi: 10.6038/j.issn.0001-5733.2012.12.040.

Ma G Q. 2013. Edge detection of potential field data using improved local phase filter.ExplorationGeophysics, 44(1): 36-41.

Ma G Q, Liu C, Huang D N. 2015. The removal of additional edges in the edge detection of potential field data.JournalofAppliedGeophysics, 114: 168-173.

Miller H G, Singh V. 1994. Potential field tilt—a new concept for location of potential field sources.JournalofAppliedGeophysics, 32(2-3): 213-217. Nabighian M N. 1972. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: Its properties and use for automated anomaly interpretation.Geophysics, 37(3): 507-517.

Pedersen L B, Rasmussen T M. 1990. The gradient tensor of potential field anomalies: Some implications on data collection and data processing of maps.Geophysics, 55(12): 1558-1566.

Pilkington M, Beiki M. 2013. Mitigating remanent magnetization effects in magnetic data using the normalized source strength.Geophysics, 78(3): J25-J32.

Sertcelik I, Kafadar O. 2012. Application of edge detection to potential field data using eigenvalue analysis of structure tensor.JournalofAppliedGeophysics, 84: 86-94.

Verduzco B, Fairhead J D. 2004. New insights into magnetic interpretation using the 3-D analytic signal.TheLeadingEdge, 23(2): 116-119.

Wang H Y, Ma K K. 2003. Automatic video object segmentation via 3D structure tensor.∥Proceedings of 2003 International Conference on Image Processing. Barcelona, Spain: IEEE.

Wang S X, Liu L J. 2011. Edge detection by equalized and normalized amplitude of total horizontal derivatives.ChineseJournalofEngineeringGeophysics(in Chinese), 8(6): 699-704. Wang W Y, Zhang G C, Liang J S. 2010. Spatial variation law of vertical derivative zero points for potential field data.AppliedGeophysics, 7(3): 197-209.

Wang W Y, Qiu Z Y, Yang Y, et al. 2010. Some advances in the edge recognition of the potential field.ProgressinGeophysics(in Chinese), 25(1): 196-210, doi: 10.3969/j.issn.1004-2903.2010.01.027.

Weickert J. 1999. Coherence-enhancing diffusion of color images.ImageandVisionComputing, 17(3-4): 201-212.

Wijns C, Perez C, Kowalczyk P. 2005. Theta map: Edge detection in magnetic data.Geophysics, 70(4): L39-L43.

Yuan Y, Huang D N, Yu Q L, et al. 2014. Edge detection of potential field data with improved structure tensor methods.JournalofAppliedGeophysics, 108: 35-42. Zhou S, Huang D N. 2015. Edge detection using directional eigenvalues of potential field gradient tensor data.GlobalGeology, 18(3): 188-195. Zhou W N, Du X J, Li J Y. 2013. The limitation of curvature gravity gradient tensor for edge detection and a method for overcoming it.JournalofAppliedGeophysics, 98: 237-242.

附中文参考文献

马国庆, 黄大年, 于平等. 2012. 改进的均衡滤波器在位场数据边界识别中的应用. 地球物理学报, 55(12): 4288-4295, doi: 10.6038/j.issn.0001-5733.2012.12.040.

王赛昕, 刘林静. 2011. 均值归一总水平导数边界识别方法. 工程地球物理学报, 8(6): 699-704.

王万银, 邱之云, 杨永等. 2010. 位场边缘识别方法研究进展. 地球物理学进展, 25(1): 196-210, doi: 10.3969/j.issn.1004-2903.2010.01.027.

(本文编辑何燕)

A filter to detect edge of potential field data based on three-dimensional structural tensors

ZHOU Shuai, HUANG Da-Nian*， JIAO Jian

CollegeofGeoexplorationScienceandTechnology,JilinUniversity,Changchun130026,China

To detect the edge of potential field is an important task in identifying the horizontal position of geological structure. Although there are many methods based on potential field gradient tensors used to edge detection, the resolved edges remain blurred and inaccurate. This paper defines the structural tensors of a potential field and develops the related edge detectors to outline sources edges. In order to display different-amplitude anomalies simultaneously, we purpose two normalization strategies. When we calculate the new edge detectors, high-order vertical derivatives of potential field computation can increase the noise effect. The new calculation algorithm using horizontal derivatives to calculate vertical derivatives based on Laplace equation is applied to solve this problem. The presented filters tested on a synthetic potential field model show that they can outline the source edges clearly and accurately compared with traditional detectors. For complex situations with positive and negative anomalies, the new methods will not cause extra false edges. At last, we apply these new detectors to the real measured gravity and magnetic data. The results indicate that the new methods have ability to display edges of geological structures clearly and accurately and to discover more subtle information.KeywordsStructural tensor; Edge detection; Potential field

10.6038/cjg20161028.Zhou S, Huang D N， Jiao J. 2016. A filter to detect edge of potential field data based on three-dimensional structural tensors.ChineseJ.Geophys. (in Chinese),59(10):3847-3858,doi:10.6038/cjg20161028.

国家高技术研究发展计划(863计划)课题(2014AA06A613)资助.

周帅，男，1988年生，博士研究生，主要从事位场数据处理及解释方面的研究.E-mail:zhoushuai14@mails.jlu.edu.cn

黄大年，男，1958年生，教授，博士生导师，主要从事移动平台探测数据处理与解释及一体化软件平台开发.E-mail:dnhuang@jlu.edu.cn

10.6038/cjg20161028

P631

2015-12-13，2016-06-27收修定稿

周帅， 黄大年， 焦健. 2016. 基于三维构造张量的位场边界识别滤波器. 地球物理学报，59(10):3847-3858,