平衡力是洛伦兹变换下的不变量
2016-11-08李冬雪
李冬雪
湖北襄阳诸葛亮中学
平衡力是洛伦兹变换下的不变量
李冬雪
湖北襄阳诸葛亮中学
本文将证明平衡力是洛伦兹变换下的不变量,解决了非加速力在狭义相对论中的变换问题,并基于此提出了平衡力不变原理。
狭义相对论;平衡力;洛伦兹变换;S系;坐标变换;S’系
1 平衡力的变换问题
光速不变原理是从实验概括出来的,也是狭义相对论【1】基本假设之一。而长度、时间、速度都是洛伦兹变换下的协变量。一般认为,相对论力学中,力也是洛伦兹变换下的协变量。变换方程可由洛伦兹变换和力学定律推出。
由于牛顿力学方程F=dp⇀dt,力与时间相关,这引起力有一个变换式。设S及S’为惯性系,S’系相对S系速度为u沿X轴正向移动,在S系及S’系建立笛卡尔坐标,S(x,y,z)
S’(x’,y’,z’),S’中的X’轴与S中的X轴重合,S’在S中以速度u沿X轴正向移动。因此,力的变换为:

C为光速,物体在S’系速度。
当只有平衡力作用在物体上,物体会保持匀速直线运动状态或静止状态。因此F=dp⇀dt=0表示物体受合力为零,虽然如此,平衡力的存在可表现为使物体形状发生变化,而不是使动量p发生变化。若是物体为一弹簧,作用在其上一对平衡力大小F=kΔx,Δx为弹簧受力与不受力时的长度差,称为伸长量。
那么,平衡力否也遵循力的相对论变换呢?平衡力的合力为零,如果将平衡力的合力在不同惯性系变换,按相对论力的变换公式合力仍为零。那么,一对平衡力是否也单独遵循力的相对论变换呢?如果,平衡力单独遵循力的相对论变换,变换后再合成,其合力仍为零。这样认为的确是一种方便的作法,但也是不可靠的。因为,平衡力的合力为零,其效果(使物体发生形变)与时间没有关系,所以,平衡力是否单独变换不能够按通常的做法由力学定律及洛伦兹变换共同推出,只能由平衡力的效果,即使物体发生可测形变大小来推出。
而非平衡力的相对论变换与时间t有不可分割的关系,要遵循力的相对论变换式1—1。
2 平衡力不变原理
弹簧的伸长可测量力的大小,平衡力可以用弹簧的伸长测定。设计如图装置:物体A只能沿管m内运动,物体B只能沿管n运动。A物体和B物体之间存在斥力,m、n只可沿与其垂直方向,就是沿Y轴运动,有弹簧在其中间。设有惯性系S(x,y,z)S’(x’,y’,z’),轴X、X’与管m、n平行。
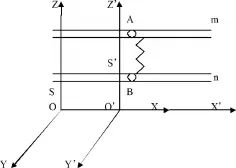
图 2—1
A物体受B物体Z正向斥力和m管给它的负Z方向的压力,B物体受A的负Z方向的斥力和管n给它的Z向的压力。当整个装置稳定不动时,A、B受平衡力,弹簧显示
(△x)A与B斥力的大小。
状态1:S’系相对S系静止,此时,S系有甲、乙两个测量员用相同的尺子测弹簧长度,他们测得值相同。
状态2:甲发现乙测量员与S’系、弹簧、两管m、n及物体A、B一起向右运动起来,稳定后,S’系相对于S系速度为V,S系与S’系都是惯性系,S’系沿X轴正方向运动。而在乙看来,甲同S系一起以—V速度沿X轴负方向运动。对乙来说,弹簧和A、B物体一直相对他静止。乙这时又测了一次弹簧长度,发现与前一次测得结果相同。甲这时发现乙的尺子竖直(沿Z’轴)和自己的尺子一样长,他对照乙的尺子将乙的测量结果标在自己的尺子上,而乙的测量结果在S’系与弹簧等长,甲实际上又测了一次弹簧长度。由于乙发现弹簧长度未变,所以甲也发现弹簧长度未变。两个系弹簧伸长也相同有△x=△x’
甲知道相对论的结果,当尺与速度方向平行时,会有洛伦兹收缩,但他们的尺子都与速度方向垂直,不会收缩,应当测到相同的值。
设△x是在S系弹簧伸长,△x’是在S’系弹簧伸长,就有△x=△x’
现在假设:“每个平衡力之一是单独遵循相对论力的变换的。设弹簧在S系受拉力Fz,在S’系受拉力Fz’
在状态1,S系与S’系相对静止。显然,Fz=Fz’由于Fz=k△x Fz’=k’△x’测得△x=△x’推出k=k’
在状态2,S’系相对S系以速度V运动,按平衡力单独遵循相对论力的变换的假设,有

由于Fz=k△x Fz’=k’△x’并且已经证明状态2有△x=△x’所以将Fz、Fz’代入(2)中会有k=由于γ0=(1->1所以k’>k而k’是静止弹簧的倔强系数,k是运动后的倔强系数,所以此结果说明“弹簧倔强系数由于运动变小了”。
这个结果对不对呢?让我们看另一种情况。
状态3:这时甲看到弹簧停止了运动,而乙与电荷仍以速度V向X轴正方向运动,同时乙看到弹簧与甲一起向X轴负方向以-V速度运动。
甲这时想到,弹簧停止了运动,不再是“倔强系数由于运动变小”,倔强系数比状态2变大了,而A、B物体间斥力不变,弹簧伸长量将变小,这时测得弹簧长度应比状态2小。
乙这时想到,弹簧运动了,它的“倔强系数由于运动变小”。而A、B物体间斥力不变,所以弹簧应伸得更长,弹簧长度应测得比状态2变大。
如果真的按他们的想法会测出不同的结果吗?我们知道,甲、乙两个测量员的尺子沿Z轴方向放置长度是相同的,根据前面的分析对同一根弹簧现在测得的值应该相同,由此测量与推断发生矛盾。
由于矛盾的存在,前述k=即“弹簧倔强系数由于运动变小了”肯定是错误的,这里我们认定k与k’的值与运动状态无关可使矛盾得以解决。又因为“弹簧倔强系数由于运动变小了”是“平衡力是单独遵循相对论力的变换”这一假设的直接结果。显然,“平衡力是单独遵循相对论力的变换”这一假设错误。我们还可以类似的证明除非认为在不同的惯性系之间平衡力Fz=Fz’,任何其他的变换都会引起矛盾的结果。
这里我们能得出的唯一结论是:“平衡力在不同惯性系中是大小不变的”,在我们讨论的情况下,弹簧伸长的方向,也就是力的方向,也是不变的。于是,我们得到了平衡力不变的原理。
应当指出前面的讨论,平衡力与弹簧运动方向垂直是较特殊的方向,普遍方向的平衡力不变原理这里就不再讨论,以上结果足够后面的讨论了。
[1]《相对论的意义》A.爱因斯坦著.李灏译.科学出版社1961,22-23
李冬雪(1972-),男,汉族,黑龙江省肇东人,中学一级职称,本科,湖北襄阳诸葛亮中学,研究方向:电磁学。
