一道几何竞赛题在圆锥曲线中的推广

张留杰　王小平

北京市陈经纶中学　(100020)



一道几何竞赛题在圆锥曲线中的推广

张留杰王小平

北京市陈经纶中学(100020)

图1

题目如图1，A为⊙O外一点，过点A作⊙O的割线l与⊙O交于点B，C，B′为点B关于OA的对称点．证明：OA与CB′的交点位置与直线l的选择无关．

这是第58届白俄罗斯数学奥林匹克竞赛的一道平面几何题，问题结构虽然简单，但是内涵十分丰富，尤其是将其推广到圆锥曲线，能充分揭示图中几何元素之间的内在联系，体现有心圆锥曲线的一类定值与定点问题．

将圆压缩为椭圆，可得

图2

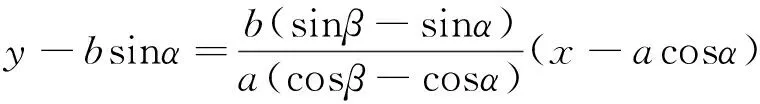
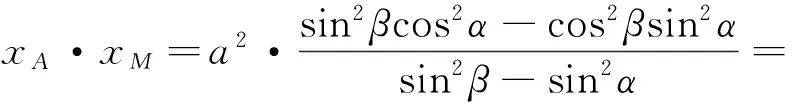
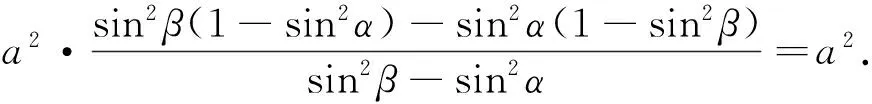
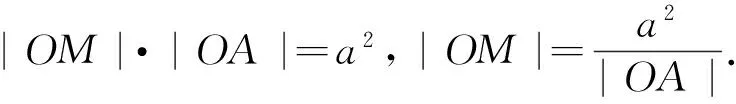
如果将椭圆改为双曲线，利用参数法，同理可证此结论也是正确的；如果点A在y轴上，可得|OM|·|OA|=b2，点M的位置依然和直线l的选择无关．

所以可得如下结论：

结论1已知中心在原点的有心圆锥曲线W，点A为曲线外x轴(y轴)上的一点，过A作曲线W的割线l，与曲线W交于点B、C，点B关于x轴(y轴)的对称点为B′，连结CB′与x轴(y轴)交于点M，则点M的位置与直线l的选择无关．

根据推广1，不难发现只要点A确定，点M就随之唯一确定，点M和点A的这种对应关系中是否蕴含其它几何特征呢？根据直线l的任意性，借助信息技术手段，我们发现当直线l运动为椭圆的切线时，点M恰好与过点A所引的两条切线的切点共线．

于是得出

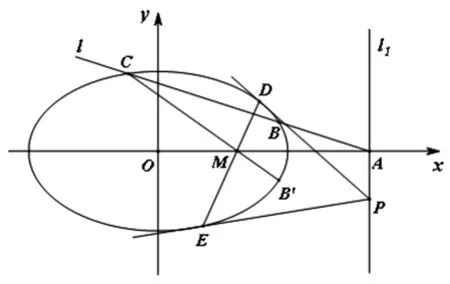
图3

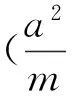
若将椭圆改为双曲线，同理可证此结论也是正确的．于是可得

结论2已知中心在原点的有心圆锥曲线W，点A为曲线外x轴(y轴)上的一点，过A作曲线W的割线l，与W交于点B、C，点B关于x轴(y轴)的对称点为B′，连结CB′与x轴(y轴)交于点M，过点A作直线l1⊥x轴(y轴)，点P为l1上的任意一点，过点P作曲线W的两条切线为PD，PE，切点分别为D，E，则点D，M，E三点共线．

通过压缩变换将圆中有关问题推广到椭圆中，然后再推广到双曲线中，得到更有价值和意义的新问题，是我们研究几何问题的一条途径，也是探究有心圆锥曲线性质的一种常用方法．