影响加筋土挡墙地震稳定性的参数分析
2016-11-07王恩喜孙树林陈怿旸
王恩喜,孙树林,2,陈怿旸,刘 俊,刘 博,李 方
(1.河海大学 地球科学与工程学院,江苏 南京 211100;2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;3.江苏省南京工程高等职业学校,江苏 南京 211135)
影响加筋土挡墙地震稳定性的参数分析
王恩喜1,孙树林1,2,陈怿旸1,刘 俊1,刘 博1,李 方3
(1.河海大学 地球科学与工程学院,江苏 南京 211100;2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;3.江苏省南京工程高等职业学校,江苏 南京 211135)
针对现有挡土墙抗震设计影响因素考虑不足等问题,运用拟静力法和水平条分法分析加筋土挡墙的地震稳定性,并研究土体内摩擦角、水平地震力加速度系数、填土粘聚力、挡土墙倾角和滑动体上部荷载等参数对地震稳定性的影响。结果表明:加筋土挡墙的地震稳定性与水平地震力加速度系数和滑动体上部荷载有显著关系,且变化趋势与之成正比;与土体内摩擦角和填土粘聚力的变化趋势成反比;当条件相同时,倾斜加筋土挡墙的地震稳定性比竖直挡墙的稳定性好。
加筋土挡墙;稳定性;参数;拟静力法;水平条分法
加筋土挡墙由于重量轻、施工简便和造价低廉等特点得到广泛应用。早期挡土墙设计多采用拟静力法[1-2];Shukla[3]改进了之前的理论,考虑土的粘聚力和内摩擦角对挡墙地震稳定性的影响;由于对加筋结构的分析存在明显的不足,Shahgholi[4]用水平条分法分析挡墙的内部稳定性,推导出筋材拉力公式;蒋建清等[5]提出地震作用下加筋土挡墙内部稳定性分析的水平条分方法;Ling等[6]考虑水平地震力和土壤特性的影响分析加筋土挡墙的稳定性;阮晓波等[7]运用拟静力-水平条分法,考虑多种因素对筋材拉力总和系数的影响;因拟静力法与实际地震波传播情况有较大差异,Nimbalkar等[8]用拟动力法分析加筋土挡墙曲面破裂面的边坡稳定性;程亚男等[9]基于拟动力-水平条分法,推导出筋材拉力和临界破裂角公式;汪益敏等[10]利用FLAC软件,研究了地震持续时间、地震波和地震峰值加速度对加筋土挡墙地震稳定性的影响。然而以前的研究,很少有涉及挡墙倾角和滑动体上部荷载对加筋土挡墙地震稳定性的研究,针对这一问题,本文在前人研究的基础上,运用拟静力-水平条分法,讨论影响加筋土挡墙的地震稳定性的主要参数。
1 分析方法
加筋土挡墙高H,刚性倾斜面与水平面的夹角β,如图1所示。假定挡墙后填土是均质的,每层筋材受水平拉力,选取各自变量为研究对象,设填土重度γ、内摩擦角φ、粘聚力c和填土表面均布荷载q。本文运用Shahgholi[4]改进的水平条分法,假定为多线性破裂面,滑动体被分为多个水平土条,不用考虑钢筋引起的条间力问题。
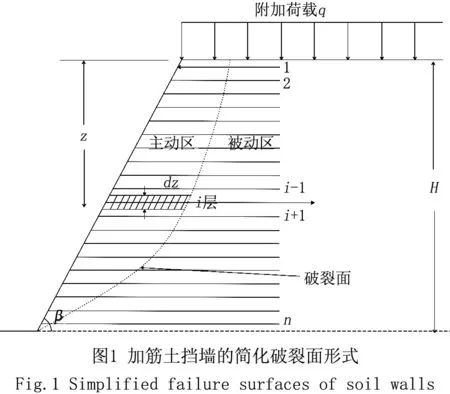

图2为第i个水平土条受力图,图中Wi为土体自重;Vi、Vi+1、Hi、Hi+1分别为水平土条上、下两侧的法向条间力和切向条间力;Ni和Si分别为滑动面的法向反力和切向反力;Ti为第i层钢筋所受拉力;Qhi为作用在土条上的水平地震惯性力;ai为第i个水平土条破裂面与水平面的夹角;β为挡土墙坡角。
基本假设如下:每一个土条的法向条间力等于土条上部的超载;破裂面通过挡墙的墙趾;滑动体安全系数Fs为破裂面上抗剪强度tf与剪切应力tr的比值,即;Fs=tf/tr;每个土条上的安全系数Fs均相等。
2 方程简化
挡墙后填土分为n个水平土条,则公式中有2n+1个未知数和2n+1个方程,未知数为n个法向反力、n个切向反力和1个筋材所需拉力;方程数为n个竖直方向的静力平衡方程、n个切向反力平衡方程和1个滑动体整体受力平衡方程。考虑多线性破坏面的情况,采用拟静力-水平条分法计算筋材所需拉力。墙后深度为z处水平土条受力如图2所示。第i个土条所受的重力:
(1)
每个土条包含一层钢筋,只考虑水平地震力作用在土条上,作用在第i个土条上的水平地震力可表示为:
Qhi=miah=Wikh
(2)
土条在竖直方向上力的平衡方程为:
Vi+1-Vi-Wi+Sisinai+Nicosai=0
(3)
式中,Vi和Vi+1为土条上、下条间法向力。
剪切应力为:
tr=tf/Fs
(4)
第i个破裂面上的切向反力为:
(5)
整个滑动体达到受力平衡时,滑动体上部荷载q产生的合力W,水平分量为0,即
(6)
将式(5)代入式(3)得:
(7)

当安全系数是已知时,筋材拉力总和是确定的,筋材拉力总和等效于土压力系数K[7]。
(8)
分析第i个土条,ai为土条破裂面与水平面的夹角,达到线性破坏时,此时筋材拉力最大。为满足上述情况,使筋材拉力总和最大化。整体为圆弧滑动面,如图1所示,筋材通过锚固于土中来保持内部稳定性,每个土层包含一个筋材,对土条受力分析见图2,筋材拉力Ti可以求出。
3 结果与讨论
抗剪强度指标(粘聚力和内摩擦角)、挡墙倾角、水平地震力加速度系数和附加荷载是影响加筋土挡墙地震稳定性的主要因素。研究上述参数对挡墙性能的影响,算例如下:加筋土挡墙高H=5m,安全系数Fs=1.0,填土重度γ=18kN/m3。考虑以下参数的变化:填土粘聚力c=0、5、10、15kPa,土体内摩擦角φ=20°、25°、30°、35°,水平地震力加速度系数kh=0.0、0.1、0.2,挡墙倾角β=75°、80°、85°、90°。墙后滑动体分为20个水平土条,筋材位于土条中间且等于水平土条数。与水平地震力相比,竖向地震力可忽略不计,故本文中没有考虑。
3.1土体内摩擦角
图3中c=0kPa,kh=0.2,β=90°。描述了φ和q对K的影响,K随q的增加而增大。q=0kPa,φ分别从20°增大到30°和35°时,K分别降低29.8%和41.5%;q=40kPa,φ分别从20°增大到30°和35°时,K分别降低30.3%和42.5%。这说明:不论回填土上部有无附加荷载,内摩擦角对加筋土挡土墙的地震稳定性影响几乎相同。

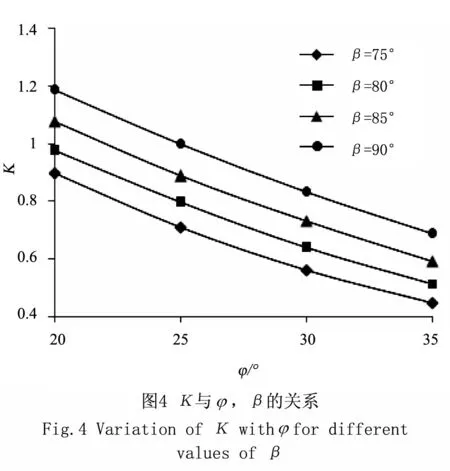
图4中c=0kPa,kh=0.2,q=40kPa。描述了φ和β对K的影响,K随φ的增加而增大。β=75°,φ分别从20°增大到30°和35°时,K分别降低37.4%和50.2%;β=90°,φ分别从20°增大到30°和35°时,K分别降低30.0%和42.0%。这说明:与竖直挡土墙相比,内摩擦角对倾斜挡土墙的影响更为明显。
3.2水平地震力加速度系数
图5中c=0kPa,β=90°,φ=25°。描述了q和kh对K的影响。q=0kPa,Kh分别从0.0增加到0.2和0.3时,K分别增加39.0%和64.7%;q=40kPa,kh分别从0.0增加到0.2和0.3时,K分别增加19.3%和31.5%。这表明:与滑动体上部有附加荷载的挡土墙相比,水平地震力加速度对滑动体上部无附加荷载的挡土墙影响更为明显。

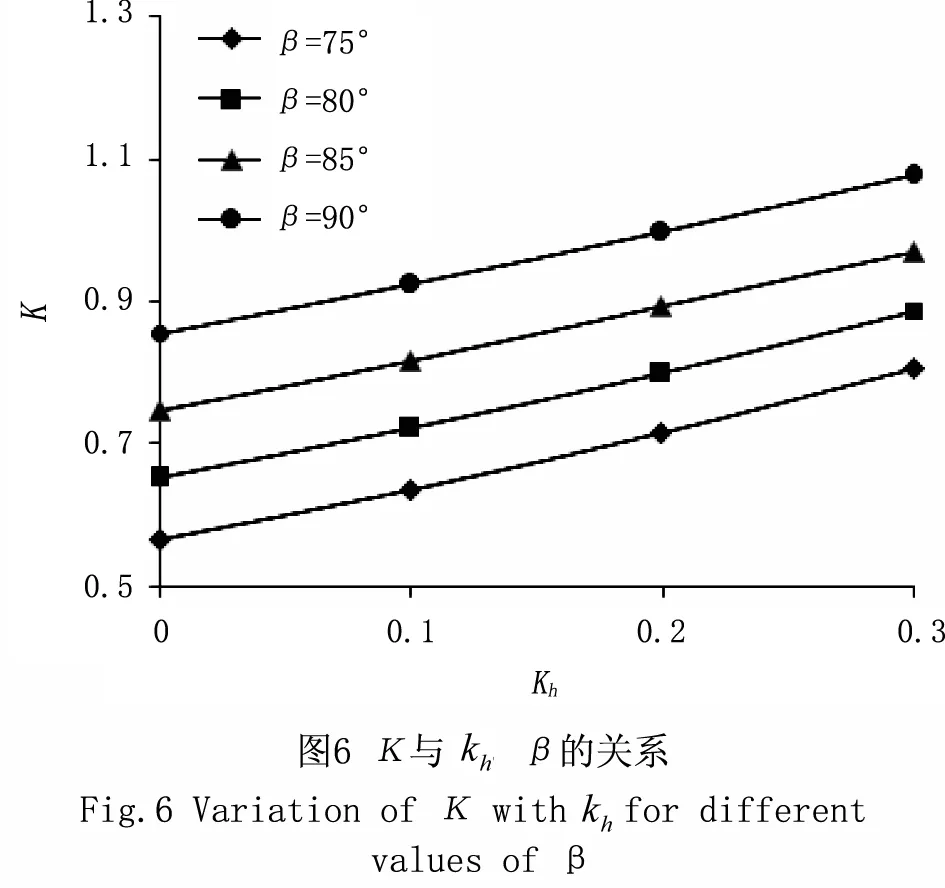
图6中c=0kPa,q=40kPa,φ=25°。描述了β和kh对K的影响,K随β的增加而减小。β=75°,kh分别从0.0增加到0.2和0.3时,K分别增加26.1%和42.2%;β=90°,kh分别从0.0增加到0.2和0.3时,K分别增加16.5%和25.7%。这表明:与竖直挡土墙相比,水平地震力加速度对倾斜挡土墙的影响更为明显。
3.3填土粘聚力
图7中kh=0.2,φ=25°,β=90°。描述了c和q对K的影响,K随c的增大而减小,随q的增加而增大。kh=0.2,q=0kPa,c分别从0kPa增加到10kPa和15kPa,K分别降低51.9%和77.3%;q=40kPa,分别从0kPa增加到10kPa和15kPa,K分别降低30.4%和46.5%。这表明:与滑动体上部有附加荷载的挡土墙相比,填土粘聚力对滑动体上部无附加荷载的挡土墙影响更为明显。

图8中kh=0.2,q=40kPa,φ=25°。描述了c和β对K的影响,K随β的增加而增大。β=75°,c分别从0kPa增加到10kPa和15kPa,K分别降低42.6%和63.9%;β=90°,c分别从0kPa增加到10kPa和15kPa,k分别降低29.2%和43.8%。这表明:与竖直挡土墙相比,填土粘聚力的变化对倾斜挡土墙的影响更为明显。

3.4滑动体上部荷载
图9中c=0 kPa,kh=0.2,φ=25°。描述了q和β对K的影响,K随β的增加而增大。β=75°,q分别从0 kPa增加到20 kPa和40 kPa,K分别增加23.4%和49.1%;β=90°,q分别从0 kPa增加到20 kPa和40 kPa,K分别增加31.1%和62.1%。这表明:与倾斜挡土墙相比,滑动体上部荷载的变化对竖直挡土墙的影响更为明显。


表1 三种方法下K的计算结果
为了验证新算法的准确性,用本文的方法与文献[4,11]的方法同时计算c=0 kPa、q=0 kPa、β=90°、γ=18 kN/m3和Fs=1.0的筋材总拉力值。由公式(8),得到计算结果k见表1,三种算法的结果基本一致,只有极小的差异,充分说明了本文计算方法的可靠性和有效性。
4 结论
1)土体内摩擦角越大,筋材拉力总值越小。因此,在安全系数内,加筋土挡土墙的地震稳定性随挡土墙后土体内摩擦角的增大而增大。
2)滑动体上部荷载对加筋土挡土墙的稳定性有很大影响。上部荷载越大,筋材拉力越大,加筋土挡墙的地震稳定性也会随之变差。
3)水平地震力加速度系数是影响加筋土挡墙的地震稳定性主要因素,随着水平地震加速度系数的增大,需要更大的筋材拉力来维持加筋土挡土墙的稳定性。
4)考虑回填土和上部荷载因素的影响,倾斜加筋土挡墙的地震稳定性比竖直挡墙的稳定性好。
[1]MONONOBE N.Considerations into earthquake vibrations and vibration theories[J].Journal of the Japanese Society of Civil Engineers,1924,10(5):1063-1094.
[2]OKABE S.General theory of earth pressure[J].Journal of the Japanese Society of Civil Engineers,1926,12(1):123-124.
[3]SHUKlA S K.Seismic active earth pressure from the sloping c- soil backfills[J].Indian Geotech,2013,43(3):274-279.
[4]SHAHGHOLI M.Horizontal slice method of analysis[J].Geotechnique,2001,51(10):881-885.
[5]蒋建清,杨果林.加筋土挡墙地震稳定性分析的水平条分方法[J].中国铁道科学,2009,30(1):36-40.
[6]LING H L,LESHCHINSKY D,PERRY E B.Seismic design and performance of geosynthetic-reinforced soil. structures[J].Geotechnique,2007,47(5):933-952.
[7]阮晓波,孙树林.加筋土挡墙地震稳定性影响分析[J].水利水电科技进展,2012,32(Z1):8-10.
[8]NIMBALKAR S S,CHOUDHURY D,MANDAL J N.Seismic stability of reinforced-soil wall by pseudo-dynamic method[J].Geosynth Int,2006,13(3):111-119.
[9]程亚男,孙树林,阮晓波,等.加筋土挡墙地震稳定性的拟动力分析[J].岩土力学,2013,34(12):3573-3579.
[10]汪益敏,张 晖,黎 寰,等.考虑地震时程的加筋土挡土墙动力分析[J].振动与冲击,2013,32(24):187-197.
[11]JTJ 015-1991,公路加筋土工程设计规范[S].
(责任编辑王利君)
Analysis of parameter influence on seismic stability of reinforced soil walls
WANG Enxi1, SUN Shulin1,2, CHEN Yiyang1,LIU Jun1, LIU Bo1,LI Fang3
(1.College of Earth Sciences and Engineering,Hohai University,Jiangsu Nanjing 211100, China;2.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering,Hohai University,Jiangsu Nanjing, 210098,China;3.JiangSu Provinice Nanjing Engineering Vocational College,Jiangsu Nanjing, 211135,China)
Aiming at the shortages of seismic design factors for retaining wall, the combination of pesudo-static and horizontal slice methods were used to analyze the seismic stability of reinforced soil walls, and the effect of various parameters including angle of internal friction, horizontal seismic loading, cohesion of the backfill, surcharge loading and inllination angle were examined. The results show that: The stability of a reinforced soil wall increases with the increase of horizontal seismic loading and surcharge loading, while it decreases with the increase of angle of internal friction and cohesion of the backfill. Under the same conditions, the inclined wall is more stable than the vertical wall.
reinforced soil walls;stability;parameter;pesudo-static method;horizontal slice method
2016-03-31
国家重点实验室开放研究基金资助项目(2005408911);留学回国人员科研基金资助项目(20071108);江苏省环境保护厅项目(201029)
王恩喜(1991-),男,山东郓城人,硕士,从事岩土地震工程方面的研究。
1673-9469(2016)03-0024-05
10.3969/j.issn.1673-9469.2016.03.005
TU476
A
