平面电路中的约束条件与电路方程的独立性分析
2016-11-07李福新
◆李福新
平面电路中的约束条件与电路方程的独立性分析
◆李福新
利用数学归纳法证明仅含有两端元件的平面电路中支路、结点、网孔之间的关系,并由此得出平面电路中方程的独立性原则,该原则是支路电流分析法的理论基础。
平面电路;基尔霍夫定律;数学归纳法
10.3969/j.issn.1671-489X.2016.03.156
1 序言
在直流电阻电路的分析计算方法中,支路电流法是以支路电流为求解变量的电路分析方法[1]。支路电流法是根据各个元件上的VAR(元件约束)和电路各结点的KCL、网孔的KVL(拓扑约束)关系,以电路中各条支路上的电流为未知量,建立数目足够且相互独立的方程组,通过求网孔电压KVL和结点的KCL结合列出足够且相互独立的方程组,并求解的过程。方法指出,可以根据电路中的结点数n,列出n-1个独立的电流方程;根据电路中的网孔个数m,列出m个独立的电压方程。这样,总的方程数(n-1)+m正好可以求解出电路中全部b条支路中的电路,即b=(n-1)+m。
考虑到拓扑约束证明的数学内容并非机电类工科学生的必修内容,且比较难掌握,在教学中通常只是让学生记住此结论,而并不加以证明。有学生对此提出疑问:“电路的支路条数b、网孔数m和结点个数n肯定满足以上关系吗?如果有特例,岂不是无法正确求解?”
为了解答学生的疑问,笔者首先用数学方法证明以上结论的正确性,并在此基础上讨论平面电路方程的独立性问题。
2 电路中的常用名词
先明确电路中的几个常用名词的概念,这一点很重要。因为在不同的依据中,某些名词概念的含义是不同的,特别是支路、结点的概念。本文中的支路是按照电路中同一电流习惯给出的,有别与网络拓扑分析中的定义[2]。
1)平面电路:对于任意扭动电路的分支,将之铺在一个平面上,若可以避免相交叉而又不连接的现象发生,则称该电路为平面电路。换言之,平面电路就是可以画在一个平面上而不使任何电路分支交叉的电路。本文中只讨论仅含有两端元件的平面电路,如图1平面电路所示。

图1 平面电路
2)支路(branch):电路中同一电流流过的分支电路全部。图1电路中共有六个电流i1、i2、i3、i4、i5、i6,故此有六条支路。
3)结点(node):电路中三条或三条以上支路的公共连接点。图1电路中有四个结点,分别是a、b、c和d,而e、f、g不是结点。
4)网孔(mesh):平面电路中的一个内部无任何支路的闭合回路。图1电路中有三个网孔,分别是回路a→b→d→e→a、b→c→f→d→b、a→g→c→b→a。
5)基尔霍夫电流定律(KCL):静态电路中,流经电路中任一结点的电流代数和恒等于0。
6)基尔霍夫电压定律(KVL):任意时刻,沿电路任一回路绕行一周,回路中各个元件上的电压的代数和恒等于0。
3 数学归纳法(Mathematical Induction)
数学归纳法是一种证明与自然数有关的命题的重要方法。一般的,证明一个与自然数n有关的命题P(n),有如下步骤:
1)证明当n取第一个值n0时命题成立,n0取0或1,或指定的某一具体数;
2)假设n=k(k≥n0,k为自然数)时命题成立,证明n=k+1时命题也成立;
3)综合前两步,对一切自然数n(n≥n0)都成立。
数学归纳法的三个步骤中,第一步是证明的奠基,第二步是递推的依据,这两个步骤都非常重要,缺一不可。
4 利用数学归纳法证明平面电路中的数学关系
根据以上所介绍的平面电路的基本概念及数学归纳法的证明步骤,若想证明b=(n-1)+m关系式对于任意平面电路都成立,不妨从m=1开始,电路如图2所示。此电路中n=0,b=1,显然满足关系式b=(n-1)+m。

图2 平面电路m=1
图2电路是通过增加一条新支路的方法,得到两个网孔的电路,即m=2。如图3电路所示,此电路中支路条数b=3,结点个数n=2,很明显也满足b=(n-1)+m。
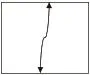
图3 平面电路m=2
依然通过增加新支路的方法,得到三个网孔电路,即m=3,将会出现三种不同的电路,分别如图4(a)(b)(c)所示。其中,图4(a)中电路的结点数不变,即新增的支路是由原电路中的两个结点之间接入,即n=2,此时支路数变为b=3+1=4;图4(b)中电路的结点数n=3,即新增的支路是由原电路中的一个结点和增加一个新的结点(可以理解为原电路中的某一条支路上的一个点变为结点)之间接入,此时新电路的支路数b=3+1+2-1=5;图4(c)中电路的结点数n=4,是由增加的连个新结点之间引入一条支路,则新电路支路数b=3+1+4-2=6。
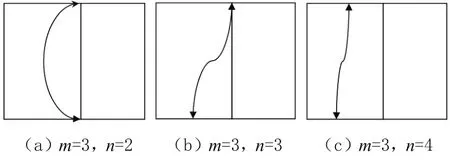
图4 两个网孔的平面电路
通过计算可以得出结论:三种情况中,均满足关系式b=(n-1)+m。
现在假设某平面电路中的网孔数满足m=μ(μ≥3,μ为自然数),结点数n=ν(ν为自然数)时,电路中支路条数b=(n-1)+m=(ν-1)+μ关系式成立,则通过增加一条新支路的方法使得网孔数增加1,即m=μ+1。如前所述分析可知,新电路会有三种情况出现:图5(a)电路中n=ν,b=(ν-1)+ μ+1=(n-1)+m;图5(b)电路中n=ν+1,b=(ν-1)+μ+1+2-1=(n-1)+m;图5(c)电路中n=ν+2,b=(ν-1)+μ+1+4-2=(n-1)+m。
可见,对与网孔数为m=μ+1的平面电路,上述关系式依然成立。由以上分析,可知结论b=(n-1)+m对所有平面电阻电路均适用。

图5 两个网孔的平面电路
5 平面电阻电路中方程的独立性
所谓的独立方程,即任意一个方程都不能由所列的其他方程组合得到[4]。事实上,在一般情况下,对于有n个结点、b条支路的平面电路,可以列出n-1个独立的KCL方程,这是因为对于n个结点中的前n-1个,可以分别列出独立的KCL方程,而对于第n个结点,流入的电流其实可以表示为其他所有结点流出电流之和,流出的电流可以表示为其他所有结点流入电流之和,故此并非独立方程;而在所列的各KVL方程中,可以确定的是以m个网孔为回路所列的KVL方程一定是相互独立的,即b-(n-1)=m个,其他非网孔的回路所列的KVL方程可以由这m的独立方程相加得到。因此,通过KCL和KVL所列的(n-1)+m个独立方程,再加上VAR元件约束条件,可以求解出来任一平面电阻电路中全部b条支路上的电流。
[1]陆国和.电路与电工技术[M].3版.北京:高等教育出版社,2010.
[2]陈自力,刘学军.克希霍夫独立方程数定理的证明[J].电工教育,1995(3).
G 712
B
1671-489X(2016)03-0156-02
作者:李福新,天津中德职业技术学院基础课部讲师(300350)。
