基于计数辅助树的蒙特卡罗粒子输运计算大规模计数方法

张　澍　郝丽娟　宋　婧　吴　斌　孙光耀

1（中国科学技术大学　核科学技术学院　合肥　230027）2（中国科学院核能安全技术研究所　中国科学院中子输运理论与辐射安全重点实验室　合肥　230031）

基于计数辅助树的蒙特卡罗粒子输运计算大规模计数方法

张澍1,2郝丽娟2宋婧2吴斌2孙光耀2

1（中国科学技术大学核科学技术学院合肥230027）2（中国科学院核能安全技术研究所中国科学院中子输运理论与辐射安全重点实验室合肥230031）

传统的蒙特卡罗粒子输运计算程序在粒子每一步模拟结束后，通过遍历所有计数器来判断当前粒子所在栅元是否需要进行计数，该过程耗时随计数器数量的增加近似线性增长，当计数器数量较大时，计数耗时远高于输运耗时。本文发展了一种基于计数辅助树的大规模计数加速方法，建立了与几何栅元一一对应的树形结构，并在节点中存储了相应栅元的计数信息，通过当前粒子所在栅元的几何信息从树中快速读出对应的计数器。为了验证该方法的有效性，基于Hoogenboom全堆基准例题测量了不同计数器数量下的计算耗时。测试结果显示本文方法能有效地提高大规模计数问题的计算效率。

蒙特卡罗，粒子输运，计数辅助树，大规模计数

蒙特卡罗粒子输运方法由于能够对任意复杂的三维几何模型和物理现象进行精确的描述和处理，在核能系统核设计与辐射安全评价等领域得到了广泛的应用。随着现代反应堆设计中对计算精度要求的提高，包含百万甚至千万量级计数栅元的全堆芯高保真高精细模拟成为了研究的热点之一。国内外很多蒙特卡罗输运程序，如MCNP （Monte Carlo N Particle Transport Code）［1］、OpenMC （OpenMC Monte Carlo Code）［2］、RMC （Reactor Monte Carlo Code）［3］、JMCT （J Monte Carlo Transport Code）［4］等，都对此方向进行了大量的研究。

蒙特卡罗程序在粒子每一步模拟结束后，需要判断当前粒子所在栅元是否需要进行计数。传统的判断方法需要遍历所有计数器，其时间复杂度为O（N），其中N为计数器的数量。Veen等［5］指出由于MCNP5对栅元计数应用了传统的顺序遍历方法，其计数耗时随着计数器栅元数量的增加近似线性增长，如图1所示。如果在单个CPU上使用MCNP5对包含约6×106计数的反应堆基准例题进行计算，模拟100代，每代105个粒子，计算耗时会高达4×106min。因此，当计数器数量达到百万量级时，需要应用高效的计数方法以保证输运计算的效率。最高效的计数方法为映射法，即建立从栅元编号到计数器的映射，根据粒子当前所在栅元的编号，可直接通过映射关系获取对应的计数器，其时间复杂度为O（1）。但这种映射关系要求每个栅元在计算模型中唯一存在。

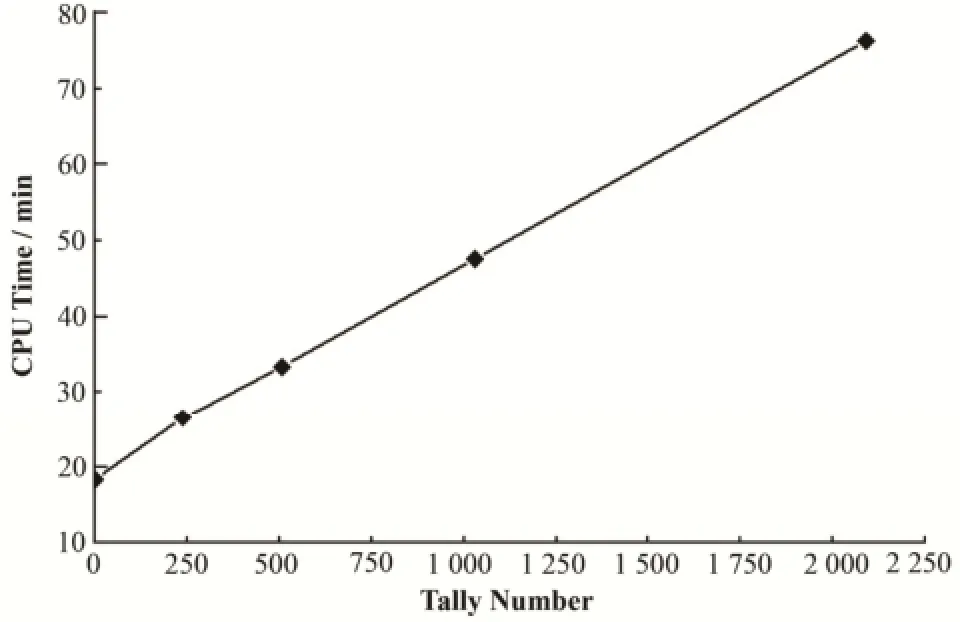
图1　MCNP5计算时间随计数器数量的变化［5］Fig.1　Run time of MCNP5 changes with the number of tallies［5］.

然而大规模计数问题常见于通过重复结构描述的裂变堆堆芯模型，蒙特卡罗程序对重复结构栅元有两类处理方法：一为重复结构栅元共用一套几何描述，但栅元编号保持独立，因此可根据映射法保证高效的栅元计数；二为重复结构栅元编号并不保持独立，需要根据栅元在几何结构中的层级关系来唯一确定，其优点在于内存开销相对较小，但无法从栅元编号直接映射到对应的计数器。针对此问题，RMC程序提出了基于栅元映射、哈希表和层级标记的计数加速方法［6］，将栅元的几何信息映射为一个整型变量，用单调整数序列的二分查找替换了原本的顺序查找，并通过哈希表缩小了二分查找的范围，显著提高了计数效率。但该方法只有在使用了层级标记，即预先指定计数栅元为几何结构的固定层级时才能达到最佳加速效果。

通过充分利用模型的几何信息，本工作发展了一种基于计数辅助树的大规模计数方法，由栅元几何信息直接映射到对应的树形节点获取计数器信息，提高了计数的效率，并基于FDS团队自主研发的超级蒙特卡罗核计算仿真软件系统SuperMC［7−8］实现了该方法。SuperMC是一款具有完全自主知识产权的通用、智能、精准的核系统设计优化与安全评价软件，可应用于反应堆的设计［9−11］和分析［12−13］、核材料［14−15］辐照损伤分析等领域。SuperMC目前已发展复杂系统自动精准建模［16］等关键技术，通过了2000余个国际基准模型（国际热核聚变实验堆［17］、国际临界安全基准评价手册［18］等）及实验的验证与确认。

1　树形结构创建方法

本文所创建的树形结构类似于不使用重复结构描述的模型几何结构，树的每个节点与模型的每个几何栅元一一对应，根节点对应世界体栅元，叶子节点对应最底层的重复结构栅元。其中，世界体栅元是包围模型整体空间的一个实体，用于描述模型中未定义的空间。每个节点使用两个顺序容器（vector）分别记录了该节点对应的几何栅元的所有计数器索引和该节点对应的几何栅元的所有子栅元对应子节点的指针。本文将这种树形结构的描述方式称为独立节点描述。

在树形结构的构建中，首先根据模型的几何结构通过一个递归函数建立“树”，将每个节点的所有子节点的指针存储至vector容器中，完成“树”的建立后，再遍历所有的计数器，将其索引添加到对应节点的计数器列表中。

上述独立节点描述的树形结构，在全堆芯精细计算中，可能需存储数百万个vector容器，每个容器都在进程的堆上分配了一段内存。在x86环境下，每个空的vector容器本身需要16 byte的内存开销，另外，对于C++编写的代码，每次内存开辟都需要一些额外的内存开销（4−32 byte）［19］。所以，大量的容器带来计数信息以外的大量额外内存开销。由于全堆芯的蒙特卡罗计算通常受到计算机内存的限制，因此有必要尽可能降低树形结构的内存使用。

为避免大量vector容器带来的额外内存开销，对上述树形结构进行了优化，将树中的所有信息压缩进两个vector容器，分别为存储了所有计数信息的tally_vector和存储了所有节点间拓补信息的tree_vector，如图2所示。SuperMC中的计数器数据结构包含两级层次关系，在输入文件中可定义若干个计数卡（tally），每个计数卡里又可定义若干独立的计数器（bin）。因此每个计数器可通过其tally id和 bin id唯一确定，相应地在tally_vector中，连续地存储了每个节点所对应的所有计数器的索引。在tree_vector中，每个节点用三个整型变量描述，分别是：

1） first child：该节点的第一个子节点在tree_vector中存储位置的索引。默认值是−1，表示该节点没有子节点。

2） first tally：该节点对应的计数器在tally_vector中存储位置的起始索引。默认值是−1，表示该节点不对应任何计数器。

3） last tally：该节点对应的计数器在tally_vector中存储位置的末尾索引。

在tree_vector中，第一个节点对应的是世界体，每个节点的子节点都是连续存储的。这两个vector可通过对原始的树形结构的广度优先搜索进行构建。在tally_vector和tree_vector构建完成后，便可以将原始的树形结构删除以释放其占用的内存。

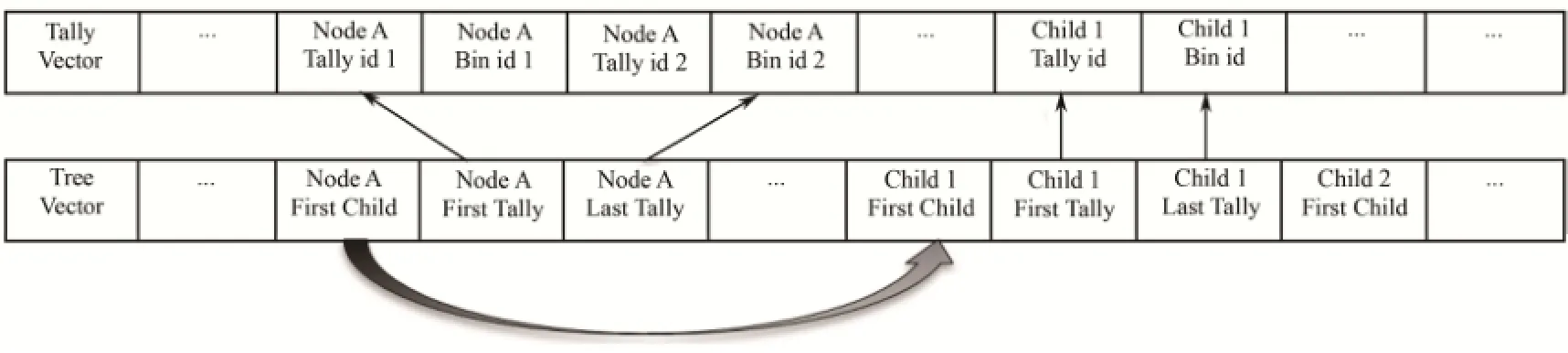
图2　tally_vector和tree_vector的结构Fig.2　Structure of tally_vector and tree_vector.

2　基于树形结构的计数流程

在层级空间的几何描述方法的基础上，当前粒子所在栅元的几何信息由一系列层次不同的栅元组成：

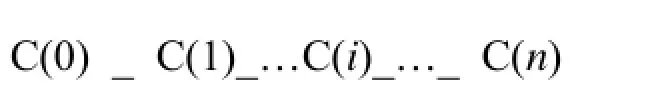
其中：C（i）为指向某个栅元的指针，同时C（i）为C（i+1）的父栅元；C（0）为世界体；C（n）为当前栅元。

基于树形结构的计数详细流程如图3所示，其中的关键在于从当前栅元的几何信息映射到对应的树形节点。通过遍历当前栅元的几何信息，从世界体栅元出发，可以在tree_vector中找到每一层级的栅元所对应的节点。当访问到几何信息中最后一个栅元时，就可以根据当前所找到的tree_vector节点，从tally_vector中读出所对应的计数器信息。上述流程只需要遍历一次该栅元的几何信息，故计数效率高，对计算耗时的影响小。以核素反应率计数为例，在每一步输运完成后，通过tree_vector和tally_vector可快速找出当前栅元对应的计数器，再从数据库读出相应的反应截面，计算出对反应率的贡献，最后根据粒子能量计算出所属能群，将计数结果累加到计数器中的相应位置。

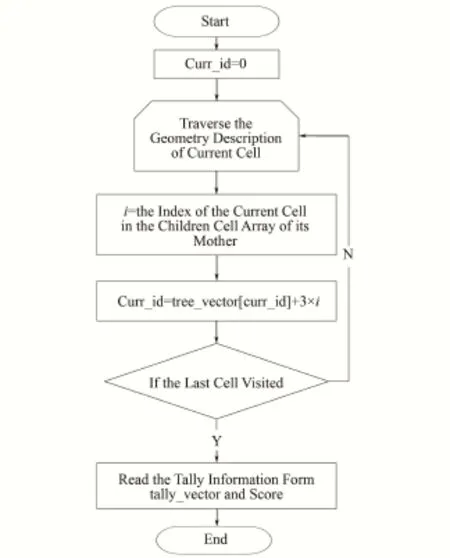
图3　基于计数辅助树的计数流程Fig.3　Tally assist tree-based tally procedure.

3　测试与结果分析

为了验证文中算法的有效性，采用Hoogenboom全堆基准例题［20］进行数值测试。该模型以大型压水堆堆芯为原型，被用来检验蒙特卡罗输运程序的全堆计算能力，其几何结构如图4所示。堆芯包含241个燃料组件，每个燃料组件包含17×17个燃料棒，每根燃料棒轴向划分为100层，对全堆芯计数时，计数器的个数为6 362 400。计算条件为每代10 000个粒子，共计算150代，其中非活跃代为50代。为比较计数方法的性能，只统计了活跃代的计算时间。虽然对于该例题，本文的计算规模无法得到收敛的计算结果，但可以反映计数耗时随计数器数量的变化趋势。

图4　Hoogenboom堆芯（a）和组件（b）截面图［20］Fig.4　Cross section of reactor of Hoogenboom core （a） and a fuel assembly （b）［20］.

针对该例题所建立的计数辅助树，如果通过独立节点来描述，在x86环境下的内存开销为395.2MB，x64环境下内存开销为692.8 MB。而使用tally_vector和tree_vector描述时，内存开销仅为133.5 MB。与此相对，如果在SuperMC中将重复结构栅元全部展开，所有栅元保持独立，在x64环境下，SuperMC中单个栅元的内存开销为448 byte，全堆芯6×106栅元的内存总开销会达到约2.7 GB。

表1列出了基于计数辅助树的计数方法和顺序查找方法的计算时间对比结果。总计算时间由输运计算耗时和计数耗时两部分组成，计数器数量为0时的计算时间可看作纯输运耗时。图5给出了这两种计数方法计算时间随计数器数量的变化关系。从图5中可以看出，顺序查找计数方法的计算时间随计数器数量线性增长，当计数器数量为2000时计数耗时便已达到输运计算耗时的46.5倍。若根据图5中的线性关系进行估计，当进行全堆芯计算时，总耗时将高达1.66×106min，无法直接测量。而使用本文发展的树形结构计数，计算时间几乎不受计数器数量的影响，对全堆芯进行计数的计数耗时仅为0.442 min，约为输运耗时的4%。本文方法已成功应用于SuperMC的Hoogenboom全堆芯计算校验［21］，得到了全堆芯收敛的计算结果。同时本文方法与RMC程序提出的计数方法［6］相比，在计算规模相似时，计数的耗时也相近，具有同样良好的加速效果。

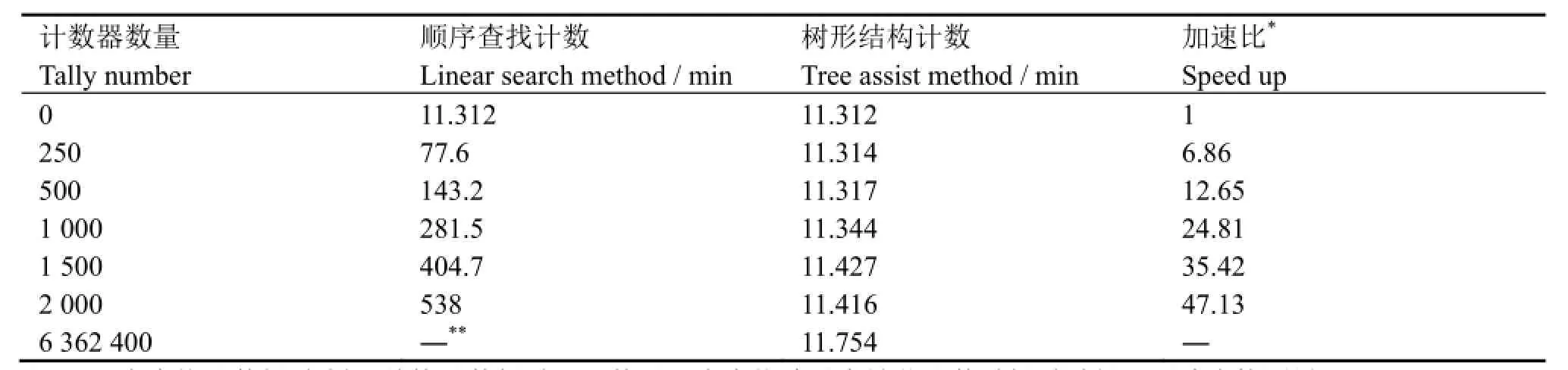
表1　两种计数方法计算时间对比Table 1　Run time comparison of two tally methods.

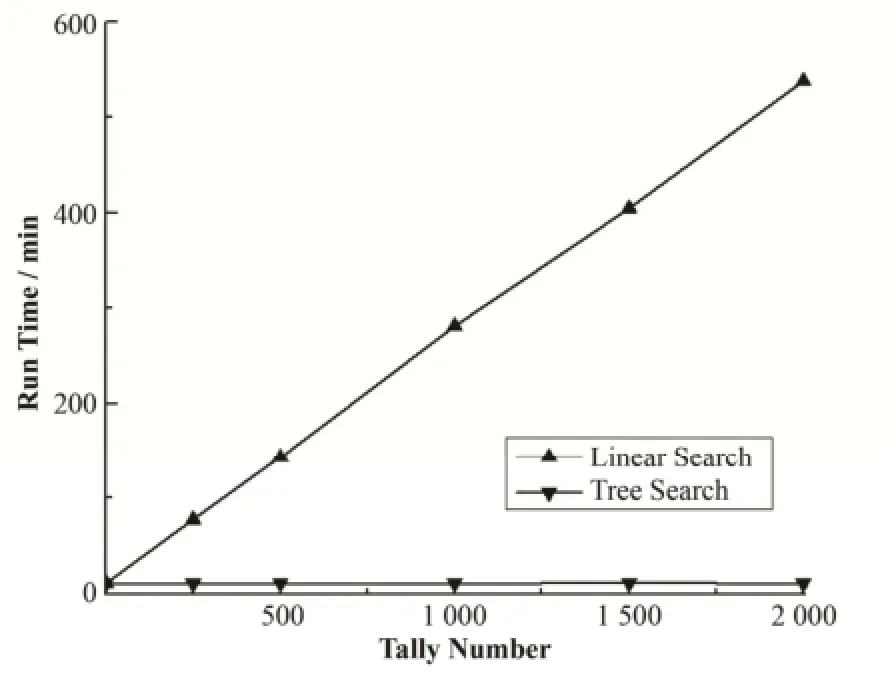
图5　计算时间随计数器数量的变化关系Fig.5　Relationship between run time and tally number.

4　结语

本文提出了一种基于计数辅助树的蒙特卡罗大规模计数加速方法。根据Hoogenboom反应堆基准例题的测试表明，在对全堆芯6×106栅元进行计数时，计数耗时仅为输运耗时的4%，与传统通过遍历查找计数器的方法相比，计算效率提升明显，可有效应用于高保真全堆芯输运模拟。

致谢本文开展研究工作中，得到了FDS团队其他成员的大力支持，在此深表感谢！

1 X-5 Monte Carlo Team. MCNP - a general Monte Carlo N - particle transport code［M］. Los Alamos Scientific Laboratory, 2003

2 Romano P K, Forget B. The OpenMC Monte Carlo particle transport code［J］. Annals of Nuclear Energy, 2013, 51（1）: 274−281. DOI: 10.1016/j.anucene.2012.06.040

3 Wang K, Li Z G, She D, et al. RMC-a Monte Carlo code for reactor core analysis［J］. Annals of Nuclear Energy, 2015, 82: 121−129. DOI: 10.1016/j.anucene.2014.08.048

4 邓力, 李刚, 张宝印, 等. JMCT蒙特卡罗中子-光子输运程序全堆芯pin-by-pin模型的模拟［J］. 原子能科学技术, 2014, 48（6）: 1061−1066

DENG Li, LI Gang, ZHANG Baoyin, et al. Simulation of full-core pin-by-pin model by JMCT Monte Carlo neutron-photon transport code［J］. Atomic Energy Science and Technology, 2014, 48（6）: 1061−1066

5 Veen D V, Hoogenboom J E. Efficiency improvement of local power estimation in the general purpose Monte Carlo code MCNP［J］. Progress in Nuclear Science and Technology, 2011, 2（1）: 866−871

6 She D, Qiu Y. Improved methods of handling massive tallies in reactor Monte Carlo code RMC［R］. Proceeding 2013 International Conference on Mathematics & Computational Methods Applied to Nuclear Science and Engineering, Sun Valley, Idaho, May 5−9, 2013

7 Wu Y, Song J, Zheng H Q, et al. CAD-based Monte Carlo program for integrated simulation of nuclear system SuperMC［J］. Annals of Nuclear Energy, 2015, 82（1）: 161−168. DOI: 10.1016/j.anucene.2014.08.058

8 Wu Y, FDS Team. CAD-based interface program for fusion neutron transport simulation［J］. Fusion Engineering and Design, 2009, 84（7−11）: 1987−1992. DOI: 10.1016/j.fusengdes.2008.12.041

9 Wu Y, FDS Team. Conceptual design activities of FDS series fusion power plants in China［J］. Fusion Engineering and Design, 2006, 81（23−24）: 2713−2718. DOI: 10.1016/j.fusengdes.2006.07.068

10 Wu Y, Jiang J, Wang M, et al. A fusion-driven subcritical system concept based on viable technologies［J］. Nuclear Fusion, 2011, 51（10）: 103036. DOI: 10.1088/0029-5515/ 51/10/103036

11 Qiu L, Wu Y, Xiao B. A low aspect ratio tokamak transmutation system［J］. Nuclear Fusion, 2000, 40（3Y）: 629−633. DOI: 10.1088/0029-5515/40/3Y/325

12 Wu Y, FDS Team. Design analysis of the China Dual-Functional Lithium Lead （DFLL） test blanket module in ITER［J］. Fusion Engineering and Design, 2007, 82（1）: 1893−1903. DOI: 10.1016/j.fusengdes.2007.08. 012

13 Wu Y, FDS Team. Conceptual design of the China fusion power plant FDS-II［J］. Fusion Engineering and Design, 2008, 83（1）: 1683−1689. DOI: 10.1016/j.fusengdes.2008. 06.048

14 Wu Y, FDS Team. Fusion-based hydrogen production reactor and its material selection［J］. Journal of Nuclear Materials, 2009, 386−388: 122−126. DOI: 10.1016/ j.jnucmat.2008.12.075

15 Wu Y, FDS Team. Design status and development strategy of China liquid lithium-lead blankets and related material technology［J］. Journal of Nuclear Materials, 2007, 367−370: 1410−1415. DOI: 10.1016/j.jnucmat.2007.04. 031

16 Li Y, Lu L, Ding A, et al. Benchmarking of MCAM4.0 with the ITER 3D model［J］. Fusion Engineering and Design, 2007, 82（15−24）: 2861−2866. DOI: 10.1016/ j.fusengdes.2007.02.022

17 Song J, Sun G Y, Chen Z P, et al. Benchmarking ofCAD-based SuperMC with ITER benchmark model［J］. Fusion Engineering and Design, 2014, 89（1）: 2499−2503. DOI: 10.1016/j.fusengdes.2014.05.003

18 Zhang B H, Song J, Sun G Y, et al. Criticality validation of SuperMC with ICSBEP［J］. Annals of Nuclear Energy, 2016, 87: 494−499. DOI: 10.1016/j.anucene.2015.10.004

19 Andrei A. Modern C++ design: generic programming and design patterns applied［M］. Boston: Addison-Wesley, 2001

20 Hoogenboom J E, Martin W R. The Monte Carlo performance benchmark test - aims, specifications and first results［R］. International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Rio de Janeiro, Brazil, May 8−12, 2011

21 刘鸿飞, 张彬航, 张澍, 等. 基于Hoogenboom基准模型的SuperMC全堆芯计算能力校验［J］. 核技术, 2016, 39（4）: 040604. DOI: 10.11889/j.0253-3219.2016.hjs.39. 040604

LIU Hongfei, ZHANG Binhang, ZHANG Shu, et al. Full reactor core calculation performance validation of SuperMC based on Hoogenboom benchmark［J］. Nuclear Techniques, 2016, 39（4）: 040604. DOI: 10.11889/j. 0253-3219.2016.hjs.39.040604

Tally assist tree-based method for scoring massive tallies in Monte Carlo particle transport calculation

ZHANG Shu1,2HAO Lijuan2SONG Jing2WU Bin2SUN Guangyao2

1（School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230027, China）
2（Key Laboratory of Neutronics and Radiation Safety, Institute of Nuclear Energy Safety Technology, Chinese Academy of Sciences, Hefei 230031, China）

Background: Traditional Monte Carlo particle transport calculation codes traverse all the tally cards to find which tallies should be scored at the end of each simulation step. The run time of this procedure almost grows linearly with the number of total tally number. When the tally number is large, the tally procedure costs far more time than the transport calculation. Purpose: This paper proposed a tree-based method for scoring massive tallies. Methods: The method builds a tally assist tree that all the nodes map one-for-one to the geometry cells. All the tally information read from the input file is stored in the tree. At the end of each simulation step, by mapping the geometry information of the cell where the particle is currently in to a node in the tree, the tallies need to be scored is directly retrieved from the node. Results: To test the proposed method, the run time of the Hoogenboom benchmark reactor model with different tally numbers is measured. Conclusion: The results show that this method can improve thecomputation efficiency of massive tally problems.

Monte Carlo, Particle transport, Tally assist tree, Massive tallies

SUN Guangyao, E-mail: guangyao.sun@fds.org.cn

TL329.2

10.11889/j.0253-3219.2016.hjs.39.100502

中国科学院战略性先导科技专项（No.XDA03040000）、国家自然科学基金（No.11305203）、国家磁约束核聚变能发展研究专项（No.2014GB1120000）资助

张澍，男，1990年出生，2011年毕业于中国科学技术大学，博士研究生，从事蒙特卡罗粒子输运研究工作，核能科学与工程专业

孙光耀，E-mail: guangyao.sun@fds.org.cn

Supported by Strategic Priority Research Program of Chinese Academy of Sciences （No.XDA03040000）, National Natural Science Foundation of China（No.11305203）, National Special Program for ITER （No.2014GB1120000）First author: ZHANG Shu, male, born in 1990, graduated from University of Science and Technology of China in 2011, doctoral student, focusing on Monte Carlo particle transport, major in nuclear energy science and technology

2016-05-26，

2016-07-07