变电站容性设备介损在线监测数据压缩与预处理方法

沈显庆，　段小龙

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)



变电站容性设备介损在线监测数据压缩与预处理方法

沈显庆，段小龙

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

介质损耗角是反映变电站容性设备绝缘程度的重要指标，在线监测处理方法采用数字化测量技术。依据绝缘特性的老化机理，监测数据具有一定的分散性和冗余性，因此，提出采用压缩比可变的嵌入式零树小波算法，对数据进行有效的压缩，提高信息管理的效率；利用最优相关滤波电路，滤除锯齿状波动和剔点等虚假信号，并将此信号转换成频域信号，通过小波重构方法进行特征值的提取。通过仿真分析验证，结果表明：对特征值的提取，可以提高容性设备绝缘诊断的准确性，实验验证该方法可行。

嵌入式零树小波算法； 最优相关滤波； 小波重构； 介质损耗角； 在线监测

0　引　言

根据绝缘特性的老化机理，变电站容性设备绝缘特性的变化非常缓慢，尽管数据具有一定的分散性，但波动仍在一定范围内，说明监测数据具有冗余性。加上需要监测的量和点数较多，如果能够发现数据展现的规律性，对数据进行有效的压缩，将提高信息管理的效率；通过对特征值的有效提取，有助于提高绝缘诊断的准确性[1-4]。针对变电站容性设备在线监测的特性，常规的数据压缩方法，如Huffman编码、算数编码和自适应 Huffman编码,均存在的共性问题是数据的相关性大，压缩比不容易改变，压缩速度慢等。笔者试图采用改进的嵌入式零树小波算法，利用小波分解系数，通过选取不同阈值及变化压缩比的方式，有效地解决这些问题。

在线监测数据稳定性、重复性较差，必须对在线数据进行预处理，剔除测量结果中的不良数据和虚假数据。利用3δ准则和自适应广义形态滤波方法判断异常数据[5]，前者可以减少脉冲性干扰和采样元件引起的粗大误差对在线监测数据的影响，但存在判断不准确或遗漏；后者对介损在线数据中存在的加性白噪声和调制性噪声有较好的抑制作用，但没有考虑其他因素的影响，难以保证设备绝缘诊断的可靠性[6]。为此，文中在硬件方面采用最优相关滤波电路剔除抖动带来的相位噪声，采用小波重构方法，选取合适的阈值实现对数据的预处理。

1　容性设备介损在线监测数据模型

容性设备绝缘老化趋势非常缓慢，介损在线监测数据可以看作是一个在时间上为连续变量的离散数据序列。由于设备绝缘状况受到环境温度、湿度及季节周期性变化、电力设备回路负荷变动的影响，也会引起其介损值的相应变化。此外，信号传输、电磁干扰等影响随机性很强，在序列上表现为锯齿状波动和剔点，可以视为数据中还存在一定量的附加白噪声和脉冲性噪声，为此考虑各种影响介损数据的因素，构建其模型[7]：

tanδ(t)=tanδ0(t)+Δtanδr(t)+Δtanδw(t)+

Δtanδl(t)，

(1)

式中：tanδ(t)——实际介损监测数据时间序列；

tanδ0(t)——反映绝缘基本特性，呈缓慢递增趋势，可考虑近似为tanδ(t)的直流分量；

Δtanδw(t)——反映气象因素影响，可认为是tanδ(t)的低频分量；

Δtanδr(t)——反映各种随机干扰的影响；

Δtanδl(t)——反映回路负荷变动影响，可认为是tanδ(t)的低频分量。

对介损在线监测数据进行预处理，主要是从监测数据序列中剔除Δtanδr(t)，即对数据进行消噪处理，有助于提高诊断的有效性。

2　嵌入式零树小波压缩算法

小波变换是一种变分辨率的时频联合分析方法，符合在实际应用中高频信号持续时间短、低频信号持续时间较长的自然规律，尤其适合突变信号的检测和非平稳信号序列的分析。

设正交小波基的滤波器系数分别为hk和gk，尺度函数为φ(t)，其二尺度方程为

(2)

由式(2)定义：

(3)

式中：{un(t)}——由小波包确定的函数集合；

通过正交小波包的分解，可以降低在相同尺度上的小波系数之间的关联性，但有较强的相关性在异同的小波系数之间存在。经过正交小波包的变换，它的系数呈树状结构，将根部的系数看作父系数，它的每个树枝都有两个分支，从而构成树结构的一维小波系数。

首先，利用连续累计量化方式，设定量化层的量化阈值T0,T1,…,TN-1，使得一切小波系数xj，初始阈值T0符合|xj|<2T0,max|xj|>T0，后面的阈值满足Ti=Ti-1/2。随着量化层数的增多，量化结果的输出越来越准确，而量化阈值和压缩比则成负相关性。

其次，进行量化编码，如图1所示。对于一个确定的阈值T，若小波系数的绝对值大于该阈值，则重要，反之则不重要。在编码过程中，用PS代表正重要系数，此时小波系数xj>T；用NS代表负重要系数，此时小波系数xj<-T；用ZR代表小波系数下的零树根，此时小波系数的绝对值以及子系数都小于阈值；用IZ代表小波系数下的孤立零，此时小波系数的绝对值都小于阈值，但存在个别子系数大于阈值。

图1　小波系数编码数据流程

最后，进行量化。量化过程的量化编码需按次序进行，连续累计量化方法的量化层包括两个量化过程，即主量化过程(量化主要系数)和次量化过程(剩余系数)。在主量化过程中，小波系数的重要性编码主要依据阈值序列的顺序，编码过程中会产生两个独立的序列：主序列和从序列。编码之前，一切小波系数在主序列中，而从序列不包含小波系数，编码中，如果某个小波系数为重要系数，接着判定此系数的符号，然后依照编码模型编码。所有为重要系数的小波系数将置在从序列中，主序列中的重要系数置零，保证一个系数一次编码。次量化过程在主量化过程后，主要对加入到从序列的小波系数作一个外加的精度位截短，使精度满足要求，数据量也减少了，接着进程将这个阈值减半，继续主量化过程，继而重复上述过程。编码的逆过程是解码。

3　基于滤波思想的预处理及数据提取方法

依据容性设备介损在线监测数据模型，选择合适的低通滤波器，滤除高次谐波和各种随机干扰分量，得到绝缘特性基本变化趋势；从时域角度分析，高次谐波和各种随机干扰分量的变化周期远远小于绝缘基本特性变化周期。因此，选用宽度合适的平滑滤波器，亦能将数据中的噪声分量消除。

3.1最优相关滤波测量谐波方法

3.1.1最优相关滤波检测相位的原理

实际工作中的电网有高次谐波各种随机信号的干扰。所以依据电网实际情况，建立数学模型[8]：

u(t)=[1+α(t)]U1msin(ωt+φu)+

(4)

i(t)=[1+β(t)]I1msin(ωt+φi)+

(5)

式中：u1(t)、i1(t)——基波u1(t)=U1msinωt,

i1(t)=I1msin(ωt+φi)；

δ——介质损耗角，δ=π/2-φi；

ξ(t)、η(t)——加性噪声，与u(t)、i(t)不相关；

α(t)、β(t) ——调制性噪声。

为提取没有噪声和高次谐波的噪声信号，对基波分量的正余弦信号进行同步采样，可以消除各种噪声及高次谐波的影响，提高测量精度。最优相关滤波检测相位电路如图2所示。

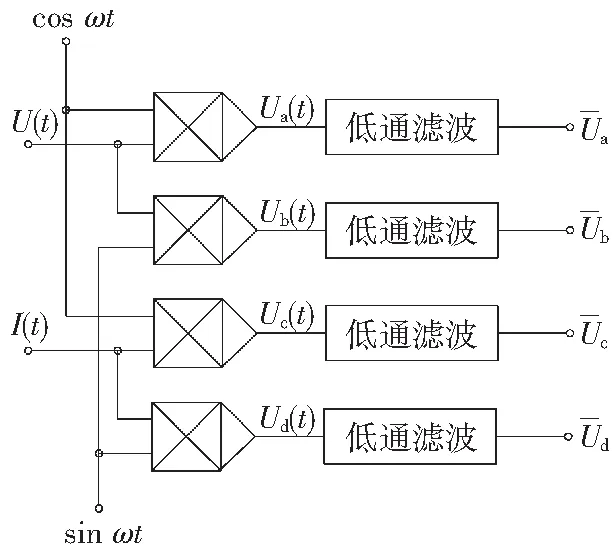
图2　最优相关滤波检测相位电路原理

Fig. 2Blockofmeasurementonphasecircuitbasedonoptimizationcorrelationfilter

假设调制性噪声为零，由式(4)、(5)及图2可得：

1/2U1msinφuE[cos 2ωt]+

U1mcosφuE[sinωtcosωt]+

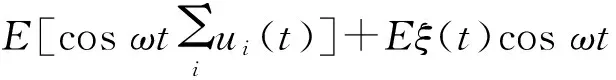
(6)

(7)

介质损耗角

δ=π/2-(φi+φu)。

3.1.2调制性噪声的处理

调制性噪声使电网的电压和电流产生很大的波动，如不正确处理，将使测量结果产生很大的误差，甚至没有意义。考虑调制性噪声影响时，基波信号可以写成:

u1(t)=[1+α(t)]U1msin(ωt+φu)，

(8)

i1(t)=[1+β(t)]I1msin(ωt+φi)。

(9)

电压路乘法器输出信号中基波信号u1(t)与标准余弦、正弦信号相乘的输出信号为：

ua1(t)=u1(t)cosωt，

(10)

ub1(t)=u1(t)sinωt，

(11)

把式(7)代入式(10)得

ua1(t)=1/2U1msinφu+1/2U1mα(t)sinφu+1/2U1msinφucos 2ωt+1/2U1mcosφusin 2ωt+1/2U1mα(t)cosφusin 2ωt+1/2U1mα(t)×sinφucos 2ωt。

(12)

调制性噪声α(t)的主要成分是频率远小于50 Hz的低频噪声，α(t)sin 2ωt、α(t)cos 2ωt是被α(t)调制的中心频率在2ω处的调制信号。ua1(t)经低通滤波后，式(12)中的第3、4、5、6项将被滤除，同时高次谐波的调制性噪声也将被滤除。由于α(t)可能包含频率极低的成分，而低通滤波器的截止频率又不可能设计的无限小，所以α(t)不能被完全滤除。令其经滤波器后变为α′(t)，若两路滤波器参数相同，滤波器的输出为：

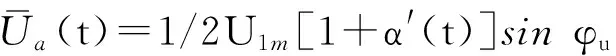
(13)

(14)

3.2基于小波变换的趋势提取方法

最优相关滤波在对调制性噪声滤波时，虽然不影响相位的测量，但仍有部分噪声进入系统，产生频谱泄漏和栅栏效应。为此，在硬件滤波的同时，还需要软件滤波，对数据进行平滑处理。文中采用小波消噪原理，通过小波分解和重构，并合理设置阈值的方式进行消噪。

采用门限阈值形式对小波系数进行处理，将噪声部分置零，或者减小到一个合适的值。处理完小波系数之后，对小波进行重构，噪声部分已被消除。

4　仿真分析

为验证压缩算法和预处理算法，数据取自哈东变电所。图3为原始数据和在选择不同阈值时的压缩效率，明显看出，重构信号与原始信号之间的误差随着阈值的逐渐增大而增大，经过压缩的数据亦可反映原始信号的特点。

图4为处理带有噪声的不同层次下的低频信号与原始数据的在线监测数据的效果，可以看出不同重构下，还原信号的能力不同，重构层次越多，还原信号的能力越强，算法需要的时间越多，在实际应用中还要和压缩阈值层次匹配。

图5为处理带有噪声的最优相关滤波与原始数据的在线数据监测效果。由于最优相关滤波在测量方法上，利用矢量正交分解，在测量原理上能够完全剔除加性噪声和调制性噪声，但要求低通滤波器的截止特性要好。

图6a为原始信号(一个带有突变点的正弦波信号)、图6b为带有噪声信号(原始信号叠加噪声)在小尺度j为1、2及固定阈值时的仿真波形。从图6中可以看出，利用小波变换的时频局部化特性，通过分解找到原始信号中的故障点的位置，并且检测出的突变点幅值随着突变点的变化强弱而变化。

图3　不同阈值下的压缩效率与原始数据

图4　采用小波重构处理的加有噪声信号的介损在线监测数据

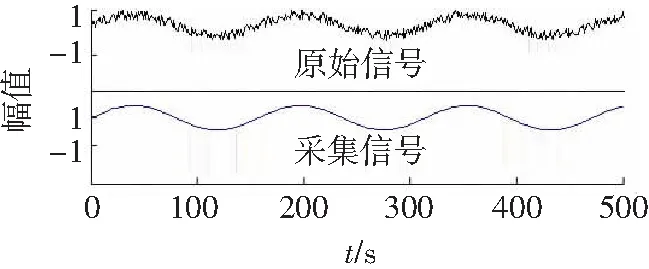
图5　采用最优相关滤波处理带有噪声的介损在线监测数据

图6　原信号与带噪信号的小波变换在小尺度仿真波形

5　结　论

(1)依据嵌入式零树小波包压缩算法，通过选择不同的阈值及压缩比，有效地分离出数据中规律性成分与噪声分量，重构信号与原始信号基本相同。

(2)采用小波变换的方法提取在线监测数据的趋势，不仅能处理非平稳序列，还可以处理宽带噪声在传统数字滤波方法上存在的局限性。

(3)采用最优相关滤波理论与对基波正弦、余弦分量的同步采样方法相结合的方式，能滤除大信噪比下的高次谐波和加性噪声，可以提取不含调制性噪声的基波信号。

[1]沈显庆. 容性设备介质损耗角的分布式测量关键技术的研究[D]. 沈阳： 沈阳工业大学， 2010.

[2]黄晶. 基于小波和改进相关分析的介损值算法研究及其应用[D].长沙： 湖南大学， 2006.

[3]王刘旺. 容性电力设备绝缘监测数据分析与特征提取[D]. 北京： 华北电力大学， 2013.

[4]陈海文. 基于小波去噪结合高阶正弦拟合法的介质损耗角测量技术研究[D]. 镇江： 江苏大学， 2013.

[5]袁飞， 杨震男， 卢毅. 一种基于相对比较法测量容性设备介质损耗的滤波算法[J]. 电力系统保护与控制， 2015， 43(9)： 95-100.

[6]沈显庆. 变电站容性设备介质损耗角的高精度测量方法[J].黑龙江科技大学学报， 2014， 24(1)： 91-94.

[7]王剑. 电容性设备介质损耗角tanδ的监测技术研究[J]. 仪表技术与传感器， 2014(3)： 82-84.

[8]郭松林， 王吉元. 基于小波变换的相关函数介质损耗角测量算法[J]. 黑龙江科技大学学报， 2012， 22(3)： 273-276.

(编辑徐岩)

Research on data compression and pretreatment method of substation capacitive equipment dielectric loss angle on-line monitoring

SHENXianqing,DUANXiaolong

(School of Electrical & Control Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

Dielectric loss angle is an important index reflecting insulation degree of substation capacitive equipment. On-line monitoring and processing method uses the digital measurement technology. This paper proposes an embedded zero tree wavelet algorithm with variable compression ratio designed for overcoming dispersion and redundancy in monitoring data due to aging mechanism of insulation characteristic. This algorithm works by effectively compressing data, improving the efficiency of information management, filtering out false signals such as serrated wave and faulty value using optimal related filter circuit, and transforming the signal to the frequency domain signal, and extracting the eigenvalues by the method of wavelet reconstruction. Both simulation and verification show that the algorithm affords an improved accuracy of capacitive equipment insulation diagnosis.

embedded zerotree wavelet algorithm； optimization correlative filter； wavelet reconstruction； dielectric loss angle； on-line monitoring

2016-02-16

黑龙江省教育厅科学技术研究项目(12541697)

沈显庆(1969-)，男，吉林省通化人，教授，博士，研究方向：电力系统绝缘参数检测与数据处理，E-mail：shenxianqing2001@163.com。

10.3969/j.issn.2095-7262.2016.02.016

TM835.4

2095-7262(2016)02-0187-05

A