电动轮式全向移动机器人行走系统控制算法研究

吴战国，鲁 飞

（同济大学 机械与能源工程学院，上海 200092）

机器人技术

电动轮式全向移动机器人行走系统控制算法研究

吴战国，鲁 飞

（同济大学 机械与能源工程学院，上海 200092）

针对传统的轮式移动机器人在空间狭小、工况复杂的环境下行走困难等问题，设计了一种基于单片机控制的电动轮式全向移动机器人行走系统。结合阿克曼转向原理和电子差速算法对全向机器人进行运动分析，得出不同运动模式下各轮转速与转角的数学模型；利用MATLAB中Simulink模块对模型进行仿真，分析仿真结果并得出结论。为今后全向移动机器人的研究提供一定的参考价值。

全向移动；阿克曼原理；电子差速；控制算法

0　引言

移动式机器人已被广泛应用于高端制造、智能仓储、大型设备维护与检修等领域。为了降低移动机器人的运动空间，提高其运动灵活性与工作效率，全方位移动机器人已成为国内外的研究热点。全方位机器人具有所处平面的前后、左右平移和原地自转全部三个自由度，不仅可以实现不变姿态的任意方向移动，还可以保证实时转向时以最小转弯半径运行。目前实现全向移动主要有全向轮和电动轮两种实现模式，本文主要对电动轮式全向移动机器人行走系统的控制算法进行研究。

1　运动分析

电动轮式全向移动机器人由四个独立轮构成行走机构，每个独立轮由两个电机分别控制驱动和转角，其基本运动模式主要包括直线移动、原地自转和独立转向。

1.1直线移动与原地自转

在工作场地宽广、无障碍物的情况下，全向移动机器人可以通过直线运动保证最高的工作效率，通过原地自转来切换成任意工作姿态。直线行驶与原地自转示意图如图1所示。

图1　直线、自转行驶示意图

直线行驶时只需根据初始位置和目标位置的相对位置确定理想转向角δ，设置初始速度为µ，则四轮的运动参数关系为：

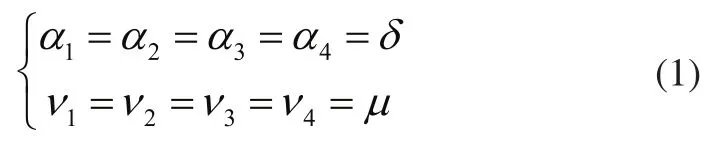
设前后轮距为L，左右轮距为B，原地自转时各轮运动参数关系为：

其中α1，α2，α3，α4及v1，v2，v3，v4分别为轮1，2，3，4的转角与转速。

1.2独立转向运动

多数工况下，移动机器人的工作场地具有一定限制，不能完全通过直行抵达目标点，此时需分析在障碍物的工作环境下各轮转角与转速之间的约束关系，从而提出相应的控制方案和算法。如图2所示为机器人遇障碍物而沿弯曲轨道转向运动示意图。

为了减小轮式机器人转向时路面产生的附加阻力以及降低轮胎的磨损，要求各轮在行驶时满足阿克曼转向原理。

轮式移动常用两种转向模式，一种是传统汽车所采用的前轮转向模式，如图3所示；另一种是四轮协调转向，如图4所示。由文献［3］可知四轮转向相对于前轮转向不仅转向效率高，而且转弯半径小，更符合全向机器人的设计目的。

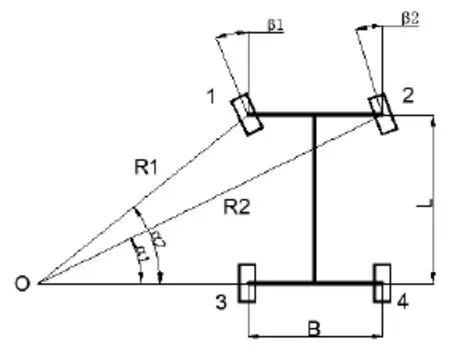
图3　前轮转向运动分析

图4　四轮转向运动分析

为提高机器人运行效率、节省转向空间，本文采用图4所示的四轮协同转向模式。对各轮转速与转角分析得到各参数的数学关系为：

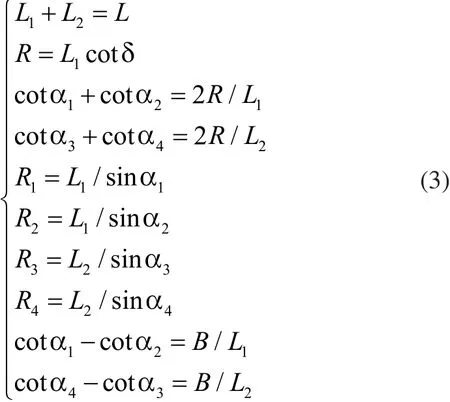
工业搬运机器人运行速度较低，工厂车间中地面状况良好，可假设无质心偏向角，转向中心在前后轮中点的延长线上，即：

整理式（3）和式（4）可以得到转角方程：

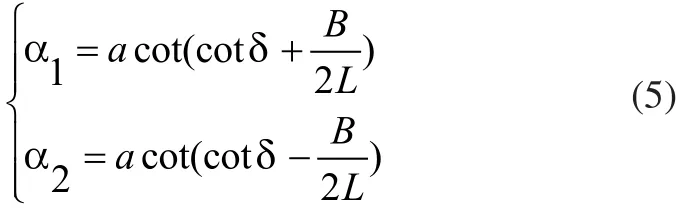
转速方程：

1.3复杂运动数学模型

机器人在复杂工况下可能需要连续转向通过障碍物从而达到运动目标。以图5工况为例，可以通过转向模式与直线运动模式配合，运动路径如图5深色线务a所示，A、B、C、D分别为每段转角的转向中心；也可以通过直线运动合成，运动路径如图5浅色线务b所示。

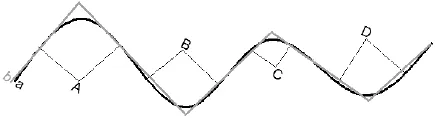
图5　连续转向模式示意图

设δA、δB、δC、δD分别为A、B、C、D四段转角，机器人移动速度为v。

1）曲线a路径的运动模型

依上式类推，可以得到机器人在各阶段的速度和转角值，考虑到矩阵表达的简洁性和运算的便捷性，本文采用矩阵的形式对机器人的运行状态进行描述，不仅更方便对数据进行计算和存储，还易于应对路径变化对控制程序进行调整及扩充。

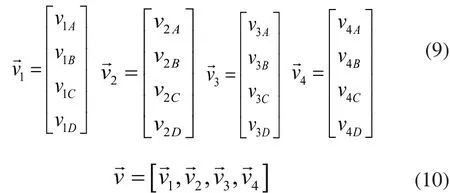
同理可得路径a的转角矩阵为：

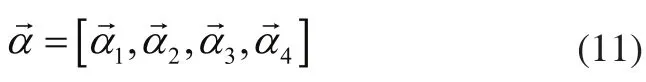
2）曲线b路径的运动模型

由第二章可知各阶段各轮速度为定值：

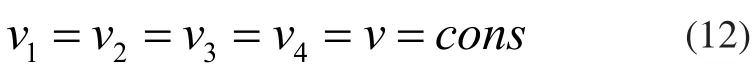
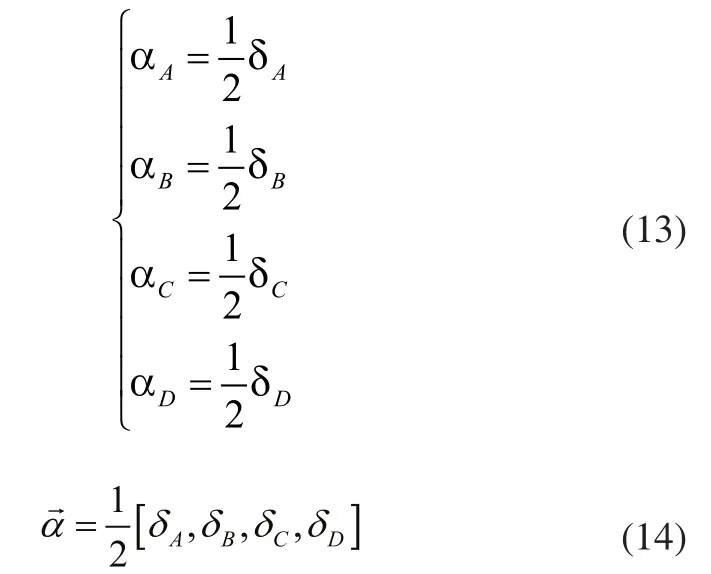
对于a，b两种路径的选择应根据具体工况来制定。一般情况下，连续转向模式（曲线a）运动效率更高，但是对迹规划的准确度和控制精度要求较高。

2　控制系统设计

全向移动机器人的主控制芯片选择为STC80C52单片机，芯片接收上位机发出的转速和转角信号，经过查表后形成控制指令发送给驱动电机与转向电机，由电机控制全向轮运转，此外为提高控制精度和系统稳定性，全向轮的转速与转角由速度编码器和转角传感器反馈给控制单元。闭环控制系统如图6所示。

驱动电机与转向电机的驱动及控制采用L298N控制芯片，转速控制采用现已成熟的PWM电机调速技术。

考虑到普通单片机的计算容量和计算速度难以完成以上算法的精确计算，而选择高性能芯片又将增加成本，所以将机器人的各运动速度与角度生成列表存储。为便于研究，本文预先设定移动机器人模型尺寸基本参数为：L=250mm，B=150mm，取v=0.2m/s，转向角度δ为0°～60°，取值间隔为1°，带入上式计算得到表1所示数值。

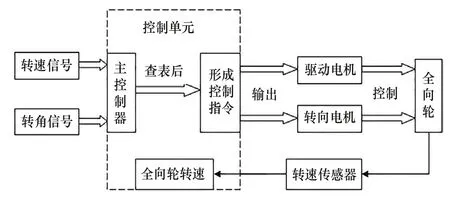
图6　全向移动机器人单轮控制系统图

3　仿真与结果分析

3.1转向系统MATLAB/Simulink仿真模型建立

根据第2节分析，由于直线运动与原地自转模式各参数相关关系明确，不需要进行仿真即可直观得出各轮转速、转角与目的转角关系，所以本章仅对转向运动进行建模仿真，在Simulink中建立模型如图7所示。

表1　转角-速度存储表

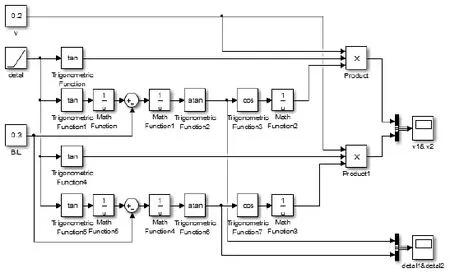
图7 四轮转向系统算法模型

图7所示模型的输出为前轮速度信号v1、v2和转角信号α1、α2分别与输入转向角δ的关系曲线。

3.2四轮转向系统仿真结果分析

搭建图7所示的仿真系统，设定输入转角初始值为0，斜率为0.1rad/s，仿真时长25s（仿真时长25s时便可覆盖机器人从0°～90°的转向模式）。转速与转向角关系的仿真结果如图8所示。

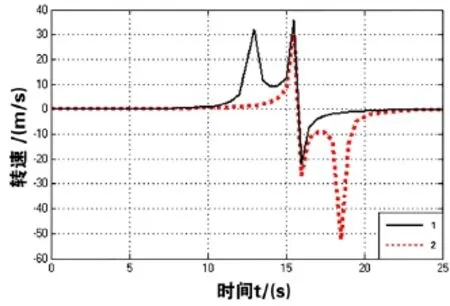
图8　v1-v2仿真结果曲线

【】【】

图8中曲线1和2分别为v1-v2与输入转向角的关系曲线。显然，v1较超前于v2（v1为靠近转向中心一侧电动轮的转速）这与我们传统轮式机械的运动模式相符合；在输入转向角δ为π/2时存在奇点，即当δ接近π/2时，v1和v2趋于无限大；此外，当转角接近π/2.5时，v1也会发生跃变，而当δ大于π/3时，v1与v2偏差较大。显然，当车轮转速处于奇点或两侧轮转速相差较大时，移动机器人的行驶稳定性将受影响，并且不利于各电机的控制与协同。

此外，按上述初始值与仿真时长设置，得到α1-α2与转向角的关系如图9所示。

Design of walking system control algorithm for electric wheeled omnidirectional mobile robot

WU Zhan-guo， LU Fei

TH11

A

1009-0134（2016）10-0088-05

2016-06-06

吴战国（1968 -），男，副教授，博士，主要从事计算机辅助设计和电机控制等研究。