固体火箭发动机装药燃面计算方法
2016-11-03褚佑彪
褚佑彪,张 岗,苑 博,武 渊
(1.中国航天科技集团公司四院四十一所,固体火箭发动机燃烧、热结构与内流场国防科技重点实验室,西安 710025;2.中国航天科技集团公司四院,西安 710025)
固体火箭发动机装药燃面计算方法
褚佑彪1,张岗2,苑博1,武渊1
(1.中国航天科技集团公司四院四十一所,固体火箭发动机燃烧、热结构与内流场国防科技重点实验室,西安710025;2.中国航天科技集团公司四院,西安710025)
通过引入残值函数记录燃面位置,在笛卡尔离散网格上运用惠更斯原理进行燃面显式推移,实现了固体火箭发动机三维复杂药柱的燃面推移模拟和燃面计算功能;采用此算法分别对具有复杂几何构型的药柱和由不同燃速特性的推进剂构成的药柱进行燃面推移模拟。结果表明,此算法精度高、稳定性好,可准确捕捉燃面交汇、分离、消失等复杂拓扑结构变化,适用于复杂装药的燃面计算。
燃面推移;残值函数;笛卡尔离散网格;惠更斯原理
0 引言
燃面计算用于确定装药在燃烧过程中燃烧表面积随燃烧时间的变化规律,直接影响发动机内弹道性能预示精度,是发动机内弹道设计的基础,在固体火箭发动机的设计中一直占有重要地位[1]。传统的燃面计算方法包括解析法、作图法及通用坐标法,均因各自的缺点较明显已鲜有应用。随着计算机相关技术,特别是大型三维工程设计软件的发展,实体造型法应运而生[2-3]。目前,实体造型法主要包括特征造型法和驱动尺寸法。尽管实体造型法在工程中已得到广泛应用,并已成为药型设计的主要手段,但这种基于商用软件的燃面计算程序仍有很大的局限性,比如对于某些特殊几何形状的药型,在CAD软件的推移过程中会出现奇异点,使得燃面推移不能继续下去,只能通过构造近似的几何形状进行燃面计算。
为满足先进固体动力技术的发展要求,药型设计也越来越复杂,对燃面模拟方法不仅提出了适应复杂几何构型的要求,还提出可处理燃面不等速推移的要求,包括处理不同燃速的推进剂在其交界面处同时燃烧的情况,比如单室双推发动机。鉴于实体造型法的局限性,一些新型的燃面计算方法相继出现,其中可实现复杂燃面不等速推移的有网格法[4-5]、Level Set方法[6-7]和最小距离函数法[8-9]等。早期的网格法仅适用于轴对称和二维药柱[3]。2005年,沈伟和邢耀国根据惠更斯原理,构建一种在通用CFD软件非结构网格系统上直接计算燃面推移的数值方法,可以进行三维药柱的燃面分析,但是算法的稳定性有待进一步研究[5]。Level Set方法采用初值形式的偏微分方程将一个纯几何问题转变为用偏微分方程描述的数学问题,但由于在燃面推移过程中需解微分方程组,计算量非常大[6-7,10]。最小距离函数法通过计算药柱内部各点到初始燃面的距离,即最小距离函数(MDF),进行燃面推移分析,可以实现不等速推移[9],但是无法处理不同燃速的推进剂在交界面处同时燃烧的情况。
针对现有燃面模拟方法的不足,本文采用笛卡尔网格离散药柱,通过引入残值函数记录燃面位置,运用惠更斯原理进行燃面显式推移,实现了三维复杂药柱的燃面推移模拟和燃烧面积计算功能。其基本思想是采用笛卡尔网格和残值函数描述当前燃面,通过燃面上球面波影响区域的叠加,模拟燃面的推移过程。此算法的优点是在无需进行网格重构的前提下,自然处理界面拓扑结构变化,准确模拟燃面的推移过程,且计算量较小。
1 实现过程
药柱燃面推移的实现过程简单描述如图1所示。

图1 燃面推移流程图
1.1初始化
为了便于工程应用,同时充分利用CAD软件的强大的实体造型功能,本文首先在CAD软件中建立药柱的几何模型,然后将药柱的面信息(燃面或限燃面)保存为STL格式的文件,文件中记录曲面小三角平面的顶点坐标及其外法向向量。
工程中药柱表面一般为曲面,本文为了降低笛卡尔网格捕捉曲面的数值误差,引入残值函数δi,用于描述真实燃面的几何特征。初始时刻,燃面附近区域采用网格点到初始燃面的最小距离函数作为残值函数,根据网格离散点相对于三角平面的空间位置[9],进行点到面、点到线、点到点3种情况分类计算。
1.2燃面推移
燃面推移模拟的理论基础是惠更斯原理,如图2所示,燃面可以理解为“波阵面”,面上的任一点都可以看作是新的“次波源”,由这些“次波源”发出的“波”所形成的包络面,就是药柱退移到的新燃面,“波”的传播速度对应着推进剂的燃速。由此可知,运用惠更斯原理可实现燃面的不等速推移,燃面推移模拟的一般性原理。
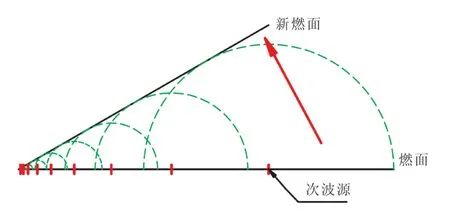
图2 惠更斯传播原理示意图

图3 燃面推移示意图
因此,本文采用惠更斯原理实现燃面的推移,并通过残值函数记录当前燃面的位置,如图3所示。燃面的推移流程可简单描述如下:
第一步:预估燃面上的离散点Pi的影响区域,并向四周推移,在推移的区域内,推进剂转化为燃气,推移位移Δi由式(1)给出。
(1)
式中dt为时间步长;ri为网格点Pi处推进剂的燃速;δi为Pi处的残值函数。
第二步:计算并更新残值函数。如图4所示,Pi为当前燃面上的网格点,Pj为药柱内的网格点且处于Pi的影响范围内。Pj处的残值函数δi由式(2)获得:
(2)
其中,m为当前燃面上能够影响到Pj的网格点数目;εij的值根据Pi与Pj之间是否存在燃速间断进行分类计算:
(1)如图4(a)所示,若Pi与Pj之间没有燃速间断,当Pi与Pj之间的距离dij趋于0时,相应的燃速ri和rj趋于相等,则认为推进剂沿直线燃烧,所以Pj处的εij可由
(3)
获得。
(2)如图4(b)所示,若Pi与Pj之间存在燃速间断,类比折射定律可知,推进剂燃烧路径满足:
(4)
式中θi和θj分别为2种推进剂燃烧路径与推进剂交界面法向量的夹角;O点为推进剂燃烧路径与交界面的交点。
所以,Pj处的εij可由式(5)获得:
(5)
式中dio为Pi到O点的直线距离;doj为O到Pj点的直线距离。
第三步:确定新的燃面,即更新后的燃气区域与药柱区域的交界面。

(a)无燃速间断 (b)有燃速间断
1.3燃面计算
积分获得当前时间步每种推进剂的燃气体积增量。当前时间步内每种推进剂的平均燃面值为其燃气体积增量与推进距离之商。当单一推进剂的推进距离具有空间不均匀性时,可采用平均距离代替,这是因为,用于内弹道预示的物理量是燃气的体积增量[1],即燃面与推进距离的乘积,而不是单一的燃面或推进距离。
1.4内弹道计算,确定燃速
由上述燃面计算过程及内弹道学基本方程可知,在给定燃速ri的情况下,可获得对应的燃面,进而获得对应的燃烧室压强p。而在已知p的前提下,ri可由p直接确定,两者之间一般满足:
(6)
式中ai和ni分别为Pi点处推进剂的燃速系数ai和燃速的压强指数ni。
根据推进剂燃速ri与燃烧室压强p的这两种关系,在数值求解过程中,可在推进剂的燃速ri与燃烧室压强p之间建立循环,直至压强的残差小于设定的预示误差pres,即认为燃烧室内压强的求解过程完成。当前时间步内的燃速由式(6)确定,并可作为下一时间步内燃速的预估值。
2 算例
2.1具有复杂几何构型的药柱
为验证上述算法的正确性,本节选取图5所示具有复杂几何构型的φ400 mm药柱作为验证算例。图6给出计算获得的燃面的变化过程,并与基于Pro/E平台的驱动尺寸方法[2]的结果进行对比。采用主频为2.9 GHz 的计算机进行单线程计算,计算结果如表1所示。基于网格1和网格2的计算机耗时分别为27 s和96 s,误差分别不超过1.2%和0.5%。由此可知,此算法精度较高,计算量较小,满足工程实际应用。

图5 三维药柱结构图

表1 不同计算网格的计算结果对比
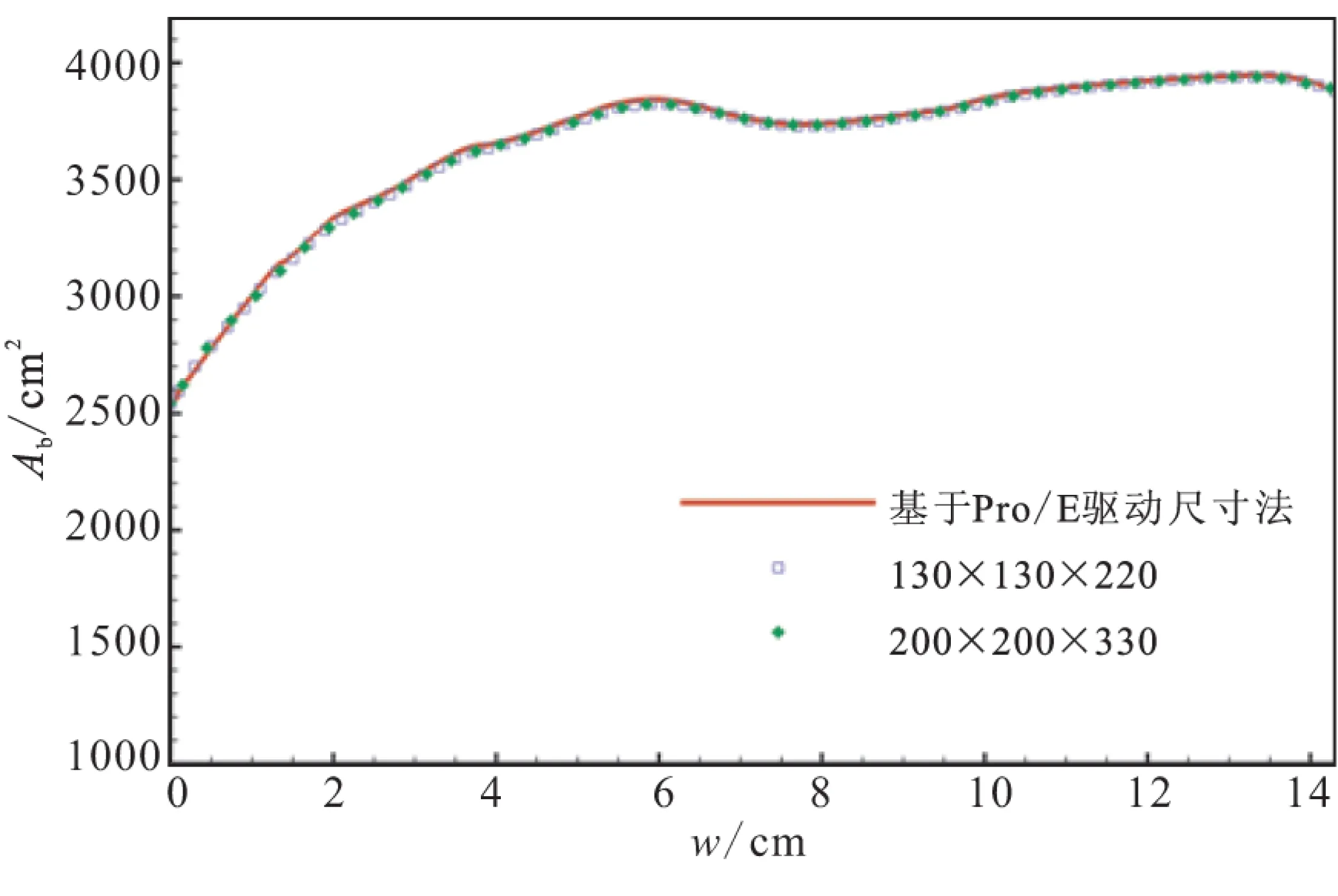
图6 燃烧面积随时间的变化规律
2.2具有不同燃速特性的推进剂构成的药柱
在单室双推发动机的设计过程中,为保证助推段与续航段的推力比,常采用高低燃速搭配的思路进行
助推段和续航段装药设计。当燃面与高低燃速推进剂交界面相交时,推进剂的燃烧速度在燃面上出现强间断,呈现明显的差异性,是燃面退移计算的一个难点。
如图7所示,本节以内孔燃烧药柱作为数值验证算例,图中给出不同时刻药柱过轴的剖面图,灰色区域为高燃速推进剂,黑色区域为低燃速推进剂,白色区域为燃气填充区域。为充分验证当前算法准确处理燃面上存在燃速间断工况的能力,模拟了3个药柱的燃面推移过程,其交界面分别与初始燃面成45°、90°和135°夹角。
由图7可知,在交界面处,药柱几何特征的演化过程均被准确捕捉。验证结果表明,当前算法可准确捕捉由于燃速间断的存在导致燃面的交汇、分离、消失等复杂拓扑结构变化,适用于复杂装药的燃面计算。
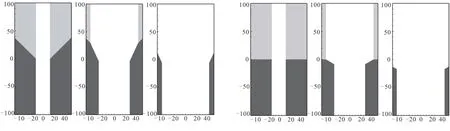
(a)推进剂交界面与初始燃面成45°夹角 (b)推进剂交界面与初始燃面成90°夹角

(c)推进剂交界面与初始燃面成135°夹角
3 结论
(1)此算法基于燃面推移的一般性原理——惠更斯原理,不仅可处理燃面的等速推移,还可处理燃面的不等速推移,包括燃面上存在燃速间断的工况。
(2)采用笛卡尔网格离散药柱,对当前燃面的影响区域可有效地提前预估,将三维体循环缩减为具有一定厚度的曲面循环,大大降低了计算量。
(3)残值函数的引入,不仅有效地控制燃面推移的累计误差,准确计算燃面,还可自然处理界面拓扑结构变化,避免燃面的网格重构,提高算法的稳定性。
[1]陈汝训,刘铭初,李志明.固体火箭发动机设计与研究(上)[M].北京:中国宇航出版社,1991.
[2]董新刚,陈林泉,侯晓.基于Pro/E平台下的固发装药CAD软件[C]//2002年中国宇航学会固体推进专业委员会年会论文集(上),昆明:2002:109-114.[3]于胜春,赵汝岩,周红梅,等.基于Pro/E特征造型技术的固体发动机装药燃面计算[J].固体火箭技术,2005,28(2):108-111.
[4]Hejl R J,Heister S D.Solid rocket motor grain burnback analysis using adaptive grids[J].Journal of Propulsion and Power,1995,11(5):1006-1011.
[5]沈伟,邢耀国.基于非结构网格的燃面推进算法[J].固体火箭技术,2005,28(3):176-179.
[6]Sethian J A.Theory,algorithms,and applications of level set methods for propagating interfaces[J].Acta Numerica,1995,5(5):309-395.
[7]秦飞.固体火箭发动机复杂装药燃面算法研究[D].西安:西北工业大学,2003.
[8]Willcox M A,Brewster M Q,Tang K C,et al.Solid propellant grain design and burnback simulation using a minimum distance function[J].Journal of Propulsion Power,2007,23(2):465-475.
[9]马长礼.固体火箭发动机MDF燃面计算方法研究[D].长沙:国防科学技术大学,2007.
[10]费阳,胡凡,张为华,等.基于平行层推移的含表观裂纹缺陷固体发动机装药燃面计算[J].固体火箭技术,2011,34(4):466-469.
(编辑:吕耀辉)
Burning surface computing method for solid rocket motor grain
CHU You-biao1,ZHANG Gang2,YUAN Bo1,WU Yuan1
(1.The National Key Laboratory of Combustion,Thermostructure and Flow of SRM,The 41st Institute of the Fourth Academy of CASC,Xi'an710025,China;2.The Fourth Academy of CASC,Xi'an710025,China)
A new computational method, based on a Cartesian grid and Huygens' principle of wave propagation,is presented for simulating the evolution of the burning surface regression of a complex,three-dimensional solid rocket motor propellant grain.The residual displacement function (RDF) is introduced to describe the location of complex burning surface on the Cartesian grid.Burning surface calculation of grain with complicated geometry or multi-burning rate was performed.The results indicate that the method has high precision and good stability,and it is capable of dealing with complicated structure changes such as burning surface intersection,separation and vanishing.It is demonstrated that the method provides a new technical measure for burning surface calculation of complicated propellant grain.
burning surface regression;residual displacement function;Cartesian grid;Huygens' principle of wave propagation
2015-08-31;
2015-11-05。
褚佑彪(1987—),男,博士,研究方向为固体火箭发动机设计。E-mail:cyber@mail.ustc.edu.cn
V435
A
1006-2793(2016)04-0488-04
10.7673/j.issn.1006-2793.2016.04.007
