涡脱落撞击潜入式喷管引起低频压力振荡研究
2016-11-03杨羽卓
杨羽卓,郜 冶
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
涡脱落撞击潜入式喷管引起低频压力振荡研究
杨羽卓,郜冶
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨150001)
通过不同障碍高和不同加质的冷流数值模拟,着重研究碰撞频率(碰撞处压力振荡频率)与强度(碰撞处prms/pmean)对于SRM内压力振荡幅频特性的作用程度。研究结果表明,SRM内压力振荡幅度与碰撞处的压力振荡大小为相同量级。当碰撞强度较小时,碰撞只起到增强声场的作用;当碰撞强度较大时,碰撞产生的压力振荡随碰撞强度的增加逐渐覆盖淹没声场。SRM内压力振荡的幅频特性主要由涡脱落碰撞强度决定,一般只呈现低频且具有非声非线性特征。
不稳定燃烧;涡脱落;压力振荡
0 引言
阿丽亚娜5号发动机发生燃烧不稳定问题之后,大量的研究分析了这一现象发生的原因。Flandro和Jacobs[1]首先提出涡声耦合可能是导致发动机不稳定燃烧的一个因素。Culick和Magiawala[2]及Dunlap和Brown[3]的实验表明,如果燃烧室中涡脱落频率与声频耦合,将带来压力振荡。Anthoine团队开展了一系列的理论[4]、实验[5]和数值研究[4],发现当绝热环引起的障碍涡脱落与潜入式喷管入口处发生碰撞时,就会产生压力振荡,且振荡的幅值随着潜入式喷管空腔体积的增大而增大。此外,基于Titab 34D和阿丽亚娜5号的结构,Brown[6]、Flatau和Moorhem[7]等设计了一系列冷流实验,得到相似结论。这些研究中,都指出障碍处周期性脱落的涡在下游喷管入口处发生碰撞时,会产生反馈声信号,这个反馈声信号又放大涡的振荡,并将其频率调整成对应的声模态。这个作用过程表明,涡声耦合是导致压力振荡的根本原因,而涡在下游的碰撞则是发生涡声耦合的前提。然而,SRM中涡声耦合导致严重压力振荡的结论依然存在很大争议。首先,Flandro[8]指出,只有当下游的碰撞面与剪切层起点有合适的距离,且碰撞面需要有合适的角度时,反馈声波才能放大剪切层不稳定引起的压力振荡。因此,接收点处的声信号与周期性的涡脱落应具有一致的频率与相位。然而,考虑到发动机内流动复杂(伴有多种阻尼因素),发生耦合的概率是很小的。其次,已有的针对大长径比发动机的实验[9-10]都表明,发生涡声耦合时,低频压力振荡的幅值没有超过0.5%。另外,如果压力振荡源自涡声耦合,则耦合和非耦合状态下的涡所具有的能量和尺寸应存在较大差异(剪切层邻近区域的小扰动被空间放大,并激发大尺寸涡街结构[1])。然而,Anthoine[11]的实验表明,马赫数相同时,耦合(压力振荡0.12%)与非耦合(压力振荡0.006%)状态下的涡所具有的物理特性变化很小(能量增大8%,尺寸增大9%),这些小幅度的波动无法解释压力振荡的巨大变化。考虑到实验中的非耦合状态是通过扰乱耦合状态的涡脱落频率实现的,Anthoine推测较大的压力振荡应源自涡在下游周期性碰撞,但并没有进一步验证这一推测。此外,北京理工大学的发动机涡声耦合实验得出[12],平均马赫数对压力振幅的影响显著;在涡声耦合敏感马赫数区间内,当涡脱落频率十分接近声频时,压力振幅最大,但随着马赫数的继续增大(涡撞击强度增大),压力振幅也继续增大,且超过涡声耦合时的振幅。
本文认为涡声耦合产生的有限幅度压力增大,只是碰撞强度(prms/pmean)小时发生的一种共振现象;发动机内产生较大压力振荡的原因是周期性涡脱落在下游发生大强度碰撞。所以,研究脱落的涡与喷管入口处不同强度与频率的碰撞对发动机内流场压力的影响程度是很有必要的。
1 计算方法与模型
1.1计算方法
本文使用CFD软件FLUENT分别模拟不同径向加质和不同障碍高度情况下燃烧室内不同位置的压力振荡特性,不同加质和障碍高度会带来的不同涡脱落频率和不同碰撞强度与频率。用碰撞处压力振荡与平均压力比值的大小代表碰撞强度,研究碰撞的幅频对燃烧室内压力振荡的影响。采用LES方法,保证y+<1,计算结果已与冷流实验值对比,保证结果可靠性[13]。
1.2计算模型
为了便于与冷流实验对照,计算模型采用阿丽亚娜5缩比模型[4],此模型具有潜入式喷管空腔体积较大,且绝热环距离喷管入口较近的特点,易于发生涡声共振耦合情况。采用侧向加质边界条件,流体为常温(与冷流实验一致)。通过改变加质来调节初始速度,通过改变障碍(绝热环)高度来调节涡脱落频率和涡传播速度[11],得到接近于不同声频的涡脱落以及涡在喷管入口处不同强度的碰撞。加质2、4、0.1 kg/(s·m2),障碍高度分别为9、5、2、1 mm。燃烧室头部为壁面,几何模型和压力监测点位置见图1。
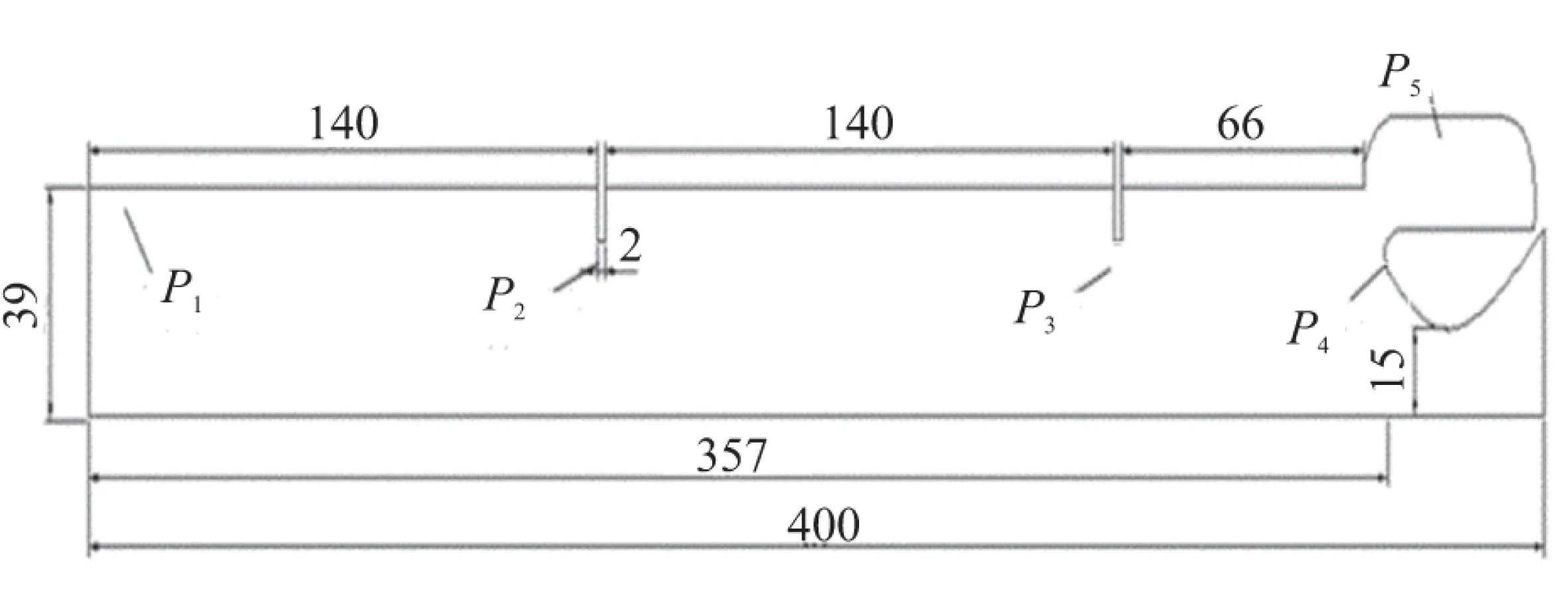
图1 计算模型及压力采集点位置
2 小强度碰撞引发涡声耦合作用与较大强度碰撞扰乱涡声耦合作用
2.1SRM中的声波
发动机头部封闭,喷管喉部直径较小,即喷喉声阻尼较小,发动机近似为两端封闭的圆柱形腔体,声在其中的传播主要是一维纵向驻波。涡在下游与喷管反应产生声波,波传播又在燃烧室头部反射,这个反射波与之前的瞬时波干涉形成驻波。发动机近似圆管相当于一个共振器[14],它有其固有声频,各阶固有声频计算式为
fa=nc/2L
(1)
式中fa为声频;n为声模态阶数;c为声速;L为燃烧室长度。
针对本文模型,发动机前4阶固有声频计算结果见表1。

表1 各阶固有声频
当涡的脱落频率与固有声频相近时,会发生涡声耦合,涡脱落频率在各阶声频之间跳动,而涡与喷管入口处的碰撞又将声压级提高到共振条件,并将能量以某一阶声模态反馈到剪切层,将涡脱落频率调整到对应的声频,并放大压力振荡。
2.2SRM中涡脱落特性
燃烧室中的障碍,如绝热环等,会产生高度剪切流,并产生持续的周期性的涡脱落。在自由区域中,障碍涡脱落频率与来流速度和障碍尺度之间的关系可用Str数来联系,在自由流场圆柱绕流中,Re为200~30 000之间,Str可取为0.2[1],但在本文所研究的SRM有限制的区域中,声模态会对涡脱落产生影响,当涡脱落频率在能够发生涡声耦合的区间内时,受声场的影响,涡脱落频率会从某一阶声频跳到另一阶。已有PIV实验[11]得出,发生涡声耦合时,涡脱落处的频率与速度对应的点分布在一条直线上,这条直线即Str恒为2.45。所以,可通过计算Str数值,判断是否发生涡声耦合。
Str计算式为
(2)
式中f为涡脱落频率;l为障碍涡脱落到喷管入口碰撞位置的轴向距离;U0为涡脱落处的平均轴向速度。
障碍涡脱落后逐渐衰减耗散,并在下游潜入式喷管入口处发生碰撞,见图2。周期性的碰撞产生压力振荡,碰撞强度取决于涡的强度。

(a) 涡传播 (b) 涡碰撞前 (c) 涡碰撞
2.3SRM中小强度与较大强度碰撞现象数值模拟
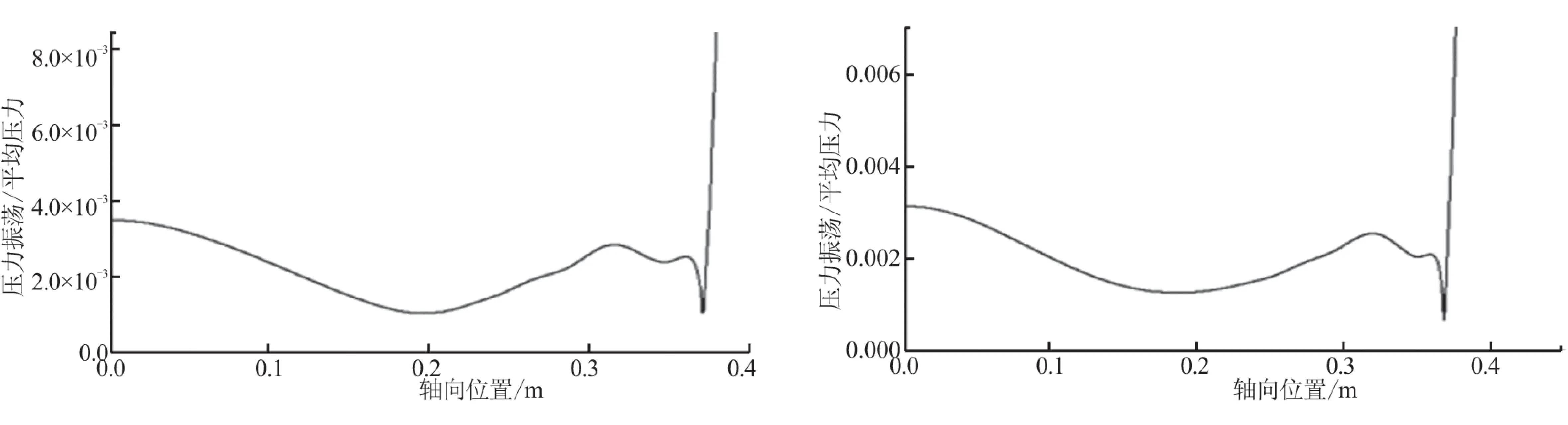
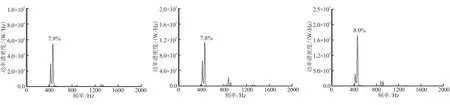
计算侧向加质条件,加质2 kg/(s·m2)。障碍高度分别为9、5、2、1 mm。几何模型和压力监测点位置已在图1中给出。图3为不同障碍高涡量图。可看出,相同加质时,涡的强度随障碍高度而增大。涡脱落后,在下游喷管入口处发生碰撞,涡的强度越大,碰撞作用必然也越强。图4为不同障碍高度各监测点压力振荡频率。图5为不同障碍高对称轴附近压力振荡与平均压力的比值随轴向位置的变化图。图6为压力振荡与平均压力比值云图,并画出了对应的声振型。

(a) 障碍高1 mm (b) 障碍高2 mm

(c) 障碍高5 mm (d) 障碍高9 mm
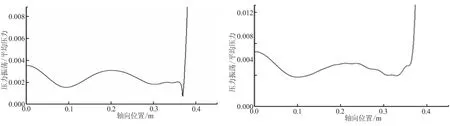
从图4~图6中得出,障碍高1、2、5 mm时,发生了清晰的涡声耦合。以2 mm障碍高为例,图4(b)中燃烧室各特征点压力振荡发生了清晰的一阶声频共振,图5(b)中体现了清晰的一阶声振型,燃烧室两端为压力振荡,波腹中间为压力振荡波节,图6(b)中的压力振荡与平均压力的比值云图也呈现了对应的声振型特征。与2 mm障碍的结果类似,5 mm障碍高发生了二阶声频共振,各点压力振荡频率、压力振荡波形和云图都体现了二阶声频共振的特征。9 mm障碍模拟结果与其他3种障碍高度结果略有不同,不是明显的涡声耦合状态。从图4(d)中发现,障碍9 mm高的情况,虽然压力振荡也在各阶声频附近,但没有发生清晰的单一频率共振,图5(d)和图6(d)中压力振荡波形虽然近似二阶共振,但在后半段出现了波动。表2中,对比了不同障碍高情况的头部点与碰撞处的压力振荡频率与幅值,发现9 mm障碍高情况碰撞强度较大,且碰撞频率不等于声频。所以,9 mm障碍情况发生不清晰的涡声耦合状态,是由于涡较大强度的碰撞影响了燃烧室内的声场,扰乱了涡声耦合作用。
计算不同障碍高情况模拟结果Str值,并与理论值[11]比较,见图7。由于对涡脱落在下游碰撞起主要作用的是距离喷管入口处的障碍,所以平均轴向速度和涡脱落频率给出的是此障碍处的数值,见表3。图7中,得出障碍高1、2、5 mm时,涡脱落频率与平均速度很好地满足理论值,但障碍高9 mm时,模拟结果却偏离理论值。这个结果进一步证明,9 mm情况有较大强度碰撞,扰乱涡声耦合状态。
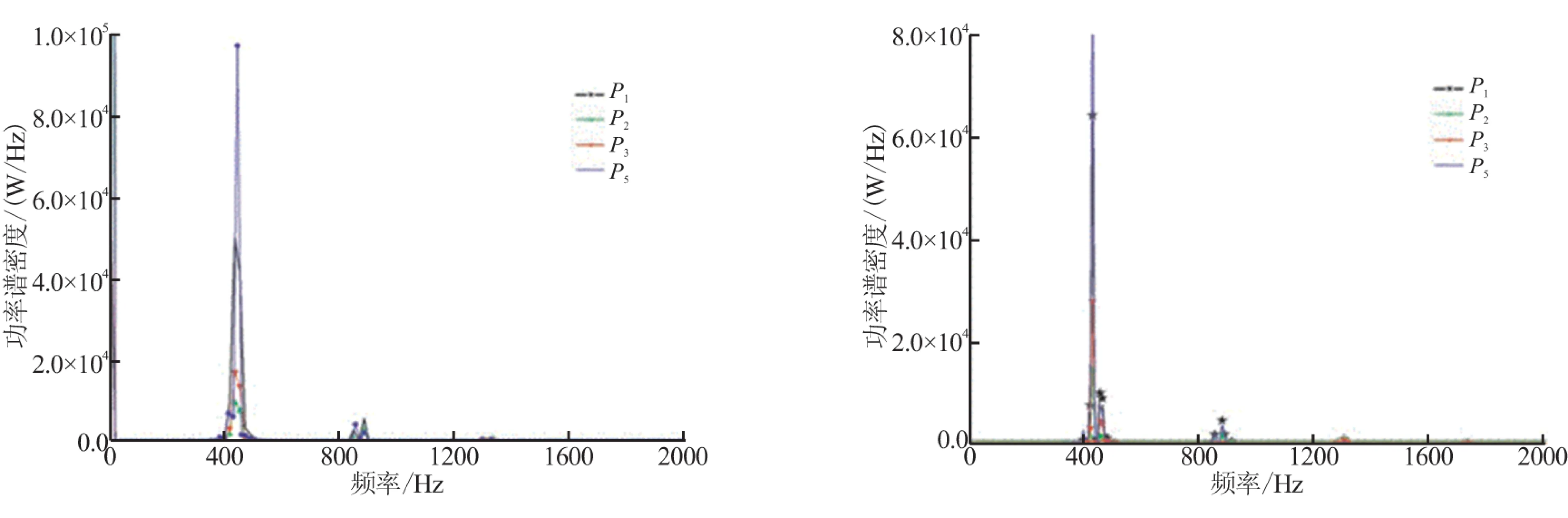
(a) 障碍高1 mm (b) 障碍高2 mm
(c) 障碍高5 mm (d) 障碍高9 mm
(a) 障碍高1 mm (b) 障碍高2 mm
(c) 障碍高5 mm (d) 障碍高9 mm

(a) 障碍高1 mm (b) 障碍高2 mm

(c) 障碍高5 mm (d) 障碍高9 mm
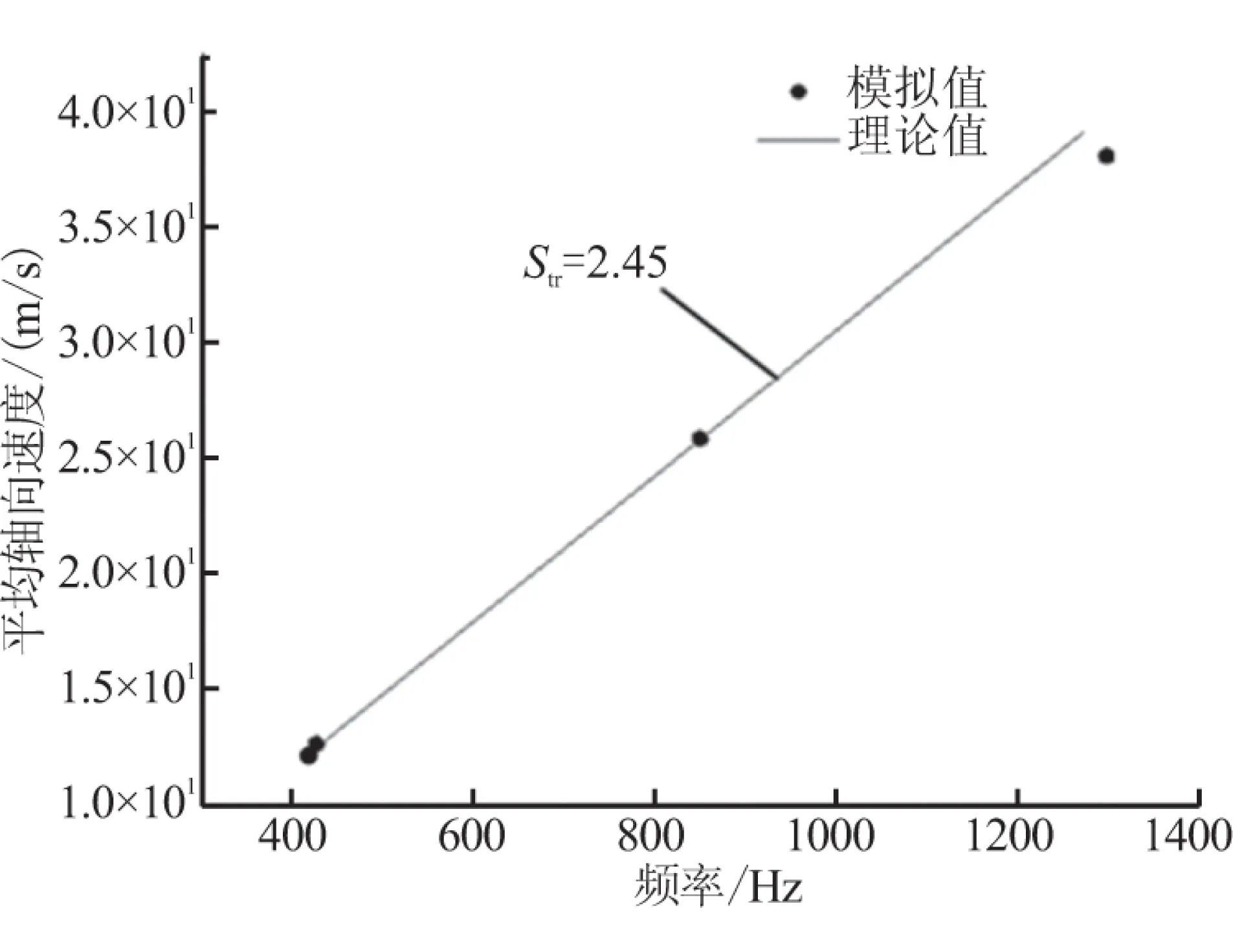
图7 涡脱落频率与流速和Str数的关系
头部和碰撞处压力振荡的频率与幅值见表2,从表2得出,不同障碍高情况下头部压力振荡总是与碰撞处压力振荡在同一量级,且障碍高9 mm时,压力振荡并不比1、2、5 mm这种发生清晰涡声耦合的情况小。所以,合理推测是碰撞处压力振荡对燃烧室内的流动起到了明显作用。1、2、5 mm情况,由于碰撞处的强度低,即便碰撞频率略微偏离声频,声场也会通过调节涡脱落频率,使得燃烧室在声频共振,发生涡声耦合。障碍高9 mm情况,碰撞强度较大,碰撞处的作用已经逐渐淹没声场。
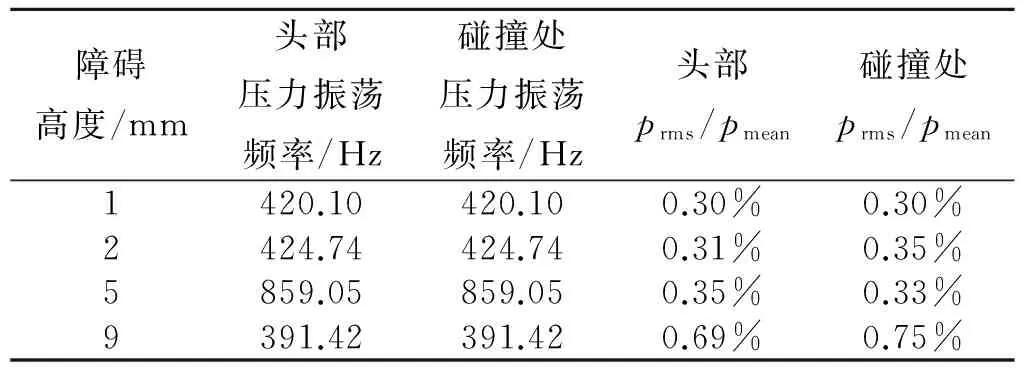
表2 头部与碰撞处压力振荡的频率与幅值
不同障碍高度涡脱落处速度与频率见表3。表3中,给出此时涡脱落频率为1 307 Hz,接近三阶声频,但头部的压力振荡频率完全与碰撞处一致(391.42 Hz),说明较大强度碰撞会扰乱涡声耦合作用,引起低频高幅值压力振荡。
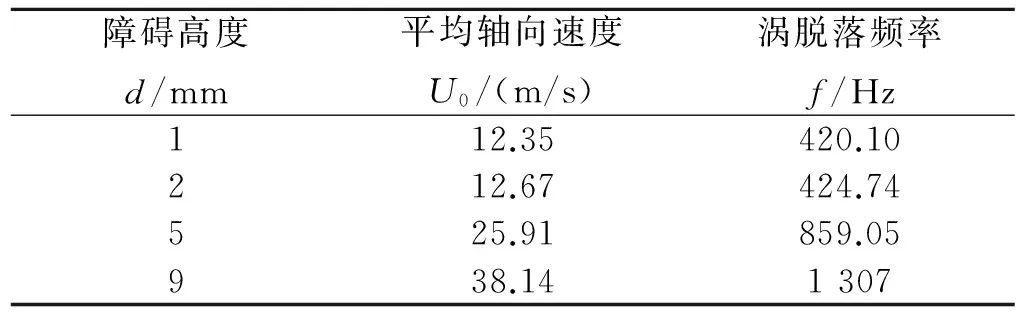
表3 不同障碍高度涡脱落处速度与频率
3 大强度碰撞前提下由涡脱落碰撞主导的燃烧室内压力振荡幅频特性
当涡脱落后,在下游碰撞强度较大时,碰撞处压力振荡的频率与幅值特性将主导燃烧室内的流动。由于本文只是2D的数值模拟结果,会放大压力振荡的作用,真实热环境的发动机中,有各种对振荡的抑制因素存在,并不会出现文中这么大量级的压力振荡,但这并不妨碍接下来模拟结果对于涡脱落碰撞作用的研究。至少可看到二维轴对称药型涡脱落可达到的最大影响程度。
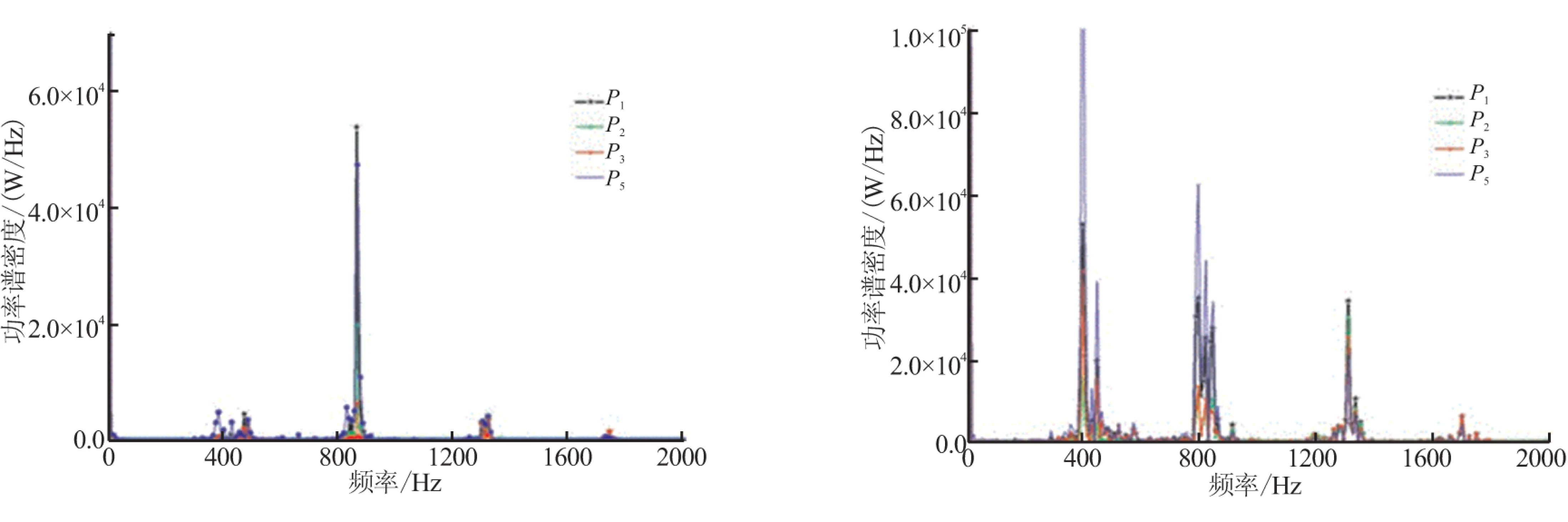
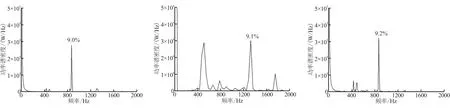
计算模型仍采用图1的结构,压力采集点位置也与图1相同。计算侧向加质4 kg/(s·m2)时障碍高度2、5、9 mm情况,采集燃烧室头部、涡脱落处和碰撞处的压力振荡频率与幅值(prms/pmean表示在功能谱密度峰值上方),图8、图9给出了障碍高2、5 mm结果。发现头部压力振荡与碰撞频率一致,且燃烧室各点压力振荡量级与碰撞处相同。图8(c)中,最主要的振荡频率为450 Hz,次主要频率为416 Hz,图8(a)和图8(b)中,虽然416 Hz振荡频率的也很明显,但仍以450 Hz为主频率。图9(b)中看出,涡脱落频率为465 Hz和1 320 Hz,但图9(a)头部压力振荡频率却与图9(c)中碰撞处一致,都为865 Hz,接近固有声频的涡脱落,并没能引起涡声耦合,碰撞处的作用更明显。障碍高9 mm情况,得到相同规律。
图10和图11为压力振荡与平均压力比值沿轴向位置变化,得出燃烧室内不再体现声振型特征,说明此时已经没有涡声耦合作用,但压力振荡却比图5中涡声耦合情况要剧烈,这就是大强度碰撞所导致的。图8、图9中,虽然压力振荡主频也在各阶声频附近,但并没有观察到声振型,且图9中涡脱落也有其独立频率,说明涡脱落碰撞产生的压力扰动作用已经覆盖淹没了小幅度压力振荡的声场。
(a) 燃烧室头部 (b) 第2个障碍涡脱落点 (c) 喷管入口处碰撞点
(a) 燃烧室头部 (b) 第2个障碍涡脱落点 (c) 喷管入口处碰撞点
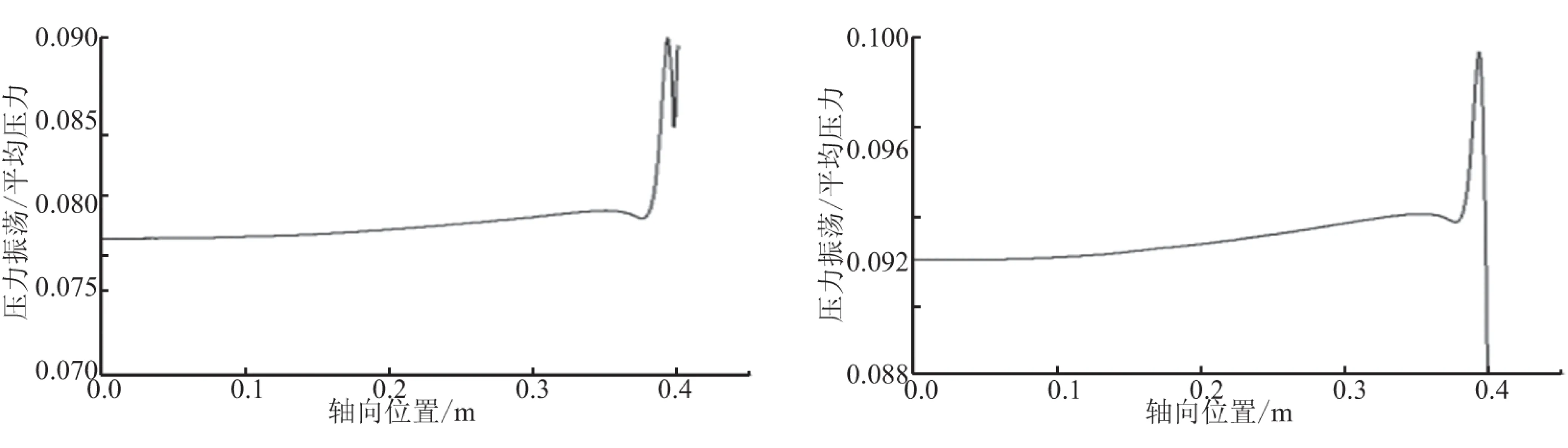
(a) 障碍高2 mm (b) 障碍高5 mm

(a) 障碍高2 mm (b) 障碍高5 mm
图12为侧向加质0.01 kg/(s·m2)障碍高9 mm情况的模拟结果,此时碰撞强度很大(80%),可更充分地验证涡脱落碰撞的幅频特性对于调节流场的作用。燃烧室内发生120 Hz共振,远小于固有声频,且无声振型,压力振荡却高达平均压力80%。此种情况只是二维简化模型模拟的单纯流动问题,压力振荡如此高是由于加质量小燃烧室内平均压力低,虽然偏离实际,但不影响研究涡脱落碰撞作用。燃烧室内存在大强度涡脱落碰撞时,燃烧室内压力振荡的幅频特性总是与碰撞处一致,呈现典型的非声非线性特征。
此外,已有研究中[4]有结果显示,潜入式喷管空腔体积越大,压力振荡越大,而没有空腔时,压力振荡非常小。图13分别给出了有潜入式喷管和无潜入式喷管的平均流场流线图。图13(a)中,流线图能观察到障碍后回流区与喷管入口处有一定距离,且碰撞作用使得喷管入口处碰撞位置前又形成了涡;当没有空腔时,回流区紧贴喷管入口处。这也说明了碰撞的重要作用。
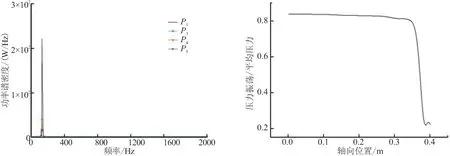
(a) 各点压力振荡频率 (b) 压力振荡沿轴向位置变化
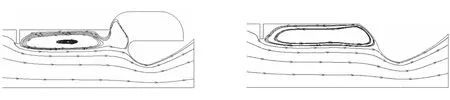
(a) 有潜入式喷管流线图 (b) 无潜入式喷管流线图
4 结论
(1)碰撞强度较小(低于0.5%)时,碰撞带来的压力振荡贡献给了流场的扰动,当碰撞频率与燃烧室固有某一阶声频恰好一致时,碰撞带来的压力振荡反馈通过增强声场来放大燃烧室内的压力振荡,发生涡声耦合。燃烧室内压力振荡频率为声频,并呈现出对应的声振型。但压力振荡幅值与平均压力的比值并不大。
(2)碰撞强度较大(高于8%)时,碰撞处压力振荡的频率与幅值决定了燃烧室内压力振荡的幅频特性。燃烧室内压力振荡大小与碰撞处一致,即便碰撞频率接近某一阶声频,燃烧室内压力振荡也不再体现声振型,压力振荡呈现非声非线性特征。此时,碰撞的压力振荡反馈已经覆盖淹没了声场,声场的作用被忽略,涡脱落的频率和强度独立发挥作用。此时,压力振荡远大于上述涡声耦合时的压力振荡幅值。
(3)碰撞强度略大,但还不足以覆盖声场的作用时(0.75%),碰撞处压力振荡的幅频特性会影响声场,当碰撞频率与声频有差距时,声场压力振幅仍被加强,但声振型被扰乱。
[1]Flandro G A, Jacobs H R. Vortex-generated sound in cavities[C]//Aero-acoustics Conference, Washington, 1973: 15-17.
[2]Culick F E C, Magiawala K. Excitation of acoustic modes in a chamber by vortex shedding[J]. Sound Vib, 1979, 64(3): 455-457.
[3]Dunlap R, Brown R S. Exploratory experiments on acoustic oscillations driven by periodic vortex shedding[J]. AIAA, 1981, 19(3):408-409.[4]Anthoine J, Buchlin J M, Hirschberg A. Effect of nozzle cavity on resonance in large SRM theoretical modeling[J]. Propul Power, 2002, 18(2): 304-311.
[5]Anthoine J, Lema M R. Passive control of pressure oscillations in solid rocket motors cold-flow experiments[J]. Propul Power, 2009, 25(3): 792-800.
[6]Brown R S, Dunlap R, Young S W. Vortex shedding as a source of acoustic energy in segmented solid rockets[J]. Spacecraft Rockets, 1981, 18(4): 312-319.
[7]Flatau A, Van Moorhem W. Prediction of vortex shedding responses in segmented solid rocket motors[C]//26th Joint Propulsion Conference and Exhibit, Florida, 1990: 16-18.
[8]Flandro G A. Vortex driving mechanism in oscillatory rocket flows[J]. Journal of Propulsion, 1985, 2(3): 206-214.
[9]Prahalad N Tengli. Vortex flow analysis of a large segmented solid rocket motor[J]. India Journal of Science and Technology, 2012, 5(1): 1888-1892.
[10]Yves Fabignon.Instabilities and pressure oscillations in solid rocket motors[J]. Aerospace Science and Technology, 2003, 7(3): 191-200.
[11]Anthoine J.Experimental and numerical study of aeroacoustic phenomena in large solid propellant boosters[D]. Von Karman Institute, 2000.
[12]张峤,李军伟,王伟臣, 等. 固体火箭发动机涡声耦合特性数值研究[J]. 推进技术, 2011, 32(3): 348-354.
[13]杨羽卓,郜冶. 燃烧室障碍涡与声腔共振耦合的条件与影响因素[C]//榆林:固体火箭推进专业第三十一届年会,2014.
[14]Viviana F. Numerical simulations of acoustic resonance of solid rocket motor[D]. University of Rome, 2011.
(编辑:崔贤彬)
Study on low frequency pressure oscillations induced by vortex impacting on submerged nozzle
YANG Yu-zhuo,GAO Ye
(Harbin Engineering University,Department of Aerospace Engineering,Harbin150001, China)
Cold flow numerical simulation of different obstacle's height and different mass flow injection was developed to study the effect of vortex impact frequency and intensity on pressure oscillations magnitude-frequency characteristic in chamber. The results show that the pressure oscillation amplitude in chamber and at the location of impact has the same order of magnitude. The impacts only strengthen acoustic field when the impact strength is not strong, but with the increase of impact strength, the pressure oscillation induced by impact gradually covers acoustic field. The pressure oscillations magnitude-frequency characteristic in chamber is mainly decided by the frequency and strength of vortex impacting, which usually presents low frequency, nonlinear and non-acoustic.
unsteady combustion;vortex shedding;pressure oscillation
2015-06-18;
2015-08-22。
国家自然科学基金(11372079)。
杨羽卓(1991—),女,硕士生,研究方向为发动机燃烧稳定性。E-mail:13903614581@163.com
V435
A
1006-2793(2016)04-0456-07
10.7673/j.issn.1006-2793.2016.04.002
