电动汽车动力系统参数多指标稳健设计方法

于丽敏　熊会元,2　宗志坚,2　吴义忠

1.中山大学，广州，510006　2.东莞中山大学研究院，东莞，523808 3.华中科技大学，武汉，430074



电动汽车动力系统参数多指标稳健设计方法

于丽敏1熊会元1,2宗志坚1,2吴义忠3

1.中山大学，广州，5100062.东莞中山大学研究院，东莞，523808 3.华中科技大学，武汉，430074

为降低行驶工况的波动对整车经济性能的影响，提出基于多因素行驶工况的动力系统部件参数多指标稳健设计方法。以工况能耗、工况续驶里程和部件成本建立综合经济性能指标函数，以电池、电机和传动系参数为控制因子，以行驶工况的关键因素作为噪声因子，建立动力系统参数稳健设计的数学模型。基于Modelica建立整车性能仿真模型，并构建工况仿真的径向基函数响应面模型。采用概率方法描述行驶工况的不确定性，制订试验设计方案对动力系统参数进行稳健设计。以EVBus进行实例计算，基于蒙特卡罗分析表明稳健设计方案的综合性能指标函数的均值及方差均得到有效改善，表明了研究方法的有效性。

电动汽车; 稳健设计; 行驶工况；径向基函数

0　引言

纯电动汽车的动力系统主要由电池、电机和传动系构成，动力系统各部件的合理匹配和参数优化是整车开发中的关键问题。在相同的动力系统配置和控制策略下，不同的行驶工况对整车性能有很大的影响[1]。动力系统参数的优化方法中通常以循环工况[2-4]或数个循环工况的组合[5-6]为运行条件进行确定性优化设计，仅考虑速度的变化对整车经济性能的影响。而实际工况中的载荷、路面条件、道路坡度、风速等运行条件不是固定不变的，即具有不确定性。以典型工况为运行条件的传统动力系统部件参数优化设计方法，忽略了不确定性的行驶工况对整车能耗的影响，其整车经济性在实际运行环境下将达不到预期效果。

稳健设计是在不确定性行驶工况存在的前提下，降低整车经济性能对其敏感度，即当行驶工况在一定范围内变化时，整车经济性能更稳定。文献[7-8]考虑设计变量的不确定性，采用6σ稳健设计方法对传动系参数和永磁同步电机参数进行优化设计，未考虑行驶工况对整车性能的影响；文献[9-10]考虑负载、路面的不确定性对动力系统部件参数进行优化设计，但是对行驶工况的不确定性描述存在局限性、未考虑工况对整车经济性的影响。

本文定义载荷、路面条件、道路坡度等运行条件为多因素行驶工况，提出基于多因素行驶工况的动力系统部件参数多指标稳健设计方法。构造工况仿真的响应面模型，制订试验设计方案以获得设计变量的最佳水平组合方案。

1　动力系统参数多指标稳健设计方法

1.1动力系统参数多指标稳健设计模型

电动汽车动力系统部件参数稳健设计的原理如图1所示。

图1　动力系统参数稳健设计原理

由于行驶工况的各因素具有不易或不能控制的特点，因此将其作为不可控参数，设为稳健设计模型中的噪声因子D。提取动力系统各部件的主要特征参数作为设计变量，设为控制因子X。纯电动汽车的低耗能是其主要竞争优势，然而续驶里程短和购买价格高是限制其进一步推广的关键因素。纯电动汽车的开发需在保持低耗能优势的前提下，以提高续驶里程和降低购买价格作为设计指标。因此以工况续驶里程、工况能耗和部件成本三者作为综合经济性能指标作为稳健设计模型中的输出响应F(·)。

电动汽车动力系统部件参数稳健设计的目的是在不确定性的多因素行驶工况影响下，保证动力性要求，整车的经济性能仍能达到较高水平，因此建立如下形式的多指标稳健设计数学模型：

(1)

s.t. Xl≤X≤Xu

Dl≤D≤Du

g(X)≥0

式中，X为设计变量；D为多因素行驶工况；f(·)为目标函数，包括工况能耗函数fe、工况续驶里程函数fs、部件成本函数fc；Xl、Xu分别为设计变量的下界、上界；Dl、Du分别为行驶工况各因素的下界、上界；g(X)为动力性能函数，包括最高车速、加速时间、最大爬坡度等函数。

为提高计算效率，fe、fs通过构造工况仿真的径向基函数(radialbasisfunctions，RBF)响应面模型实现计算。fc主要考虑电池和电机成本，即fc=Cbat+Cmot，其中电池成本Cbat=NbCahVbC，电机成本[11]Cmot=140Pm+2720。这里，Nb为单体电池个数，Cah为电池容量，Vb为单体电压，C为电池单价，Pm为电机峰值功率。fe、fs、fc之间的平衡通过加权系数的分配实现，设加权系数分别为w1、w2、w3，则可建立综合经济性能指标函数F(·)：

(2)

1.2动力系统参数多指标稳健设计计算流程

基于多因素行驶工况的纯电动汽车动力系统部件参数多指标稳健设计问题的基本计算流程如图2所示。

图2　动力系统参数稳健设计计算流程

计算流程具体步骤为：①建立多指标稳健设计的数学模型。②对行驶工况各因素进行分析，建立表达噪声因子不确定性的概率模型，并选取试验水平取值；通过部件分析，选取部件特征参数作为控制因子，并确定控制因子的取值范围和水平。③基于Modelica建立整车性能仿真模型，基于RBF建立工况仿真的响应面模型。④分别设计噪声因子、控制因子试验方案，基于内外表生成组合试验方案。对每个试验方案，计算综合经济性能指标函数。⑤对试验结果进行极差分析，确定各因素对综合性能指标函数的影响顺序及最佳控制因子水平组合。⑥对最佳水平组合的整车经济性和动力性进行仿真验证，判断是否满足设计要求，如果不满足则返回步骤②，调整控制因子的取值。

2　控制因子、噪声因子确定

2.1动力系统参数多指标稳健设计模型

动力系统参数稳健设计问题中的控制因子即设计变量，需要合理选取能表征电池、电机和传动系等部件的特性参数作为设计变量，还需确定每个设计变量的取值范围。

2.1.1动力电池

电池作为纯电动汽车唯一的能量源，需要满足整车的功率和能量需求，且对整车成本和重量也有较大影响。取Nb作为设计变量，Nb需满足以下要求：

(3)式中，ηb为平均放电效率；k为最大放电倍率；Dod为放电深度；ηm为电机系统效率；ηt为传动效率；m、g、f分别为整车质量、重力加速度、滚动阻力系数；Cd、A、ρ分别为空气阻力系数、迎风面积和空气密度；v、S分别为车速、续驶里程。

2.1.2驱动电机

纯电动汽车运行时，电机始终参与工作。电机功率过大将导致运行效率低且后备功率浪费；功率过小将影响整车动力性，同时电机的效率特性对整车经济性的影响较大，因此应选取能表征电机功率、效率特性的参数作为设计变量。

电机的额定工作特性须满足整车巡航行驶和最大爬坡度要求，加速要求通过过载区间满足。经式(4)、式(5)可分别获得以最高车速vmax行驶的功率P1和以一定车速vp行驶在最大爬坡度αmax上的功率P2；额定功率Pr取两者中的较大者，峰值功率Pm=λPr，即Pm是Pr的λ倍，λ为过载系数。具体算法如下：

(4)

(5)

确定了最高转速nm之后，基速nr=nm/α，α为基速比。α和λ可确定恒功率区间和过载区间。由于内置式永磁同步电机的高效率区间位于恒功率区间和过载区间的交汇区域，所以α、λ也间接反映了电机的高效率区间。因此取α和λ作为设计变量。

2.1.3传动系

电机输出轴与驱动轮之间需要安装变速传动系统，取传动比i作为设计变量。由于电机调速范围较宽，可采用一档直接驱动，i需要满足最高车速、最大爬坡度和附着力的要求：

(6)

式中，nm为电机最高转速;r为车轮半径;Fimax为αmax对应的驱动力;Tmax为电机峰值转矩;Fz为驱动轮法向反作用力;φ为附着系数。

2.2噪声因子

选取载荷、滚动阻力系数和道路坡度三个因素表征不确定性的行驶工况，定义为多因素行驶工况，作为稳健设计问题中的噪声因子。

滚动阻力系数受轮胎类型、车速、胎压、路面条件等因素影响，对于良好或一般的路面，一般取0.01～0.018和0.018～0.02。因此设置其取值区间为0.01～0.02。设载荷的取值区间为m1～ m2。采用概率方法处理不确定性的滚动阻力系数和载荷，基于正态分布N(μ,σ2)来表征。正态分布的均值μ、均方差σ分别为

μ=(xu+xl)/2

(7)

σ=(xu-xl)/6

(8)

式中，xu、xl分别为取值范围的上下界线。

为了便于试验设计，将正态分布进行离散化，依概率均匀分布原则，选择水平取值。在[xl,xu]的范围内，平均划分为N个区域，每个区域的面积相等，即随机点落入各区域的概率是一样的，因此可以选择N个区域的N+1个节点值作为水平取值。

选取基于道路坡度信息的NEDC工况[1,12]作为噪声因子之一。JTGB01-2014《公路工程技术标准》里规定了道路等级对应的设计速度、最大纵坡及最大坡长限值。根据技术标准中不同坡度下的坡长限值，在NEDC中分别设置最大坡度为3%(工况1)、4%(工况2)、5%(工况3)的坡度信息，如图3所示。

3　工况仿真的RBF响应面模型构造

电动汽车是一个包括机电液控等的多领域复杂物理系统。基于多领域统一建模语言Modelica[13]可良好地建立电动汽车整车仿真模型。在稳健设计过程中，计算耗时长，尤其是涉及到工况仿真的能耗和续驶里程计算。本文基于RBF构造fe和fs的响应面模型，以提高计算效率。

3.1基于Modelica的整车性能仿真模型

(a)工况1

(b)工况2

(c)工况3图3　基于道路坡度信息的NEDC工况

图4　纯电动汽车整车仿真模型

基于Modelica建立电动汽车前向仿真平台，如图4所示，实现整车动力性和经济性的计算。整车模型中包括参数化的电池、电机、传动系、底盘等模型，以及制动系、驾驶员、路况天气等模块。基于整车模型可分别建立加速时间、最高车速、最大爬坡度、续驶里程和工况跟随的仿真模型，实现g(·)、fs、fe的计算。

3.2工况仿真的RBF响应面模型

采用具有高精度、快速估值等特点的径向基函数进行工况仿真的响应面模型构建。径向基函数[14]的基本形式为

(9)

γ=A-1y

(10)

基于优化的拉丁超立方试验设计获得采样点，构造响应面模型的计算步骤如图5所示。

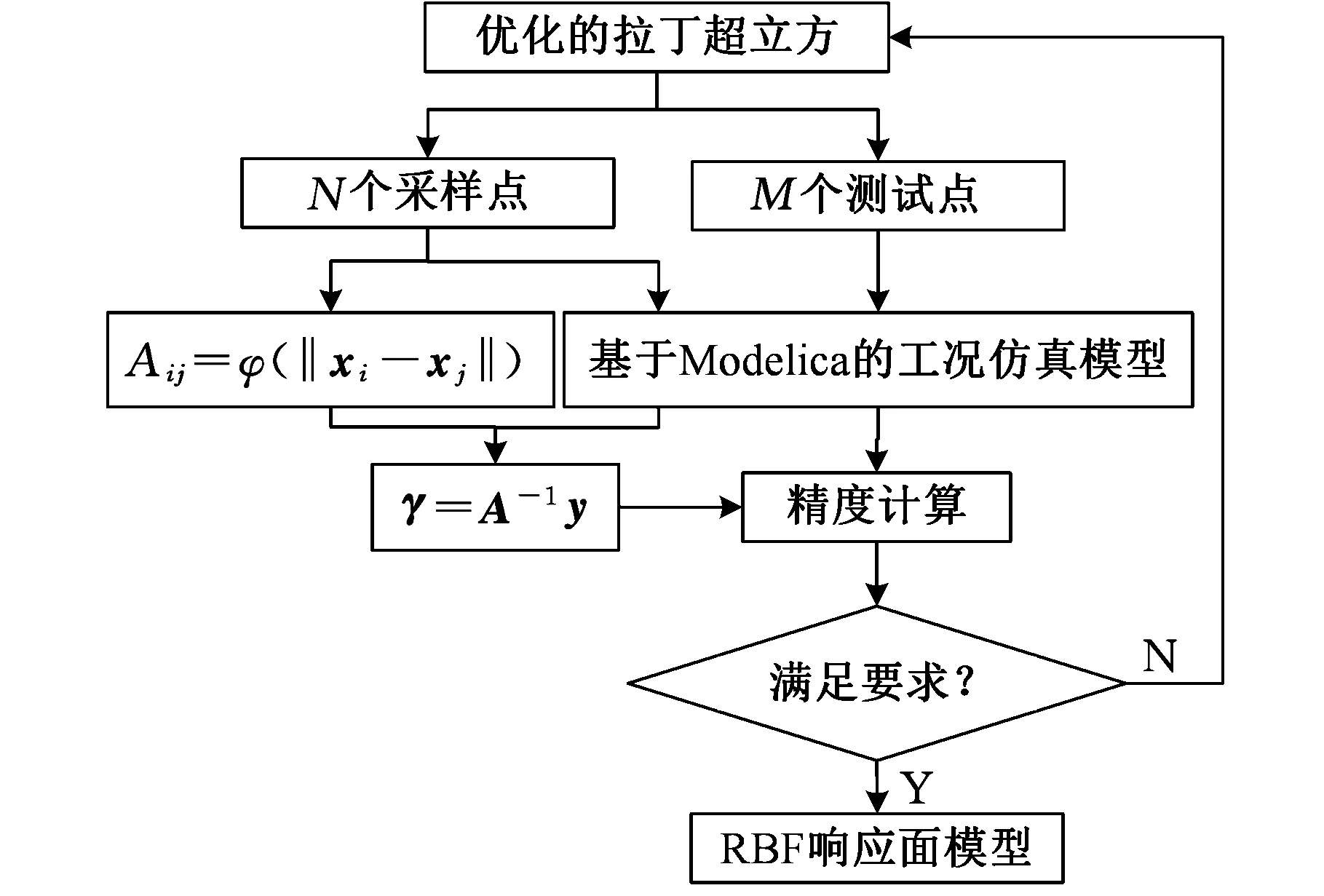
图5　工况仿真的RBF响应面模型构造流程

采用均方根误差ERMSE和R2进行精度验证[14]，其计算公式为

(11)

(12)

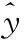
4　实例验证

以本研究中心所开发的某款纯电动公交车EVBus为研究对象，其整车基本参数及动力性设计要求如表1所示。

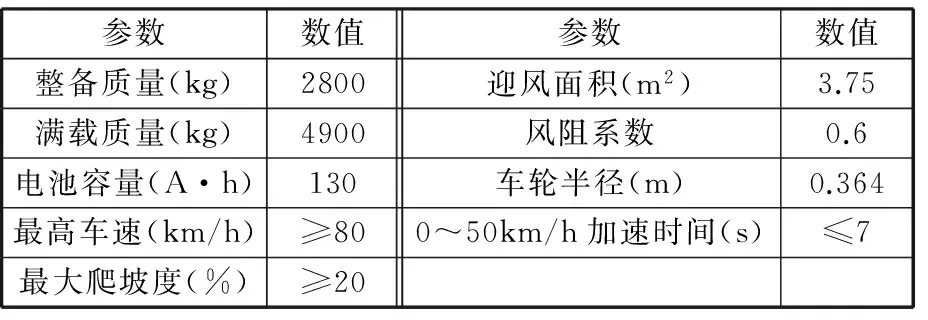
表1　EVBus基本参数和性能要求

4.1仿真模型验证与RBF响应面模型构造

在松山湖某路线行驶进行实车试验，并获得运行的速度时间图。将试验工况导入整车仿真模型进行计算，对实车试验结果与仿真计算结果进行比较分析，如图6所示。

由图6对比结果可见，仿真模型可以良好地跟随实际测试工况。由于受风力、路面条件等因素影响，试验的能耗值偏高，但偏差较小，整车仿真模型精度可靠。

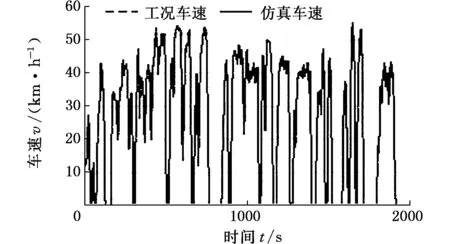
(a)车速

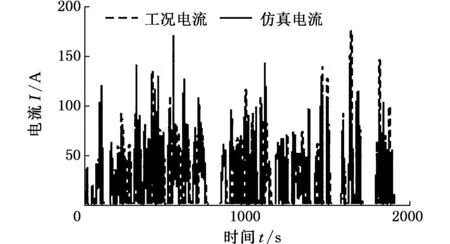
(b)电流

(c)能耗图6　实测与仿真结果对比

表2　基于RBF的响应面模型精度

4.2试验方案设计

4.2.1噪声因子试验设计

滚动阻力系数分布为f～N(0.015,0.001 672)，整车负载的取值区间为60～2100 kg，因此载荷的分布为：m～N(1080,3402)。在滚动阻力系数和载荷的取值范围内，平均划分为9个区域，获得概率均匀的10个水平值，如图7所示。基于道路坡度信息的NEDC工况有3个水平。采用全因子组合方法生成噪声因子的试验方案，共300个。

(a)滚动阻力系数

(b)载荷图 7　区间划分及水平取值

4.2.2控制因子试验设计

将整车参数代入式(3)求得Nb≥115；根据式(4)、式(5)求得Pr=50 kW；根据式(6)求得7.11≤i≤12.0。各控制因子在设计空间内分别选取4个设计水平，具体数值见表3。

表3　设计变量取值水平

采用正交试验设计生成控制因子的试验方案，根据表3中控制因子和水平的数目，选用正交表L32(44)建立试验矩阵，共32个。

4.2.3组合试验设计

基于内外试验设计表产生试验方案。将噪声因子安排在外表中，将控制因子安排在内表中，对噪声和控制因子的每次试验次序组合作为一次试验，如表4所示。

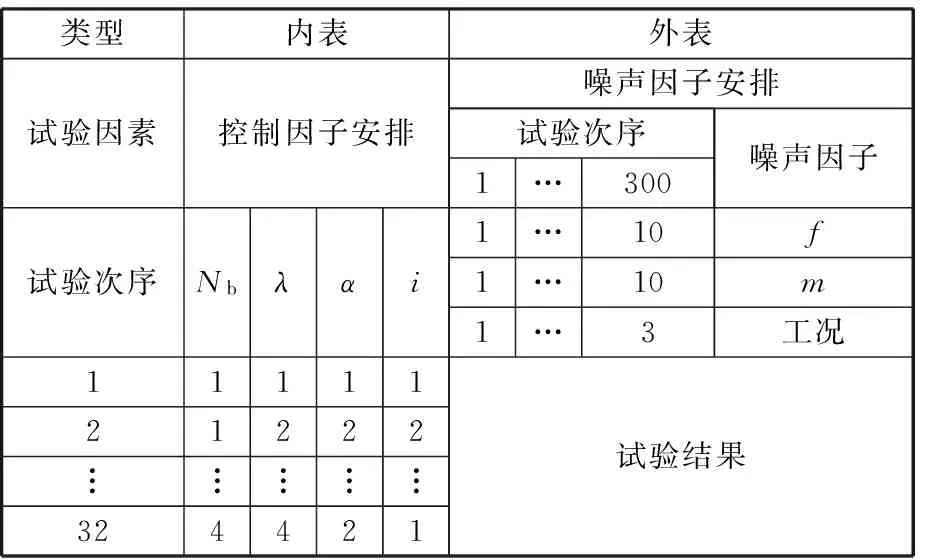
表4　组合试验设计表

4.3试验结果及分析

综合性能指标函数值的极差分析结果如表5和图8所示。表中T1～T4为各控制因子的各个水平试验结果之和；R1～R4为各控制因子的水平和的均值；R为各控制因子的极差。

表5　极差分析

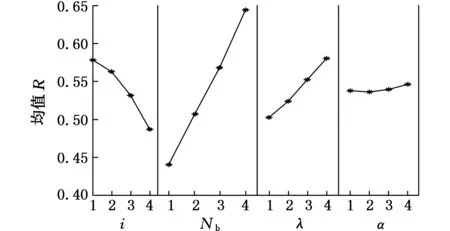
图8　极差主效应图

从表5中可以看出极差大小为：R(Nb)>R(i)>R(λ)>R(α)。图9中显示了各控制因子的水平变动时综合性能指标函数的变化情况。各控制因子对综合函数的影响程度是不同的，其中电池个数的影响最显著，其次为传动比和电机过载系数，电机基速比对综合函数的影响最小。综合性能指标函数的最佳水平组合是(Nb，i，λ，α)=(115，12.0，2.31，2.54)。

图9　综合性能指标分布对比

当式(1)中的行驶工况D为确定的，对其进行多目标优化，此时的最佳水平组合是(Nb，i，λ，α)=(122，12.0，2.31，2.54)，电机和传动比与稳健设计方案相同，电池个数有所增加。基于整车性能仿真模型对两组水平组合分别进行计算，整车性能对比如表6所示。

由表6可见，稳健设计方案的整车动力性能与多目标优化方案的基本相同，且均能满足设计要求；稳健设计方案的工况耗电量略有降低，由于电池个数减少了5.7%，续驶里程随之减少了4.8%，部件成本相对降低了5.5%。

表6　整车性能对比

应用蒙特卡罗分析分别对两组设计方案进行分析。设置随机采样次数为1000，综合函数的概率分布如图9所示。稳健设计方案的综合性能指标函数均值从0.41减小为0.35，降低了15%；方差由1.54减小为1.01，降低了34%。可见稳健设计方案不仅使得综合函数的均值降低，其离散程度也有效降低。

5　结论

本文综合考虑载荷、路面条件、道路坡度、速度等工况因素对整车经济性的影响，提出一种基于多因素行驶工况的电动汽车动力系统部件参数的多指标稳健设计方法。通过分析确定了设计变量，采用概率方法描述行驶工况的不确定性。基于RBF建立了工况仿真的响应面模型，用于分析行驶工况对经济性的影响和计算综合性能指标函数值，提高了计算效率。基于内外表设计试验方案，获得最佳水平组合。实例计算表明，通过考虑行驶工况的不确定性，稳健设计方案的综合性能指标函数的均值和方差均得到有效改善，验证了该方法的可行性。

[1]付永恒. 基于路况信息的混合动力汽车控制策略研究[D]. 北京：北京交通大学, 2011.

[2]Murgovski N, Johannesson L, Sjöberg J, et al. Component Sizing of a Plug-in Hybrid Electric Powertrain via Convex Optimization[J]. Mechatronics, 2012, 22(1): 106-120.

[3]Pourabdollah M, Murgovski N, Grauers A, et al. Optimal Sizing of a Parallel PHEV Powertrain[J]. IEEE Transactions on Vehicular Technology, 2013, 62(6): 2469-2480.

[4]赵韩，冯永恺，黄康. 纯电动汽车变速器传动比区间优化[J]. 中国机械工程, 2015,26(5): 698-703.Zhao Han, Feng Yongkai, Huang Kang.Transmission Ratio Interval Optimization for Electric Vehicle[J]. China Mechanical Engineering, 2015,26(5): 698-703.

[5]Ostadi A, Kazerani M. Optimal Sizing of the Battery Unit in a Plug-in Electric Vehicle[J]. IEEE Transactions on Vehicular Technology, 2014, 63(7): 3077-3084.

[6]Roy H K, Mcgordon A, Jennings P A. A Generalized Powertrain Design Optimization Methodology to Reduce Fuel Economy Variability in Hybrid Electric Vehicles[J]. IEEE Transactions on Vehicular Technology, 2014, 63(3): 1055-1070.

[7]陈洪燕. 基于Modelica的车辆动力性与燃油经济性6σ稳健优化设计[D]. 武汉：华中科技大学, 2009.

[8]Meng X, Wang S, Qiu J, et al. Robust Multilevel Optimization of PMSM Using Design for Six Sigma[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3248-3251.

[9]高世杰. 双响应面鲁棒设计在乘用车传动系统参数匹配中的应用[J]. 上海汽车, 2006(11): 27-30.

Gao Shijie.Application of Dual Response Surface Robust Method in Parameters Matching of Transmission System in Passenger Car [J]. Shanghai Auto, 2006(11): 27-30.

[10]王婷婷，陈潇凯，林逸. 车辆混合动力系统不确定性传播与参数优化[J]. 农业机械学报, 2013,44(8): 21-26.

Wang Tingting, Chen Xiaokai, Lin Yi.Uncertainty Propagation and Parameter Optimization of Power System in Hybrid Electric Vehicle[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013,44(8): 21-26.

[11]Wu X, Cao B, Li X, et al. Component Sizing Optimization of Plug-in Hybrid Electric Vehicles[J]. Applied Energy, 2011, 88(3): 799-804.

[12]Jeon S, Jo S, Park Y, et al. Multi-mode Driving Control of a Parallel Hybrid Electric Vehicle Using Driving Pattern Recognition[J]. Journal of Dynamic Systems, Measurement, and Control, 2002, 124(3): 143.

[13]李志华，喻军，杨红光. 偏微分方程与微分代数方程的一致求解方法[J]. 中国机械工程, 2015,26(4): 441-445.

Li Zhihua, Yu Jun, Yang Hongguang. Consistent Solving Method of PDE and DAE[J]. China Mechanical Engineering, 2015,26(4): 441-445.

[14]Regis R G. Stochastic Radial Basis Function Algorithms for Large-scale Optimization Involving Expensive Black-box Objective and Constraint Functions[J]. Computers & Operations Research, 2011, 38(5): 837-853.

(编辑王旻玥)

Multi-objective Robust Design of Electric Vehicle Powertrain Parameters

Yu Limin1Xiong Huiyuan1,2Zong Zhijian1,2Wu Yizhong3

1.Sun Yat-Sen University,Guangzhou,510006 2.Institute of Dongguan-Sun Yat-Sen University,Dongguan,Guangdong,523808 3.Huazhong University of Science and Technology,Wuhan, 430074

In order to reduce the influences of dynamic driving cycle on economy performance, a multi-objective robust design method for electric vehicle powertrain parameters was presented based on multi-factor driving cycle. With cycle energy consumption, cycle driving range and component cost as comprehensive economy function objectives, battery, motor and transmission parameters as design factors, driving cycle as noise factors, a robust design model for powertrain parameters was proposed, and vehicle performance simulation model was built based on Modelica. A response surface model of cycle simulation was built based on radial basis functions. The uncertainty description of driving cycle was based on probability theory, the design of experiments was carried out to solve the problem. Taking EVBus for example, simulation results show that the means and variances of the comprehensive economy function objectives are improved effectively based on Monte Carlo analysis, which proves the effectiveness of the method.

electric vehicle; robust design; driving cycle; radial basis function(RBF)

2015-11-30

国家自然科学基金资助项目(51575205)；广东省重大科技专项(2016B010118001)；东莞市重大科技项目(201521511902)

U462.1

10.3969/j.issn.1004-132X.2016.20.023

于丽敏，女，1987年生。中山大学工学院博士研究生。主要研究方向为电动汽车动力系统参数优化设计。熊会元(通信作者)，男，1973年生。中山大学工学院副教授，东莞中山大学研究院电动汽车中心主任助理。宗志坚，男，1963年生。中山大学工学院教授,东莞中山大学研究院院长。吴义忠，男，1970年生。华中科技大学机械科学与工程学院教授。