面向多因素多目标的模具光整加工工艺
2016-11-02计时鸣金明生黄希欢
计时鸣 韦 伟 金明生 张 利 黄希欢 潘 烨
浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点试验室,杭州,310032
面向多因素多目标的模具光整加工工艺
计时鸣韦伟金明生张利黄希欢潘烨
浙江工业大学特种装备制造与先进加工技术教育部/浙江省重点试验室,杭州,310032
基于灰度关联分析法、TOPSIS分析法及层次分析法,提出一种针对模具光整加工工艺研究的多因素多目标分析方法。该方法采用灰度关联法来分析多加工参数之间的关联度,利用TOPSIS分析多加工质量评价标准间的关联度,通过层次法获得合理的主客观结合的权重矩阵,并可通过方差分析(ANOVA)获得各加工参数对每个标准的影响程度及相关预测模型。将该方法应用于激光强化模具表面光整加工的工艺研究中,研究结果验证了该方法的实用性和有效性。
加工参数;加工质量;光整加工;加工工艺
0 引言
模具广泛应用于电子、仪器、电器和通信等产品生产制造中。模具加工水平已成为衡量一个国家产品制造水平的重要标志,决定着产品质量、生产效益。模具激光表面强化处理技术作为现代制造业中最具代表性的高效和绿色的表面处理技术,能使模具表面的硬度和耐磨性大幅度提高,光整加工作为模具加工过程中最后一道工序,决定着模具的质量以及使用寿命[1-2]。
激光强化模具的表面光整加工中,加工表面的材料去除量及表面粗糙度作为主要评价加工质量标准,相互影响,相互制约。材料去除量的增大过程中,粗糙度相应先减小后增大,同时光整工具的下压量、磨粒粒度、加工转速、充气压力等[3-7]加工参数不仅相互响应,并且直接影响加工质量和效率。因此,合理地选择加工参数对确保模具质量、提高生产率、降低生产成本起着重要作用。
面向加工质量的模具光整工艺研究是对多质量评价标准关联多因素加工参数的研究。模具光整工艺中的各因素间的关联性可通过灰色关联分析方法计算灰色关联度来表征[8-10],但灰色关联分析方法不能描述多评价标准间的关联度。层次分析法能够对决策过程进行层次化,使用定性和定量有机结合计算权重,实现定量化决策,但其分析目标只考虑单一评价。TOPSIS法适用于多评价标准的权衡决策,是对多个方案进行比较选择的分析方法[11-12]。
目前,无论是田口试验设计,还是正交试验设计,虽然都能为工艺研究提供试验方案,但尚未有一种公认的、体系性的方法可用于工艺研究。为合理确定模具光整加工参数,迎合各种加工需求,设计一种模具光整加工工艺研究方法对今后的光整加工工艺研究有积极的指导意义。本文通过设计光整加工方案,首先确定主要加工参数,利用灰度关联法计算各参数间的关联度;其次运用TOPSIS法对多评价标准进行关联;然后引入层次分析法对关联度中的权值进行计算;最后,通过实际工业加工案例验证该方法的有效性和可行性。
1 多因素多目标分析方法
1.1光整加工方案设计
正交试验是寻求最优参数组合、分析各影响因素和影响水平的一种有效试验方式,其特点是以较少试验次数、较短试验时间和相对较低的试验费用来获得试验结果。设n个光整加工参数的集合P = {p1,p2,…,pn},相应参数的m个水平集合L={l1,l2,…,lm},则正交试验设计的加工方案总数g = nm;设t个评价标准为集合C = {c1,c2,…, ct}。
1.2多加工参数关联度分析
灰度关联分析的目的是通过单一加工评价标准的试验值计算多加工参数间的关联度,并将试验值归一化,生成相应的灰度关联因子(GRC)来关联期望值与实际值。对各反馈的GRC进行均值化以求得各试验方案的等级排序,从而获得多参数混合的试验方法。主要通过以下5个步骤对多加工参数进行关联度分析。
(1)在分析参数关联度时,由于各参数关联度相近或参数选取较多,需对参数进行优化处理,计算各目标的试验数据的信噪比y(k)S/N:
(1)
式中,k表示第k个评价标准;r为某组试验方案的重复试验次数;yi为第i次试验值。
通过信噪比的计算来放大目标数据,其值越大则该方案的评价结果越好。
(2)进行标准化处理,即基于信噪比放大后的数据计算第k个标准第j组试验的标准化值xj(k):
(2)
k=1,2,…,tj=1,2,…,g
该式主要是将试验数据进行归一化处理,所有数据归到同一段合理的区间内。
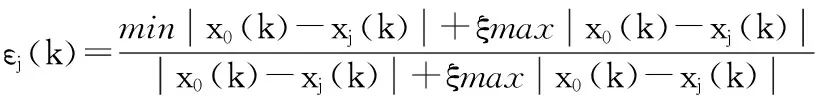
(3)
式中,εj(k)为第k个标准的第j组方案试验数据的GRC;x0(k)为参照数(取最优组);xj(k)为对比组;ξ为判断因子,定义0≤ξ≤1,一般取0.5。
(4)对每组试验方案中g个标准的GRC进行均化,通过下式计算得到灰度关联级(GRG):
(4)
式中,γj为GRG代表面向n个试验目标的第j组试验方案在g组试验方案中的排序。
(5)基于上述排序,对每个光整加工参数,对应其不同水平,计算GRG的平均值,最后得到各参数对评价标准的响应度。
1.3多加工评价标准关联度分析
TOPSIS法通过检测评价对象与最优解、最劣解的距离来进行排序,若评价对象最靠近最优解同时又最远离最劣解,则为最好;否则为最差。
(1)生成g×t维决策矩阵D,通过下式进行标准化:
(5)

(2)计算每个标准在所有标准中所占的权重,即衡量标准的重要性,生成对应决策矩阵的权重矩阵W。
(3)对决策矩阵进行加权处理,得到加权决策矩阵V=[vik]:
(6)
(4)通过下式确定最优和最劣加工方案:
(7)

(5)通过下式分别计算各标准与最优及最劣方案的偏差:
(8)

(6)基于最优及最劣方案的偏差,通过下式综合计算各方案的贴近度CCi:
(9)
(7)根据贴近度CCi从大到小对各方案进行排序[13],贴近度CCi值越大,该方案越优,CCi值最大为最优方案。
1.4权值计算
在建立评价体系时,各标准对决策的重要性各不相同,通常用权重值来描述各标准的重要性,权重值越高,标准的重要性越大。权重的设定通常分为主观设定和客观设定,主要表达决策人对每个标准的重视程度、各标准的差异程度及各标准的可靠程度。采用层次分析法将定性定量因素、主客观判断方法有机地结合起来,科学地定义权重。
(1)建立层次结构,如图1所示。

图1 加工方案层次分析图
(2)根据评价标准,构造t×t的比较矩阵J,J中的元素jpq表示相对权重值:
cp:cq⟹jpq
(10)
其中,cp为标准p的权重值,cq为标准q的权重,cp+cq=1,0≤cp≤1且0≤cq≤1。jpq意义如表1所示,jpq> 0且jpq=(jpq)-1。

表1 权重值意义表
(3)对J进行一致性检验,定义一致性指标CI:
(11)其中,λ为J的特征值。若CI=0,有完全的一致性;若CI接近于0,有满意的一致性;若CI越大,不一致越严重。考虑当CI>1时,对J作出修改。
2 实例分析与讨论
2.1工业应用实例
软固结磨粒气压砂轮的光整加工工艺研究中,在忽略其他加工环境因素的条件下,基于Preston理论中加工参数对材料去除的描述,本文采用气压砂轮的充气压力、转速及下压量3个主要加工参数以及3个不同水平取值设计光整加工试验,如表2所示,故共有27组试验方案。加工质量评价标准为材料除去量Mr和表面粗糙度Ra。

表2 光整加工因素和水平分布表
根据1.2节的灰度关联分析及27组试验,对加工的单评价标准对应的加工参数进行分析,得到表3所示各参数间的关联值,并且对所有方案进行了排序。为得到各参数具体对应的水平值之间的关联度,通过这种关联度来表示该参数的影响程度,基于表3分析得到表4。表4不仅描述各参数间的关联度,也描述参数水平对加工的影响度。通过表3和表4,优选第1为第14组试验方案,即为最优加工参数组合,p=0.05 MPa,n=1250 r/min,d=2 mm。关于加工参数的灰度关联值对试验方案的排序:14,10,13,15,12,16,11,7,1,3,2,4,8,19,6,17,22,18,9,5,25,23,20,24,21,26,27。

表3 正交试验下加工参数关联度分析表

表4 加工参数灰度关联排序表
基于1.4节所述,对加工的评价标准进行权重定义,加工粗糙度略重要于材料去除质量,计算重矩阵过程如下:

根据1.3节中的TOPSIS分析法,结合权重矩阵,对评价标准间的关联度进行描述,分析得到表5,其所述数据是对加工评价标准的数据值进行标准化、权重标准化,以及标准化间贴近度的计算。基于对各参数的灰度关联值,考虑加工质量评价标准,方案排序变为:21,26,27,23,5,20,4,2,1,24,7,8,6,3,9,25,19,22,17,10,18,13,11,16,12,14,15。
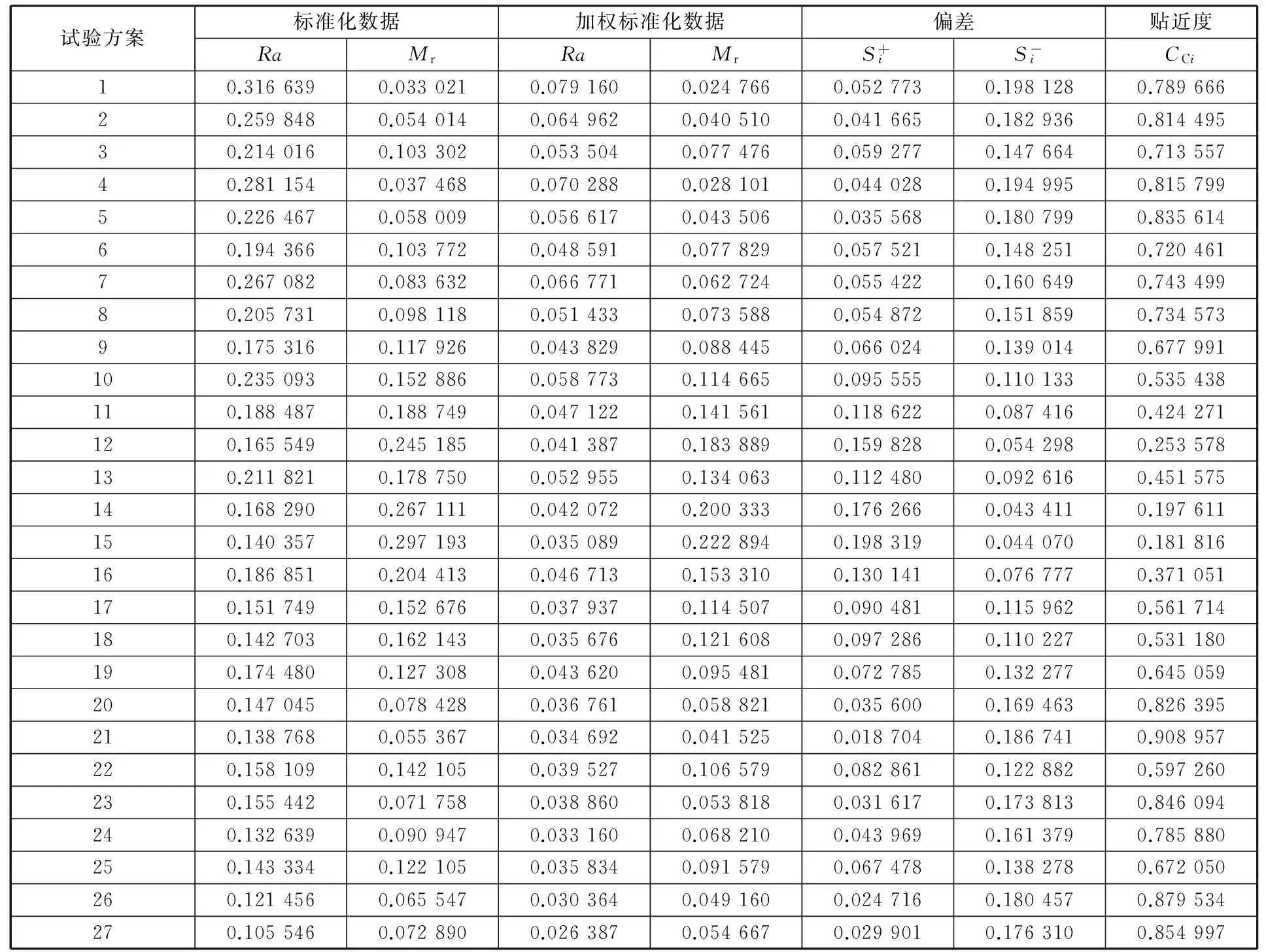
表5 标准化、权重标准化及贴近度数据表
2.2讨论分析
响应面分析法[14]是一种广泛应用于产品工艺参数设计及工艺过程优化的统计方法,主要用于研究输入参数对输出响应的影响,可表示为
(12)
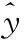
利用Minitab软件对加工评价标准Mr和Ra进行回归分析,得到关于Mr和Ra的拟合方程分别为
Mr=0.903+2.72p-0.00126n+0.148d-
4.8p2+0.000001n2-0.016d2+
0.00396pn+0.053pd+0.000114nd
(13)
Ra=1.127-12.89p-0.000655n-0.1145d+
63.41p2+0.0000001n2-0.0189d2+
0.00242pn+1.503pd+0.000078nd
(14)
通过方差分析(ANOVA),对Mr和Ra的响应曲面进行验证,结果如表6和表7所示。对于Mr,其R2为97.12%,调整R2为95.60%,预测R2为93.36%。对于Ra,其R2为88.40%,调整R2为82.26%,预测R2为85.50%。由于式(13)的R2接近100%,则Mr接近理想;由于式(14)的R2接近90%,则Ra的拟合方程具有一定的参考价值。
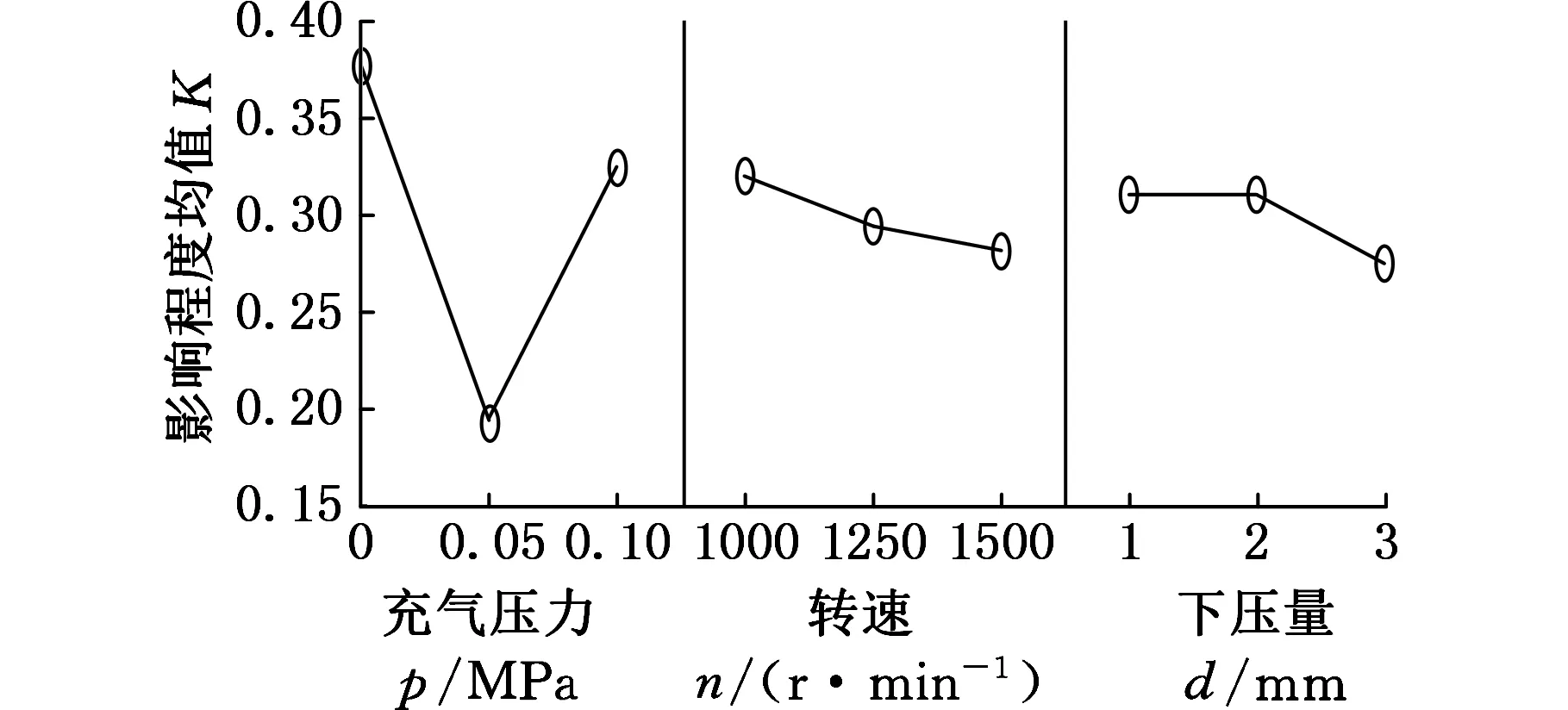
图3 粗糙度Ra主效应图
首先,通过Mr响应曲面的ANOVA,得到图2关于Mr的主效应图。由图3可知,充气压力p是主要影响因素,其次是下压量d,最后是转速n。这主要是由于增大的充气压力直接影响到材料的切削力,下压量的增大直接导致接触面积增大,而转速可能水平区间过窄,减小了转速的影响。然后,通过Ra响应曲面的ANOVA,得到图3关于Ra的主效应图,充气压力p是主要影响因素,其次是转速n,然后是下压量d。
3 结论
(1)通过对模具光整加工工艺的正交试验方案的分析,提出一种基于灰度关联法、TOPSIS分析及层次分析法的分阶段多分析法,可用于研究多因素多目标模具光整加工工艺。该方法同时考虑加工参数及加工质量对方案优选的影响,对加工工艺的研究具有普适性和系统性,可广泛用于各种加工工艺的研究,从而控制实际生产品质。
(2)该方法采用灰度关联法分析了多加工参数之间的关联度,并通过灰度值优选出关于多因素的最优加工参数组合;利用TOPSIS分析了多加工质量评价标准间的关联度,通过层次法获得合理的主客观结合的权重矩阵,科学地优选出多目标加工方案;通过ANOVA获得各加工参数对每个标准的影响程度及相关预测模型。
(3)将该方法应用于软固结磨粒气压砂轮的光整加工工艺研究,采用气压砂轮的充气压力、转速和下压量进行了试验设计,以表面粗糙度和材料去除率为评价标准进行了分析,得到加工工艺方案的排序及最优方案。该方法具有一定的可行性和科学性,有利于指导其他加工工艺研究。
[1]周圣丰,戴晓琴,郑海忠.激光熔覆与激光感应复合溶覆WC-Ni60A涂层的结构与性能特征[J].机械工程学报,2012,48(7): 113-118.
ZhouShengfeng,DaiXiaoqin,ZhengHaizhong.CharacteristicsonStructureandPropertiesofWC-Ni60ACoatingsbyLaserCladdingandLaser-inductionHybridCladding[J].JournalofMechanicalEngineering, 2012, 48(7):113-118.
[2]KwokCT,LeongKI,ChengFT,etal.MicrostructuralandCorrosionCharacteristicsofLaserSurface-meltedPlasticsMoldSteels[J].MaterialsScience&EngineeringA, 2003, 357(1/2):94-103.[3]高波.气囊抛光试验样机研制及其关键技术研究[D].哈尔滨:哈尔滨工业大学,2005.
[4]金明生.模具自由曲面气囊抛光机理及工艺研究[D].杭州:浙江工业大学,2010.
[5]曾晰.软固结磨粒气压砂轮设计方法及材料去除特性研究[D].杭州:浙江工业大学,2013.
[6]吕哲. 超声振动辅助磨料水射流抛光冲蚀机理和工艺技术研究[D]. 济南:山东大学, 2015.
[7]Puertas I, Luis C J. A Study of Optimization of Machining Parameters for Electrical Discharge Machining of Boron Carbide[J]. Materials & Manufacturing Processes, 2004, 19(6):1041-1070.
[8]Saikumar S, Shunmugam M S. Parameter Selection based on Surface Finish in High-speed End-milling Using Differential Evolution[J]. Mater.Manuf. Processes, 2006,21 (4): 341-347.
[9]Deng J. Introduction to Grey Systems Theory[J]. J. Grey Syst. 1989,1 (1): 1-24.
[10]Pan L K, Wang C C, Wei S L, et al. Optimizing Multiple Quality Characteristics via Taguchi Method-based Grey Analysis[J]. Journal of Materials Processing Technology, 2007, 182(1/3):107-116.
[11]Dewangan S, Gangopadhyay S, Biswas C K. Study of Surface Integrity and Dimensional Accuracy in EDM Using Fuzzy TOPSIS and Sensitivity Analysis[J]. Measurement, 2014, 63(3):364-376.
[12]Parr W C. Introduction to Quality Engineering: Designing Quality into Products and Processes[J]. Technometrics, 1989, 31(2):255-256.
[13]Yayla A Y, Yildiz A, Özbek A. Fuzzy TOPSIS Method in Supplier Selection and Application in the Garment Industry[J]. Fibres & Textiles in Eastern Europe, 2012, 20(4):20-23.
[14]Richard F G. Response Surface Methodology, Process and Product Optimization Using Design Experiment[J]. Technometrics,1996, 38(3):284-286.
(编辑王旻玥)
Mold Finishing for Multi-factor and Multi-objective
Ji ShimingWei WeiJin MingshengZhang LiHuang XihuanPan Ye
Key Laboratory of Special Purpose Equipment and Advanced Processing Technology,Ministry of Education & Zhejiang Province,Zhejiang University of Technology,Hangzhou,310032
Based on gray correlation analysis, technique for order preference by similarity to ideal solution(TOPSIS) analysis and analytic hierarchy process, a multiple objectives and multiple contributing factors analysis method was put forward, which was proposed for the whole processes of the mold finishing. Gray correlation method was used to analyze the correlation degrees among multiple parameters, and TOPSIS was used to analyze the correlations among the multi-processing quality evaluation standards. Through the hierarchical method, a reasonable weight matrix was obtained, which combined the objectivity and subjectivity. The influence degree of each processing parameter on each standard and the correlation forecast model might be obtained via ANOVA analysis. Besides, this method was applied to the surface finishing of laser hardened mold, and the results manifests the method is practical and effective.
machining parameter; machining quality; finishing; processing technology
2015-12-24
国家自然科学基金资助项目(51175471,51205358,51575493)
TH162
10.3969/j.issn.1004-132X.2016.20.019
计时鸣,男,1957年生。浙江工业大学机械工程学院教授。主要研究方向为机器人技术及其在机械加工领域的应用、精密与超精密加工技术。发表论文130余篇。韦伟,女,1985年生。浙江工业大学机械工程学院博士研究生。金明生,男,1983年生。浙江工业大学机械工程学院副教授。张利,女,1971生。浙江工业大学机械工程学院副教授。黄希欢,男,1990年生。浙江工业大学机械工程学院硕士研究生。潘烨,男,1990年生。浙江工业大学机械工程学院博士研究生。
