面向转子故障特征提取的多尺度拉普拉斯特征映射方法
2016-11-02王广斌杜晓阳
王广斌 杜晓阳 罗 军,2
1.湖南科技大学机械设备健康维护湖南省重点实验室, 湘潭,4112012.中交第二航务工程局有限公司深圳分公司,深圳,518067
面向转子故障特征提取的多尺度拉普拉斯特征映射方法
王广斌1杜晓阳1罗军1,2
1.湖南科技大学机械设备健康维护湖南省重点实验室, 湘潭,4112012.中交第二航务工程局有限公司深圳分公司,深圳,518067
融合多尺度分解理论和流形学习思想,提出了一种面向转子故障特征提取的多尺度拉普拉斯特征映射算法。首先对转子故障振动信号进行多尺度小波包分解,提取各独立频带信号的最优尺度小波熵,构建特征参量矩阵并估计其固有维数,然后通过拉普拉斯特征映射将特征参量数据嵌入到低维本征空间,得到故障的最敏感特征,最后融合决策实现故障的准确识别。实验表明,相对于主成分分析算法、局部线性嵌入算法和拉普拉斯特征映射算法,多尺度拉普拉斯特征映射方法提取的转子故障信号特征更容易识别。
转子系统;拉普拉斯特征映射;多尺度;特征提取
0 引言
现代旋转机械中转子系统易于发生的故障有:转子不对中、不平衡,转子裂纹,基座松动和碰摩等。上述这些故障很多都是非线性、非平稳信号,提取这类故障信号的敏感特征一直都是研究的热点和难点。传统分析方法(如频域分析、时域分析、包络分析、倒频谱分析、时间序列分析等[1-3])对非线性和非平稳故障信号潜在信息的挖掘和敏感特征的提取表现乏力。
以2000年在《Science》杂志上发表的两篇论文[4-5]为起点兴起的流形学习算法研究,使得机器学习、数据挖掘技术获得了新的动力。经典流形学习算法有等距特征映射(isometric feature mapping, ISOMAP)[4]、局部线性嵌入(locally linear embedding, LLE)[5]、拉普拉斯特征映射(Laplacian eigenmaps, LE)[6-7]、局部切空间排列(local tangent space alignment, LTSA)[8]等。近年来,对信号的多尺度分析和信号特征挖掘的思想在现代旋转机械故障诊断中凸显出了巨大优势,尤其针对微弱非平稳、非线性故障信号特征的提取优势明显。刘继伟[9]提出大数据的多尺度状态监测方法,利用尺度熵和尺度反映多尺度特性的变化,探索不同尺度的分布和对时间的变化规律。李鹏[10]采用多尺度分析方法提出一种基于小波熵的机械状态监测方法,通过调节特征频率,利用小波熵对系统参数的突变敏感性,最终实现机械和设备的监测。张龙等[11]基于轴承故障振动信号具有跨尺度复杂性的特性,提出一种新的基于多尺度熵和神经网络的滚动轴承诊断方法,将多尺度分析方法对不同的轴承故障信号进行特征提取,利用神经网络分类,最终实现轴承故障类型与故障程度的诊断。
本文融合多尺度分解理论和流形学习思想,提出一种面向转子故障特征提取的多尺度拉普拉斯特征映射算法。以转子系统为研究对象:对转子系统正常、不对中、不平衡、基座松动[12-13]四种状态,在10 Hz、20 Hz、30 Hz、40 Hz、50 Hz五种转频下依次采集并进行预处理和数据分析处理。通过比较经典的主成分分析(principal component analysis, PCA)算法、LLE算法和LE算法,证明了本文所提的多尺度拉普拉斯特征映射(multiscale-LE,MS-LE)方法提取的转子故障信号特征更容易识别。
1 多尺度分解方法
小波包分析作为多尺度分析方法里面的一种,是在多分辨分析基础上构成的一种更精细的正交分解方法,能够为信号提供一种更加精细的分析与重构方法。它将频带进行多层次划分,不仅对低频部分进行分解,而且对高频部分也进行分解,并根据被分析信号的特征,自适应地选择频带,从而提高了时频分辨率,非常适合处理非线性和非平稳信号。小波包变换选定某种小波函数后,设其滤波系数为h={hn},令gn=(-1)nh1-n,n∈Z。定义一列递归函数Wn(t),则有
(1)
(2)
k∈Z
由式(1)、式(2)所确定的{Wn(t)}即为小波包,W1(t)就是对应的小波函数。小波包对信号的分解用树型结构表示。图1是以三层小波包分解为例说明小波包分解过程示意图。

图1 小波包分解示意图
图1中,节点(i,j)表示第i层第j个节点(i=0,1,2,3;j=0,1,…,7),每个节点代表一定的信号特征。其中节点(0,0)代表原始信号S,节点(1,0)代表小波包分解的第1层低频系数x10,节点(1,1)代表小波包分解的第1层高频系数x11,其他依此类推。
2 多尺度拉普拉斯特征映射方法
首先将同种故障的数据源进行多尺度小波包分解,提取各独立频带信号的最优尺度小波熵,然后用小波熵构建特征参量矩阵并对其进行固有维数估计,以固有维数值为依据通过拉普拉斯特征映射将特征参量数据嵌入到低维本征空间,得到故障的最敏感特征,最后融合决策实现故障的准确识别。多尺度拉普拉斯特征映射方法模型如图2所示。
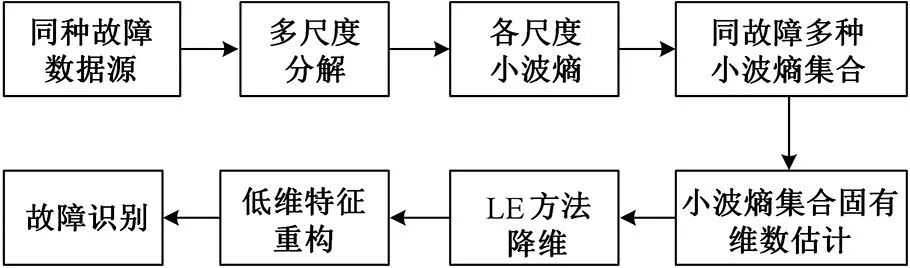
图2 多尺度拉普拉斯特征映射方法故障诊断模型
多尺度拉普拉斯特征映射方法步骤如下:
(1) 转子实验轴两端分别在横向、纵向和径向布置6(2×3=6)个加速度传感器,每种转速下每种转子状态采集1组,共4种状态和5种转速120(5×4×6=120)组。
(2)同一故障数据集X={1,2,…,N},同一种故障每一列不同状态的矩阵如下:
A=[a1a2…an]T
(3)对A=[a1a2…an]T进行小波包分解,即:小波包分解选定小波函数之后,设定其滤波系数是τ={τn},令gk=(-1)kτ1-k。可以定义递归函数:
(3)
(4)
可知{Yn(t)|n∈N}即是正交小波包,Y1(t)是对应的小波函数,且有

(5)
式中,⊕为异或逻辑运算符号。

(6)

(7)
(8)
(4)对同一故障的所有状态进行小波包分解得到M个独立频带,对频带进行小波熵Sk特征提取,即假定第j层的高频带系数是dj(k),采样点数是N,把采样点的小波系数分成n份,可以知道第k个子区间的小波系数的能量是
(9)
同时,第j层的高频带小波系数的全部能量是
(10)
可以设定第k个子区间所含有的能量在该尺度上总能量存在的概率
(11)
则第k个子区间所对应的信息小波熵
(12)
(5)N组信号的M个频带小波熵Sk构成一个M×N的小波熵高维数据矩阵PN。
(6)对M×N的高维数据矩阵PN采用极大似然估计方法得到矩阵DN的本征维数是m。
(7)以矩阵DN选取邻域点个数,构造邻域图G。假设样本点xi与样本点xj之间的欧氏距离dij小于某一个既定的阀值ε,由此可以定义样本点xi是样本点xj的近邻点。
(8)若xi和xj相邻,设定wij=e-‖xi-xj‖2/t2;反之定义wij=0。
(9)以m为依据,求低维嵌入矩阵Y,有
(13)
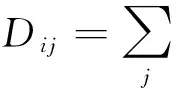
arg min tr(YLYT)
低维嵌入矩阵Y取的是拉普拉斯矩阵L里面最小的d+1个特征值所对应的特征向量(v1,v2,…,vd+1),即
Y=[v1v2…vd+1]T
(14)
(10)通过本质特征映射得到低维特征向量,提取故障特征,采用决策融合方法最终实现故障诊断。
3 转子故障诊断实验
3.1转子故障诊断实验系统
为验证多尺度拉普拉斯特征映射算法的故障诊断效果,实验采用美国Spectra Quest公司的机械故障综合实验台、美国PCB608A11振动加速度传感器和丹麦B&K公司的PULSE数据采集系统,如图3所示。在实验台两侧布置振动信号传感器,横向、径向和纵向3个方向共6个,以转子系统的正常状态、不平衡故障、不对中故障、基座松动故障为研究对象,数据采集情况如下:每一种故障在每一种转速(10 Hz、20 Hz、30 Hz、40 Hz、50 Hz)下采集1组信号,采样频率是8192 Hz,采集时间为10 s,一共120(5×4×6=120)组信号。

图3 转子故障模拟实验及数据采集
以一种故障状态为例,提出初步的解决方案:首先,分别对多个传感器数据进行多尺度小波包分解,对细节部分信号进行分解,且获取各个尺度上的最优尺度小波熵,实现潜在特征的初步挖掘。然后,以最优尺度小波熵构建特征参量矩阵并对其进行固有维数估计。最后,利用拉普拉斯特征映射方法以固有维数值为依据将高维数据的本质特征映射到低维空间中,获取故障低维特征映射向量,实现故障识别。数据的处理流程如图4所示。

图4 数据处理流程图
3.2时域和频域特性分析
对转子系统模拟实验采集的振动加速度信号进行消噪、滤波等前期处理。转子系统在某一个特定方向信号的振动特性不能完整地表达出系统整体状态,尤其不同故障之间时域分析的幅值表现各异。转频相对小的故障信号振动不够强烈,转频太大故障信号又容易受到噪声等因素的影响,这给故障诊断带来了巨大的困难。为了更好地实现故障识别,对四种状态在转频为30 Hz的情况下,对X、Y、Z(即横、纵、径向)三个方向分别进行时域和频域分析,结果如图5~图8所示。

(a)时域图 (b)频域图图5 转子正常状态信号时频图
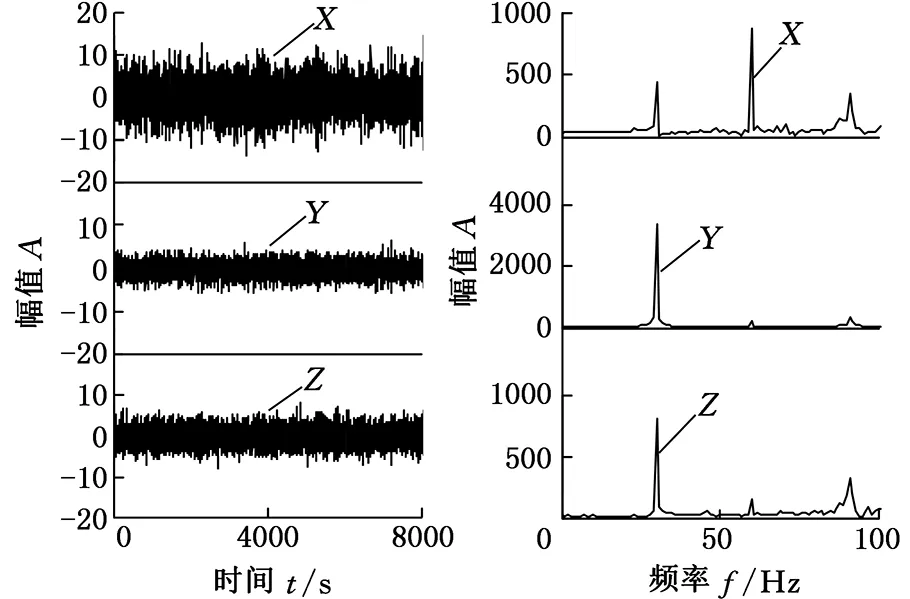
(a)时域图 (b)频域图图6 转子不平衡故障信号时频图

(a)时域图 (b)频域图图7 转子不对中故障信号时频图
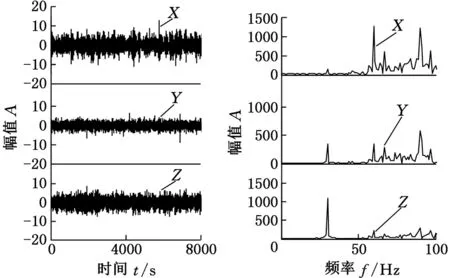
(a)时域图 (b)频域图图8 转子松动状态故障信号时频图
图5和图6分别是转子正常状态时频图和转子不平衡故障信号时频图。从图5、图6可以得出:①两种状态在X方向的幅值都比其他两个方向的大;②在X方向,2倍频处两种状态的频谱能量都很集中,不平衡故障在1倍频和3倍频处也有较低振动体现,能量相对较弱;③Y和Z方向,正常状态则在3倍频处频域幅值很大,不平衡故障主要在1倍频处频域幅值较大。
图7和图8分别是转子不对中、转子松动故障信号时频图。从图7和图8可以得出:①转子不对中、转子松动故障与转子正常、不平衡故障在时域图上的表现是完全一致的,X方向的振动幅度是最大的;②对于不对中故障,在X方向以2倍频和3倍频处的频域幅值较大,主要以3倍频为主;在Y方向1倍频处也有振动出现。对于松动故障,X方向上,在2倍频以后表现出多倍频的振动特性,由此可知松动这一非线性故障呈现出不确定性和成分丰富的特性。
综上所述发现:①在时域分析中,四种状态的X方向振动最为强烈,Y方向最弱。对其他四种转频作相同分析,也难以从X方向提取出时频特征参量作为故障特征。②在频域分析中,四种状态的X方向振动特性强弱不一,毫无规律可循。Y方向和Z方向,正常状态和不对中故障在3倍频处频域幅值很大,不平衡和松动故障频域幅值大的表现以1倍频为主,同样不利于决策分析。这四种状态在时频特性分析上极其相近,且毫无规律。倘若以时频特性参量为故障特征,无疑会给机器分类学习准确科学决策带来巨大的困难。
3.3故障诊断分析
以MS-LE的故障诊断步骤对数据进行处理,选取在转频为10 Hz、20 Hz、30 Hz、40 Hz、50 Hz工作状态下采集的120组数据来研究(4种状态,共5×4×6=120),结合经典的PCA算法、LLE算法、LE算法进行分析对比。
图9和图10分别是基于PCA故障识别图和基于LLE故障识别图。由图9、图10可知:PCA算法分析四种状态时特征向量集中在一点,无法识别故障;经典LLE算法分析四种状态时,特征向量彼此交集在一起,混乱不堪,故障类内的聚集性不好,故障类之间的分离效果欠佳。
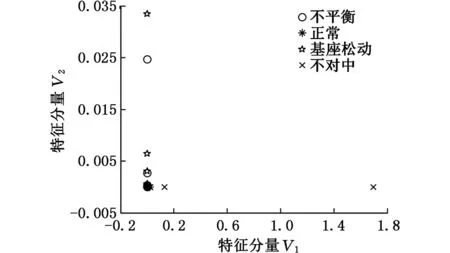
图9 基于PCA算法四种故障识别结果

图10 基于LLE算法四种故障识别结果

图11 基于LE算法四种故障识别结果

图12 MS-LE方法故障识别图
图11和图12分别是基于LE算法故障识别图和基于MS-LE方法故障识别图。LE算法对转子正常、不平衡和不对中故障有一定的识别能力,在故障类内存在一定的聚集能力,呈现出弯曲线形状,尤其是不对中故障能完全识别。不平衡故障和正常状态存在少量的交集部分。而对于松动故障的识别呈离散点分布,这一点与松动故障的非线性相契合。总的来说,LE方法对转子单故障的识别能力较好,但类内的聚集效果不理想,状态之间存在少量的交集,对于松动故障,识别能力较差。这没能达到故障识别的要求,所以不能识别故障。
图12中三个方向分别表示三个主特征分量,以此构成一个三维空间。由转子系统实验可知:①MS-LE方法不仅能识别单一故障还能区别各个故障与正常状态;②三维图下四种状态都有很好的类内聚集效果;③三维图下尽管基座松动和不平衡故障有一点接触,总的来说识别效果良好。
为了更直观地证实本文MS-LE方法的有效性,将四种故障的三维图分别映射到XY平面、XZ平面和YZ平面,与上文三种经典流形学习方法分析对比,如图13所示。
图13中的三幅图分别是图12在XY、XZ、YZ三个平面的投影。从图13可以看出:①四种故障完全能够彼此分离开来,能够达到识别目的;②松动故障的类内聚集效果不是很好,存在一定的分散情况;③正常状态在YZ平面也有分散现象出现,转子不对中故障的识别聚集效果好。
进一步将MS-LE方法应用到某特种车辆变速箱滚子轴承故障特征提取中,以验证多尺度拉普拉斯特征映射方法的有效性。以某特种车辆变速箱中N218圆柱滚子轴承正常、外圈磨损、滚动体故障、点蚀和压痕四种状态特征为提取对象,如图14所示。
外圈故障和滚动体故障为磨损0.2mm厚,实验中采样频率为20kHz、电机转速为1000r/min、输出扭矩为100N·m。实验故障轴承均选在输出轴位置的圆柱滚子轴承,传感器布点在输出轴轴承正上方。轴承型号是N218,类型为圆柱滚子轴承、轴承直径为125.0mm、厚度B=30.0mm、滚动体直径为18.4mm、滚子数量为17,采用MS-LE方法对轴承四种状态数据进行分析,结果如图15所示。
从图15可知:轴承的四种状态特征彼此分离,滚动体特征聚集性不强,其他三种状态特征聚集性强,特征提取效果好。说明了MS-LE方法对此特种车辆变速箱滚子轴承故障特征提取的有效性。
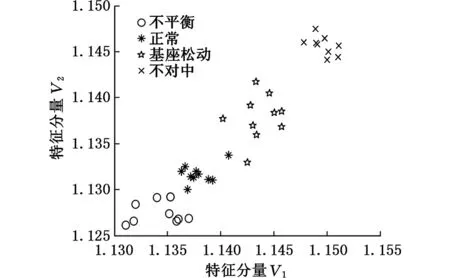
(a)XY平面映射图
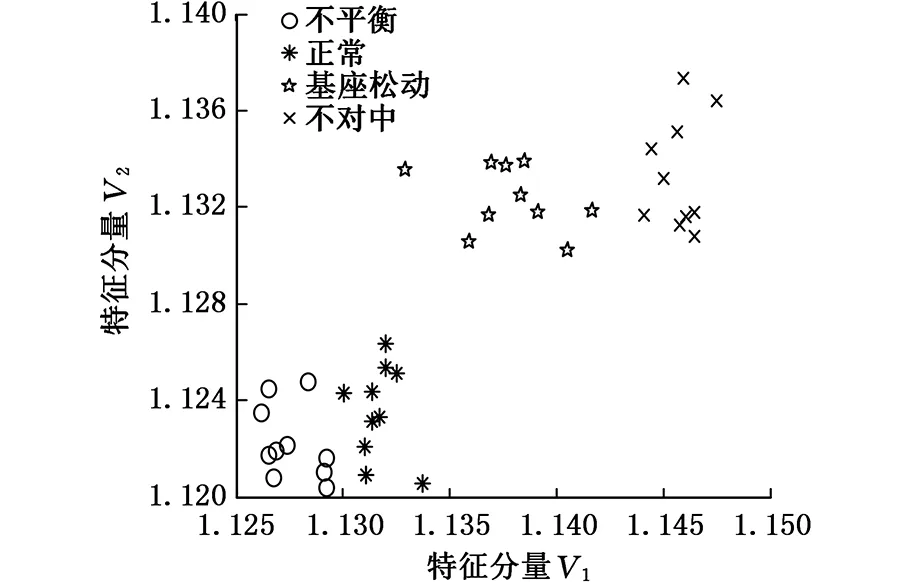
(b)XZ平面映射图

(a)外圈磨损 (b)滚动体故障(c)点蚀和压痕图14 轴承三种故障状态图

图15 MS-LE方法的轴承故障特征提取效果图
4 结论
(1)转子故障信号本身存在非线性、非平稳的特征。传统分析方法对其潜在信息的挖掘和特征的提取表现不足,采用多尺度拉普拉斯特征映射方法就可以很好地解决这个问题,尤其是对松动等非线性故障能有效地挖掘故障的信号特征。
(2)通过实验分析对比了PCA算法、LLE算法、LE算法和MS-LE方法,结果表明多尺度拉普拉斯特征映射方法对于转子系统非线性、非平稳等敏感的故障特征挖掘能力表现强劲,效果好。
[1]RandallRB.TheRelationshipbetweenSpectralCorrelationandEnvelopeAnalysisintheDiagnosticsofBearingFaultsandOtherCyclostationaryMachineSignals[J].MechanicalSystemandSignalProcessing,2002, 15(5): 945-962.
[2]OughJR.DevelopmentandAnalysisofTimeVariantDiscreteFourierTransformOrderTracking[J].MechanicalSystemandSignalProcessing, 2003, 17(6): 185-199.
[3]李晓虎, 贾民平,许飞云. 频谱分析法在齿轮故障诊断中的应用[J]. 振动、测试与诊断, 2003, 23(3): 168 -170.
LiXiaohu,JiaMinping,XuFeiyun.VirtualInstrumentsBasedRemoteEquipmentDiagnosis[J].JournalofVibration,Measurement&Diagnosis, 2003, 23(3): 168-170.
[4]SeungHS,DanielDL.TheManifoldWaysofPerception[J].Science(S0036-8075),2000,290(5500):2268-2269.
[5]RoweisS,SaulL.NonlinearDimensionalityReductionbyLocallyLinearEmbedding[J].Science(S0036-8075),2000,290(5500):2323-2326.
[6]BelkinM,NiyogiP.LaplacianEigenmapsforDimensionalityReductionandDataRepresentation[J].NeuralComputation, 2003, 15(6):1373-1396.
[7]BelkinM,NiyogiP.LaplacianEigenmapsandSpectralTechniquesforEmbeddingandClustering[J].AdvancesinNeuralInformationProcessingSystems, 2002,14(6):585-591.
[8]ZhangZhenyue,ZhaHongyuan.PrincipalMaino-fldsandNonlinearDimensionReductionviaTangentSpaceAlignment[J].SIAMJouralonScinetificComputeing,2005,26 (1):313-338.
[9]刘继伟. 基于大数据的多尺度状态监测方法及应用[D]. 北京: 华北电力大学, 2013.
[10]李鹏. 多尺度分析方法在旋转机械状态监测中的应用研究[D]. 合肥: 中国科学技术大学, 2012.
[11]张龙, 张磊, 熊国良. 基于多尺度熵和神经网络的滚动轴承故障诊断[J]. 机械设计与研究, 2014,30(5): 96-99.
ZhangLong,ZhangLei,XiongGuoliang.BasedontheMulti-scaleEntropyoftheNeuralNetworkandtheRollingBearingFaultDiagnosis[J].MechanicalDesignandResearch, 2014,30(5): 96-99.
[12]SinhaJK,LeesAW,FriswellMI.EstimatingUnbalanceandMisalignmentofaFlexibleRotatingMachinefromaSingleRun-down[J].JournalofSoundandVibration, 2004,30(9): 967-989.
[13]张靖, 闻邦椿. 两端支座松动转子系统的频率特性分析[J]. 中国机械工程, 2008, 19(1): 68-71.
ZhangJing,WenBangchun.OnBothEndsofthePedestalLoosenessFrequencyCharacteristicAnalysisofRotorSystem[J].ChinaMechanicalEngineering, 2008, 19(1): 68-71.
(编辑王艳丽)
Multi-scale Laplace Feature Mapping for Rotor Fault Feature Extraction
Wang Guangbin1Du Xiaoyang1Luo Jun1,2
1.Hunan University of Science and Technology, Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment,Xiangtan,Hunan,411201 2.Shenzhen Branch of CCCC-second Harbour Engineering Company Limited,Shenzhen,Guangdong,518067
Based on theory of multi-scale decomposition and manifold learning thought, a multi-scale Laplasse feature map algorithm for fault feature extraction was proposed. Firstly, the multi-scale wavelet packet decomposition of the rotor fault vibration signals was carried out. The optimal scale wavelet entropy of each independent frequency band signals was extracted, and the characteristic parameter matrix was constructed and the intrinsic dimension was estimated. Then the characteristic parameters of data were embedded into a low dimensional eigenspace by Laplasse feature mapping to get the most sensitive feature of faults. Lastly, the accurate identification of faults was realized by the fusion decision. Experiments show that, compared with the principal component analysis, local linear embedding and Laplacian eigenmap algorithm, rotor fault feature signal extraction of multi-scale Laplasse feature mapping method is more easily identify.
rotor system; Laplacian eigenmap; multi-scale; feature extraction
2015-08-15
国家自然科学基金资助项目(51575178,U1433118)
TP277
10.3969/j.issn.1004-132X.2016.20.017
王广斌,男,1974年生。湖南科技大学湖南省机械设备健康维护重点实验室副教授。主要研究方向为流形学习方法、信号处理和旋转机械故障诊断。发表论文40余篇。杜晓阳,男,1989年生。湖南科技大学机电工程学院硕士研究生。罗军,男。1989年生。湖南科技大学机电工程学院硕士研究生,中交第二航务工程局有限公司深圳分公司技术员。
