一种新的预测铣刀刀尖频响函数的方法

朱坚民　 何丹丹　 田丰庆　 赵全龙

上海理工大学，上海，200093



一种新的预测铣刀刀尖频响函数的方法

朱坚民 何丹丹 田丰庆 赵全龙

上海理工大学，上海，200093

为准确快速地预测铣刀刀尖点频响函数，提出一种基于逆响应耦合子结构分析(IRCSA)法辨识刀柄-刀具结合面参数的刀尖点频响函数预测方法。该方法通过建立计算刀柄末端频响函数矩阵和刀尖点频响函数矩阵的数学模型，利用逆响应耦合子结构分析法求取随频率变化的刀柄-刀具结合面参数。通过Cuckoo search算法及有限元分析确定刀尖点频响函数中对刀柄-刀具结合面复刚度矩阵变化最为敏感的固有频率，取该频率对应的结合面参数为刀柄-刀具结合面复刚度矩阵的辨识结果，由此计算出刀尖点频响函数。通过硬质合金圆柱棒、2刃铣刀和4刃铣刀进行验证，对比了所提预测方法、Cuckoo search优化算法预测的刀尖点频响函数与实测值三者之间的差异，实验结果表明该预测方法预测的刀尖点频响函数的固有频率和实测固有频率的误差在5%以内，所用时间约为Cuckoo search优化算法的1%，达到了较高的预测精度，并且更加省时、简便。

刀尖点频响函数；逆响应耦合子结构分析(IRCSA)；结合面复刚度矩阵；Cuckoo search算法；预测

0　引言

数控机床主轴系统包含主轴-刀柄、刀柄-刀具等特性较为复杂的结合面，结合面作为主轴系统的薄弱环节，其模型的准确性直接影响到主轴系统刀尖点频响函数的预测精度[1]。

国内外学者在考虑主轴系统结合面建模预测刀尖点频响函数的研究方面进行了较多的探索和尝试，主要可归纳为两大类，第一类是通过优化算法辨识结合面参数，即以主轴系统中的结合面参数为优化变量，以刀尖点频响函数(frequency response function,FRF)的实测值和理论值之间误差的最小值为目标函数，通过优化算法搜索到结合面参数的最优解。如Schmitz等[2]基于响应耦合子结构分析 (receptance coupling substructure analysis，RCSA) 法，采用集中的弹簧阻尼单元建立刀柄-刀具结合面模型，通过最小二乘法辨识结合面参数。Wang等[3]基于RCSA法，采用粒子群优化(PSO)算法辨识刀柄-刀具结合面参数。闫蓉等[4]以均匀分布的弹簧-阻尼单元模拟刀柄-刀具结合部之间的柔性连接，采用遗传算法(GA)辨识刀柄-刀具结合部的刚度和阻尼系数。Xiao等[5]建立了模拟主轴-刀柄锥部结合面的实验模型动力学方程，采用非线性最小二乘法识别出结合部参数。第二类是通过建立结合面的理论分析模型确定结合面参数。如赵万华等[6]基于经典力学和吉村允孝结合面接触刚度积分计算法，提出一种考虑刀具-夹套、夹套-刀柄以及刀柄-主轴结合部特性的主轴系统动力学建模方法。Yang等[7]基于振动理论建立了刀柄-弹性夹头-刀具三者之间无质量连续弹性层的动力学模型。Schmitz等[8]提出了基于刀柄-刀具多点结合面参数模型的刀尖点频响函数预测方法，利用胡克定理和黏性阻尼等效原理，通过ANSYS分析计算出结合面参数。陈建等[9]基于文献[8]的方法辨识了主轴-刀柄、刀柄-刀具的结合面参数，探究了主轴系统中各个结合面对主轴系统动态特性的影响规律。

上述文献中，采用优化算法辨识结合面参数的方法虽然可达到一定的辨识精度，但是需要在测试频带内进行全频带的搜索，计算量较大、寻优时间长，且参数的辨识精度依赖于优化算法的性能和搜索空间的合理设置。理论分析法虽然有助于深入了解结合面的特性，但是采用该方法进行分析计算时，需对结合面的实际结构进行简化，并对结合面模型进行假设，导致该方法的建模精度与实际情况存在一定的差异。

此外，多数文献未考虑结合面模型中力矩对位移的耦合作用以及力对转角的耦合作用，而Park等[10]认为准确预测刀尖点频响函数时需考虑主轴系统各个子结构的转动频响函数。Burns等[11]也指出基于考虑耦合作用的结合面模型所预测出的刀尖点频响函数更加准确。

针对上述问题，本文提出了一种基于逆响应耦合子结构分析(inverse receptance coupling substructure analysis，IRCSA)法快速辨识刀柄-刀具结合面参数的刀尖点频响函数预测方法。通过Cuckoo search优化算法和ANSYS仿真分析，确定对刀柄-刀具结合面参数变化最为敏感的刀尖点频响函数的固有频率，取该频率下的结合面参数为刀柄-刀具结合面复刚度矩阵的数值，并据此预测刀尖点频响函数。

1　主轴系统刀柄-刀具结合面建模

主轴系统主要包括主轴、刀柄、刀具，对于确定的主轴系统，与之配合的刀柄基座的几何尺寸是确定不变的[12]，而安装在刀柄中的刀具经常更换，因此本文将主轴和刀柄基座视为一体，仅考虑刀柄-刀具之间结合面的建模。本文采用IRCSA法辨识刀柄-刀具结合面参数，并据此预测刀尖点频响函数。IRCSA是RCSA的逆过程，RCSA法是Schmitz等[2]于2000年提出用于预测铣削系统刀尖点频响函数的方法，该方法将机床整机划分为若干个子结构，通过理论计算或实验测试确定各子结构的频响函数矩阵，然后通过位移协调方程和力平衡方程耦合各子结构，进而获得结构整体的频响函数矩阵。而IRCSA则是利用系统的频响函数矩阵反求出RCSA中除系统频响函数矩阵以外的其他未知参数矩阵的过程，与RCSA相比，其关键点在于系统频响函数矩阵的计算。

本文先将机床-主轴系统划分为刀具(子结构Ⅰ)、机床-主轴-刀柄(子结构Ⅱ)两个子结构，两个子结构之间通过弹簧阻尼单元连接，如图1所示。

图1　机床-主轴系统子结构划分示意图

图1中，K表示子结构Ⅰ和子结构Ⅱ之间的结合面复刚度矩阵。基于RCSA原理耦合子结构Ⅰ和子结构Ⅱ得

GSHT11=T11-T12a(T2a2a+GSH2b2b+K-1)-1T2a1

(1)

其中，GSHT11为刀尖点频响函数矩阵；GSH2b2b为刀柄末端的频响函数矩阵；K为未知参数矩阵，根据IRCSA得

K=(T2a1(T11-GSHT11)-1T12a-T2a2a-GSH2b2b)-1

(2)

其中，Tij为子结构Ⅰ在自由状态下的频响函数矩阵(i,j=1,2a)。K可表示为

(3)

式中，k1、c1分别为刀柄-刀具结合面受力载荷作用的平动刚度和平动阻尼；k2、c2分别为刀柄-刀具结合面受力矩作用的平动刚度和平动阻尼；k3、c3分别为刀柄-刀具结合面受力载荷作用的转动刚度和转动阻尼；k4、c4分别为刀柄-刀具结合面受力矩作用的转动刚度和转动阻尼；ω为角频率。

对于本文所研究的主轴系统，根据Maxwell互易性原理[13]，可知k2=k3，c2=c3。则K中只有k1、k2、k4、c1、c2、c4六个未知参数。

目前在结合面建模研究方面，一般将刀柄-刀具结合面简化为一个集中的弹簧阻尼单元或多个并联的均匀弹簧阻尼单元，即将刀柄-刀具结合面参数视为不随频率变化的常数。所以理论上，通过式(2)求解刀柄-刀具结合面参数时，同一个结合面参数在任意频率处的计算结果应相等。但是在实际测量与计算时，由于系统在不同频率处的频响函数幅值大小不等，在固有频率处的频响幅值较大，而在非固有频率处的频响幅值较小，一般接近于0，因此通过式(2)计算得到的刀柄-刀具结合面参数在测试频带内的数值大小不等。为确定刀柄-刀具结合面参数，本文首先通过比PSO算法[3]、GA算法[4]搜索性能更好的Cuckoo search算法辨识出刀柄-刀具结合面参数，确定结合面复刚度矩阵，然后通过改变结合面复刚度矩阵的放大倍数，利用ANSYS仿真分析出对刀柄-刀具结合面参数变化最为敏感的刀尖点频响函数的固有频率，结合式(2)，取该频率下的结合面参数为K的取值。

为准确求解式(2)，还需确定GSHT11、GSH2b2b以及Tij(i,j=1,2a)，具体推导见第2节。

2　各子结构频响函数矩阵的计算

式(1)、式(2)中，Tij、GSHT11依次表示为

(4)

(5)

式中，Hij、Lij、Nij和Pij依次为子结构Ⅰ在j点激励下i点获得响应的位移/力、位移/力矩、转角/力以及转角/力矩频响函数(i,j=1,2a)；Fj、Mj分别为子结构Ⅰ在j点处所受到的外力和外力矩；Xi、θi分别为子结构Ⅰ在外力和外力矩的作用下i点处的平动位移和转角。HSHT11、LSHT11、NSHT11和PSHT11依次表示刀尖点的位移/力、位移/力矩、转角/力以及转角/力矩频响函数，其中HSHT11也可称为刀尖点原点频响函数，以下简称为刀尖点频响函数。

图1中，刀具(子结构Ⅰ)可简化为EB梁模型，其频响函数Tij(i,j=1,2a)的计算可参考文献[13]。

式(2)中，GSH2b2b和GSHT11包含转动频响函数，因转角不易测量，故与转动自由度相关的频响函数难以得到。目前，一般采用间接法求解转动频响函数，如一阶、二阶有限差分法[14]以及多段EB梁优化法[15]。有限差分法的计算精度依赖于所设激励点之间的距离大小，目前没有确定该距离的理论依据；多段EB梁优化法需要优化的待定参数较多，方法相对繁琐。为此，本文建立了计算GSH2b2b和GSHT11的数学模型，分别进行一次实验测量，通过求解方程组分别得到GSH2b2b和GSHT11。本节以求解刀柄末端的频响函数矩阵GSH2b2b为例进行说明。

将机床-主轴-刀柄(子结构Ⅱ)进一步划分为机床-主轴-刀柄基座和剩余刀柄两个子结构，如图2所示。

(a)机床-主轴-刀柄的结构示意图

(b)机床-主轴-刀柄基座和剩余刀柄子结构的结构示意图图2　刀柄末端频响函数矩阵GSH2b2b的计算模型

图2中，XS2、θS2分别表示在外力和外力矩的作用下刀柄基座末端处的平动位移和转角。XH2、θH2分别表示在外力和外力矩的作用下剩余刀柄子结构在点2处的平动位移和转角。XH1、θH1分别表示在外力和外力矩的作用下剩余刀柄子结构在点1处的平动位移和转角。XSH1、θSH1分别表示在外力和外力矩的作用下机床-主轴-刀柄在点1处的平动位移和转角。XSH2、θSH2分别表示在外力和外力矩的作用下机床-主轴-刀柄在点2处的平动位移和转角。

根据图2中两个子结构之间的位移协调方程和力平衡方程，可得

(6)

(7)

结合式(6)、式(7)，消去FH2和MH2。由于FH2和MH2的展开式较为复杂，故需对FH2和MH2进行简化。由式(6)可知，FH2和MH2可表示成FSH1、FSH2、MSH2的函数，即

(8)

联立式(6)、式(8)，根据等式两边FSH2、MSH2前的系数对应项相等，可得

(9)

联立式(7)、式(8)，经过整理得

(10)

式(10)中，HSHX1F1、HSHX1F2、HSHX2F1、HSHX2F2可通过实验测试得到。

根据互易性原理，式(10)中，HSHX2F1=HSHX1F2。再根据RCSA原理，将剩余刀柄子结构划分成多段EB梁，如图3所示。根据文献[13]计算各子结构在自由状态下两端的频响函数矩阵，经过耦合得到

会上，牟嘉云在致辞中说：“2018年，云图控股在国际国内经济形势如此严峻的情况下，依然取得了骄人的业绩。”她表示，前三个季度云图控股的复合肥、联碱、品种盐、磷酸一铵等产品销量业绩突出，实现销售收入59.3亿元，归属上市公司股东的净利润比去年同期增长68.23%。她说：“预计到2018年可实现销售收入80亿元，上交税费3.3亿元。”

图3　剩余刀柄子结构划分示意图

GSH2b2b=DH2b2b-DH2b5a(DH5a5a+S5b5b)-1DH5a2b

(11)

式(11)中，GSH2b2b可写成

(12)

DH2b2b、DH2b5a分别表示为图2b中剩余刀柄子结构自由状态下在点1处的原点频响函数矩阵和跨点频响函数矩阵，可分别写成

(13)

(14)

DH5a5a、DH5a2b分别表示图2b中剩余刀柄子结构自由状态下在点2处的原点频响函数矩阵和跨点频响函数矩阵，根据互易性原理，DH2b5a=DH5a2b，DH5a5a可写成

(15)

S5b5b为刀柄基座的频响函数矩阵，可写成

(16)

联立式(9)、式(10)，可求得S5b5b，通过RCSA原理可求得DH2b2b、DH2b5a、DH5a5a、DH5a2b，代入式(11)可得GSH2b2b。同理可得刀尖点的频响函数矩阵GSHT11。

3　主轴系统刀柄-刀具结合面参数辨识

根据式(2)以及第2节中计算得到的Tij(i,j=1,2a)、GSH2b2b和GSHT11，可得主轴系统刀柄-刀具结合面复刚度矩阵K。由第1节分析可知，为确定K的取值，应分析出对刀柄-刀具结合面复刚度矩阵变化最敏感的刀尖点频响函数的固有频率，具体步骤如下。

(1)采用优化算法辨识刀柄-刀具结合面参数。为提高结合面参数的辨识效率和精度，获得较为准确的刀柄-刀具结合面参数，本文以主轴系统的实测刀尖点频响函数HSHTm11和理论计算得到的刀尖点频响函数HSHTt11之间差值的Frobenius范数为目标函数，以K中的未知参数k1、k2、k4、c1、c2、c4为优化变量，通过Cuckoo search算法辨识结合面参数。

E=min‖HSHTt11-HSHTm11‖

(17)

Cuckoo search算法[16]是英国剑桥大学学者杨新社等2009年提出的一种新兴的启发式智能优化算法，该算法简单易行，需要确定的参数较少，在解决特殊问题时无需重新匹配大量参数，相对于GA、PSO等经典的启发式智能优化算法，该算法在解决很多优化问题上更胜一筹[17]。为说明Cuckoo search算法比目前文献[3]中的PSO算法、文献[4]中的GA算法在辨识刀柄-刀具结合面参数方面更为有效，本文在第4节中对比了基于Cuckoo search、PSO以及GA三种算法预测的刀尖点频响函数的前四阶固有频率。

(2)基于IRCSA辨识结合面复刚度矩阵。根据Cuckoo search算法辨识的结合面参数，在ANSYS中采用matrix27单元模拟刀柄-刀具结合面复刚度矩阵，通过改变结合面复刚度矩阵的倍数，观察主轴系统刀尖点频响函数的变化，结合式(2)，确定变化最显著的固有频率对应的结合面参数为K的取值。

4　实验验证

为验证本文方法的有效性，基于VMC850E立式加工中心，先以一把硬质合金圆柱棒为例，对上述理论进行验证，再将该方法推广到常用的2刃铣刀和4刃铣刀，刀具参数如表1所示，实验和计算步骤如下。

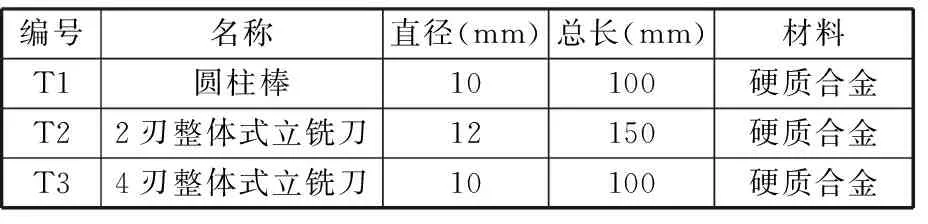
表1　实验刀具的参数

图4　计算GSH2b2b搭建的实验平台

图5　计算GSHT11搭建的实验平台

(1)通过理论计算得到K。按照图4搭建实验平台，将BT40 ER32-100L型刀柄安装在主轴中，将两个BK 4525B三向加速度传感器安装在刀柄的相应位置，利用Kistler 9724A激振力锤分别锤击图4中的点A、点B，通过LMS SCADAS Mobile数据采集系统同步采集加速度信号和激振力信号，配合使用LMS Test Lab软件对每个点分别进行5次测量取平均值，分别得到HSHX1F1、HSHX2F1、HSHX2F2。根据式(9)、式(10)计算得到S5b5b。S5b5b是刀柄基座处的频响函数矩阵，对于确定的主轴系统，与之配合的刀柄基座的尺寸是确定不变的，因此可将S5b5b视为确定不变的常数矩阵，将其代入式(11)计算得到GSH2b2b。同理按照图5的安装，使用激振力锤分别锤击点C、点D，按照以上步骤可计算得到GSHT11，最后根据式(2)可得到刀柄-刀具结合面复刚度矩阵K，通过第1节分析可知，K中各个参数随频率变化，在频率范围内的数值大小不等。

(2)采用优化算法辨识K值。根据第3节的原理，为说明Cuckoo search算法的有效性，本文对比了基于Cuckoo search、PSO以及GA三种优化算法预测的刀尖点频响函数的前4阶固有频率，如表2所示。

表2　三种算法预测的刀尖点频响函数和实测刀尖点频响函数固有频率对比

由表2可知，总体来说，基于三种优化算法预测的刀尖点频响函数和实测值的差别较小，误差均在4%之内。但Cuckoo search算法预测的刀尖点频响函数的前四阶固有频率和实测值的误差，除了前二阶的误差和其他两种算法相同外，第3阶、第4阶的误差要低于另外两种算法的预测结果，并且搜索耗时更少。因此Cuckoo search算法在辨识刀柄-刀具结合面参数方面要比文献[3]中的PSO算法和文献[4]中的GA算法更加有效。

(3)建立刀柄-刀具的有限元模型。在SolidWorks中建立刀柄-刀具的实体模型，忽略较小的倒角、圆弧以及螺纹，简化实体模型，导入HyperMesh中，设置单元为solid186，并进行网格划分，划分得到283 388个节点，98 379个单元，如图6所示。施加约束条件，将刀柄与主轴接触的一面设置成只保留轴向转动自由度，约束其他5个自由度，拉钉和刀柄的接触面、圆螺母和弹性夹头的接触面均设为刚性连接。弹性夹头-刀具结合面采用matrix27单元进行模拟，然后导入ANSYS中，在刀尖点处施加单位力载荷，进行谐响应分析，得到刀尖点的频响函数(FRF)。通过改变结合面复刚度矩阵的放大倍数，得到不同放大倍数的结合面复刚度矩阵预测的刀尖点频响函数，如图7所示。

图6　刀柄-刀具的有限元模型

图7　刀柄-刀具结合面复刚度矩阵对刀尖点频响函数的影响

由图7可知，刀柄-刀具结合面复刚度矩阵影响刀尖点频响函数的第3阶固有频率。因此，取刀尖点频响函数第3阶固有频率下对应的结合面参数为K的取值，如表3所示。将该值代入式(1)中计算得到刀尖点频响函数的理论值，并和Cuckoo search算法预测的刀尖点频响函数以及实测值进行对比，如图8所示，三者的前四阶固有频率的对比如表4所示。

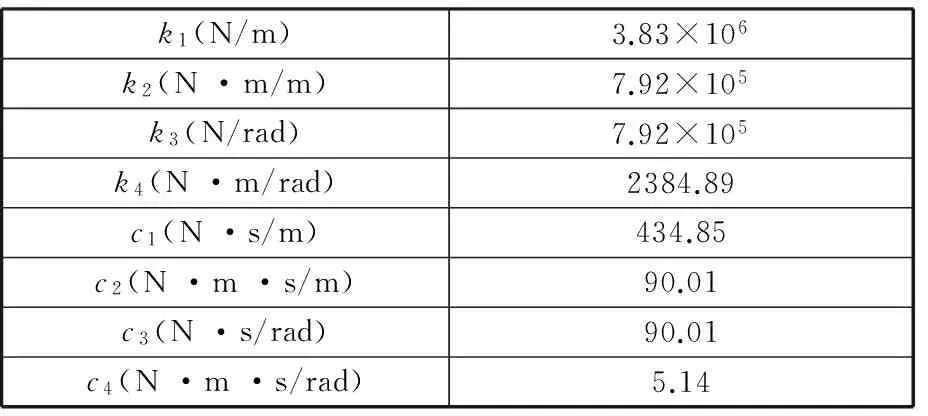
表3　本文方法辨识的刀柄-刀具结合面参数

由图8和表4可知，基于本文方法、Cuckoo search算法预测的刀尖点频响函数与实测值的前四阶固有频率的误差均在4%之内。对于第1阶、第2阶固有频率的预测，两种方法预测的精度相同。对于第3阶固有频率的预测，相比于Cuckoo search算法的预测值，本文预测的结果更加接近实测值。对于第4阶固有频率的预测，本文方法的预测精度稍低于Cuckoo search算法，但是由于第4阶固有频率实测值的幅值较小，因此可忽略其影响。此外，通过本文方法预测刀尖点频响函数耗时仅为21.3 s，而通过Cuckoo search算法预测刀尖点频响函数则需2089.72 s，本文方法耗时约为Cuckoo search算法的1.02%。其原因在于，采用Cuckoo search算法辨识刀柄-刀具结合面参数时，需在测试频带内进行全频带的搜索，而本文方法在分析出对刀柄-刀具结合面参数变化最敏感的刀尖点频响函数的固有频率之后，只需取对应频率下的结合面参数作为K的取值，然后直接计算刀尖点频响函数。通过以上分析可知，在预测刀尖点频响函数方面，本文方法比Cuckoo search算法更加省时，且达到了较高的预测精度。

图8　基于Cuckoo search算法、本文方法预测的铣刀刀尖点频响函数和实测值的对比

模态阶次实测值(Hz)Cuckoosearch算法本文方法预测值(Hz)误差(%)预测值(Hz)误差(%)11651603.031603.0324354320.694320.6938588640.708570.124114311571.2211702.36耗时2089.72s21.3s

为验证本文方法的普适性，采用常用的2刃铣刀和4刃铣刀分别进行验证。其中铣刀子结构按照下式采用等效质量法[18]等效为两段均质EB梁：

(18)

式中，M、ρ、ds、ls、lf依次为铣刀的质量、铣刀的密度、铣刀的刀杆直径、铣刀的刀杆长度以及铣刀的刀齿长度。

按照上述步骤，得到了基于本文方法、Cuckoo search算法预测的2刃铣刀刀尖点频响函数以及实测值，如图9所示。基于两种方法辨识的结合面复刚度矩阵如表5所示。基于本文方法、Cuckoo search算法预测的2刃铣刀刀尖点频响函数以及实测值的前3阶固有频率的对比如表6所示。

图9　基于Cuckoo search算法、本文方法预测的2刃铣刀刀尖点频响函数和实测值的对比

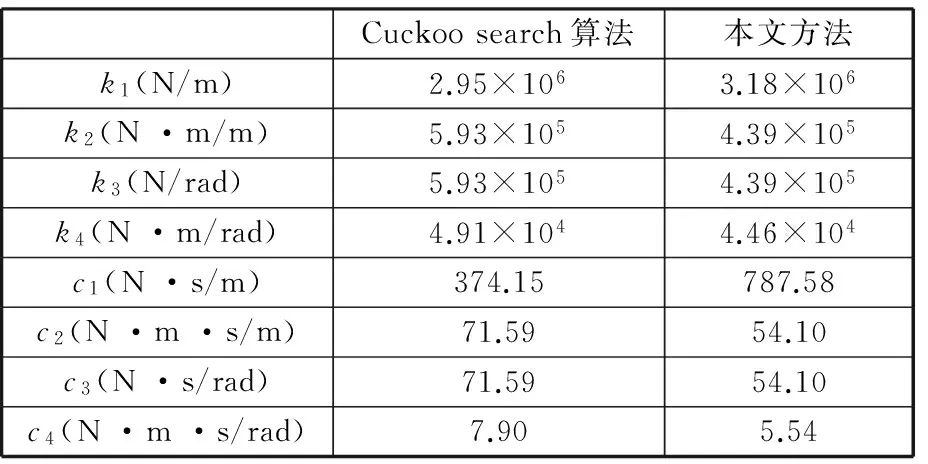
Cuckoosearch算法本文方法k1(N/m)2.95×1063.18×106k2(N·m/m)5.93×1054.39×105k3(N/rad)5.93×1054.39×105k4(N·m/rad)4.91×1044.46×104c1(N·s/m)374.15787.58c2(N·m·s/m)71.5954.10c3(N·s/rad)71.5954.10c4(N·m·s/rad)7.905.54

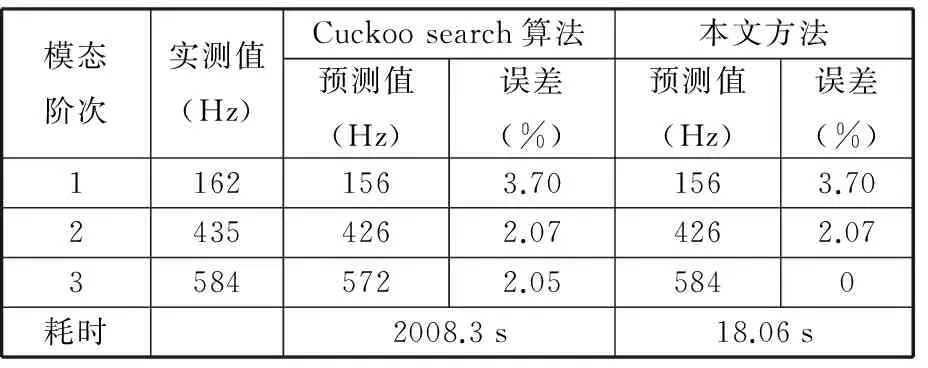
表6　基于Cuckoo search算法、本文方法预测的2刃铣刀刀尖点频响函数和实测值的固有频率对比

由图9和表6可知，基于本文方法、Cuckoosearch算法预测的刀尖点频响函数与实测值的前3阶固有频率的误差均在4%之内。对于第1阶、第3阶固有频率的预测，两种方法预测的精度相同，但是预测的幅值和实测幅值之间的误差均较大，其原因可能在于测试过程中产生了测量误差，不过两种方法预测的固有频率和实测值的差别较小。对于第3阶固有频率的预测，相比于Cuckoosearch算法的预测值，本文方法的预测值和实测值之间的误差较小。此外，通过本文方法预测刀尖点频响函数耗时仅为18.06s，而通过Cuckoosearch算法预测刀尖点频响函数则需2008.3s，本文方法耗时约为Cuckoosearch算法的0.90%，由此可见，在预测刀尖点频响函数方面，本文方法比Cuckoosearch算法更加省时，且达到了较高的预测精度。

同理，基于上述理论对4刃铣刀的刀尖点频响函数进行了预测，表7所示为基于本文方法、Cuckoosearch算法预测的4刃铣刀刀尖点频响函数以及实测值的前5阶固有频率。

表7基于Cuckoo search算法、本文方法预测的4刃铣刀刀尖点频响函数和实测值的固有频率对比

模态阶次实测值(Hz)Cuckoosearch算法本文方法预测值(Hz)误差(%)预测值(Hz)误差(%)11551560.651560.6524374321.144321.1439569223.569124.604114511853.4911792.975135013450.3713351.11耗时2193.3s23.6s

由表7可以看出，基于本文方法、Cuckoo search算法预测的刀尖点频响函数与实测值的前五阶固有频率的误差均在5%之内。对于第1阶、第2阶固有频率的预测，两种方法的预测精度相同。对于第3阶固有频率的预测，相比于Cuckoo search算法的预测值，本文方法的预测值和实测值之间的误差稍大，但是不超过5%，与目前预测刀尖点频响函数的方法[6-7,15,18]相比，该误差并不大。对于第4阶、第5阶固有频率的预测，本文方法预测的结果和实测值之间的误差较小。此外，通过本文方法预测刀尖点频响函数耗时仅为23.6 s，而通过Cuckoo search算法预测刀尖点频响函数则需2193.3 s，本文方法耗时约为Cuckoo search算法的1.08%，由此可见，在预测刀尖点频响函数方面，本文方法比Cuckoo search算法更加省时，且达到了较高的精度。

综上所述，本文提出的基于IRCSA快速辨识刀柄-刀具结合面参数的刀尖点频响函数预测方法是正确的、有效的，并且达到了较高的预测精度。

5　结论

(1)提出了一种快速辨识刀柄-刀具结合面参数的刀尖点频响函数预测方法。该方法将机床-主轴系统划分为机床-主轴-刀柄和刀具两个子结构，通过弹簧阻尼单元连接两个子结构，基于IRCSA快速准确地辨识刀柄-刀具结合面参数，进而预测出刀尖点频响函数。

(2)建立了求解刀柄末端频响函数矩阵和刀尖点频响函数矩阵的数学模型，分别进行一次实验测量，通过求解方程组得到刀柄末端的频响函数矩阵和刀尖点频响函数矩阵，进而计算出测试频带内的刀柄-刀具结合面参数随频率变化的数值。基于Cuckoo search算法和ANSYS仿真分析得到对刀柄-刀具结合面参数变化最敏感的刀尖点频响函数的固有频率，并取对应频率下的结合面参数为刀柄-刀具结合面复刚度矩阵的数值，避免了优化算法在测试频带内进行全面搜索的过程。

(3)以硬质合金圆柱棒为例，对比了Cuckoo search、PSO以及GA三种优化算法对刀尖点频响函数的预测精度，结果表明Cuckoo search算法更加有效；在此基础上，以硬质合金圆柱棒、2刃铣刀以及4刃铣刀为试验对象，对比了基于本文方法、Cuckoo search算法预测的刀尖点频响函数与实测值之间的差异，结果表明，本文方法比Cuckoo search算法更加省时，并且达到了较高的预测精度。因此本文方法是一种计算刀柄-刀具结合面参数快速而有效的方法，并为辨识同类结合面参数提供了参考。

[1]汪博, 孙伟, 太兴宇, 等. 主轴系统结合面对主轴系统动力学特性的影响分析[J]. 振动与冲击, 2011, 30(10): 231-235.

Wang Bo, Sun Wei, Tai Xingyu, et al. Effect of Interfaces on Dynamic Characteristics of a Spindle System[J]. Journal of Vibration and Shock, 2011, 30(10): 231-235.

[2]Schmitz T L, Donaldson R. Predicting High-speed Machining Dynamics by Substructure Analysis[J]. Annals of the CIRP, 2000, 49(1): 303-308.

[3]Wang Erhua, Wu Bo, Hu Youmin, et al. Dynamic Parameter Identification of Tool-spindle Interface Based on RCSA and Particle Swarm Optimization[J]. Shock and Vibration, 2013, 20(1): 69-78.

[4]闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报(自然科学版), 2013, 41(4): 1-5.

Yan Rong, Cai Feifei, Peng Fangyu, et al. Predicting Frequency Response Function for Tool Point of Milling Cutters Using Receptance Coupling[J]. Huazhong University of Science & Technology (Natural Science Edition), 2013, 41(4): 1-5.

[5]Xiao Weiwei, Mao Kuanmin, Zhu Ming, et al. Modelling the Spindle-holder Taper Joint in Machine Tools: a Tapered Zero-thickness Finite Element Method[J]. Journal of Sound and Vibration, 2014, 333(22): 5836-5850.

[6]赵万华, 杜超, 张俊, 等. 主轴转子系统动力学解析建模方法[J]. 机械工程学报, 2013, 49(6): 44-51.

Zhao Wanhua, Du Chao, Zhang Jun, et al. Analytical Modeling Method of Dynamics for the Spindle Rotor System[J]. Journal of Mechanical Engineering, 2013, 49(6): 44-51.

[7]Yang Yun, Wan Min, Ma Yingchao. An Improved Method for Tool Point Dynamics Analysis Using a Bi-distributed Joint Interface Model[J]. International Journal of Mechanical Sciences, 2016, 105: 239-252.

[8]Schmitz T L, Powell K, Won D, et al. Shrink Fit Tool Holder Connection Stiffness/damping Modeling for Frequency Response Prediction in Milling[J]. International Journal of Machine Tools & Manufacture. 2007, 47(9): 1368-1380.

[9]陈建, 田良, 商宏谟, 等. 结合部对HSK主轴系统动态特性的影响[J]. 中国机械工程, 2015, 26(9): 1161-1166.

Chen Jian, Tian Liang, Shang Hongmo, et al. Effect of Joint Part on HSK Spindle System Dynamic Performance[J]. China Mechanical Engineering, 2015, 26(9): 1161-1166.

[10]Park S S, Altintas Y, Movahhedy M. ReceptanceCoupling for End Mills[J]. International Journal of Machine Tools & Manufacture, 2003, 43(9): 889-896.

[11]Burns T J, Schmitz T L. A Study of Linear Joint and Tool Models in Spindle-holder-tool Receptance Coupling[C]//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Long Beach, California， USA: American Society of Mechanical Engineers, 2005: 947-954.

[12]张扬广. 立铣刀几何参数对铣削系统动态特性影响规律的研究[D]. 济南: 山东大学, 2013.

[13]Bishop R E D, Johnson D C. The Mechanics of Vibration[M]. New York: Cambridge University Press, 1979.

[14]Duarte M L M, Ewins D J. Rotational Degrees of Freedom for Structural Coupling Analysis via Finite-difference Technique with Residual Compensation[J]. Mechanical Systems and Signal Processing, 2000, 14(2): 205-227.

[15]李孝茹, 朱坚民, 张统超，等. 基于RCSA与GA的铣刀刀尖点频响函数预测[J]. 计算机集成制造系统, 2016, 22(1): 272-280.Li Xiaoru, Zhu Jianmin, Zhang Tongchao, et al. Frequency Response Prediction of Milling Tool Tip Point Based on RCSA and GA[J]. Computer Integrated Manufacturing Systems, 2016, 22(1): 272-280.

[16]Yang X S, Deb S. Cuckoo Search via Lévy Flights[C]//Proceedings of World Congress on Nature & Biologically Inspired Computing. Coimbatore, 2009: 210-214.

[17]赵玉新, (英)杨新社, 刘利强. 新兴元启发式优化算法[M]. 北京: 科学出版社, 2013.

[18]朱坚民, 王健, 张统超. 一种改进的基于响应耦合子结构法的刀尖点频响函数预测方法[J]. 中国机械工程, 2015, 26(3): 285-292.Zhu Jianmin, Wang Jian, Zhang Tongchao, et al. An Improved Tool Point Frequency Response Function Prediction Method Dased on RCSA[J]. China Mechanical Engineering. 2015, 26(3): 285-292.

(编辑王旻玥)

A New Prediction Method of Tool Point Frequency Response Function for Milling Cutters

Zhu JianminHe DandanTian FengqingZhao Quanlong

University of Shanghai for Science and Technology,Shanghai,200093

To predict tool point frequency response function of milling cutters accurately and rapidly, a new tool point frequency response function prediction method was proposed, which was based on IRCSA to identify joint parameters of holder-tool. Firstly, the joint parameters of holder-tool changing with the frequency were obtained by calculating frequency response function matrixes of holder end and tool point based on the mathematical models, and applying IRCSA. Secondly, the natural frequency of tool point frequency response function was determined, which was sensitive to variations of the complex stiffness matrixes of holder-tool joints by Cuckoo search algorithm and finite element analysis. At last, the joint parameters under the determined frequency were taken as the result of the complex stiffness matrix, which was used to predict the tool point frequency response function. To confirm the presented theory, a carbide cylindrical rod, 2 fluted milling cutter and 4 fluted milling cutter were taken as examples, and the predicted tool point frequency response functions based on the new method and Cuckoo search algorithm of them were compared with measured ones. It is experimentally demonstrated that the new method has high prediction precision and is time-saving, the errors between the natural frequencies of the predicted tool point frequency response functions based on the new method and measured ones are within 5%, and time the new method used is about 1% of the Cuckoo search algorithm used.

tool point frequency response function; inverse receptance coupling substructure analysis(IRCSA); complex stiffness matrix of holder-tool joint; Cuckoo search algorithm; prediction

2016-06-06

国家自然科学基金资助项目(50975179)；上海市教委科研创新项目(11ZZ136)；上海市科委科研计划资助项目(12DZ2252300)

TH113

10.3969/j.issn.1004-132X.2016.20.013

朱坚民，男，1968年生。上海理工大学机械工程学院教授、博士研究生导师。主要研究方向为精密测试技术、机电系统的智能测控。何丹丹，女，1992年生。上海理工大学机械工程学院硕士研究生。田丰庆，男，1982年生。上海理工大学机械工程学院博士研究生。赵全龙，男，1989年生。上海理工大学机械工程学院硕士研究生。